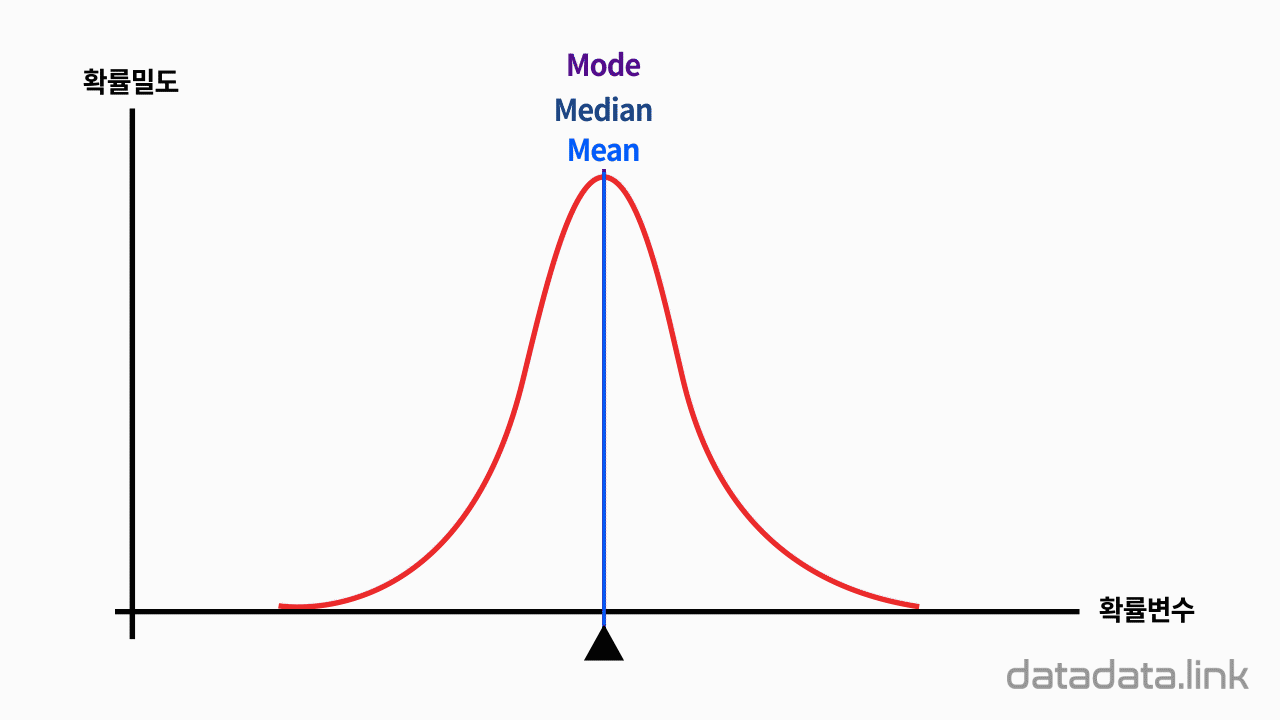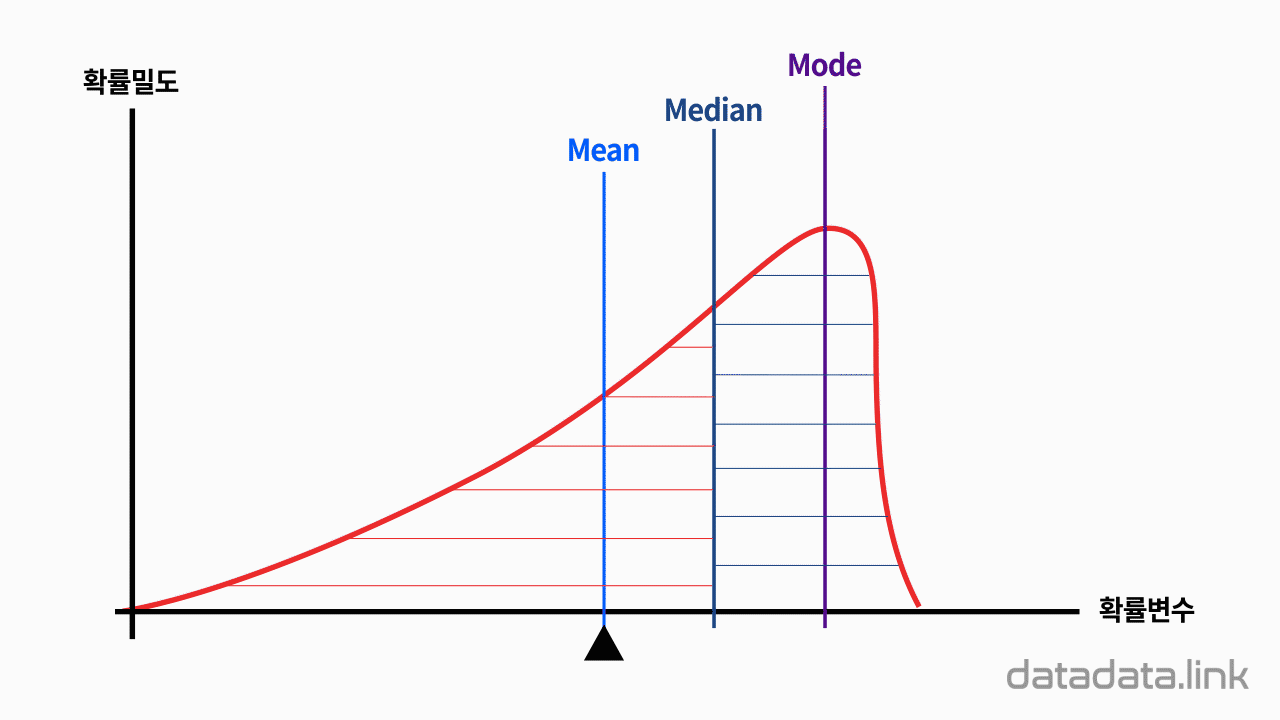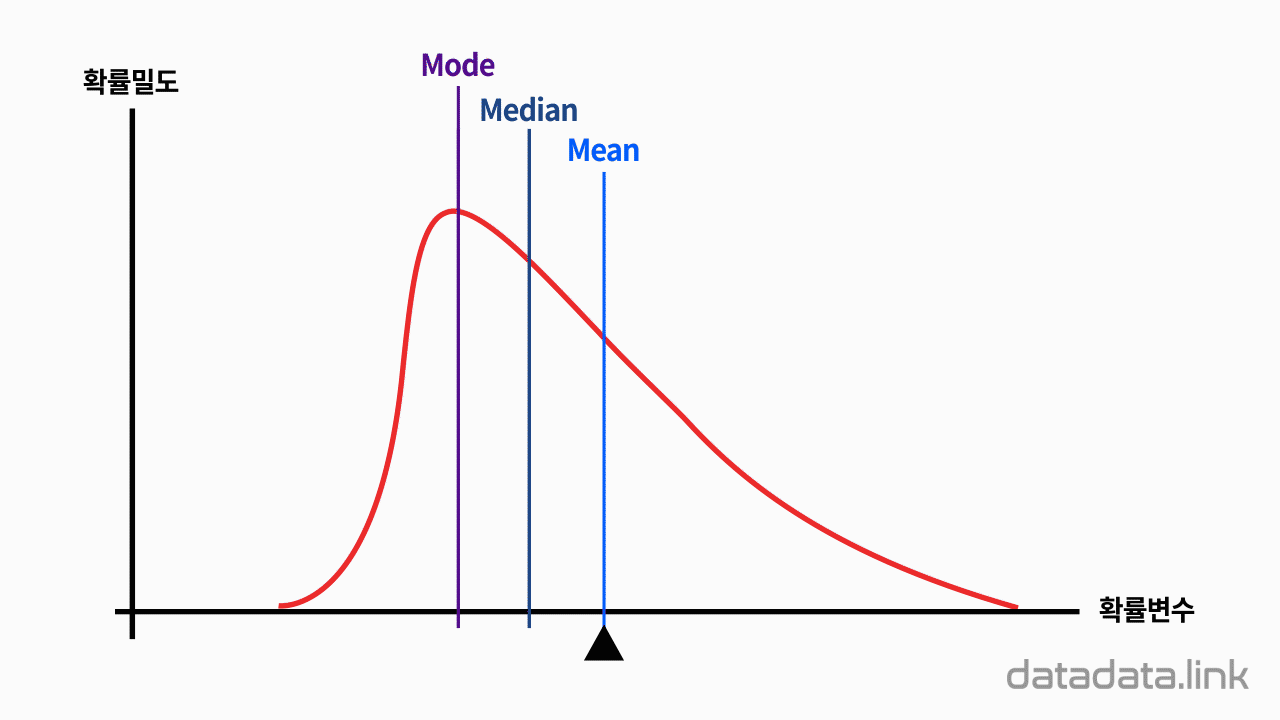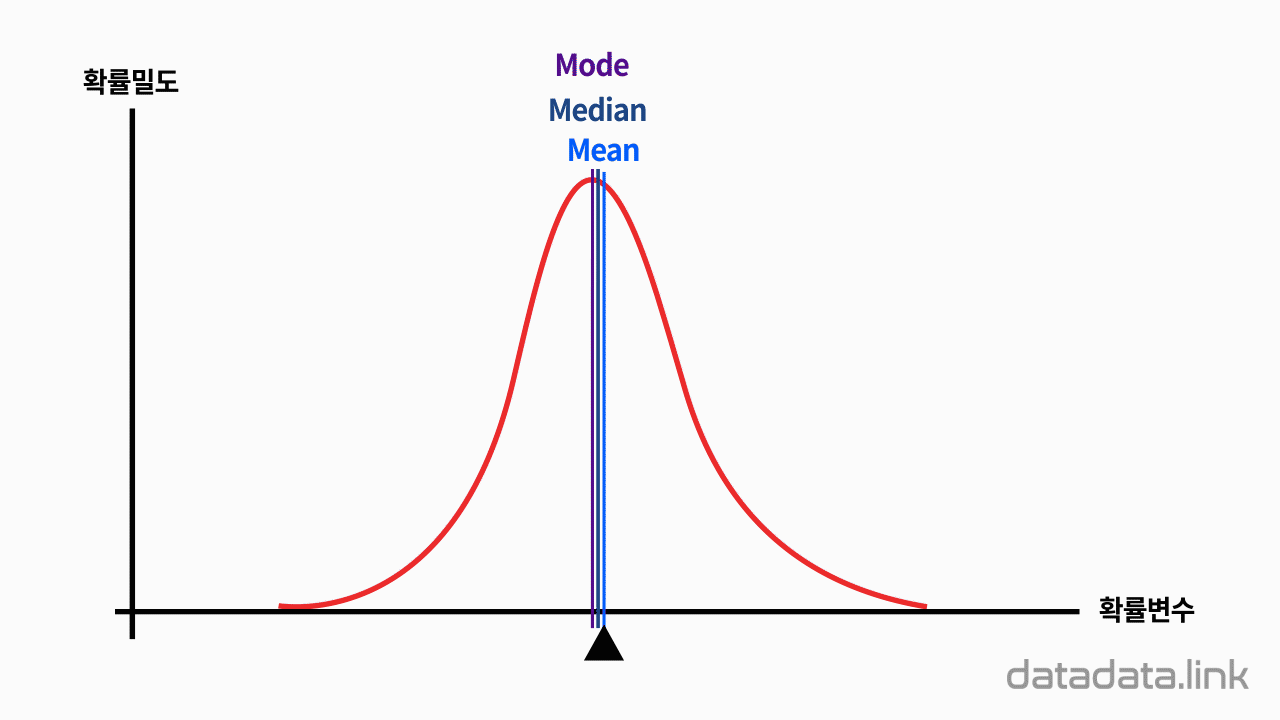
평균과 표준편차를 한 번에 비교하려면
변동계수로 비교할 수 있습니다.
변동계수(coefficient of variation, CV)는 표준편차를 산술평균을 기준으로 표준화(standardization)한 것으로, 표준편차를 산술평균으로 나눈 값입니다.
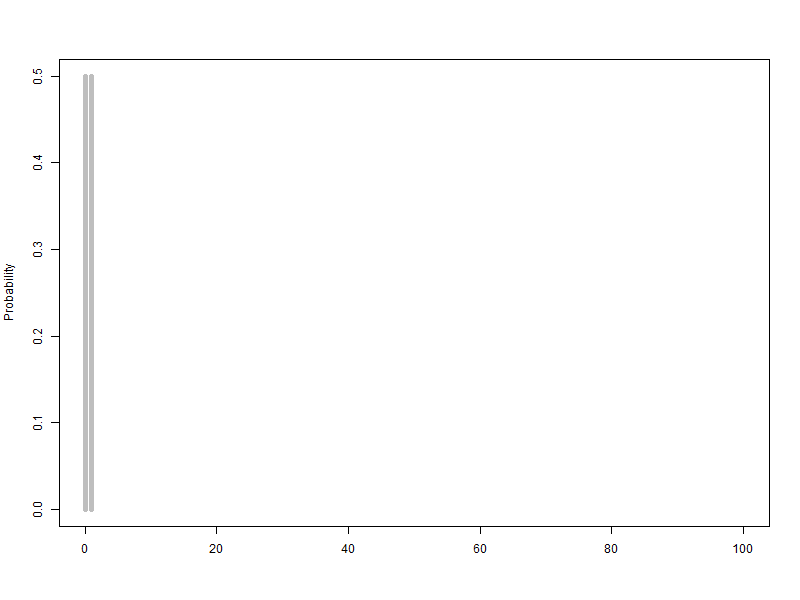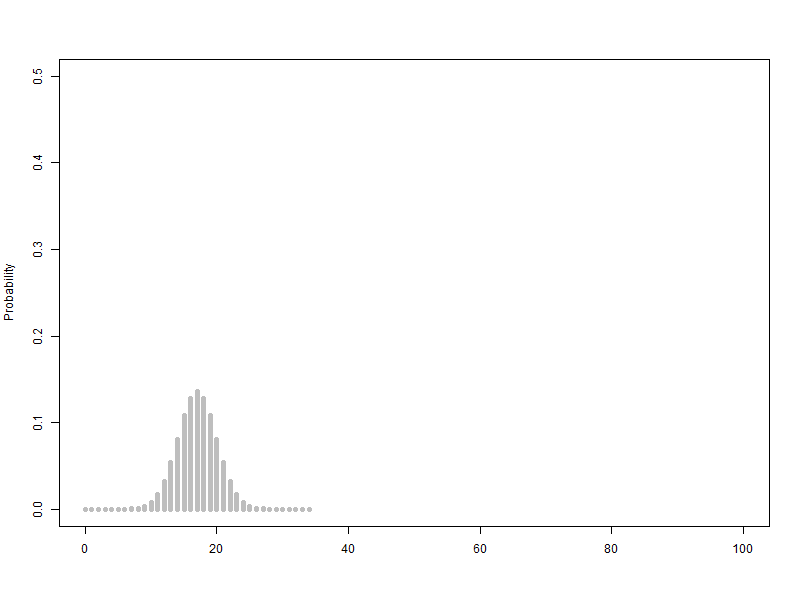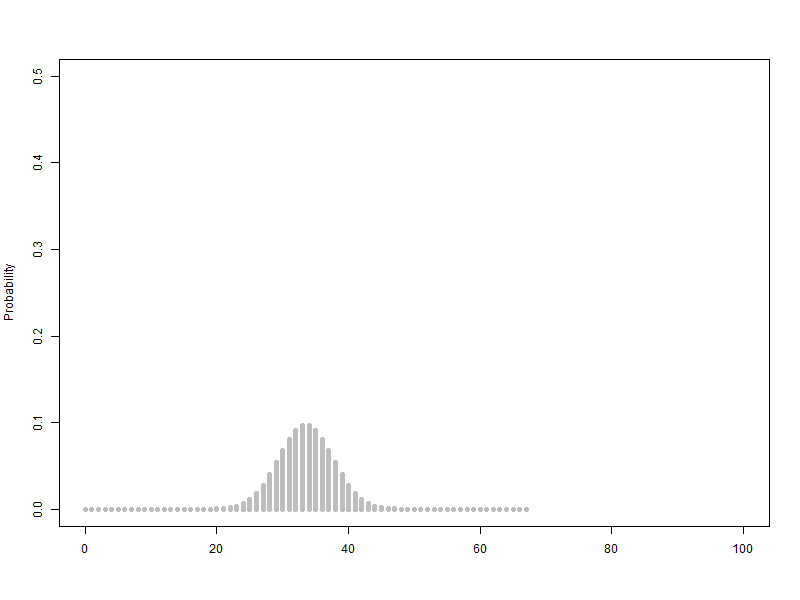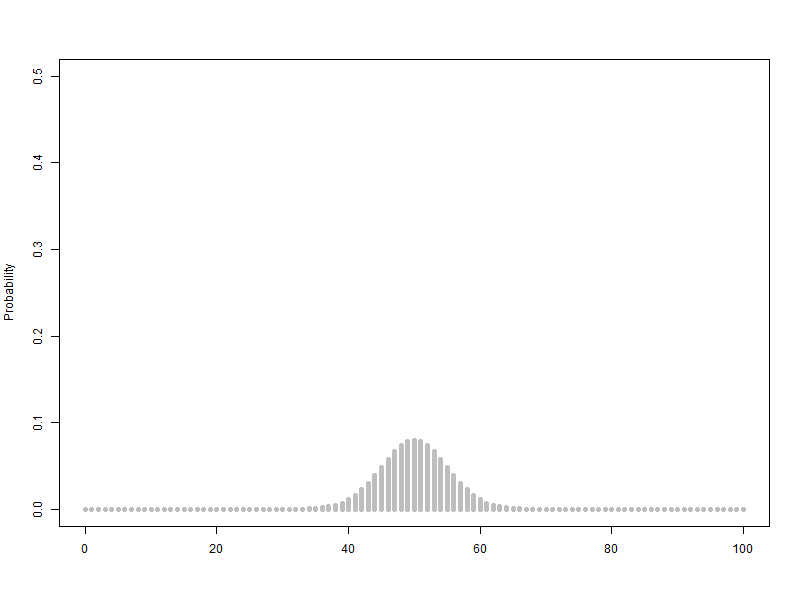
애니메이션을 보면 A와 B의 평균과 표준편차가 각각 다릅니다.
B의 평균이 A의 평균과 같아지도록 늘린 비율만큼, 표준편차를 늘려주면, A와 B의 평균이 같다는 조건 하에서의 상대적인 표준편차를 비교해볼 수 있습니다.
이러한 상대적인 표준편차를 변동계수라고 합니다.
예를 들어, 한국과 미국의 제품 가격을 비교한다고 할 때, 한국과 미국의 다른 화폐 기준으로 인해, 한국에서 1,000원, 2,000원, 3,000원인 제품이 미국에서는 1, 2, 3달러일 수 있습니다.
평균과 표준편차를 구해보면, 한국에서는 평균 2,000원, 표준편차 816원이고, 미국에서는 평균 2달러, 표준편차 0.816달러입니다.
이와 같이 자연현상과 사회현상에서 평균이 높으면 표준편차도 높아지는 경향이 있습니다.
위의 예에서 변동계수를 구하면, 둘다 0.4로 동일합니다.
같은 단위를 가지는 표준편차를 평균으로 나누면, 단위가 사라지고 표준화된 수치를 비교할 수 있기 때문에 단위에 대한 고려를 안해도 되는 이로움이 있습니다.