코로나 백신의 효과를 시험하기 위해서는 코로나백신을 접종한 사람들과 그렇지 않은 사람들을 비교하는 방법을 사용합니다.

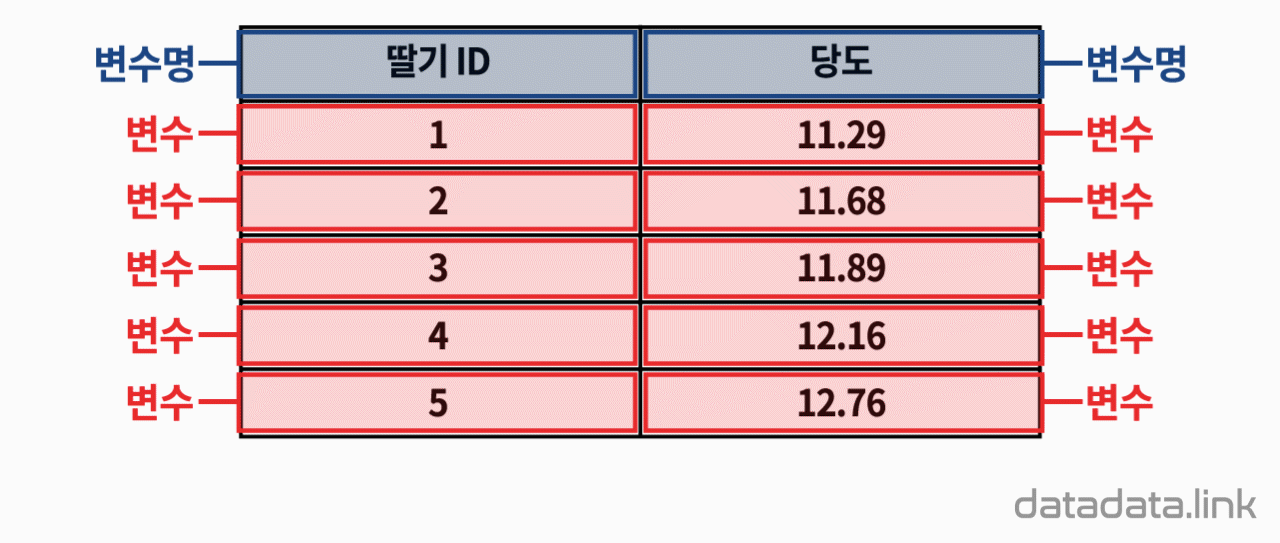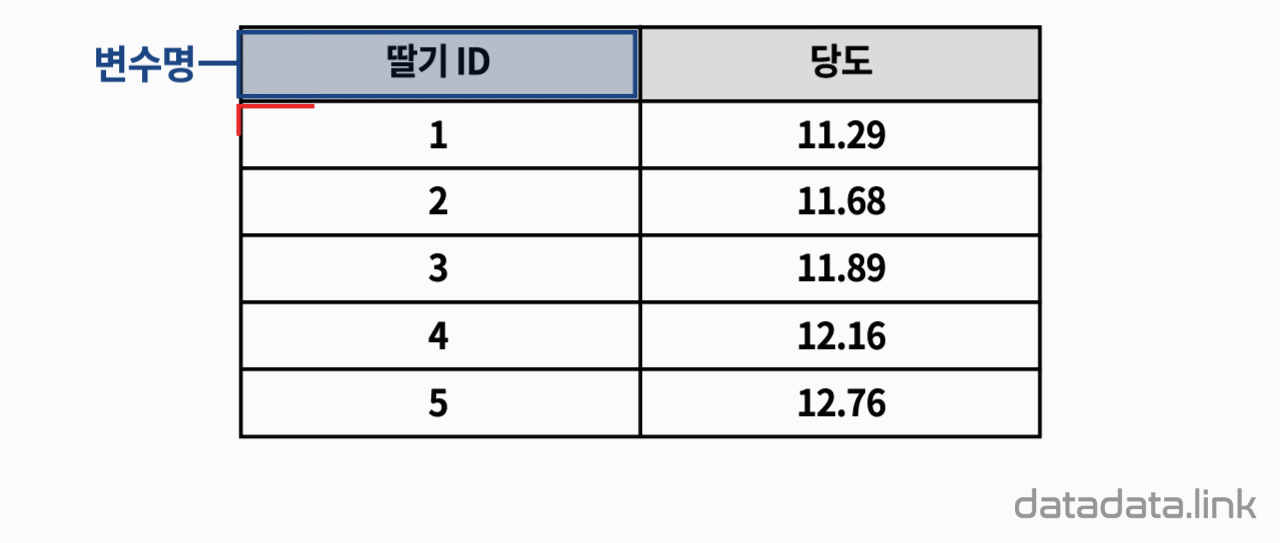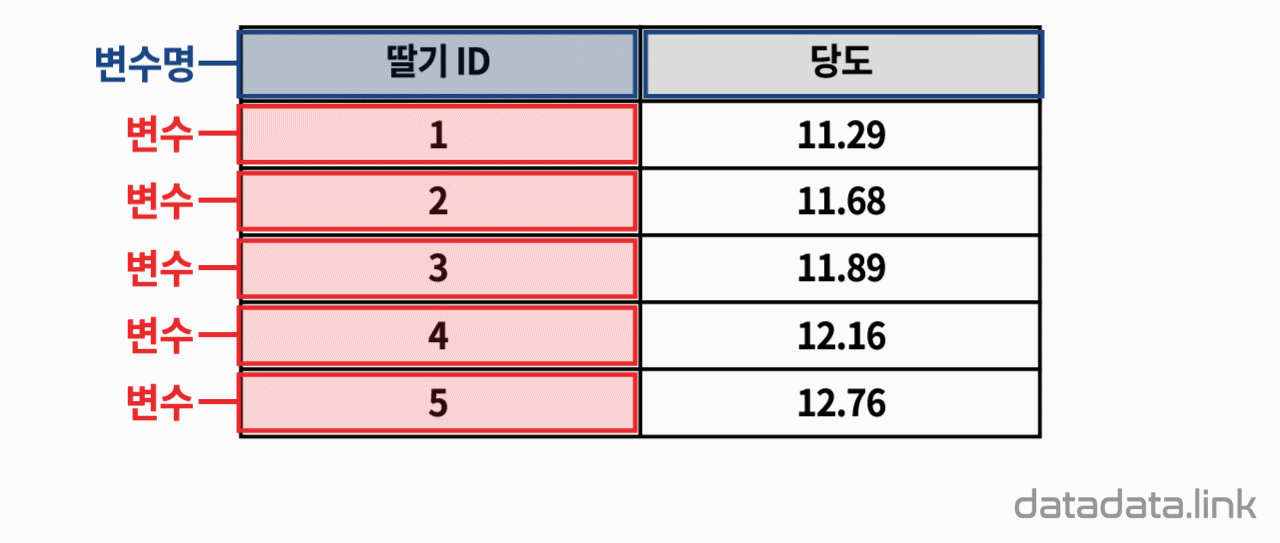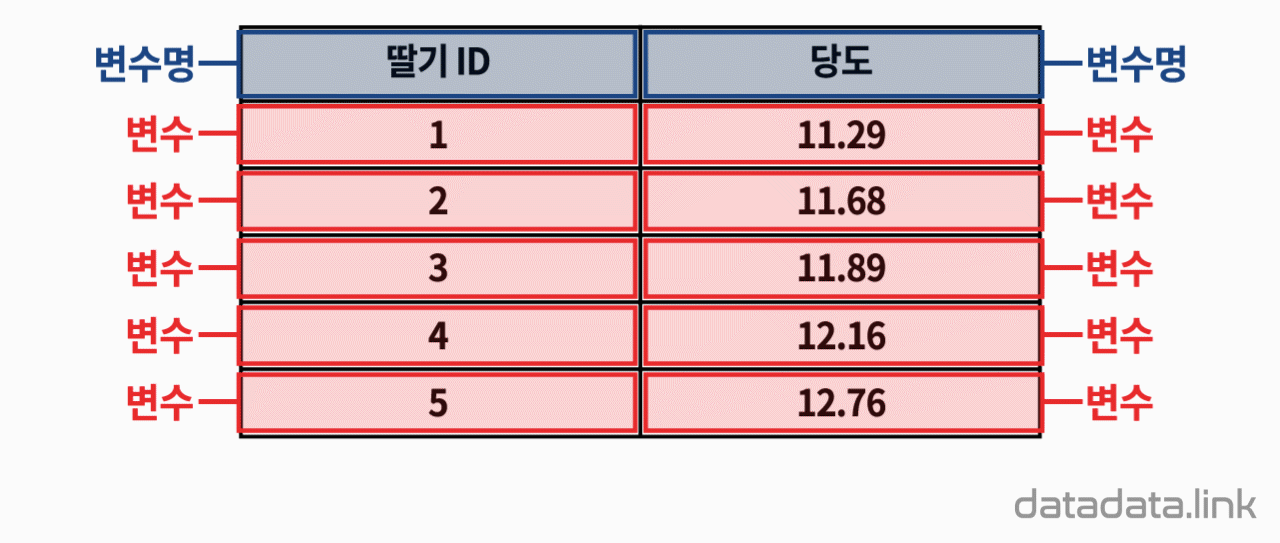
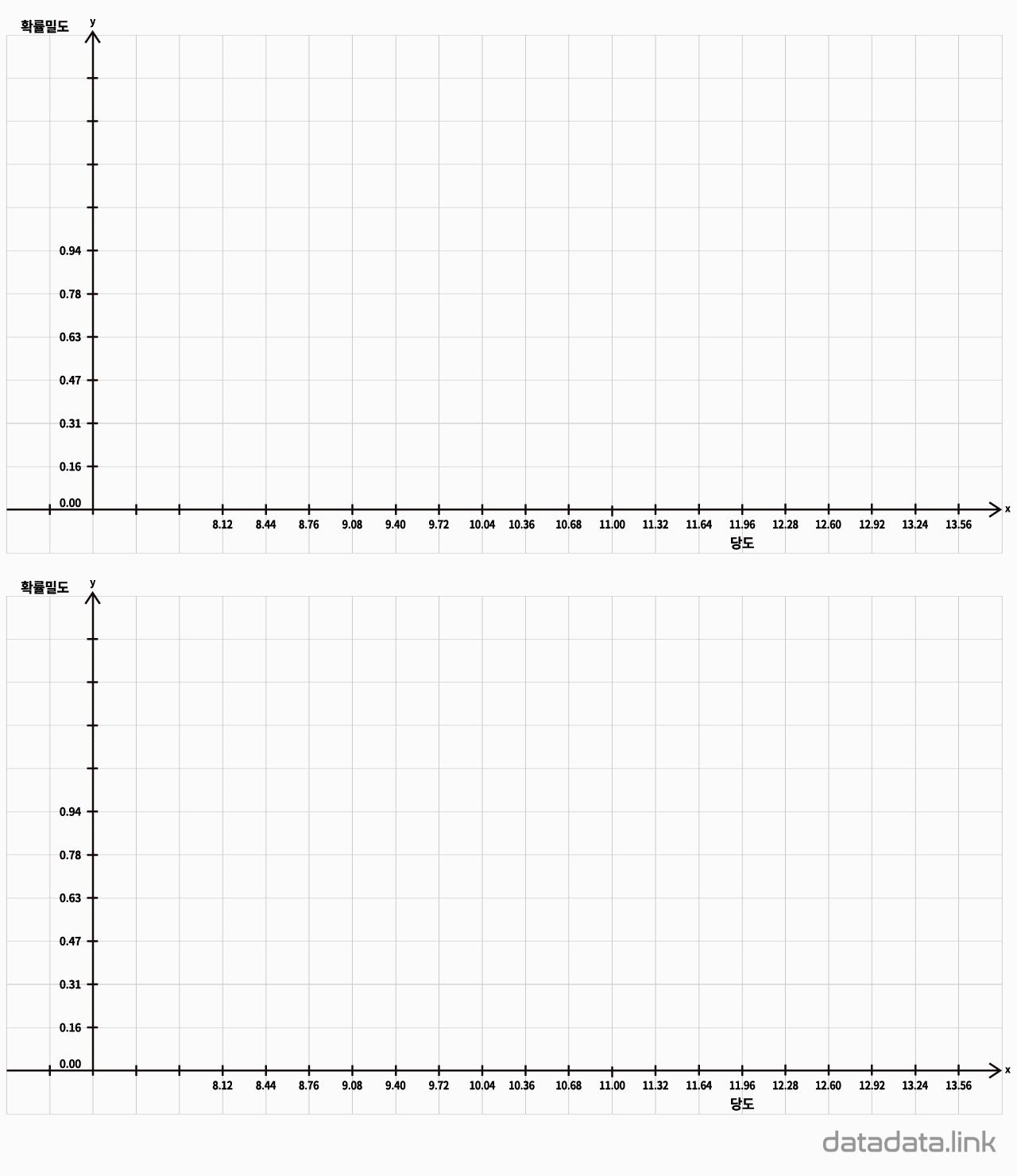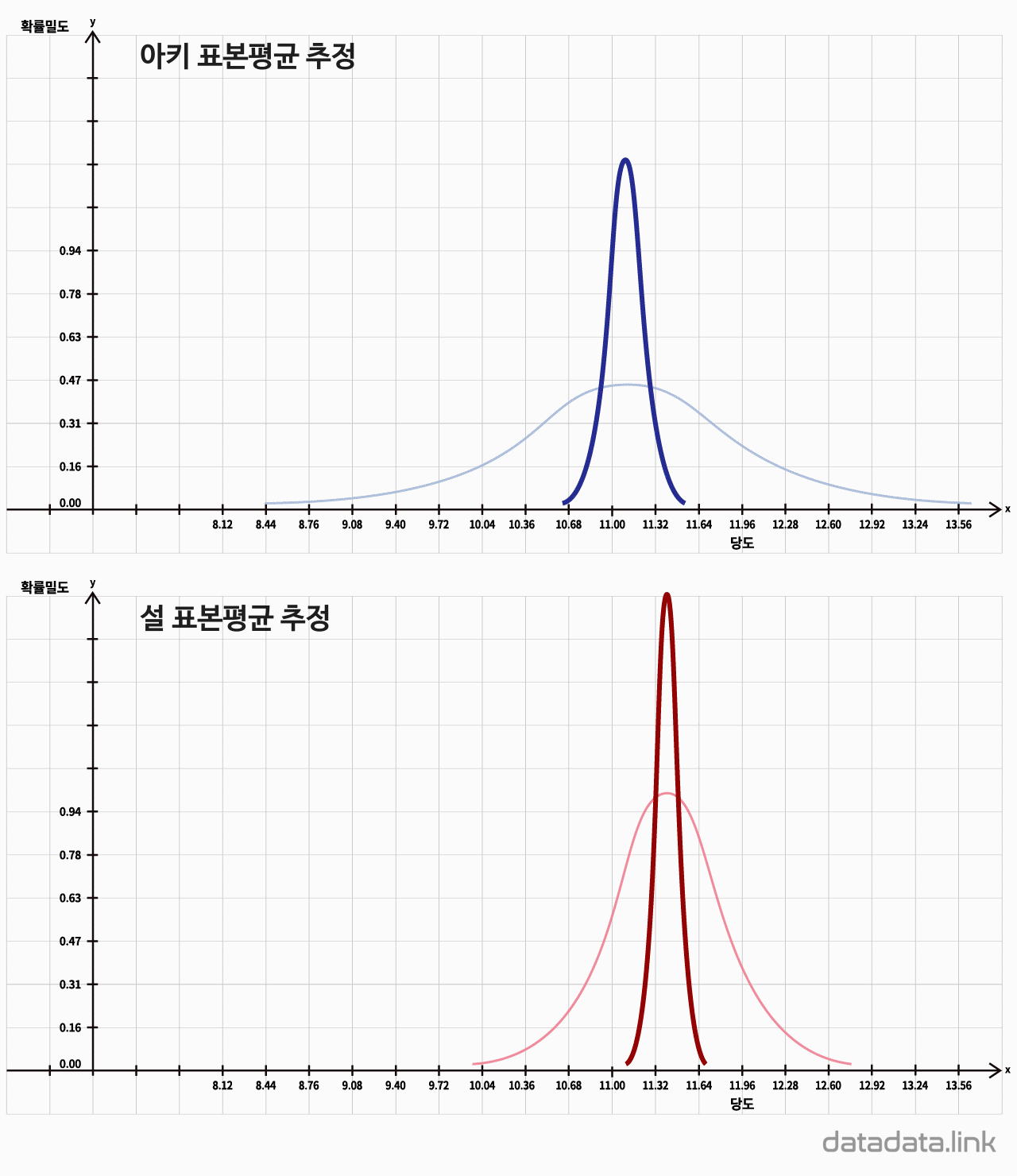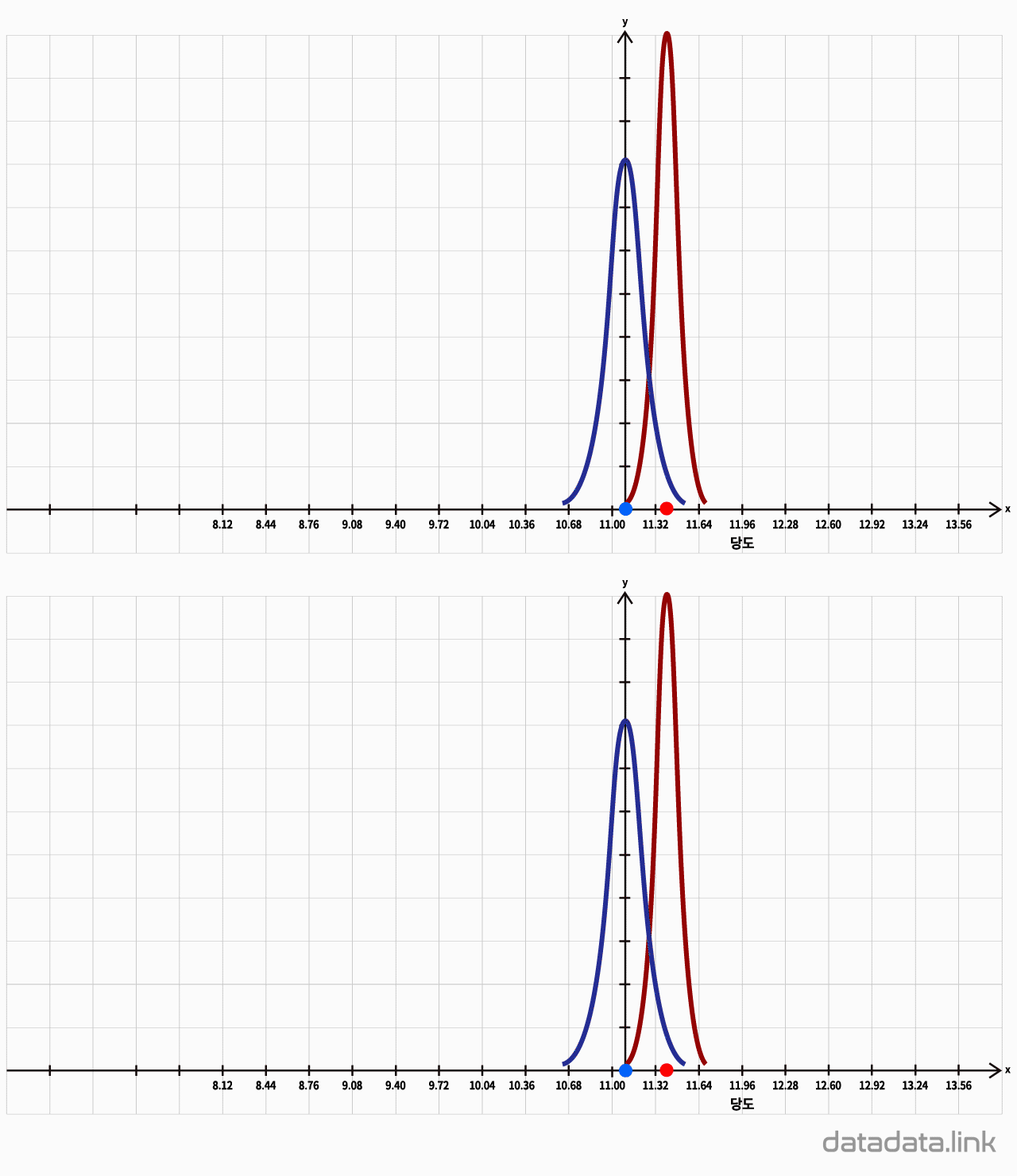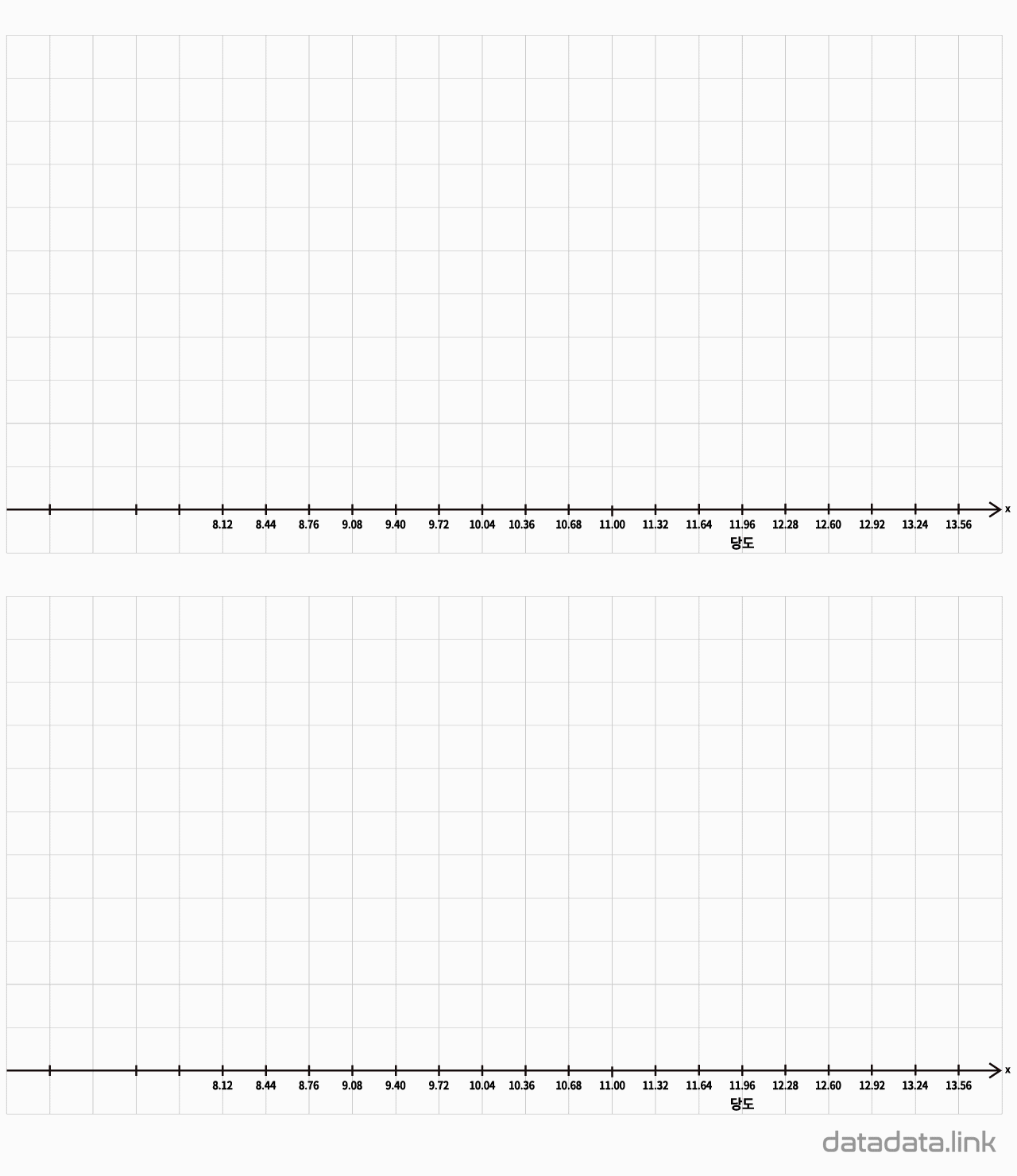
우선 승인기관에서 요구하는 적당한 조건의 임상시험 참가자를 모집합니다.  참가자를 다시 코로나 백신을 접종한 사람들을 실험군, 코로나 백신을 접종하지 않은 사람들을 대조군으로 구분합니다. 그리고 접종 후 일정기간이 지난 후 코로나에 감염되는 인원을 조사합니다.

그런데, 대조군은 아무래도 실험군에 비해 코로나에 걸리지 않기 위해 더욱 조심할 것이므로, 실험군과 대조군을 동일한 조건에서 실험을 했다고 보기 어렵습니다.

따라서, 이러한 임상시험에서는 대조군에도 접종을 하게 되는데, 이는 항체형성에 전혀 도움이 되지 않는 가짜 약제로 하는 접종으로, 위약 또는 플라시보(placebo)라고 합니다.

다음으로 임상시험에 참여하는 참가자의 입장에서 내가 실험군 혹은 대조군에 속해있다는 것을 안다면, 이 또한 임상시험 결과에 영향을 미치게 됩니다. 만약, 나에게 접종을 하는 사람 혹은 나를 관찰하는 사람의 표정이나 몸짓으로부터 내가 실험군 혹은 대조군에 속해있다는 정보를 얻을 수 있다면, 이 또한 문제가 됩니다. 따라서, 임상시험에서는 참가자 뿐만 아니라 실험자에게도 누가 실험군이고 대조군인지, 그리고 어떤 약이 백신이고, 위약인지 정보를 공개하지 않는데, 이를 이중맹검(더블블라인드, double-blind)라고 합니다. 

실험군과 대조군이 얼마나 공평하게 나누어져 있는가도 매우 중요한 문제입니다. 이 문제는 따로 다루겠습니다. 

A 검사로 양성반응이 나왔다면, 실제 병에 걸렸을 확률은 9%입니다.

A 검사는 다음과 같은 정확도를 가지고 있다고 알려져 있습니다.

병에 걸린 경우, 양성반응이 나타날 확률은 99%. 음성반응이 나타날 확률은 1%.

건강한데, 양성반응이 나타날 확률은 1%. 음성반응이 나타날 확률은 99%.

1,000명 중 1명 꼴로 걸리는 병이 있다고 할 때, 999명은 건강한 사람입니다. 건강한 사람 중 1%는 건강한데도 양성반응이 나옵니다. 999명의 1%는 9.99인데, 사람은 소수점으로 표현할 수 없으니까, 10명이라고 해보겠습니다.

감염된 사람 1명은 99% 확률로 양성반응이 나오므로, 이 1명도 양성반응이 나온다고 해보겠습니다.

따라서, 양성반응이 나오는 사람은 총 11명이고, 그 중 실제로 감염된 사람은 1명입니다. 계산해보면, 약 9%입니다.

B 검사로 양성반응이 나왔다면, 실제 병에 걸렸을 확률은 50%입니다.

B 검사는 다음과 같은 정확도를 가지고 있다고 알려져 있습니다.

감염된 경우, 양성반응이 나타날 확률은 99%. 음성반응이 나타날 확률은 1%.

건강한데, 양성반응이 나타날 확률은 0.1%. 음성반응이 나타날 확률은 99.9%.

1,000명 중 1명 꼴로 걸리는 병이 있다고 할 때,  999명은 건강한 사람입니다. 건강한 사람 중 0.1%는 건강한데도 양성반응이 나옵니다. 999명의 0.1%는 0.999인데, 사람은 소수점으로 표현할 수 없으니까, 1명이라고 해보겠습니다.

감염된 사람 1명은 99% 확률로 양성반응이 나오므로, 이 1명도 양성반응이 나온다고 해보겠습니다.

따라서, 양성반응이 나오는 사람은 총 2명이고, 그 중 실제로 감염된 사람은 1명입니다. 계산해보면, 50%입니다.

따라서 실제에서는, 병이 걸리지 않았는 데, 검사에서 양성반응으로 잘못 나타날 확률이 0.1%보다는 훨씬 작은 검사방법이 있어야겠습니다.

모집단의 점수가 정규분포를 이룬다면, 수학점수가 더 높습니다.

수학점수와 영어점수의 평균과 표준편차가 다르기 때문에 이를 표준화해서 비교합니다. 내 점수에서 평균을 빼고, 표준편차로 나누면 표준화된 수치를 얻을 수 있습니다.

표준화 후의 수학점수는 2.50이고, 영어점수는 1.67입니다. 수학점수가 영어점수보다 더 높습니다. 

수학점수는 상위 1%이내, 영어점수는 상위 5% 이내에 해당합니다.

수학점수가 50점 이상인 사람은 전체 시험을 본 사람 중 0.7% 이내입니다. 영어점수가 90점 이상인 사람은 전체 시험을 본 사람 중 4.8%이내입니다.

딸기의 과중을 가로축으로, 당도를 세로축으로 하는 딸기의 2차원 산점도를 그려보면, 딸기의 과중과 당도는 선형의 관계가 나타납니다.

하나의 딸기가 가지는 과중과 당도의 관계를 알기 위해, 과중을 가로축으로, 당도를 세로축으로 하는 딸기의 2차원 산점도를 그립니다. 위의 데이터에서 요소는 딸기이고, 변수는 과중과 당도입니다. 상관관계는 동일한 요소의 변수간 관계를 파악하는 것입니다. 

어느 정도 상관이 있는지, 표준화한 수치로 나타낸 것인 상관계수입니다.

상관계수는 -1부터 1까지의 값을 가집니다. 두 변수, 과중과 당도가 같은 방향으로 동일한 크기로 변화하면 상관계수는 1이 되고, 반대 방향으로 동일한 크기로 변화하면 상관계수는 -1이 됩니다.

우리나라의 딸기품종 설향은 겨울철에 맛있습니다.

딸기는 전년도 늦가을부터 다음해 초여름까지 재배하면서 4~5번 정도 열매를 수확합니다. 우리나라에서 유통되는 딸기의 70% 이상을 차지하는 설향은 추위에 강합니다. 겨울에 수확하는 설향은 익는데, 시간이 좀 더 걸리고 광합성을 오래함으로써, 봄철에 수확하는 설향에 비해 당도가 높습니다.
위에 사용한 데이터는 설향을 특성을 반영하여 학습용으로 가공한 데이터입니다.

국회의원 재산 평균 94억원?

2013년 3월 29일 국회 공직자윤리위원회가 공개한 296명의 국회의원 재산 평균(산술평균)은 94억 9000만원입니다.

그런데, 정몽준 의원, 고희선 의원을 제외하고, 평균을 계산하면 23억 3000만원이었습니다. 두 의원의 재산은 각각 1조 9249만원, 1984억원이었습니다.

데이터(값들의 집합)는 대표하는 값이 있습니다.

데이터를 대표하는 값에는 평균(mean), 중앙값(median), 최빈값(mode)이 있습니다.

중앙값(median)은 데이터를 크기 순서로 나열할 때 중앙에 놓이는 값입니다.

중앙값은  특별히 크거나 작은 변수값이 있는 경우에 왜곡이 심하지 않아 데이터의 대표값으로 많이 쓰입니다.

최빈값(mode)은 변수값 중 가장 빈도수가 큰 변수값입니다.

평균에는 산술평균, 가중평균 등이 있습니다.

평균은 중앙값과 비교하여 어느 한 변수값이 아주 크거나 작은 경우 왜곡이 나타납니다.

보통 평균이라고 하면 산술평균을 의미합니다.

가중평균(weighted mean)은 산술평균의 다른 변형형태로 각 변수값에 가중치를 곱하여 평균을 구합니다.

특별히 변수가 확률변수이고 가중치의 합이 1이 되면 가중평균은 기대값이 됩니다.

여기서 각 확률변수의 가중치는 그 확률변수의 확률이 됩니다.

애니메이션에서 가로축은 확률변수를, 세로축은 확률밀도함수값을 표시합니다.

애니메이션처럼 확률밀도함수가 정규분포를 이루면 평균, 중앙값, 최빈값은 같은 확률변수값을 가집니다.

그러나 편향이 일어날 경우 다른값을 가집니다.

평균은 무게중심을 나타내는 확률변수값입니다.

중앙값은 지나는 직선의 양쪽 면의 면적이 같은 확률변수값입니다.

최빈값은 확률밀도함수의 정점을 나타내는 확률변수값입니다.

데이터 값 중에서 극단적으로 크거나 작은 값이 있는 경우, 산술평균보다 중앙값을 대표값으로 사용하는 것이 나을 수 있습니다.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

위의 값을 모두 더하면 55이고, 이를 갯수 10으로 나누면 평균은 5.5 입니다. 중앙값은 5와 6의 중간인 5.5입니다. 데이터가 좌우 대칭으로 분포되어 있으면, 평균과 중앙값은 같습니다.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 100

위의 값을 모두 더한 값은 155이고, 이를 갯수 11로 나누면, 평균은 14.09이고, 중앙값은 6입니다.

가설을 세웁니다.

우리가 새로운 딸기 품종을 만들었는데, 이 품종이 기존의 딸기 품종과는 다르다는 것을 검정하는 사례로 살펴보겠습니다.

“새로운 딸기 품종은 기존의 딸기 품종과 같다”라는 영가설(귀무가설)을 세웁니다.

가설을 검정하기 위해서 검정할 확률변수를 정하고 표본의 통계량을 구합니다.

소비자가 딸기를 선택하는 가장 중요한 기준은 당도이므로 당도를 확률변수로 정합니다.

기존 품종의 당도의 모수(parameter)는 평균 11 브릭스(Brix), 표준편차 1로 알려져 있습니다.

새로 개발한 딸기 품종 10알의 당도를 측정하여서 표본통계량을 구하였습니다. 당도 평균은 12 브릭스(Brix), 표준편차는 2 입니다.

“두 딸기품종의 당도의 평균 차이가 없다(0이다)”라는 영가설을 검정합니다.

“새로 개발한 딸기 품종의 당도 평균은 기존 품종과 차이가 없다.”

위와 같이 우리가 증명하고 싶은 것과 반대의 가설을 영가설(혹은 귀무가설. Null Hypothesis)이라고 하고, 이 영가설을 기각할 수 있게 되면, 반대인 대립가설(혹은 연구가설. Alternative Hypothesis or Research Hypothesis)을 채택할 수 있습니다.

5% 유의수준으로 이 가설을 검정한다면, 우리가 측정한 10알의 샘플(표본) 데이터로부터 95% 신뢰구간을 구해볼 수 있습니다.

11.62~13.38 Brix

95% 신뢰구간 내에 기존 품종의 당도 평균인 11이 있습니다. 이러한 경우에는 영가설을 채택할 수 있습니다. 즉, 새로 만든 딸기 품종이 기존 품종과 다르다고 할 수 없습니다.

또 다른 표본을 추출해서 가설검정을 해 봅니다.

새로 개발한 딸기 품종 10알을 다시 추출해서 측정하였습니다. 평균은 13, 표준편차는 2로 측정이 되었습니다. 95% 신뢰구간을 구해보면 다음과 같습니다.

11.76~14.24 Brix

기존 품종의 당도 평균 11은 위에서 구한 95% 신뢰구간 밖에 있습니다. 이러한 경우, 영가설을 기각하고, 새로 만든 딸기 품종이 기존 품종과 다르다고 할 수 있습니다.

두 번의 샘플을 측정해서 가설검정을 하였는데, 그 결과가 상반되게 나왔습니다.

두 표본을 합쳐서 표본통계량을 구해보겠습니다.

표본크기는 20, 평균은 12.5, 표준편차는 2입니다. 95% 신뢰구간을 구해보면 다음과 같습니다. 

11.62~13.38 Brix

기존 품종의 당도 평균11은 위에서 구한 95% 신뢰구간 밖에 있습니다. 영가설을 기각하고, 새로 만든 딸기 품종이 기존 품종과 다르다고 할 수 있습니다.

샘플의 크기가 커질수록 신뢰구간이 좁아진다는 것을 알 수 있습니다. 가설검정이 더 정교해졌습니다.

샘플의 크기가 30개 미만인 경우, t분포를 사용하는 것이 일반적이지만, 보다 쉬운 이해를 위해 위의 예에서는 둘 다 z분포를 사용했습니다.

 가설검정의 결과는 가설의 채택 또는 기각입니다.

가설을 세웁니다.

우리가 새로운 딸기 품종을 만들었는데, 이 품종이 기존의 딸기 품종과는 다르다는 것을 검정하는 사례로 살펴보겠습니다.

“새로운 딸기 품종은 기존의 딸기 품종과 같다”라는 영가설(귀무가설)을 세웁니다.

가설을 검정하기 위해서 검정할 확률변수를 정하고 표본의 통계량을 구합니다.

소비자가 딸기를 선택하는 가장 중요한 기준은 당도이므로 당도를 확률변수로 정합니다.

기존 품종의 당도의 모수(parameter)는 평균 11 브릭스(Brix), 표준편차 1로 알려져 있습니다.

새로 개발한 딸기 품종 10알의 당도를 측정하여서 표본통계량을 구하였습니다. 당도 평균은 12 브릭스(Brix), 표준편차는 2 입니다.

“두 딸기품종의 당도의 평균 차이가 없다(0이다)”라는 영가설을 검정합니다.

“새로 개발한 딸기 품종의 당도 평균은 기존 품종과 차이가 없다.”

위와 같이 우리가 증명하고 싶은 것과 반대의 가설을 영가설(혹은 귀무가설. Null Hypothesis)이라고 하고, 이 영가설을 기각할 수 있게 되면, 반대인 대립가설(혹은 연구가설. Alternative Hypothesis or Research Hypothesis)을 채택할 수 있습니다.

5% 유의수준으로 이 가설을 검정한다면, 우리가 측정한 10알의 샘플(표본) 데이터로부터 95% 신뢰구간을 구해볼 수 있습니다.

10.76~13.24 Brix

95% 신뢰구간 내에 기존 품종의 당도 평균인 11이 있습니다. 이러한 경우에는 영가설을 채택할 수 있습니다. 즉, 새로 만든 딸기 품종이 기존 품종과 다르다고 할 수 없습니다.

표본의 크기를 키우면, 동일한 신뢰수준에서 신뢰구간이 줄어듭니다.

이번에는 새로 개발한 딸기 품종 100알을 측정하였습니다. 평균은 11.8, 표준편차는 2로 측정이 되었습니다. 95% 신뢰구간을 구해보면 다음과 같습니다.

11.40~12.20 Brix

기존 품종의 당도 평균 11은 위에서 구한 95% 신뢰구간 밖에 있습니다. 이러한 경우, 영가설을 기각하고, 새로 만든 딸기 품종이 기존 품종과 다르다고 할 수 있습니다. 물론, 정말 그러한지는 별개의 문제입니다. 영가설이 사실인데, 이를 잘못 기각하는 오류를 1종오류라고하고, 사실이 아닌 영가설을 잘못 채택하는 오류를 2종 오류라고 합니다.

샘플의 크기가 30개 미만인 경우, t분포를 사용하는 것이 일반적이지만, 보다 쉬운 이해를 위해 위의 예에서는 둘 다 z분포를 사용했습니다.

설향이라는 우리나라의 대표적인 딸기 품종이 있습니다.

이 품종의 당도 평균을 알고 싶은데, 모든 설향을 다 측정할 수는 없어서, 스무알만 추출해서 당도를 측정해보았습니다.

설향 스무알의 당도 평균은 11.56, 분산 0.21, 표준편차 0.46이 나왔습니다.

그런데, 이 샘플로부터 얻은 평균을 전체 평균과 동일하다고 단언하기가 힘들어서, 95% 신뢰구간으로 표현해 보았습니다.

11.35 ~ 11.76

그럼, 전체 설향 중 95%의 당도는 이 범위 내에 있을까요?

이 신뢰구간은 다음의 가정을 내포하고 있습니다.

우리가 설향 스무알을 추출한 방식이 랜덤해야 합니다. 

우리가 추출한 스무알의 샘플은 무한하게 추출할 수 있는 샘플들 중 하나입니다. 

샘플의 평균은 수많은 샘플의 평균들 중 하나입니다.

샘플의 평균은 샘플을 추출할 때마다 달라지게 되고, 그 샘플로부터 구한 신뢰구간도 달라지게 됩니다.

전체 설향의 당도 평균은 이 신뢰구간 내에 있을 수도 있고, 아닐 수도 있습니다.

95% 신뢰수준이란, 샘플을 랜덤하게 추출해서, 95% 신뢰구간을 구하면, 스무번 중 한 번은 전체 평균이 벗어날 수 있다는 의미입니다. 스무번 중 한 번이란 확률적으로는 5%이고, 이를 유의수준이라고 표현합니다. 

Block "2934" not found

왜 표본분산은 표본의 크기인 n인 아닌, n-1로 나눌까요?

표본을 랜덤하게, 그리고 무한하게 추출한다고 할 때, 표본분산의 기대값을 모분산과 같게 하기 위해서입니다.

다음 네 숫자의 사례로 살펴보겠습니다.

1, 2, 3, 4

네 숫자를 모두 더해서, 개수로 나누면 평균이 됩니다. 

평균은 2.5입니다.

만약, 미지의 수, x와 위의 네 숫자와의 차이의 제곱의 합을 최소로 하는 x를 구해보면 어떻게 될까요? 수식으로 표현하면 다음과 같습니다.

$y=(1-x)^2+(2-x)^2+(3-x)^2+(4-x)^2$

위의 식을 그래프로 표현하면 다음과 같습니다. 

y의 값을 최소로 하는 x의 값은 2.5이고, 평균과 같습니다.

즉, 편차제곱의 합을 구하는데, 평균을 기준으로 할 때, 그 값이 최소가 됩니다.

만약, 위의 1, 2, 3, 4가 우리가 알고 싶은 미지의 모집단으로부터 추출한 표본이라면 어떻게 될까요?

미지의 수 x 자리에 모집단의 평균인 $\mu$를 넣어보겠습니다.

$y=(1-\mu)^2+(2-\mu)^2+(3-\mu)^2+(4-\mu)^2$

모집단의 평균이 1, 2, 3, 4라는 표본의 평균과 같을수도 있고 다를 수도 있습니다. 모집단의 평균이 표본 평균과 다르다면, 모평균을 기준으로 한 편차제곱의 합은 표본평균을 기준으로 한 편차제곱의 합보다 커지게 됩니다. 이 커진만큼을 조정하기 위해 n이 아닌 n-1로 나누게 됩니다. 

표본 내 편차제곱의 합과 모집단의 편차제곱의 합의 크기 사이의 관계를 수식으로 살펴보겠습니다.

$X_k$ : 확률변수

$\bar{X}$ : 표본평균

$\mu$ : 모평균

$\sigma^2$ : 모분산

$S^2$ : 표본분산

$\sum_{k=1}^n\left(X_k-\bar{X}\right)^2=\sum_{k=1}^{n}\left((X_k-\mu)+(\mu-\bar{X})\right)^2$

$=\sum_{k=1}^{n}\left((X_k-\mu)^2 + 2(X_k-\mu)(\mu-\bar{X})+(\mu-\bar{X})^2\right)$

$=\sum_{k=1}^{n}(X_k-\mu)^2 + \sum_{k=1}^{n}2(X_k-\mu)(\mu-\bar{X})+\sum_{k=1}^{n}(\mu-\bar{X})^2$

$=\sum_{k=1}^{n}(X_k-\mu)^2 + 2n(\bar{X}-\mu)(\mu-\bar{X})+n(\mu-\bar{X})^2$

$=\sum_{k=1}^{n}(X_k-\mu)^2-n(\bar{X}-\mu)^2$

$=\left(n\sigma^2-n\frac{\sigma^2}{n}\right)$

$=(n-1)\sigma^2$

위 식의 핵심은 표본 내 편차제곱의 합에서 모분산을 도출해낼 수 있도록 모평균을 빼고 더해주는 것입니다.

$\sum_{k=1}^n\left(X_k-\bar{X}\right)^2=(n-1)\sigma^2$

$E(\frac{\sum_{k=1}^n\left(X_k-\bar{X}\right)^2}{(n-1)})=\sigma^2$

$E(S^2)=\sigma^2$

표본 내 편차제곱의 합의 기대값은 모분산에 n-1을 곱한 것과 같습니다. 

표본분산을 모분산의 불편추정량(편의가 없는 추정량. Unbiased Estimator)로 사용하기 위해서는 표본 내 편차제곱의 합을 n이 아닌 n-1로 나누어줍니다. 

만약, 표본 내 편차제곱의 합을 n으로 나눈다면, 이 값의 기대값은 모분산과 다르기 때문에, 모분산에 대한 편의가 있는 추정량(Biased Estimator)이 됩니다.