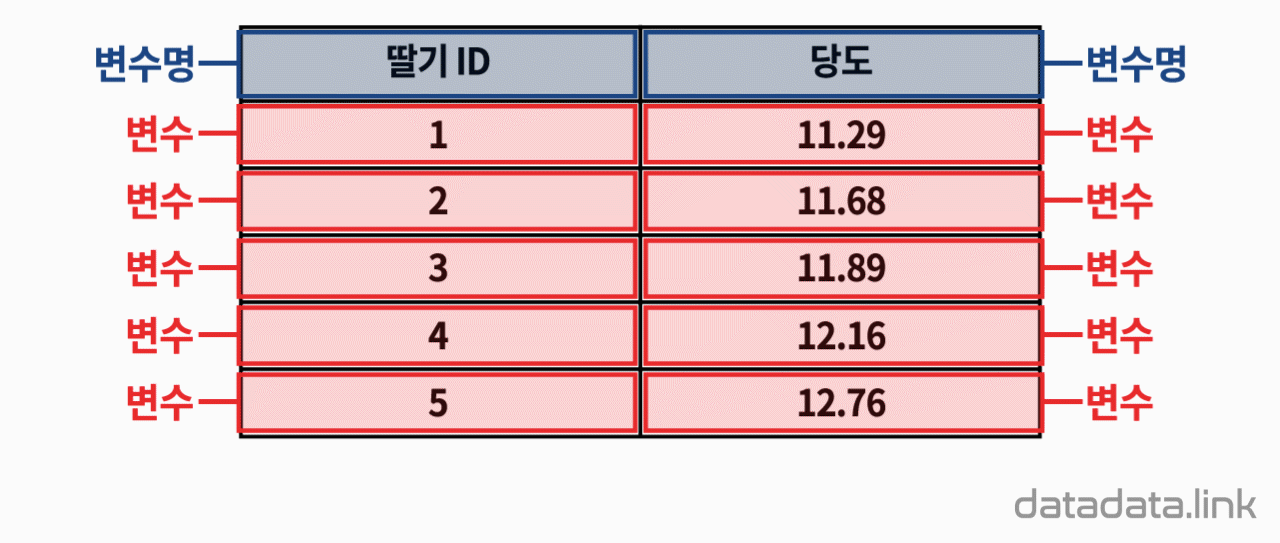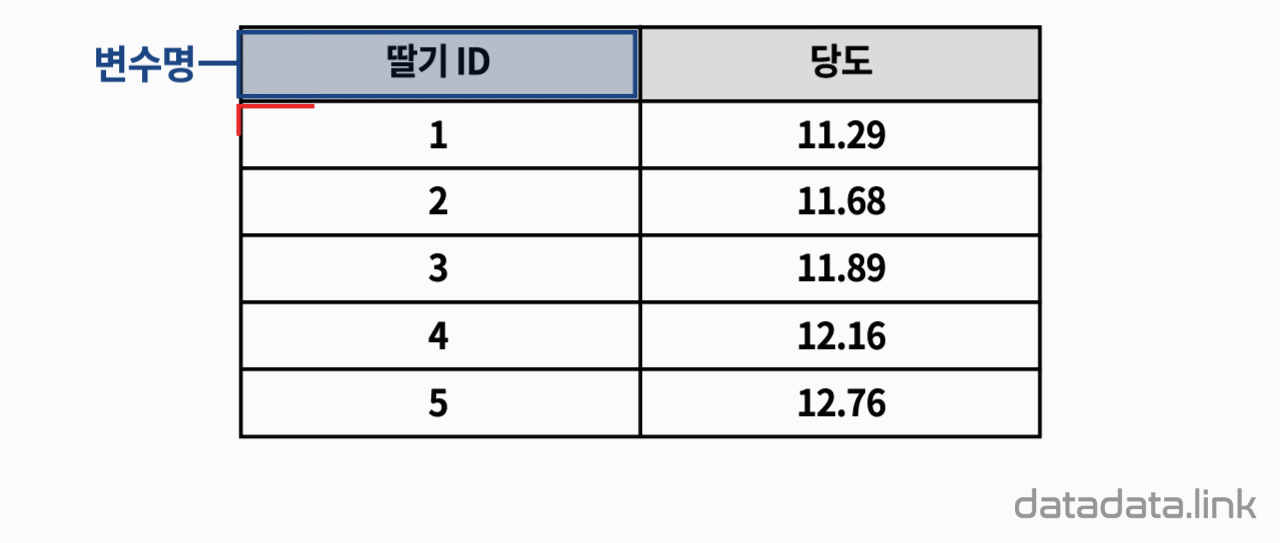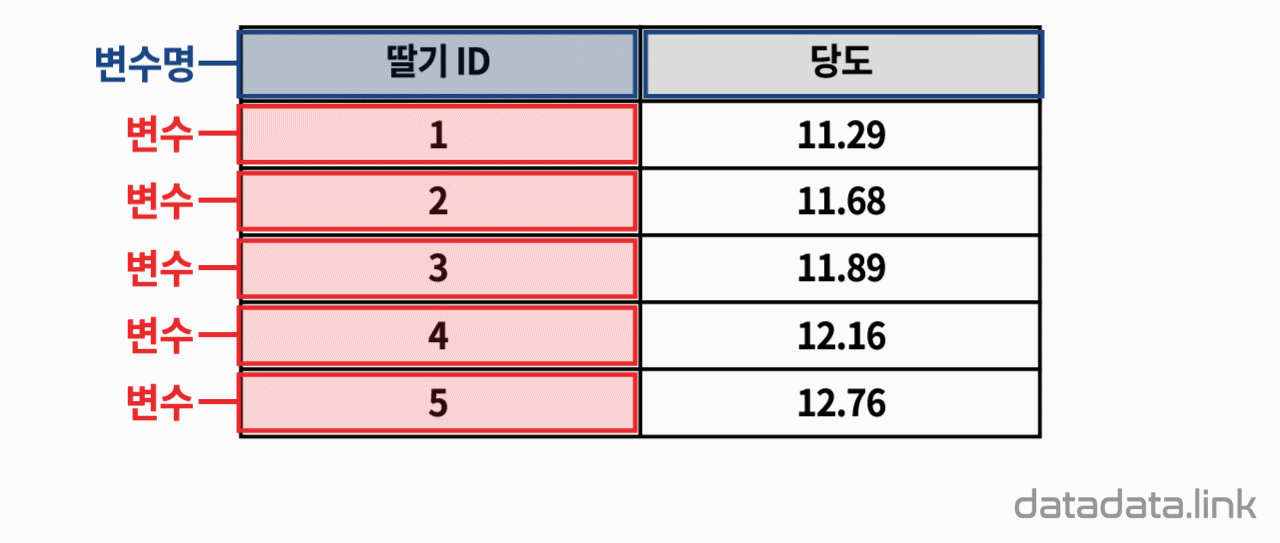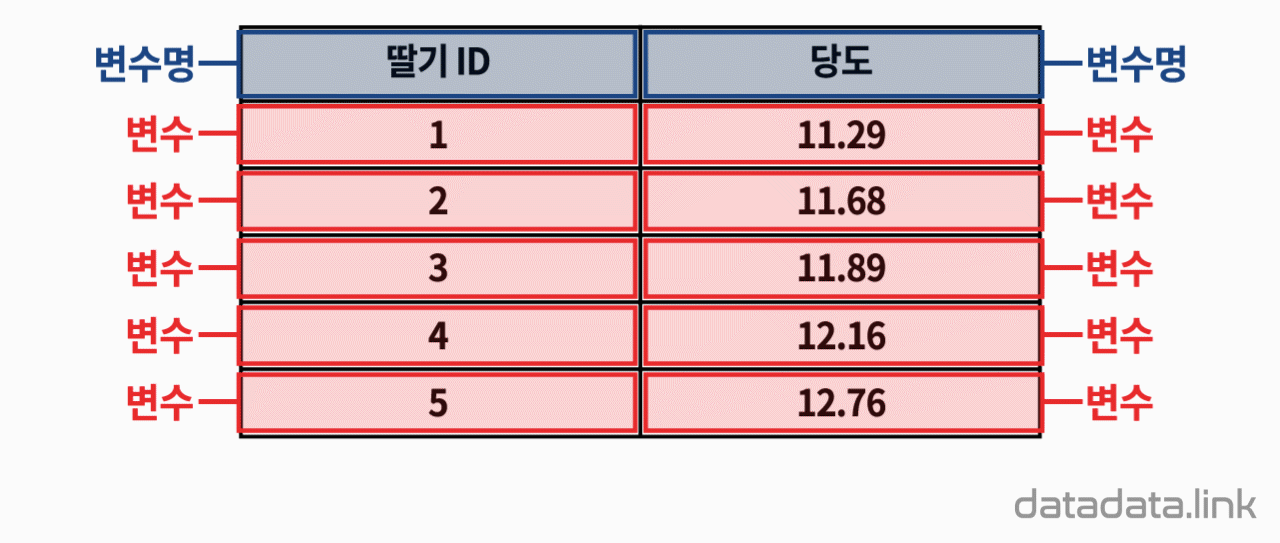
왜 편차제곱을 사용할까
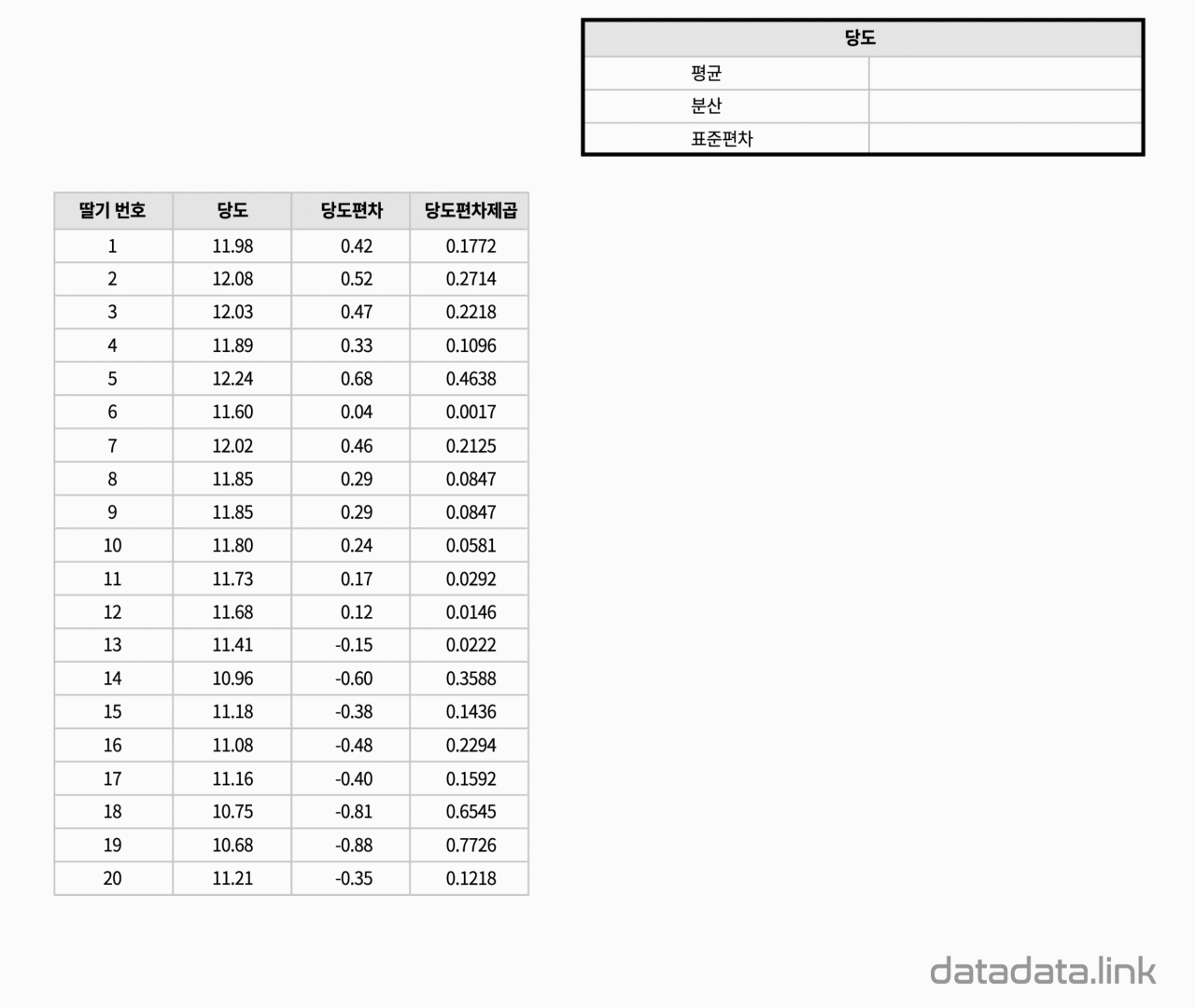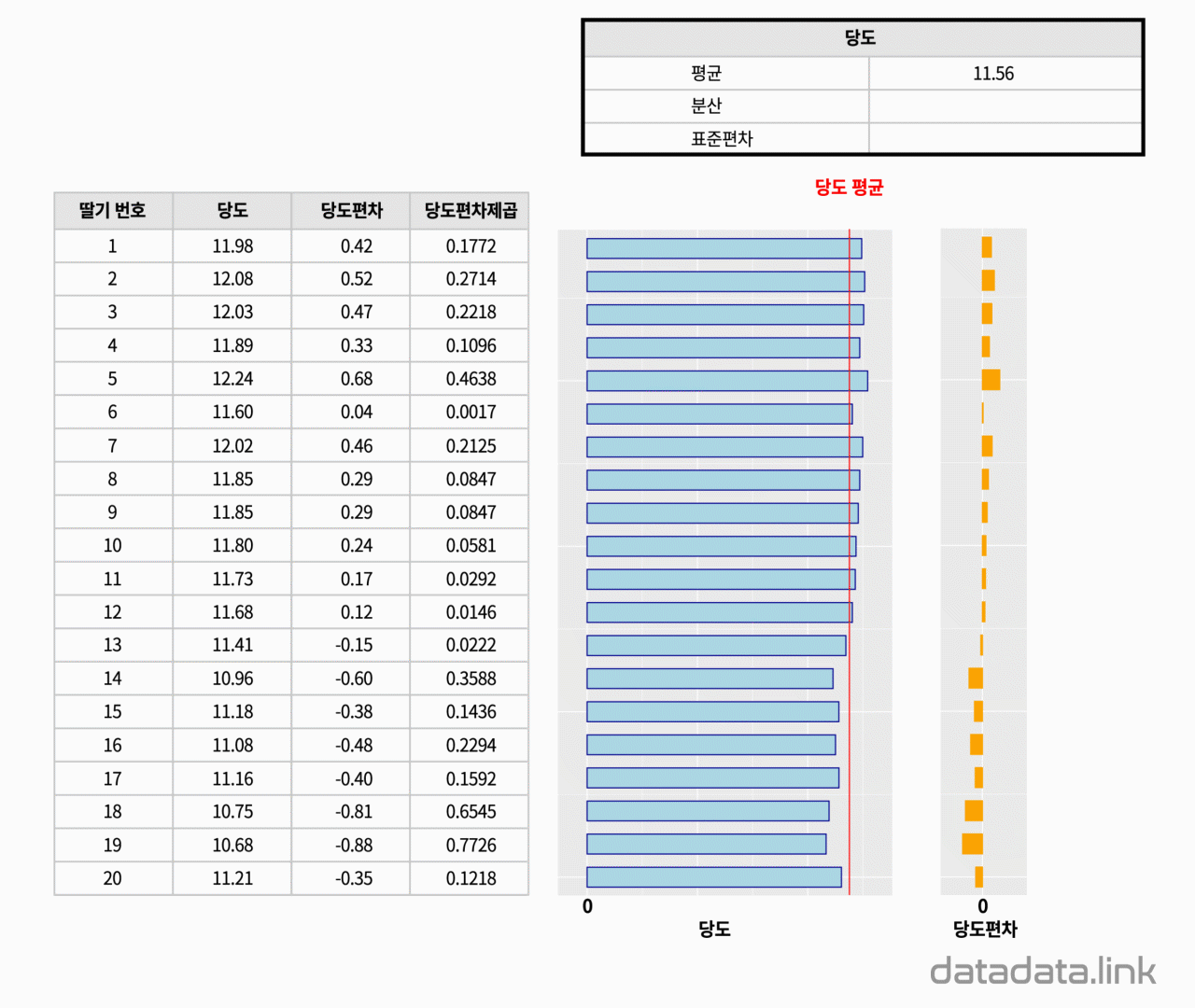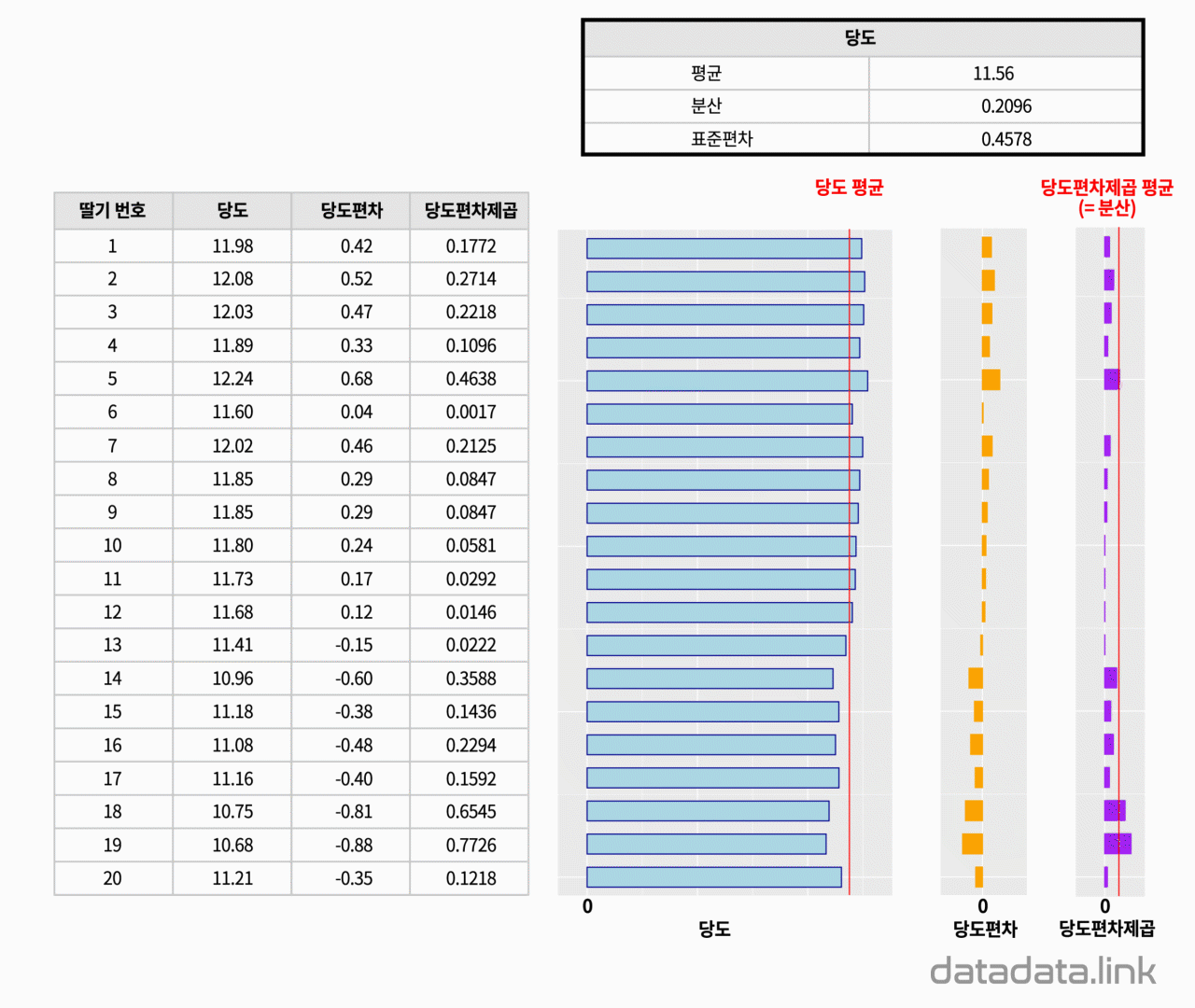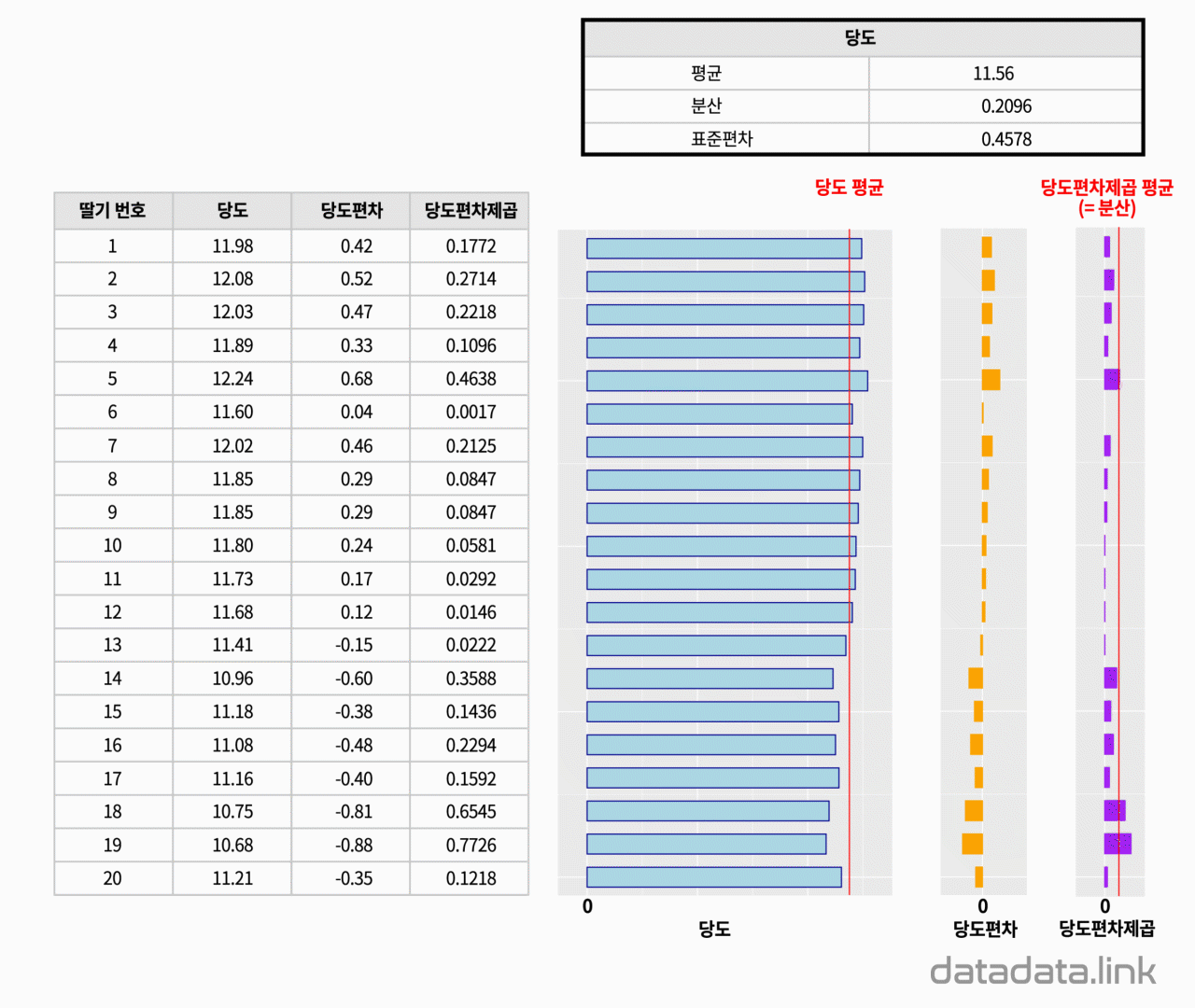
왜 복잡하게, 편차가 아닌 편차제곱을 사용할까요?
편차를 각 ‘확률변수-평균’으로 정의한다면, 편차의 합은 항상 0이 되고, 평균도 0이 되어서 데이터가 평균으로부터 얼마만큼 퍼져있는지 정도를 알기 어렵습니다.
그럼, 편차 절대값을 사용하면 되지 않을까요?
다음 네 숫자의 사례로 살펴보겠습니다.
1, 2, 3, 4
네 숫자를 모두 더해서, 개수로 나누면 평균이 됩니다.
평균은 2.5입니다.
만약, 미지의 수, x와 위의 네 숫자와의 차이의 절대값의 합을 최소로 하는 x를 구해보면 어떻게 될까요? 수식으로 표현하면 다음과 같습니다.
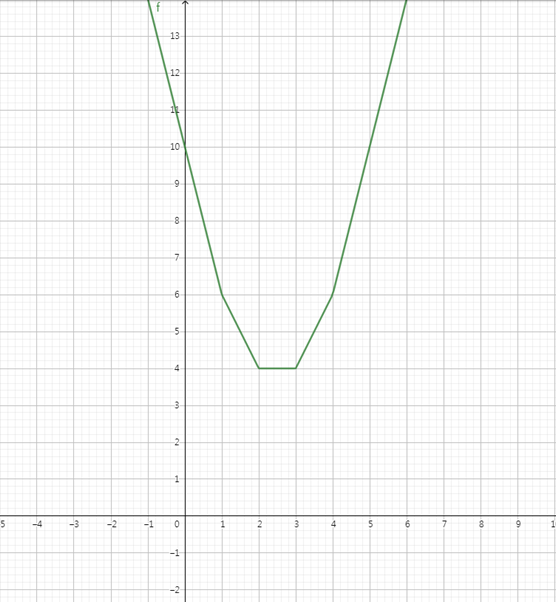
y=|1-x|+|2-x|+|3-x|+|4-x|
위의 식을 그래프로 표현하면 다음과 같습니다.
y를 최소로 하는 x의 값은 2와 3 사이의 모든 숫자가 됩니다.
만약, 미지의 수, x와 위의 네 숫자와의 차이의 제곱의 합을 최소로 하는 x를 구해보면 어떻게 될까요? 수식으로 표현하면 다음과 같습니다.
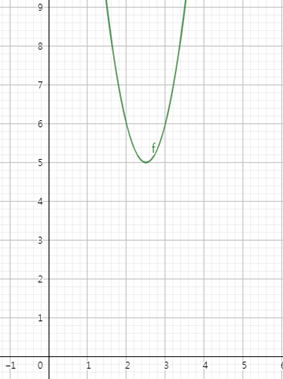
$y=(1-x)^2+(2-x)^2+(3-x)^2+(4-x)^2$
위의 식을 그래프로 표현하면 다음과 같습니다.
y의 값을 최소로 하는 x의 값은 2.5 하나이고, 평균과 같습니다.
만약, 현재 뿐만 아니라 미래에도 계속 생성되는 데이터로부터 평균을 찾아나간다면, 편차절대값보다 편차제곱을 사용하는 것이 효과적입니다.
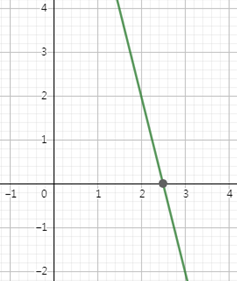
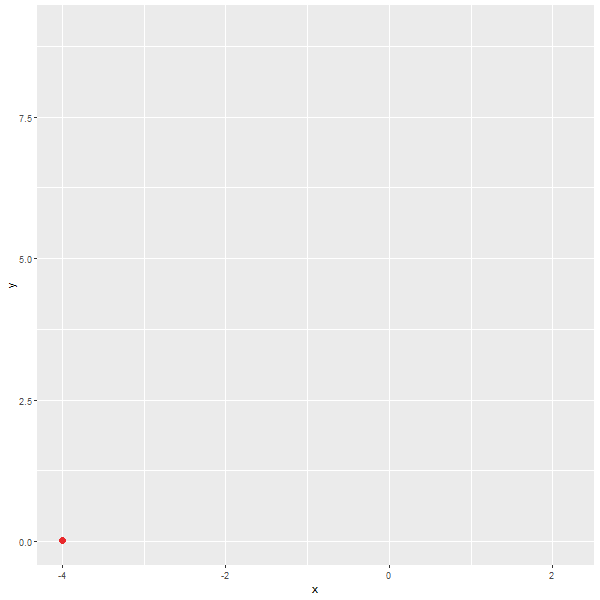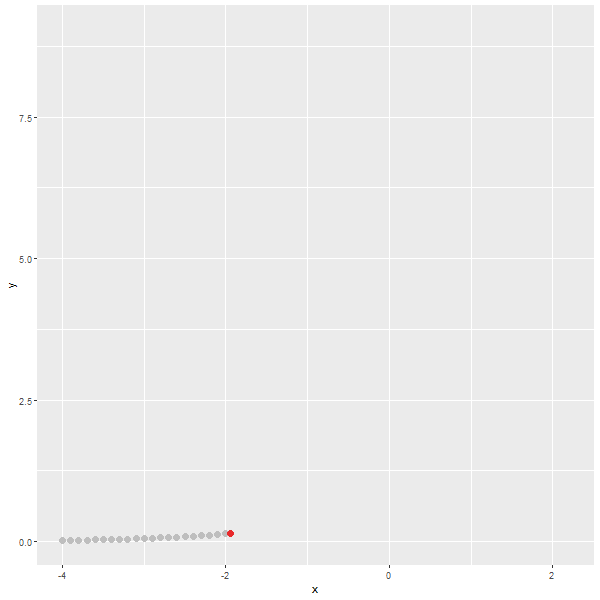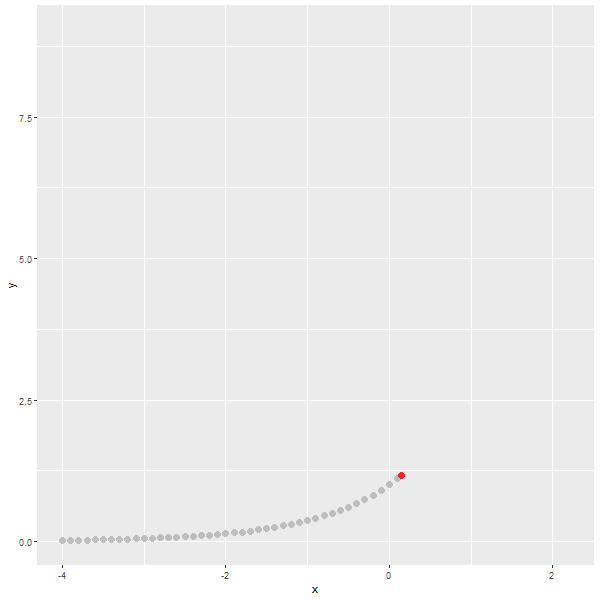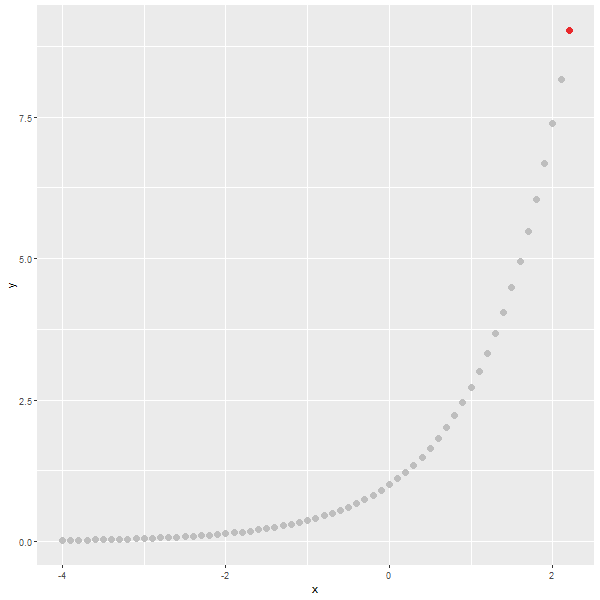
마지막으로 다음의 식을 그래프로 표현해보겠습니다.
y=(1-x)+(2-x)+(3-x)+(4-x)
x의 값이 작아질수록, y의 값이 작아집니다. x의 값이 2.5일때, y의 값은 0이 됩니다.