2차원 산점도 ?
2D scatter plot ?
2.1. 2차원 산점도
1. 애니메이션
2. 설명
2.1. 2차원 산점도
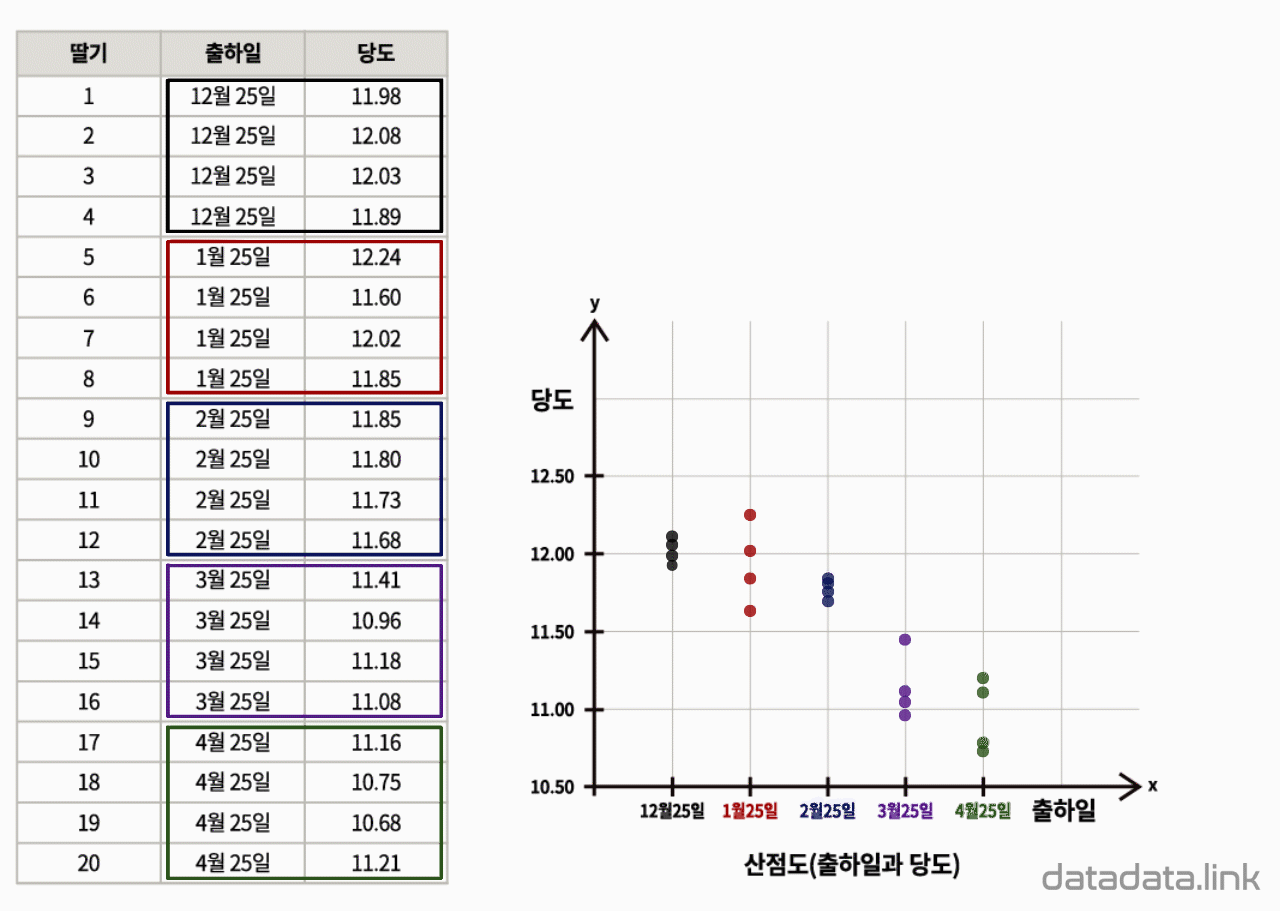
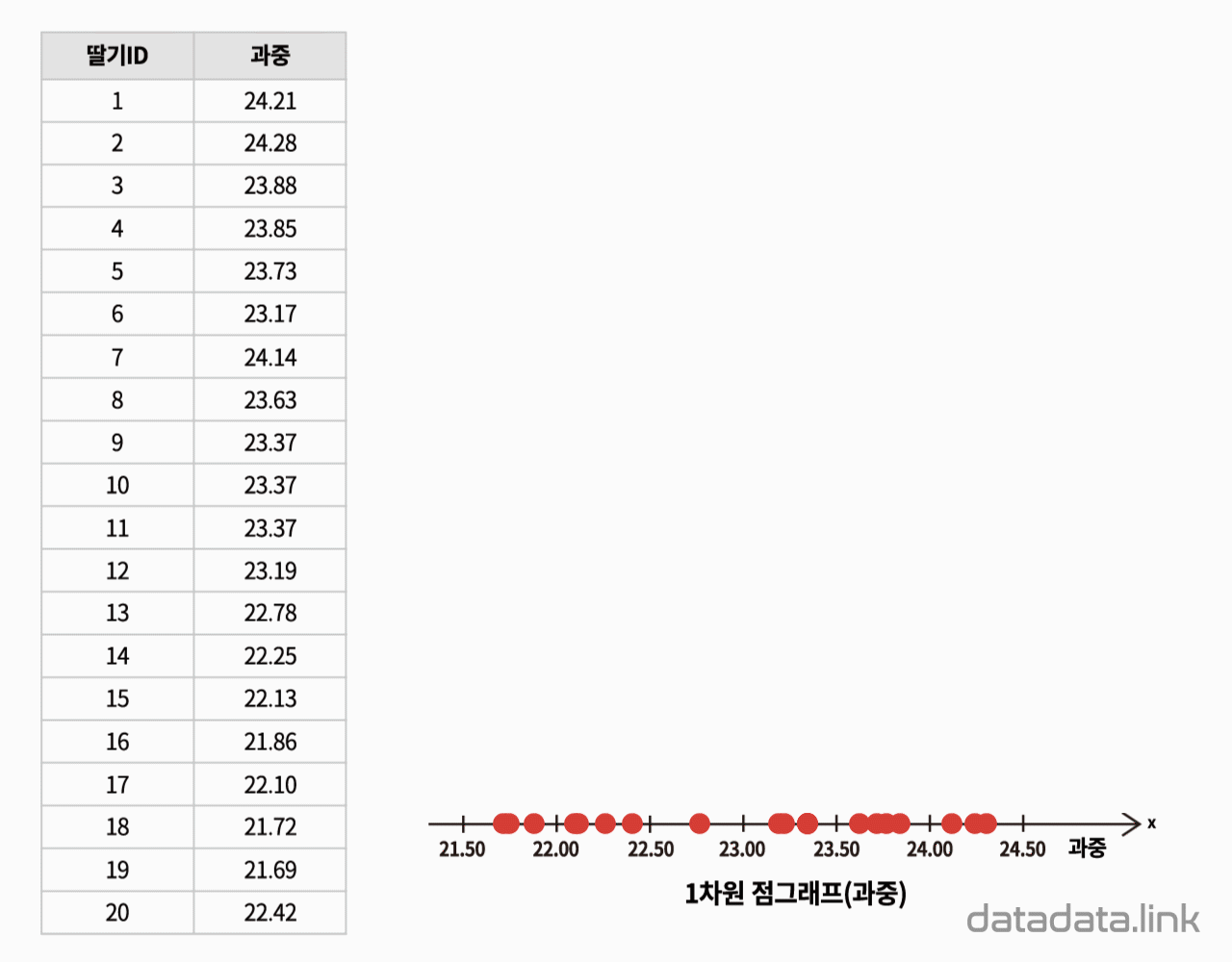
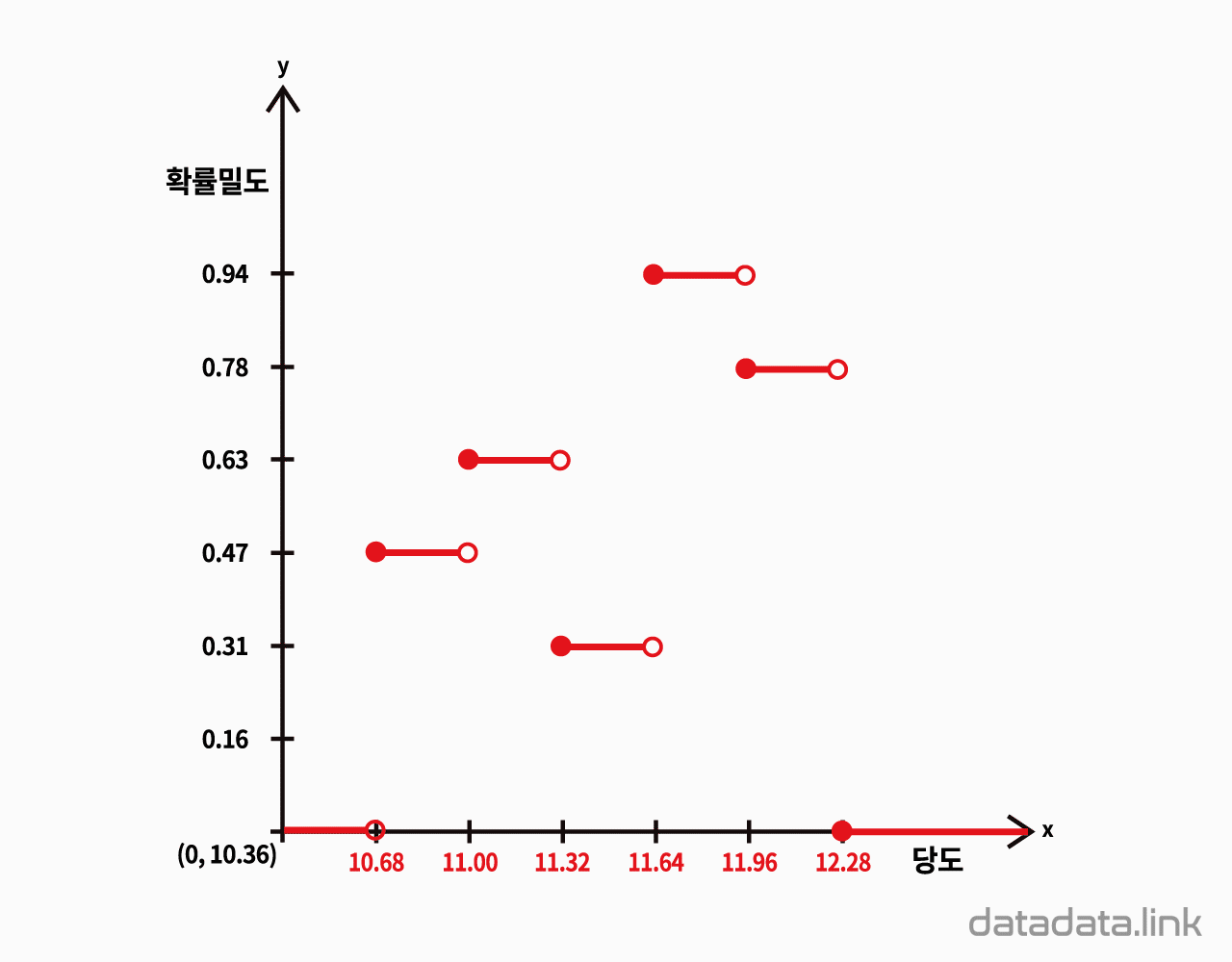
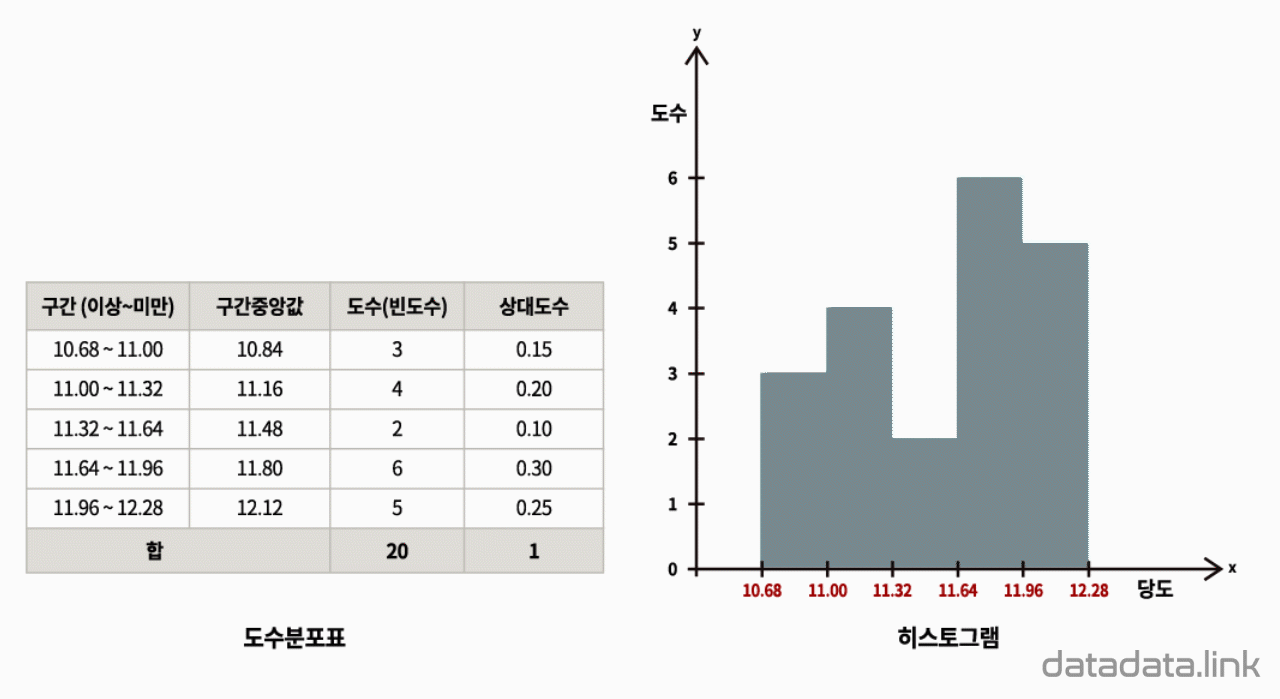
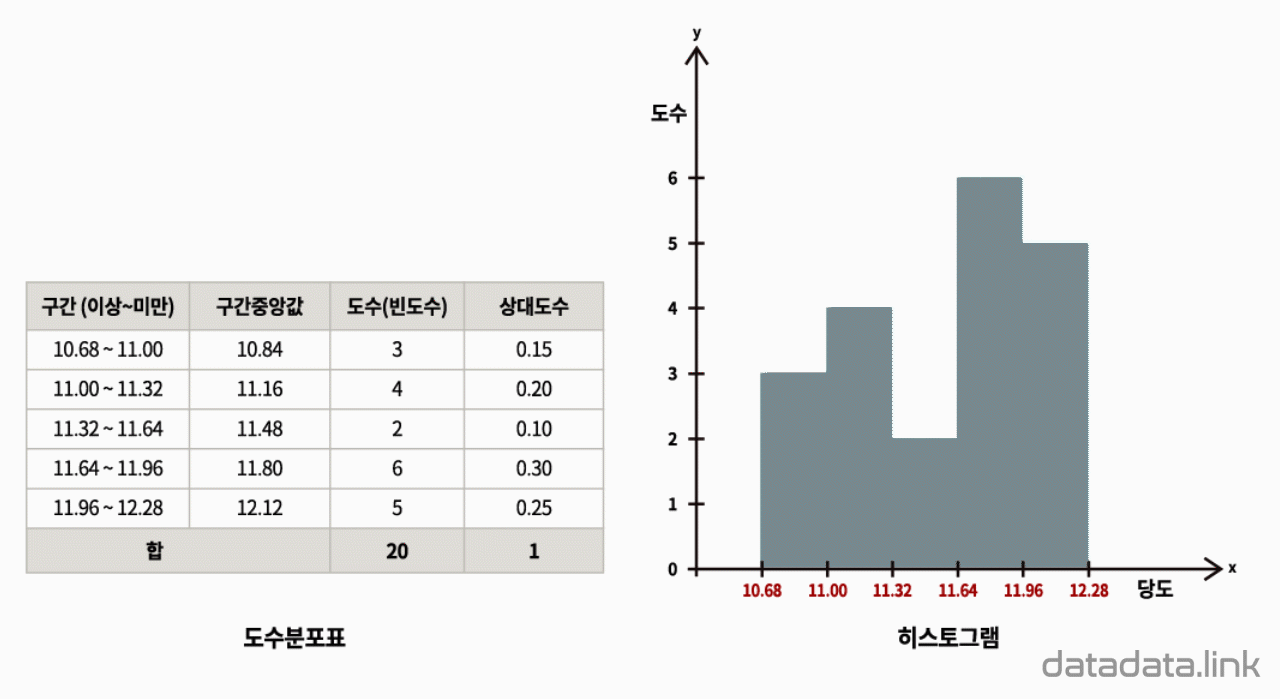
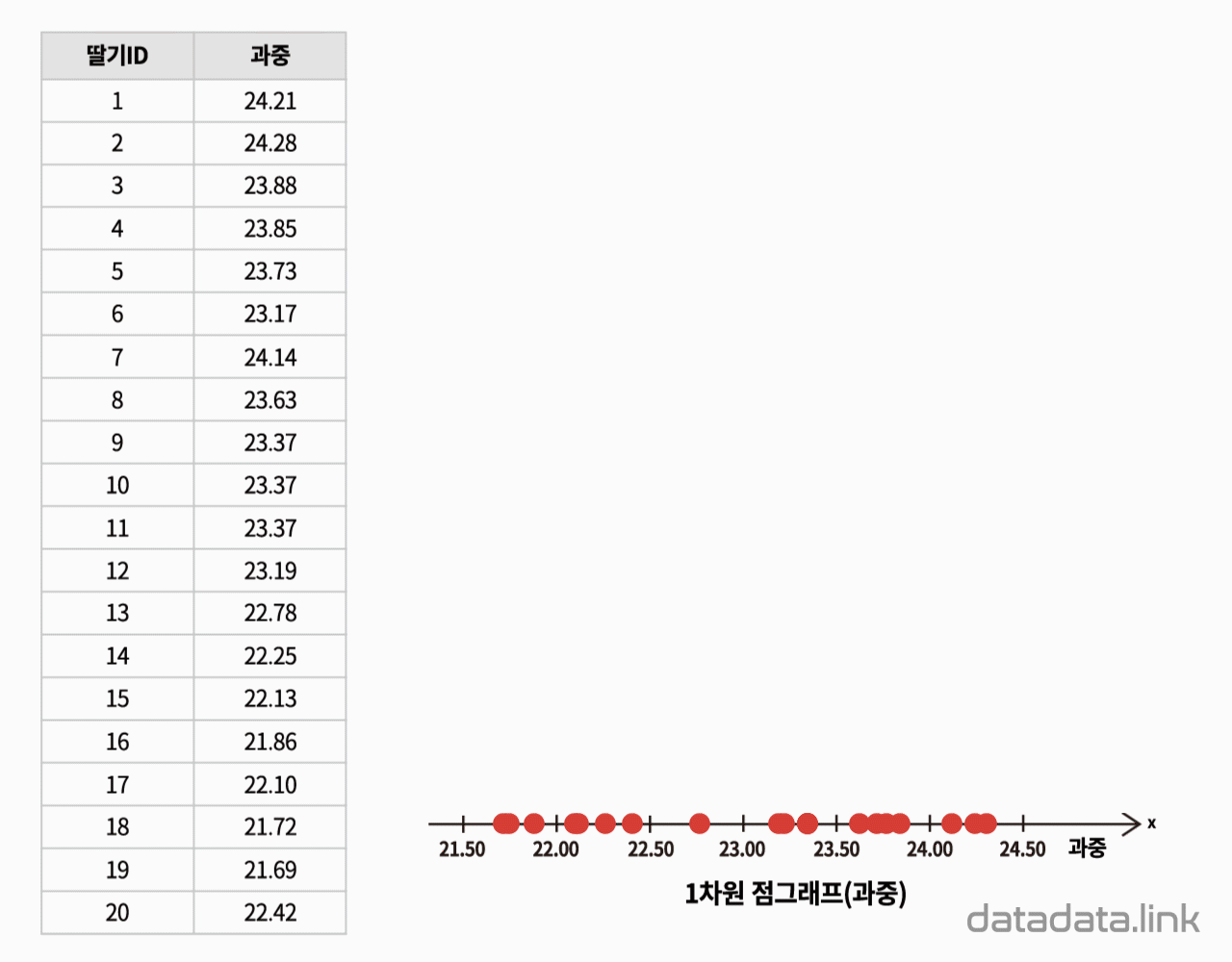
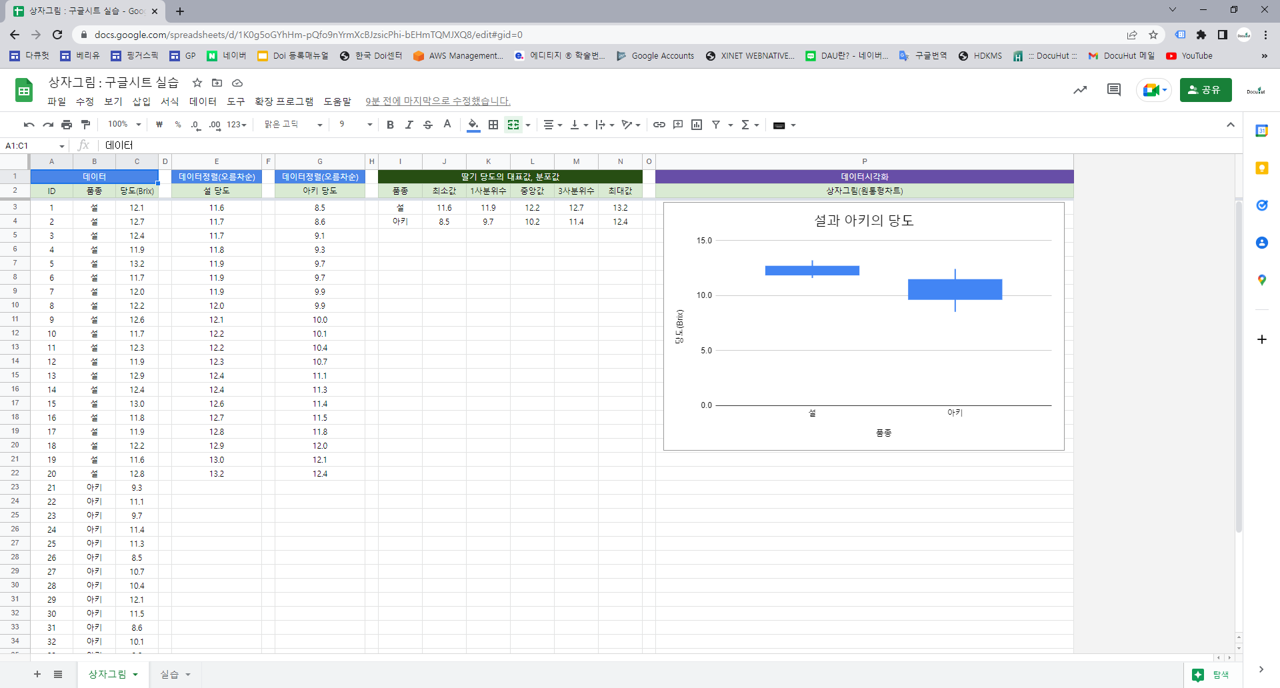
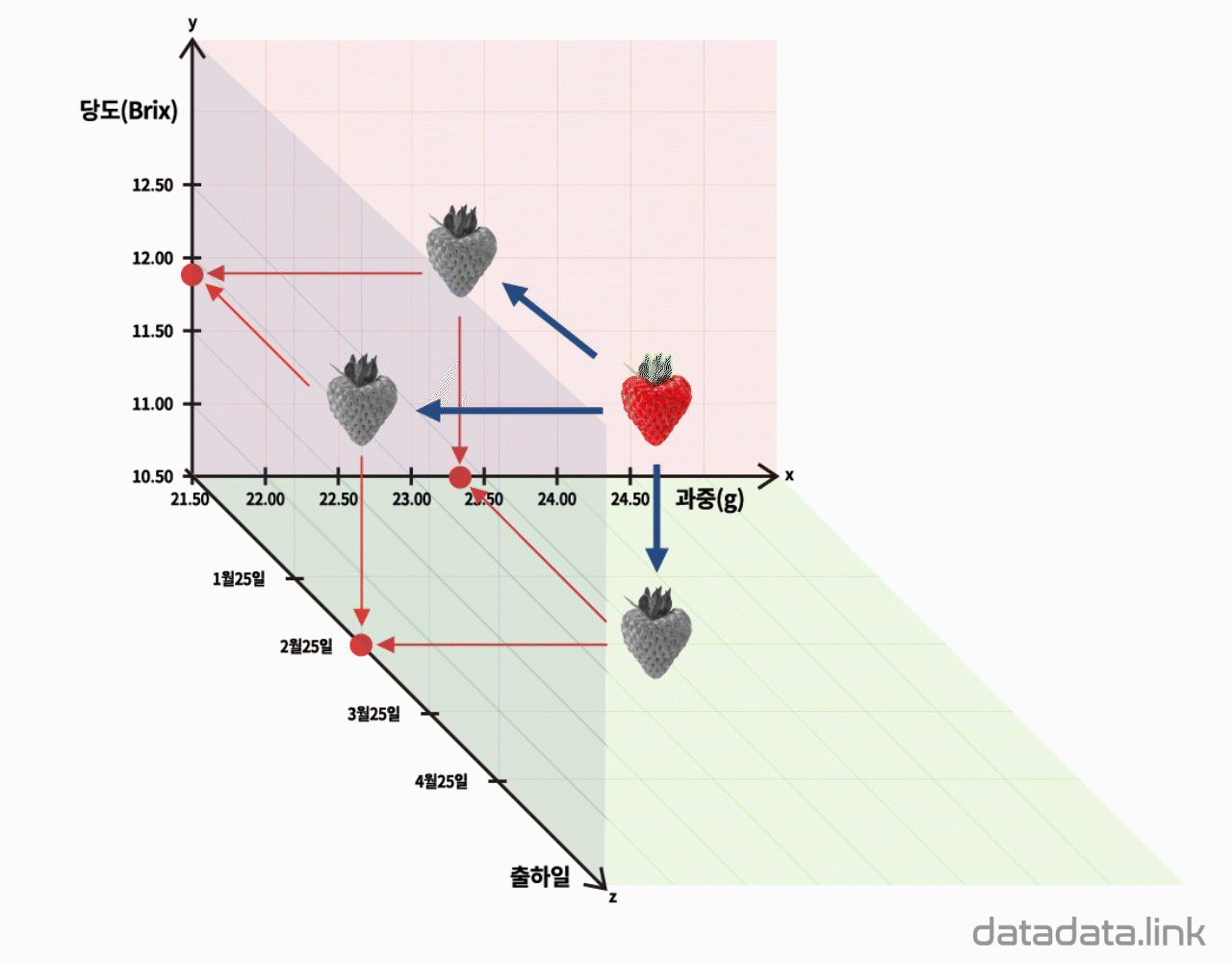
20개의 딸기의 과중과 당도를 측정한 데이터가 있습니다. 데이터를 보면 딸기 하나에 과중과 당도, 두 개의 데이터(변수값)가 있습니다. 딸기의 과중과 당도의 관계를 탐색하기 위하여 두 변수의 관계를 시각화하는 산점도(scatter plot)를 그립니다.
딸기 하나를 한 점(point)으로 생각하고 딸기 하나가 독립된 두 변수를 가진다면, 2차원 직각 좌표계에 점으로 딸기를 나타낼 수 있습니다. 결과적으로 딸기가 20개이므로 20개의 점이 평면좌표계에 찍힙니다. 산점도를 그릴 때는 보통, 원인이 되는 변수를 $X$축(가로축), 결과를 나타내는 변수를 $Y$축(세로축)으로 정합니다. 따라서 과중과 당도를 각각 $X$축과 $Y$축에 나타냅니다.
애니메이션의 산점도를 보면 과중이 클수록 당도가 높게 나옵니다. 딸기가 무거울수록, 즉, 큰 딸기일수록 달다고 해석할 수 있겠습니다. 두번째 애니메이션에서는 20개 딸기의 출하일과 당도를 기록한 데이터를 다룹니다. 산점도를 보면 출하일이 겨울에 가까울수록 딸기가 달다는 것을 알 수 있습니다.
산점도는 데이터의 요소가 가지는 두 변수의 상관 관계를 분석하는 그래프입니다. 특히, 두 연속형 변수의 관계를 분석하는데 매우 효율적입니다. 2차원 산점도는 개체(object, 요소, element)의 한 변수를 $X$축, 다른 변수를 $Y$축으로 하여 각각의 관찰값을 $XY$ 평면상의 점으로 나타내는 “데이터시각화”입니다.
두 개의 변수에서 한쪽이 증가하면 다른 쪽도 증가하는 관계를 양의 상관이라고 합니다. 반대로 한쪽이 증가하면 다른 쪽은 줄어드는 관계를 음의 상관이라고 합니다.
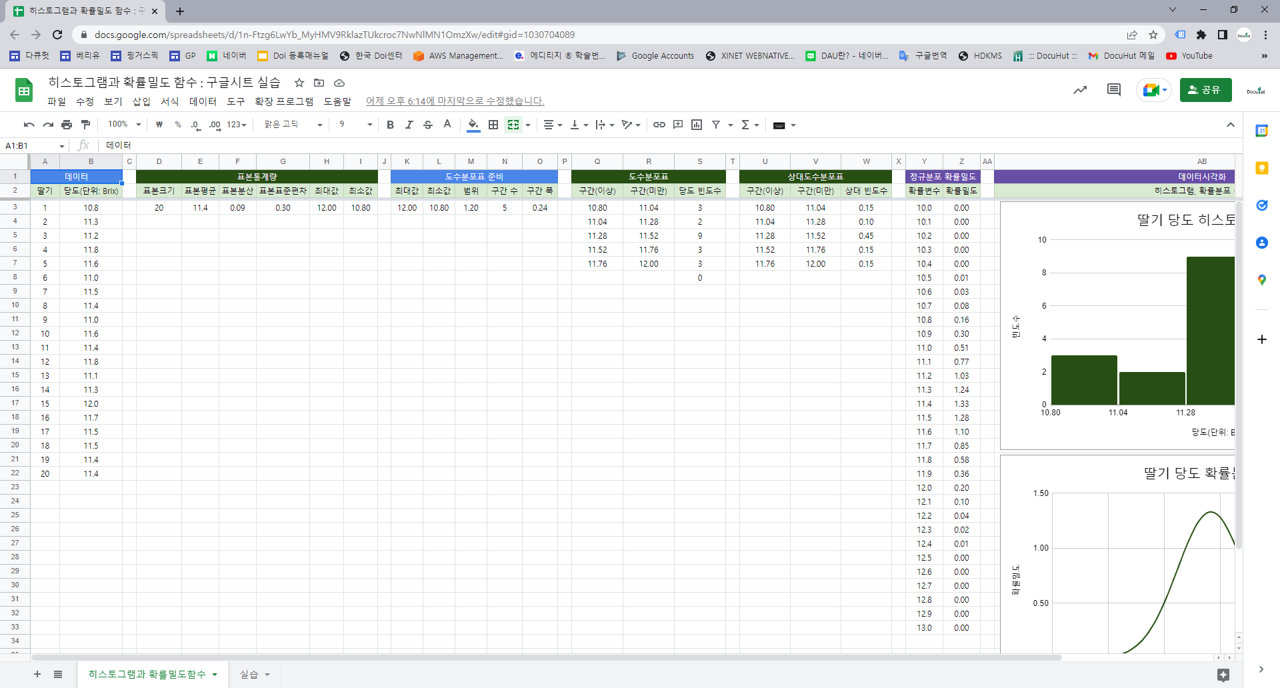
3. 실습
3.2. 구글시트 함수
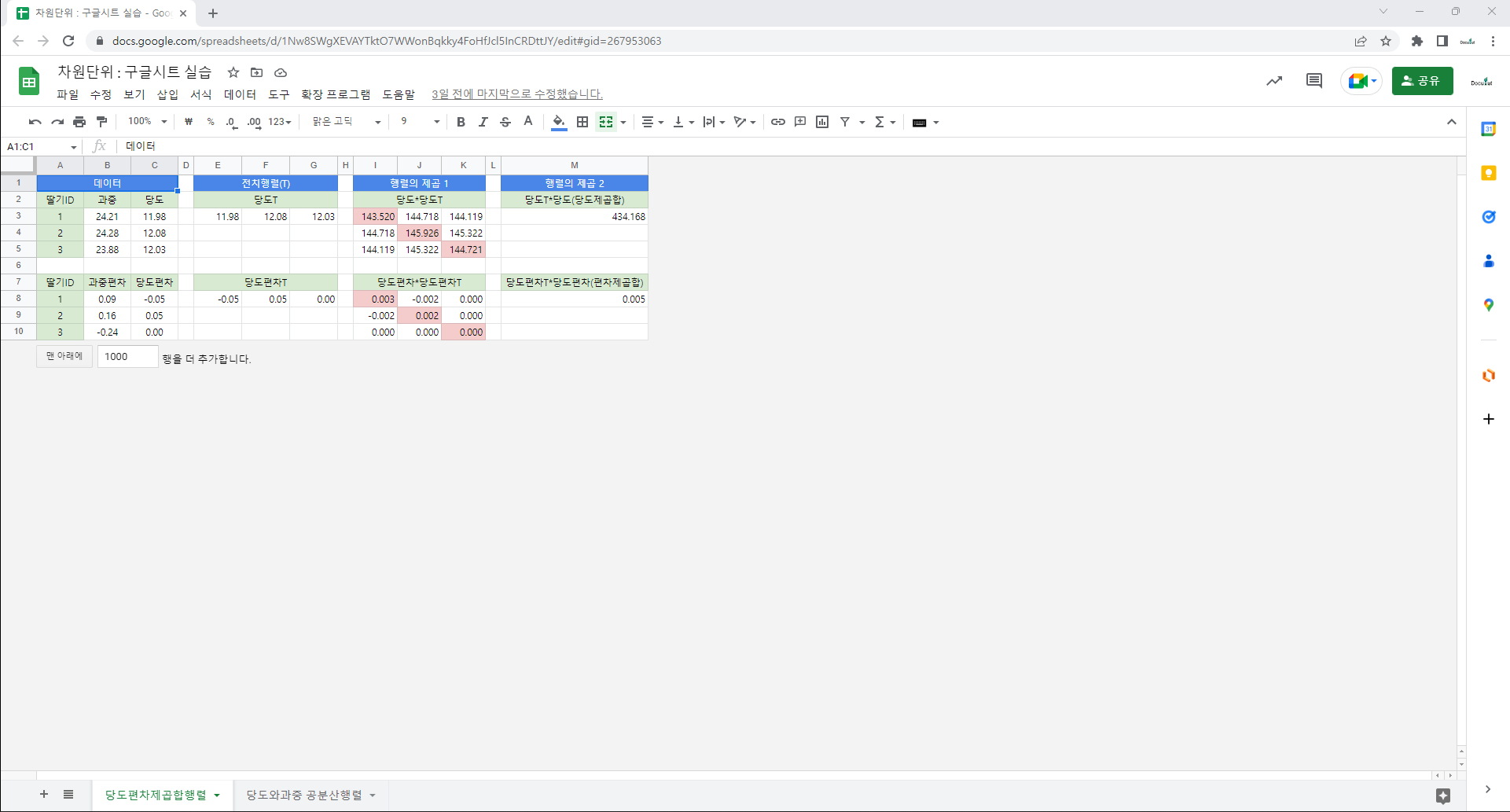
=AVERAGE(B3:B22) : 평균. B3에서 B22에 있는 데이터의 평균을 구함. 데이터를 모두 더해서 개수로 나눔. 산술평균.
3.3. 실습강의
– 데이터
– 산점도
– 세로축 범위 조정
– 실습 안내
4. 용어
4.1. 용어
산점도
산점도(산포도)는 일반적으로 여러 변수를 가지는 개체를 표시하기 위해 직각 좌표계를 사용하는 그래프 유형입니다. 점이 시각적으로 정의된 경우 (색상 / 모양 / 크기) 하나의 추가 변수로 표시 될 수 있습니다. 3차원 산점도에서 데이터는 수평 축상의 위치를 결정하는 하나의 변수 값과 수직축 상의 위치를 결정하는 다른 변수의 값을 갖는 점들의 모음으로 표시됩니다.