자연상수 e

곱의 기준은 1입니다.

1은 자신을 x번 곱해도 자신이 됩니다. 

1 × 1 × 1… = 1^x = 1

그리고 모든 수는 0번 곱하면  1이 됩니다.

a⁰ = 1

그렇다면 자신을 곱해서 나오는 값을 자신이 증가하는 비율로 가지는 자신의 수가 있다면 무엇일까요?

바로 자연상수 $e$입니다

e = 2.718… 인 무리수입니다.

지수함수 e^x

e를 x번 곱해서 나오는 함수 ⇒ e × e × e…  ⇒ $e^x = y $

${dy\over dx} = e^x = y$

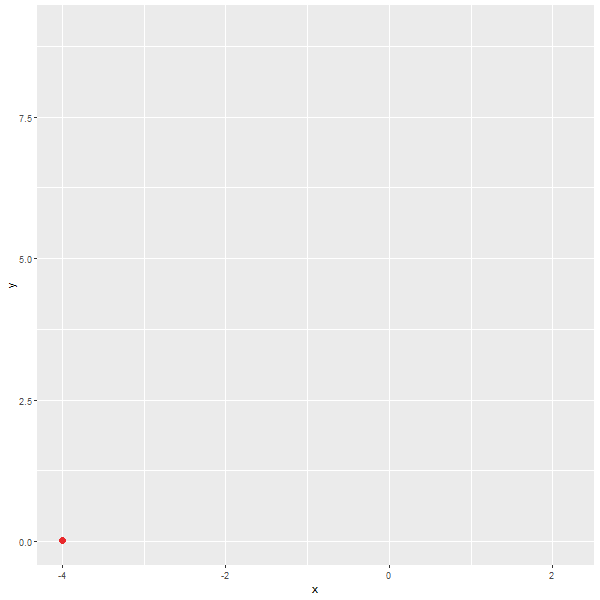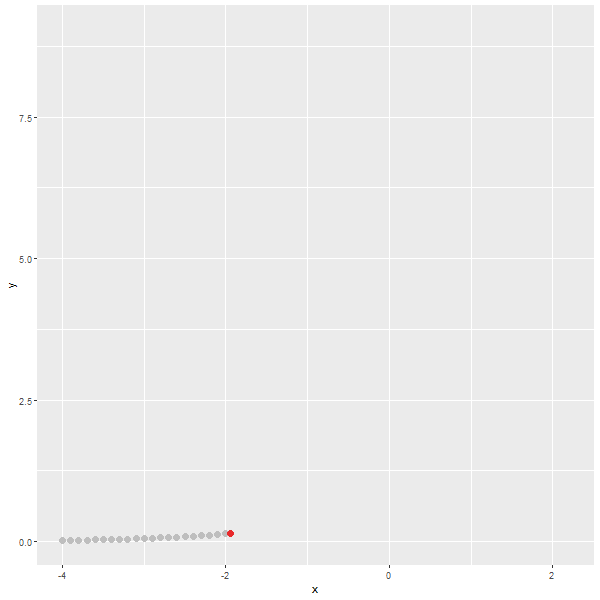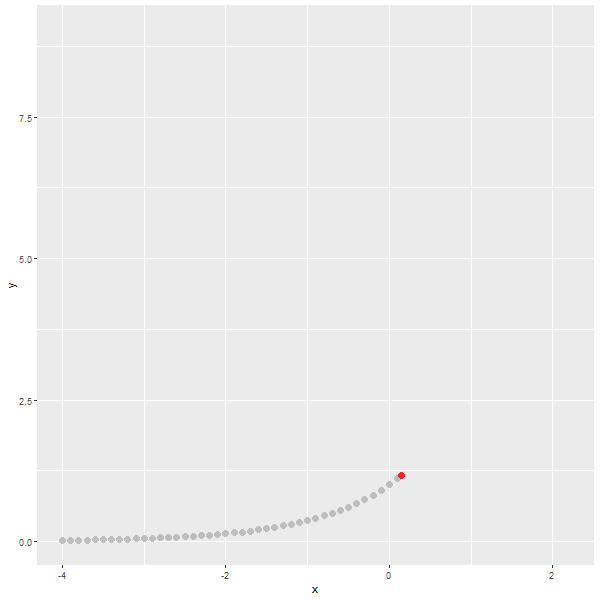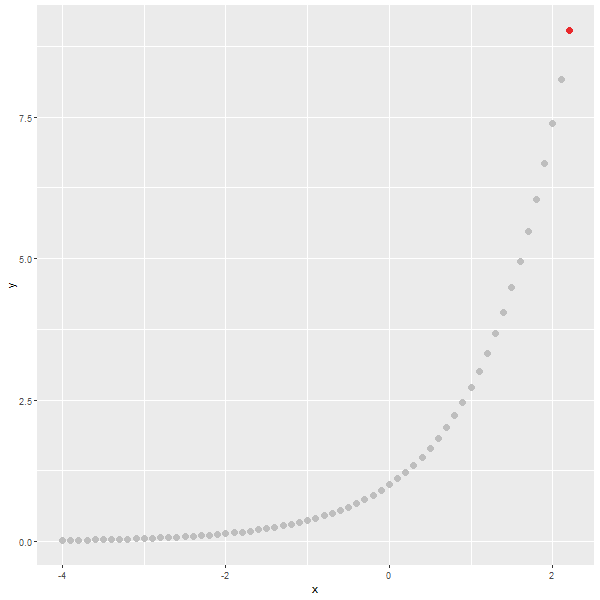
자연상수가 밑이 되는 지수함수를 살펴보면

$y=e^x$

x < 0 :

$y=(1/e)^{ㅣxㅣ}$

x = 0 :

$y=e^x= 1$

 x =1 :

$y=e^x = e $

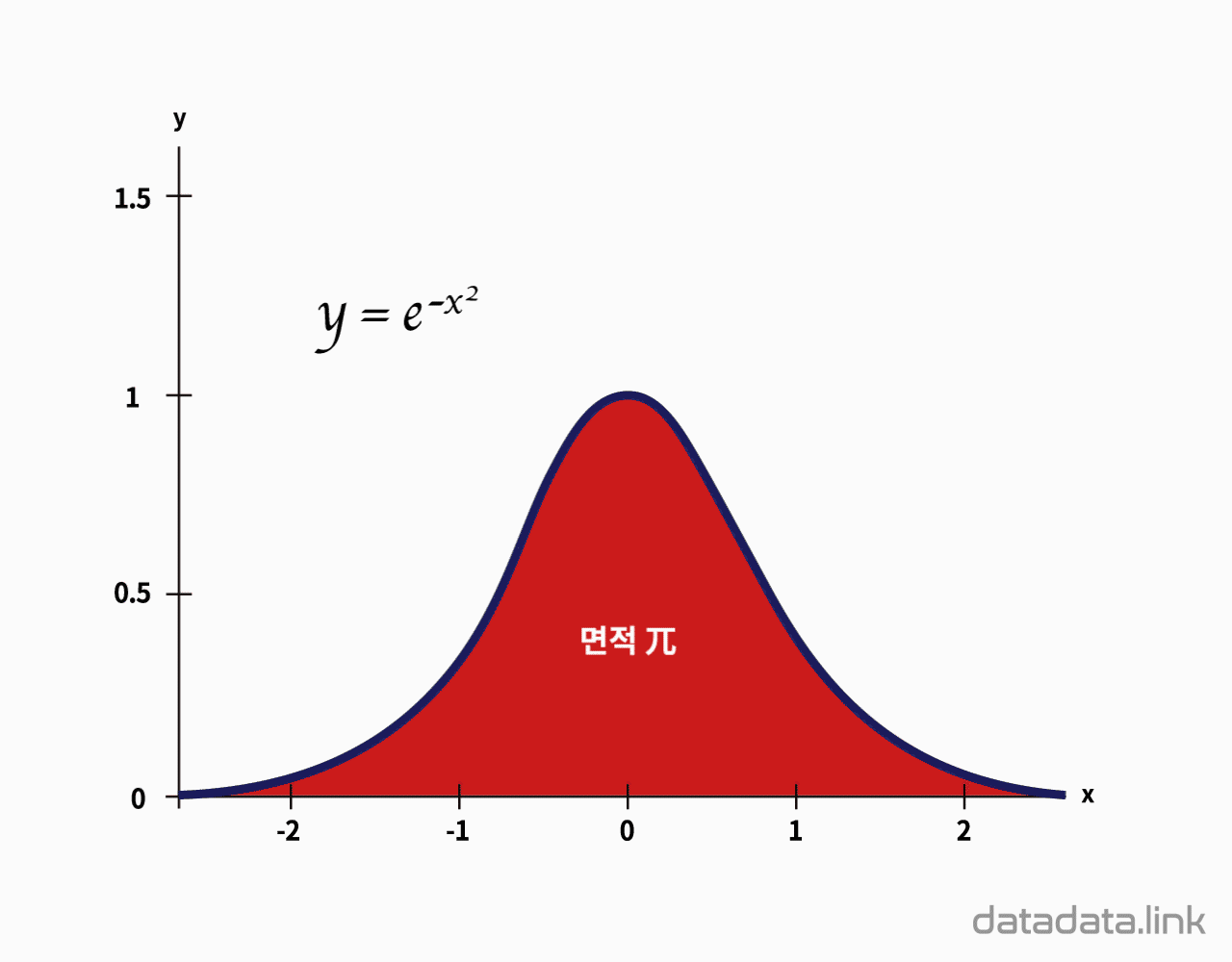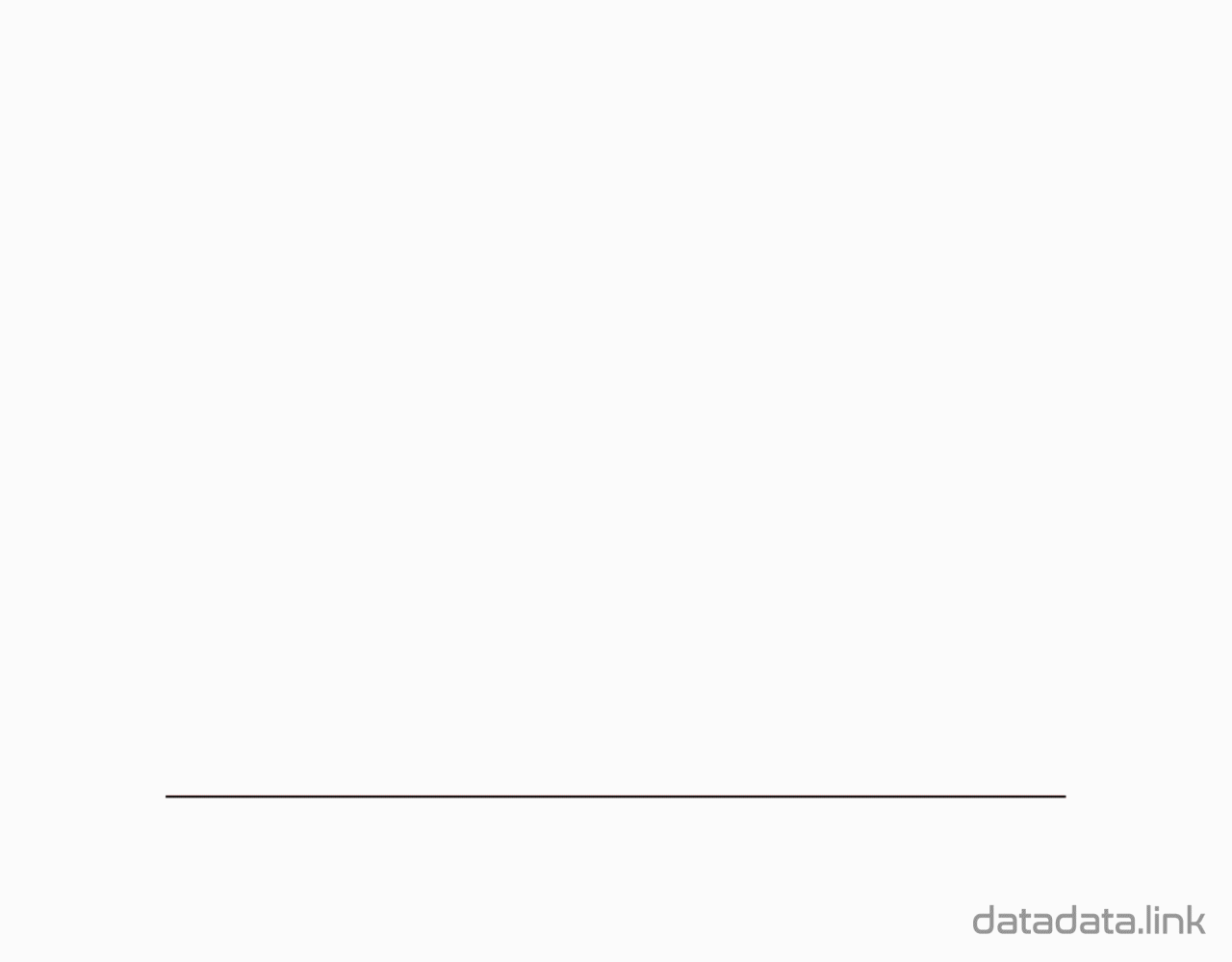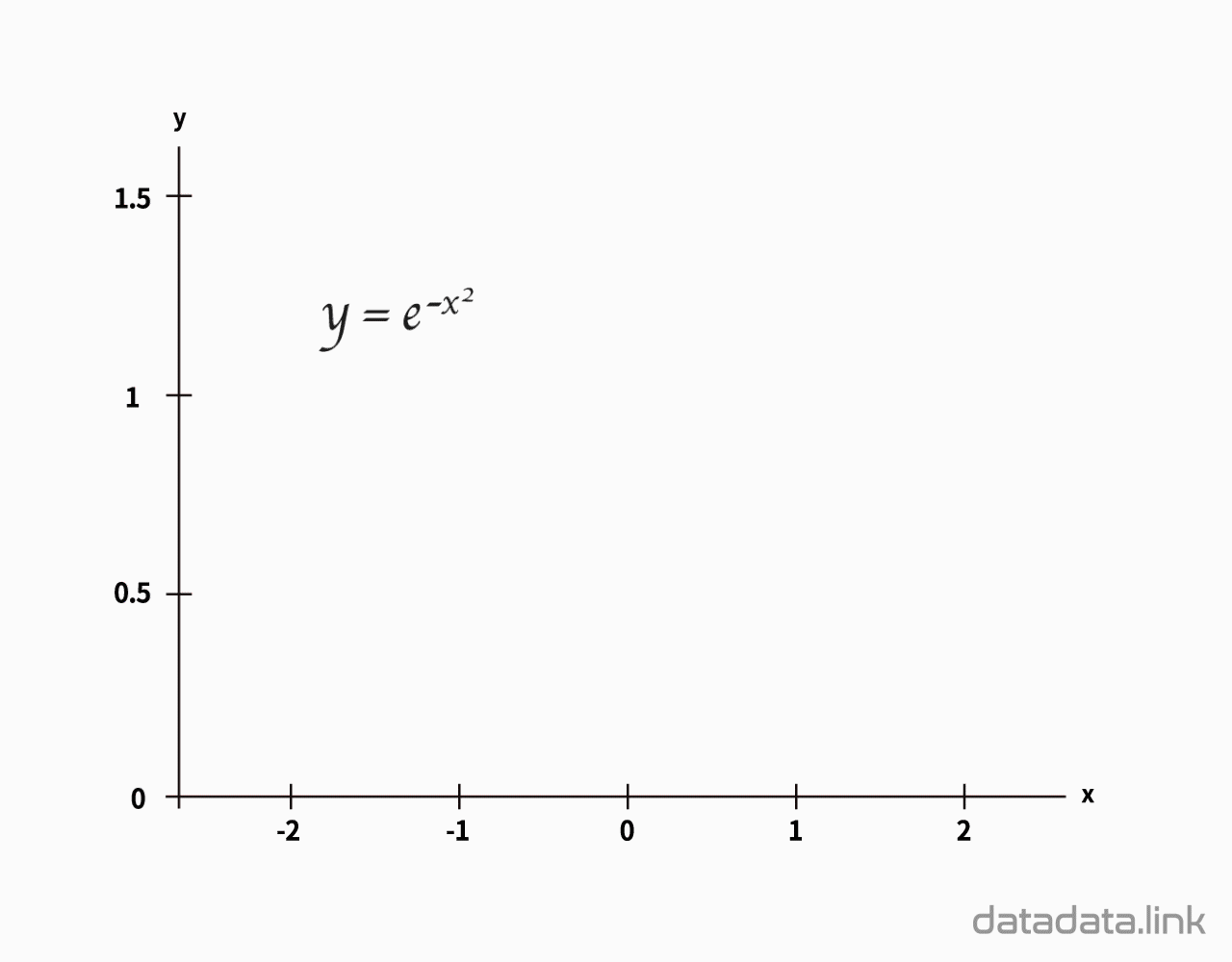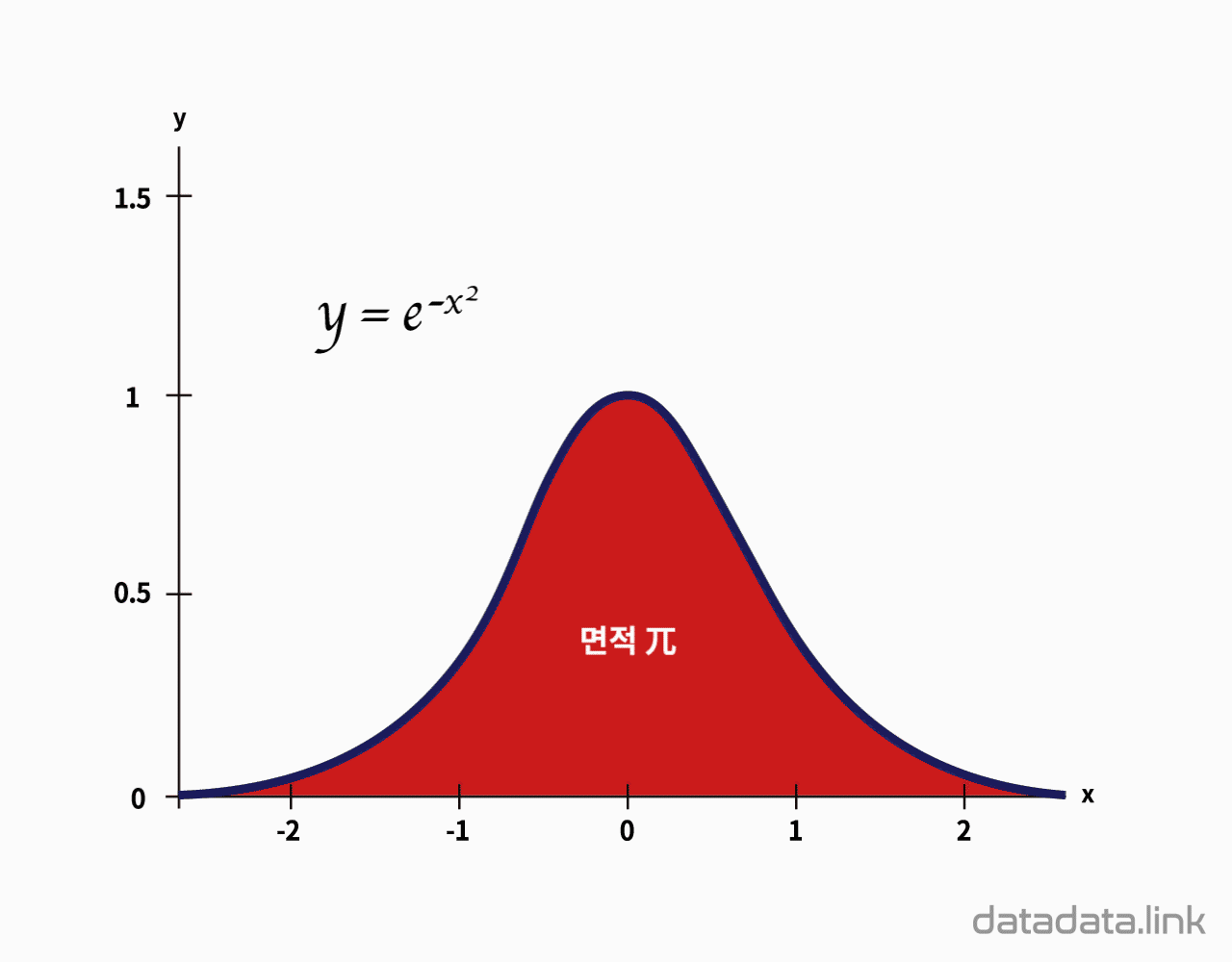
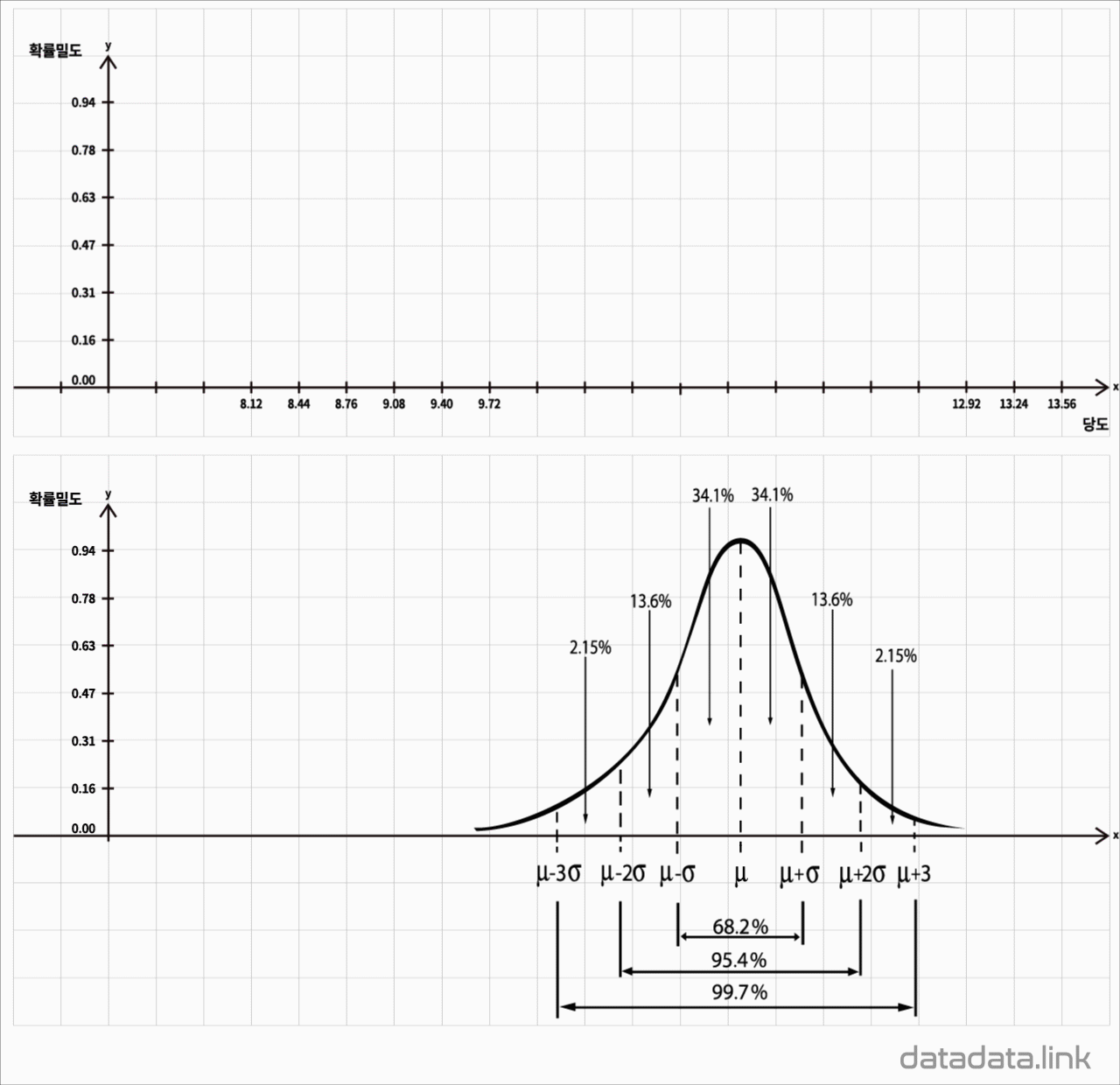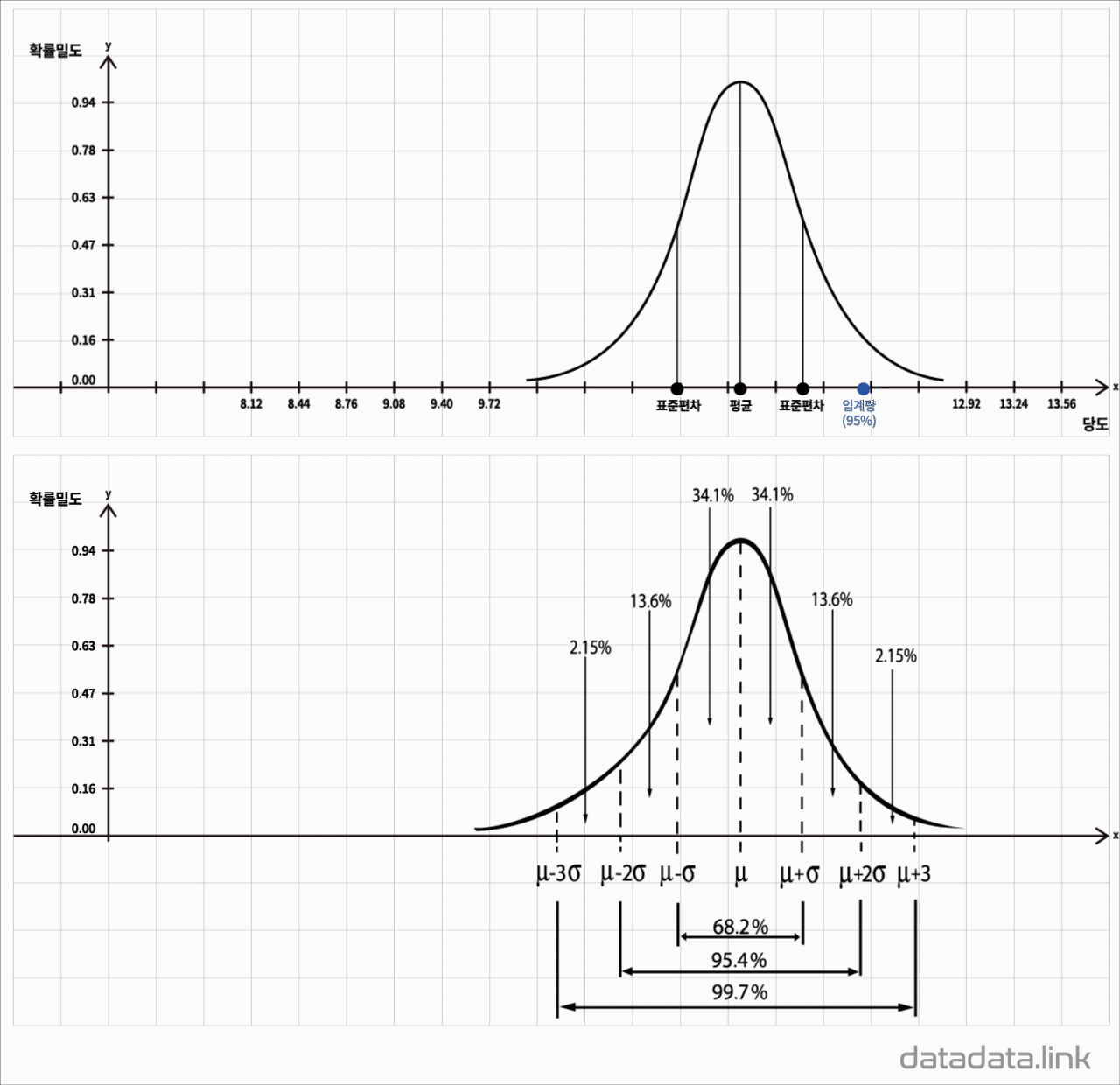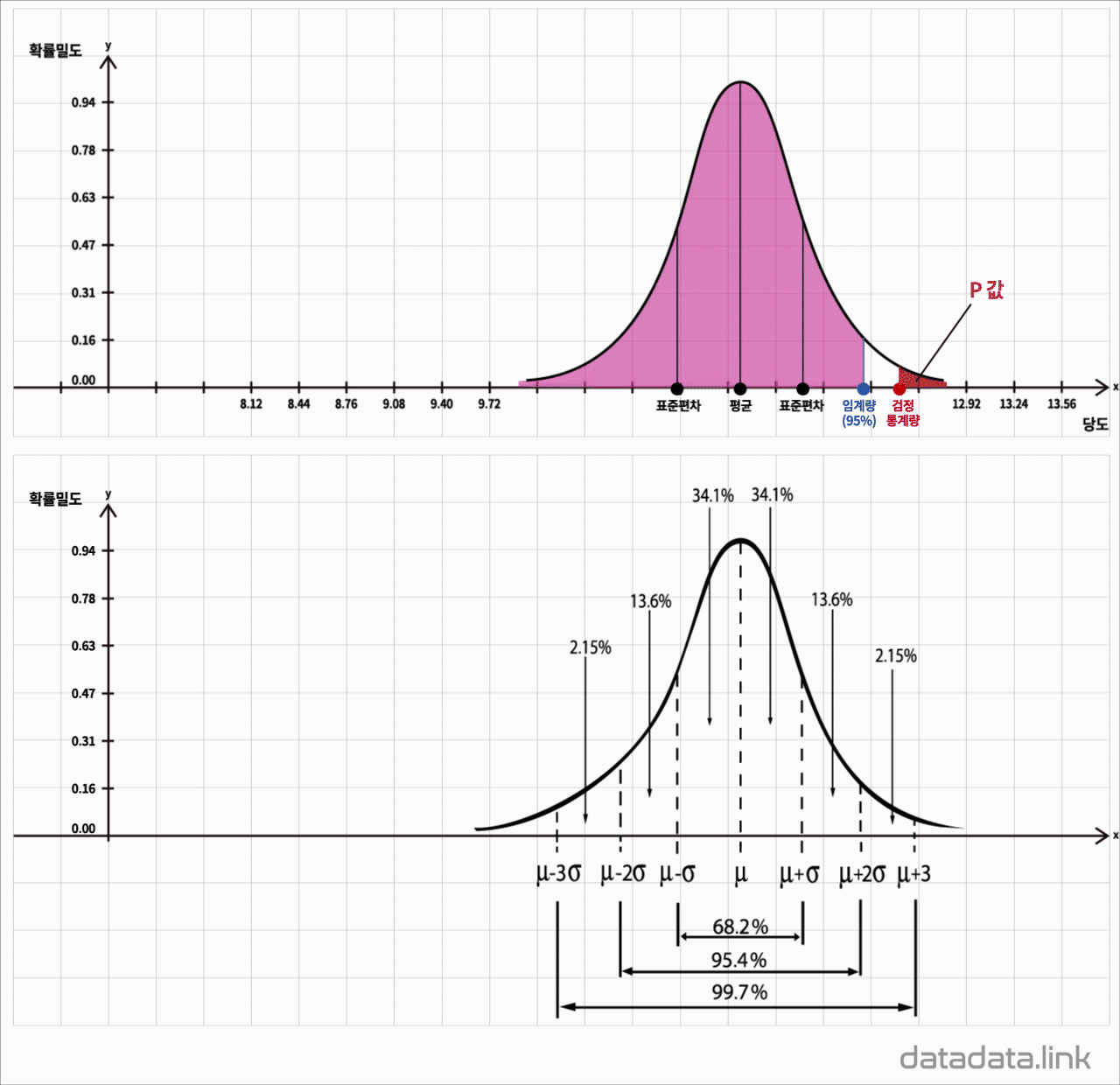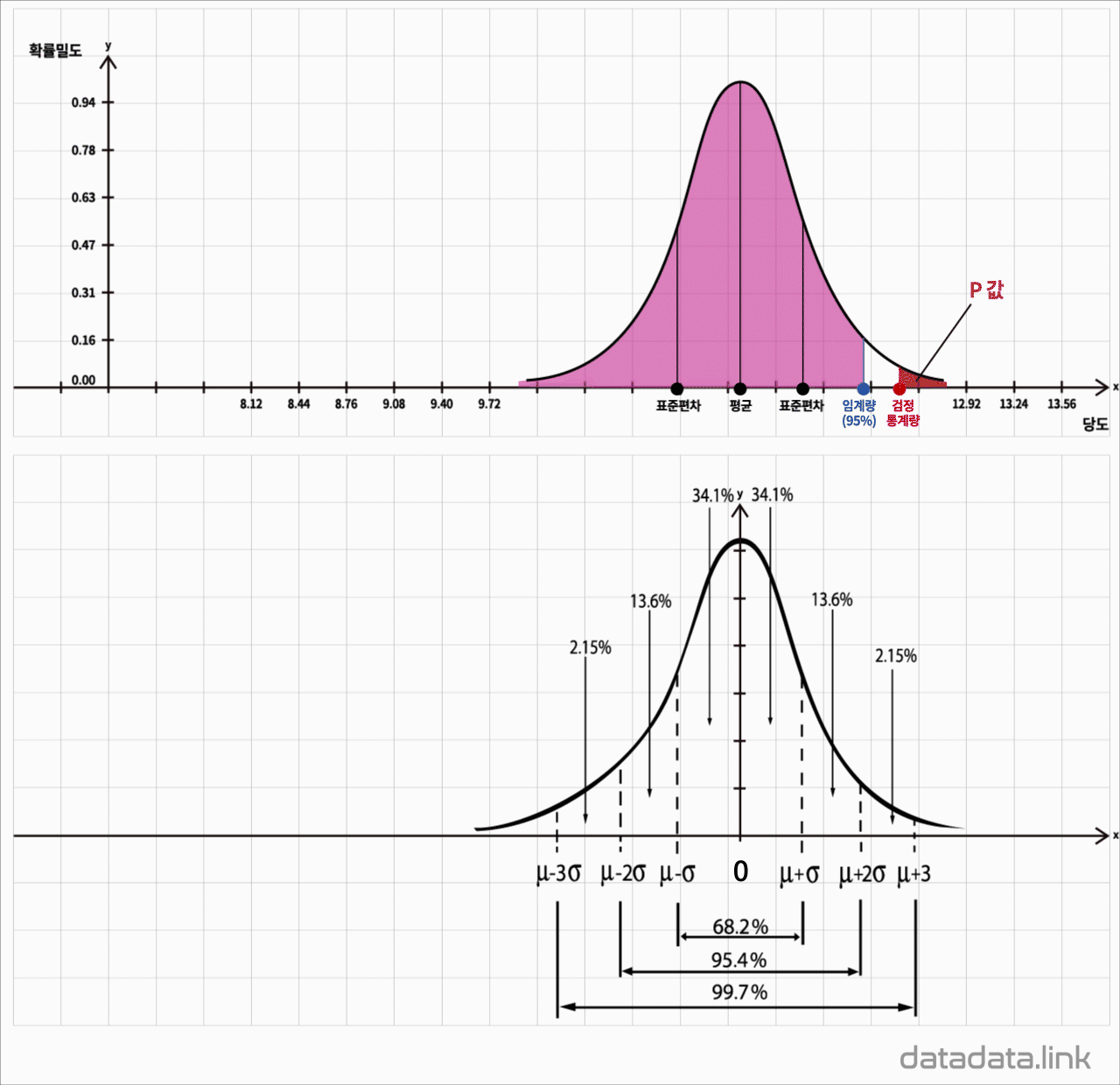
정규분포

표준정규분포

$$y=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$$

평균 $\mu$와 분산 $\sigma^{2}$ 를 모수로 하고 정규분포를 가지는 모집단의  확률밀도함수

$$f(X)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\ -\infty\leq X\leq+\infty$$