Central limit theorem ?
중심극한정리 ?
1.1. 중심극한정리
4.1. 용어
1. 애니메이션
2. 설명
2.1. 중심극한정리
중심극한정리(Central Limit Theorem)는 표본들의 평균을 구하는 과정에서 극단적인 값들이 서로 상쇄되어 표본들의 평균은 모집단의 평균으로 모이는 경향을 말합니다.
평균 $\mu$, 분산 $\sigma^2$인 모집단에서 크기가 $n$인 선택가능한 모든 표본을 뽑습니다.
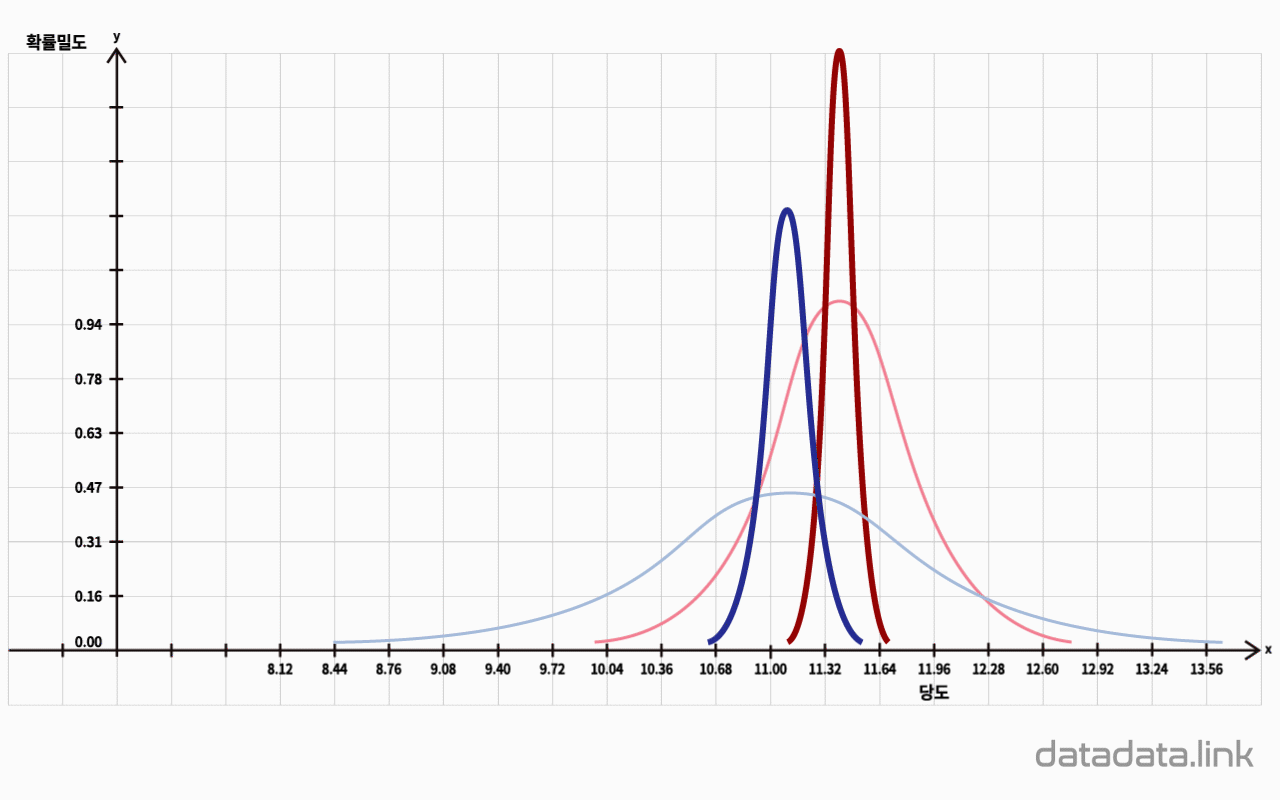
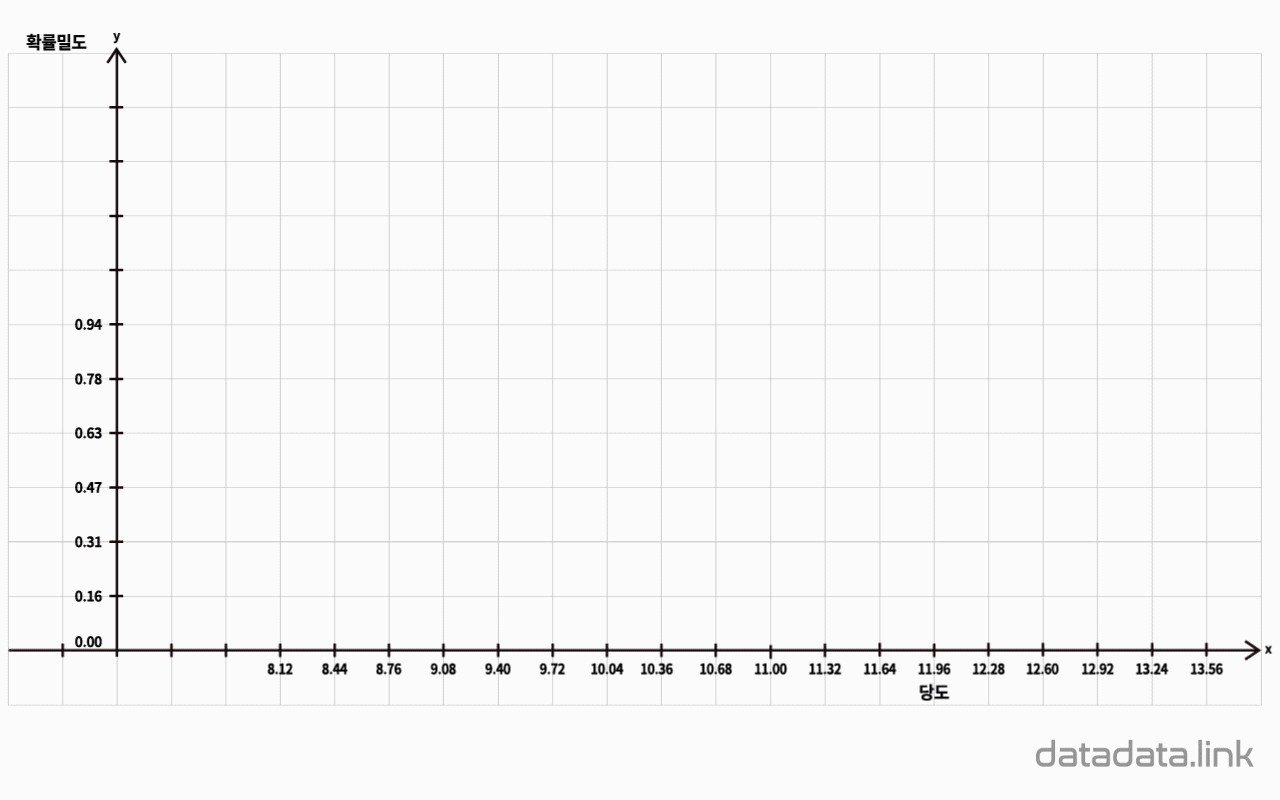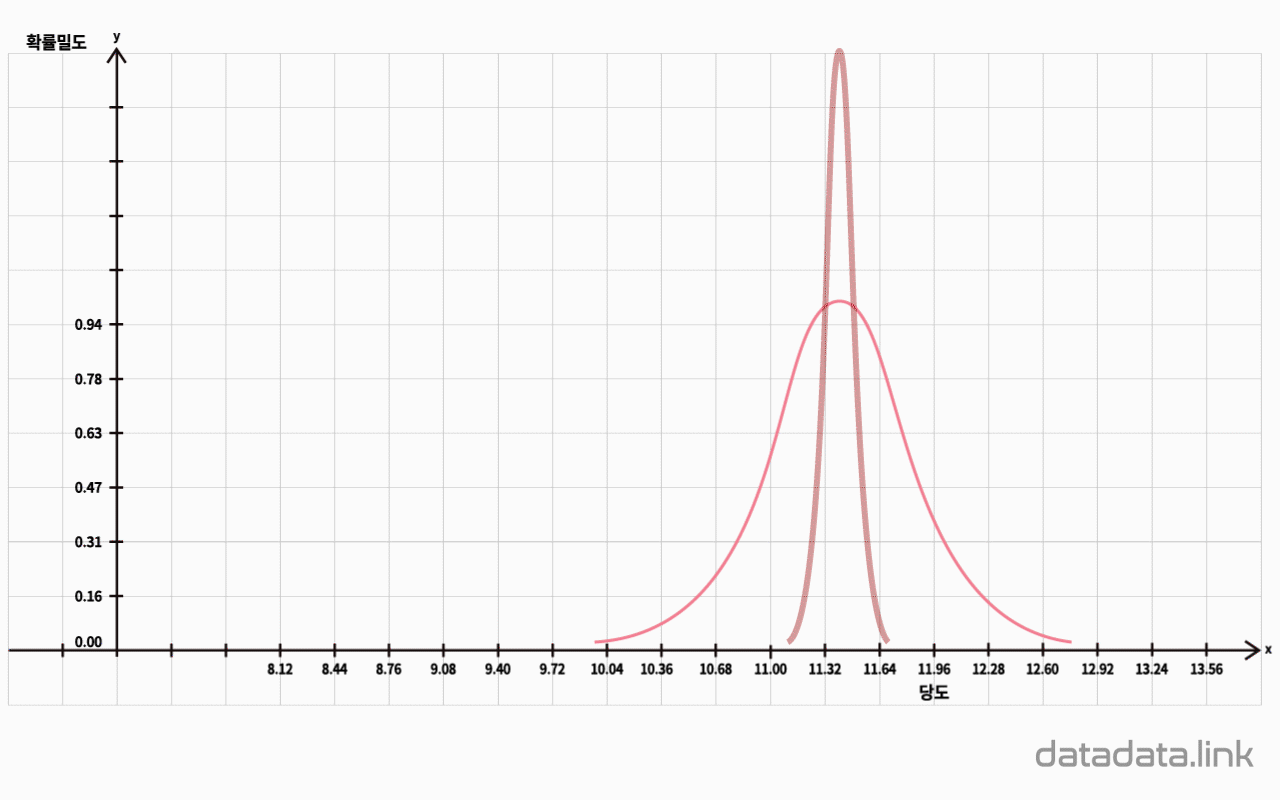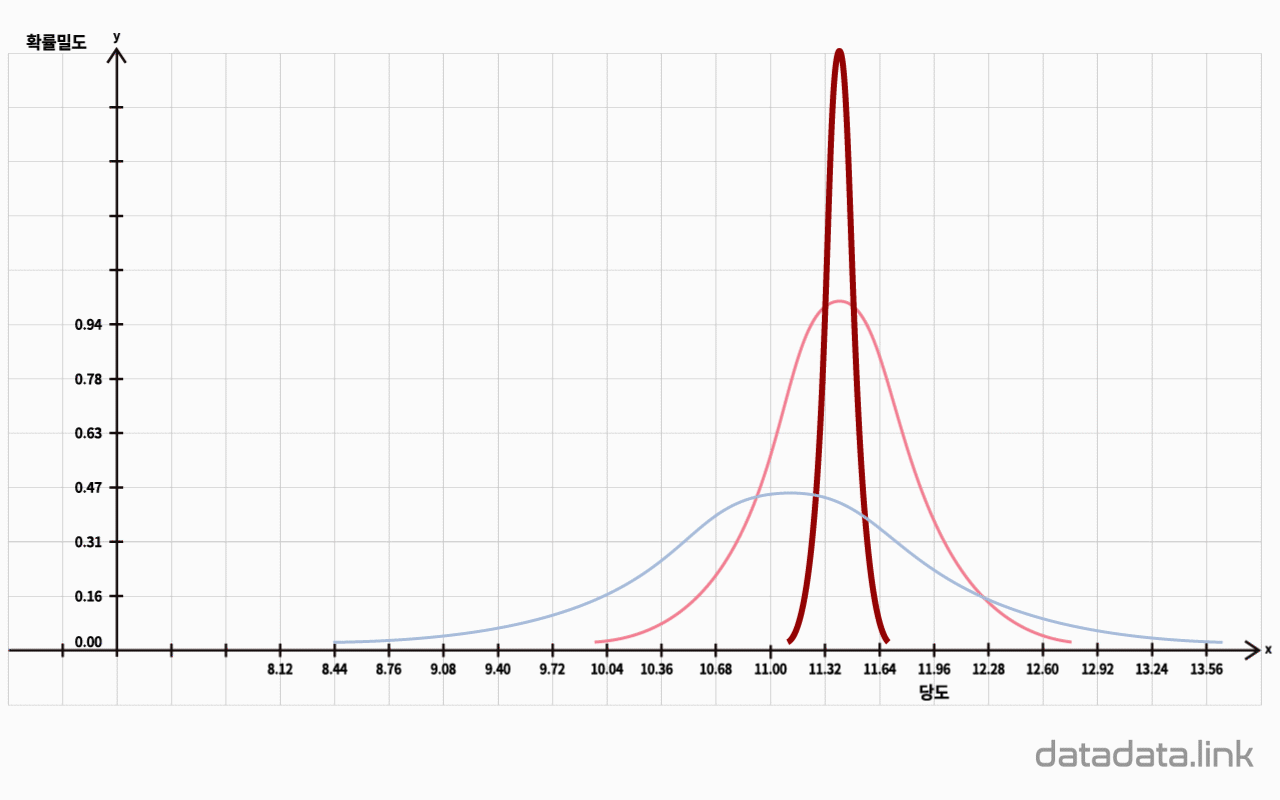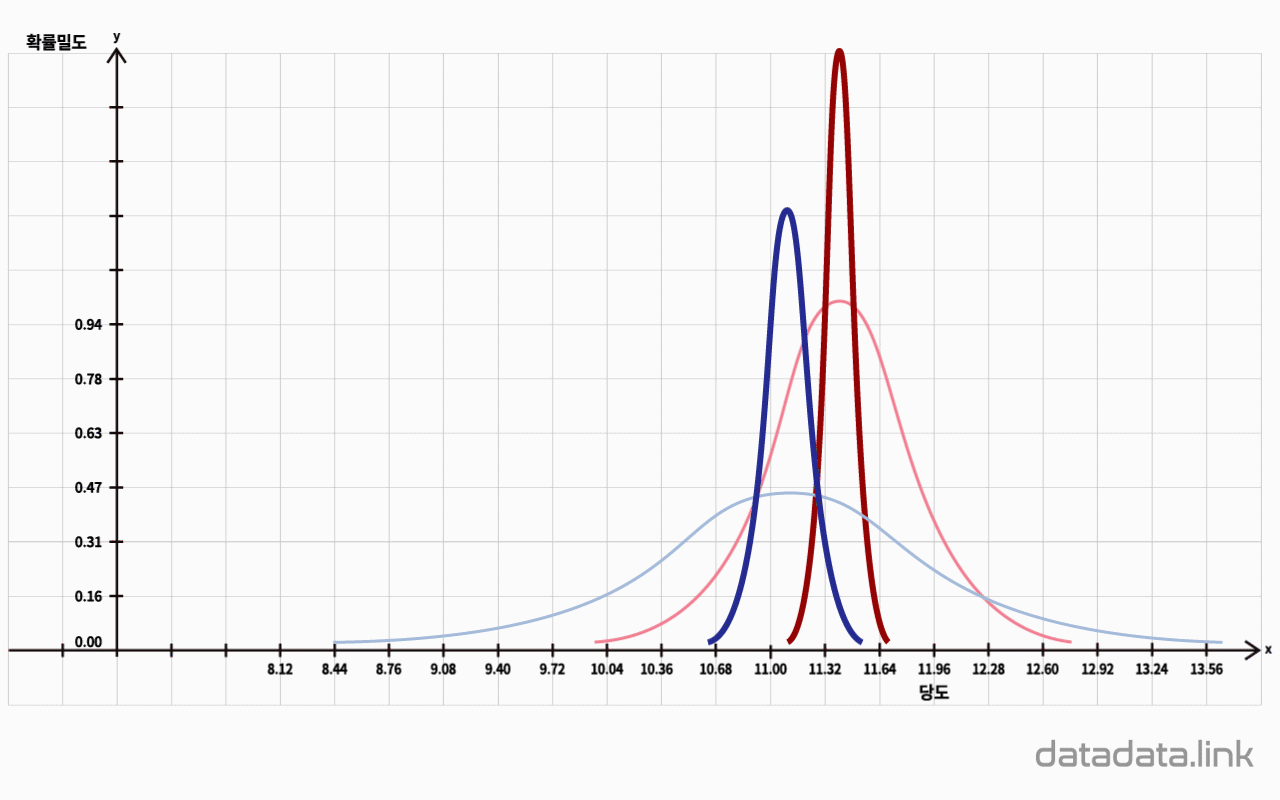
그럴때 모집단의 분포모양과는 상관없이 표본평균들의 분포는 $n$을 증가시킬수록 정규분포에 접근합니다.
중심극한정리를 다시 표현하면, 표본평균들의 분포는 모집단평균을 중심으로 정규분포를 이룬다는 정리입니다.
표본의 크기 $n$의 값이 크면 표본평균들의 분산은 작아집니다.
표본평균들의 분산은 모집단의 분산을 표본의 크기로 나눈 값이기 때문입니다.
표본평균들의 평균은 표본의 개수가 많아질 수록 모평균에 가까워 집니다.
2.2. 모수(parameter)와 추정량(estimator)
모평균은 하나의 값이지만 표본평균은 여러 개의 값을 가질 수 있습니다. 즉, 모평균 $\mu$는 모집단의 하나의 대표값인 모수(parameter)라고 부르고 표본평균은 서로 다른 많은 값을 가질 수 있는 확률변수로서 일반적으로 대문자를 사용하여 $\bar{X}$로 표시합니다.
$\bar{X}$는 모수 $\mu$를 추정하는 하나의 추정량(estimator)입니다.
한 표본에서 구한 $\bar{X}$의 관측값을 소문자를 사용하여 $\bar{x}$로 표시하고 이 $\bar{x}$는 $\mu$의 추정값(estimate)입니다.
모집단의 분산 $\sigma^2$를 추정하는 추정량은 표본분산 $S^2$이고 그 관측값은 $s^2$으로 표시합니다.
만일 모집단이 정규분포 $N(\mu,\sigma^2)$라면 표본평균의 표집분포는 정확히 정규분포 $N(\mu,\sigma^2/n)$입니다.
만일 모집단이 평균이 $\mu$이고 분산이 $\sigma^2$인 무한개의 원소를 가지는 모집단이라면 표본의 크기($n$)가 충분히 클 때 모집단이 어떠한 분포를 가지더라도 표본평균의 표집분포는 근사적으로 정규분포 $N(\mu,\sigma^2/n)$입니다.
이를 중심극한정리(Central Limit Theorem)라고 하는데 구체적으로 요약하면 다음과 같습니다.
3. 실습
3.3. 실습강의
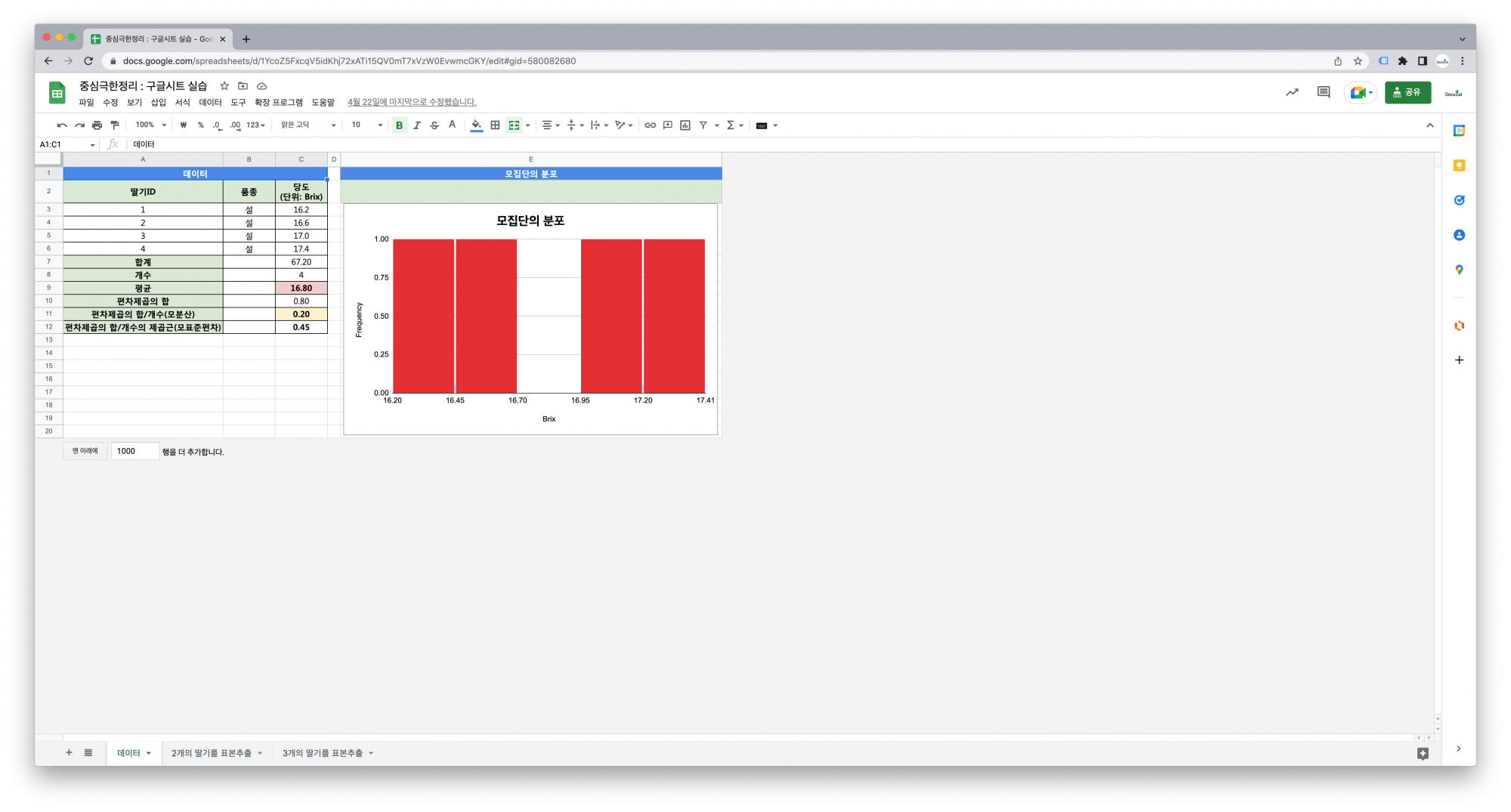
데이터
데이터 요약
표본 크기가 2인 표본들의 평균
표본 크기가 3인 표본들의 평균
중심극한정리
4. 용어와 수식
4.1 용어
중심극한정리(Central Limit Theorem)
모집단이 평균 $\mu$, 분산 $\sigma^2$인 정규분포가 아닌 임의의 분포일 때 크기가 $n$인 표본을 단순임의 복원추출하면 표본평균들의 분포는 다음과 같은 특성을 갖습니다.
1) 모든 가능한 표본평균들의 평균(${\mu}_{\bar{x}}$)은 모평균과 같다. ($\mu_\bar{x}=\mu$)
2) 모든 가능한 표본평균들의 분산($\sigma_{\bar{X}}$)은 모분산을 $n$으로 나눈 값이다. (${\mathit{\sigma}}_{\bar{X}}^{2}{=}\dfrac{{\mathit{\sigma}}^{2}}{n}$)
3) 모든 가능한 표본평균들의 분포는 근사적으로 정규분포이다.
위의 사실을 간단히 ${X}\sim{N}\left({\mathit{\mu}{,}\dfrac{{\mathit{\sigma}}^{2}}{n}}\right)$로 적기도 한다.
중심극한정리는 현대통계학의 기본이 되는 이론으로 매우 중요한 정리입이다.