표본과 모집단의 통계량 비교
1. 애니메이션
2. 설명
2.1 모집단통계량
통계량을 의미하는 Statistic의 복수형인 Statistics는 통계를 의미합니다.
통계량이 모이면 통계가 된다는 뜻이겠지요.
통계량에는 우리가 잘 아는 평균이 있습니다.
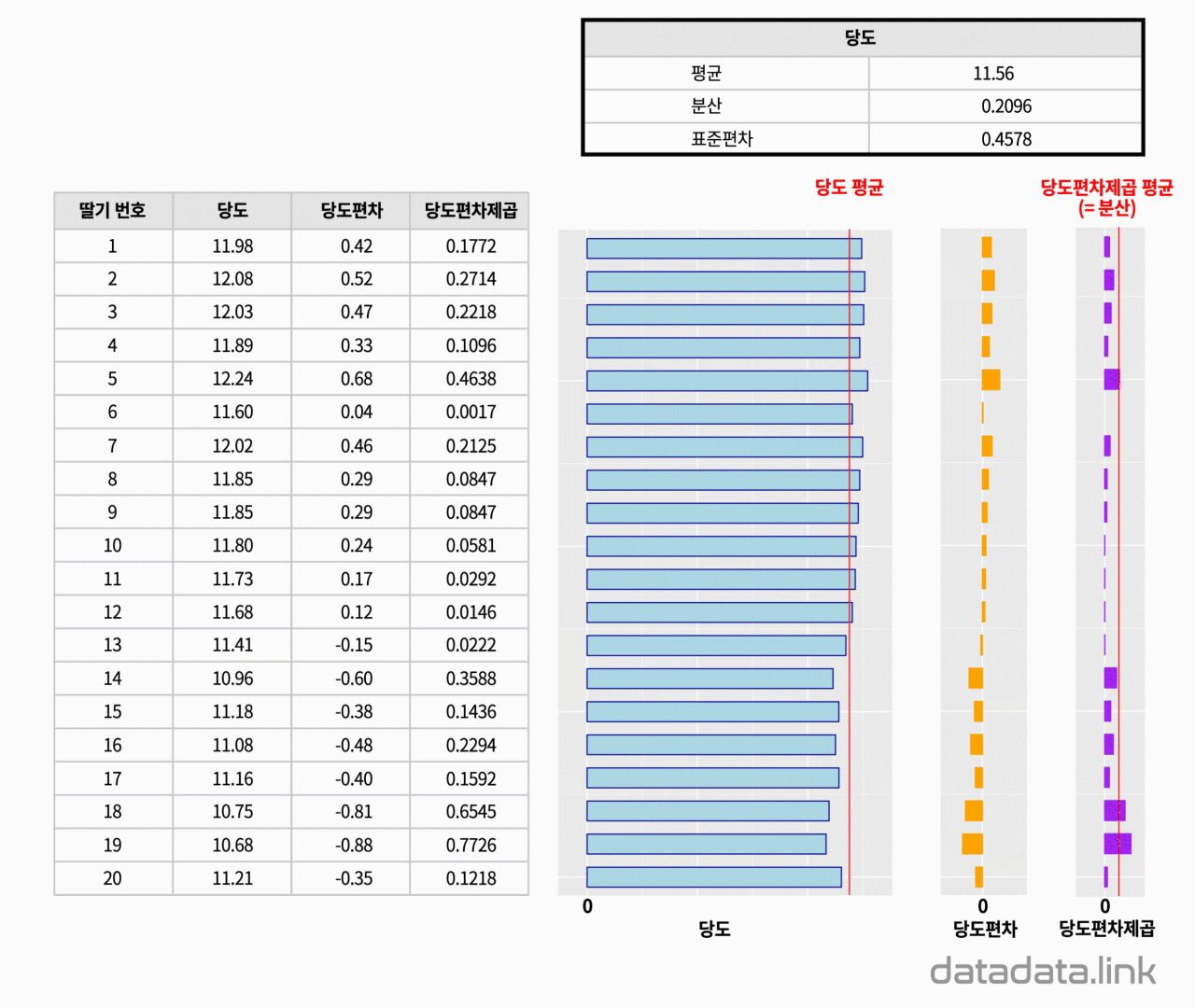
20개의 딸기의 당도 데이터가 있습니다.
즉, 20개의 숫자입니다.
20개의 숫자 무리를 대표하는 것에는 무엇이 있을까요.
일단 당도의 평균인 11.89라는 값이 있습니다. 20개의 당도를 대표하는 값입니다.
그리고 평균으로 부터 20개의 값들이 얼마나 떨어져 있는지도 궁금합니다.
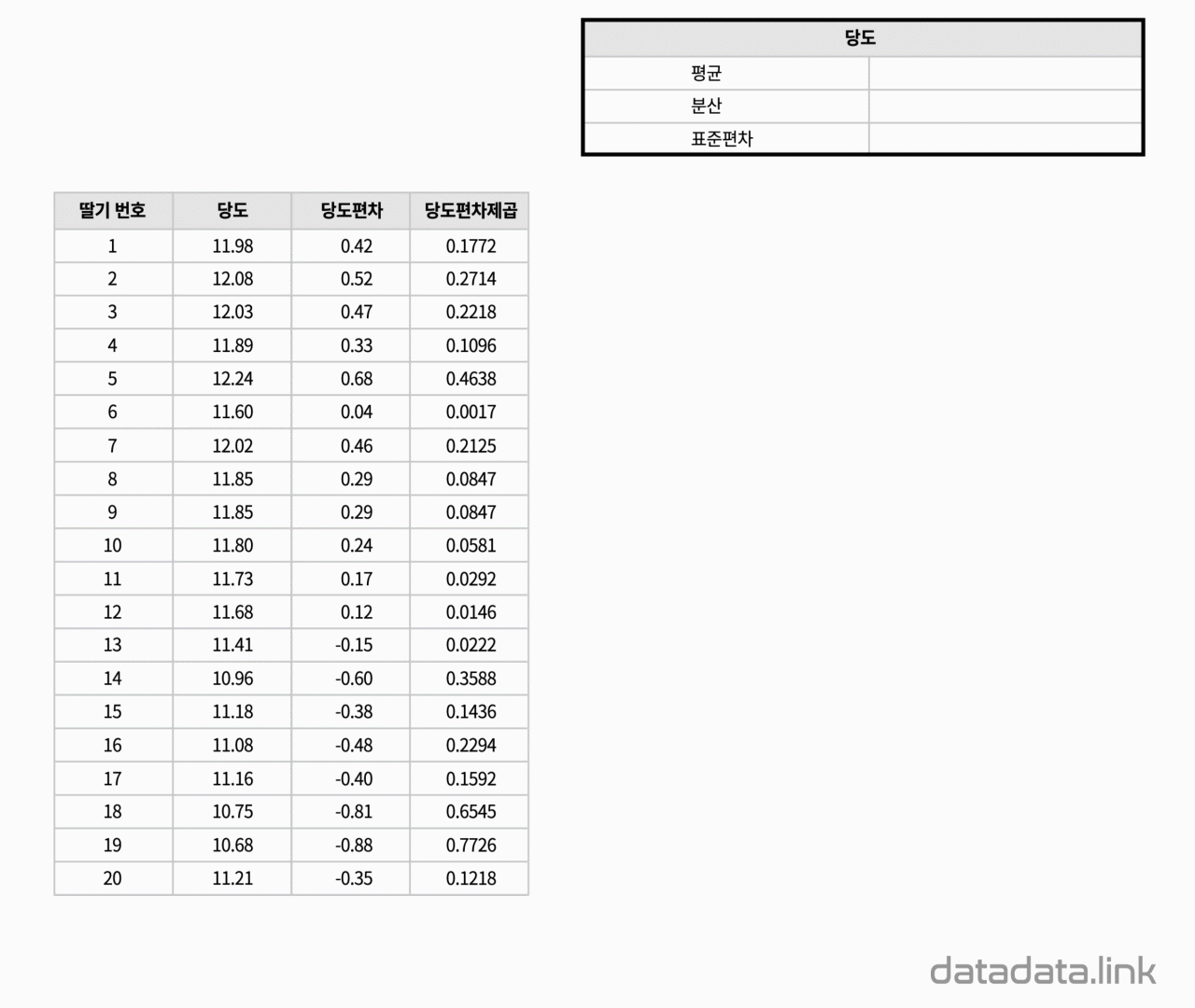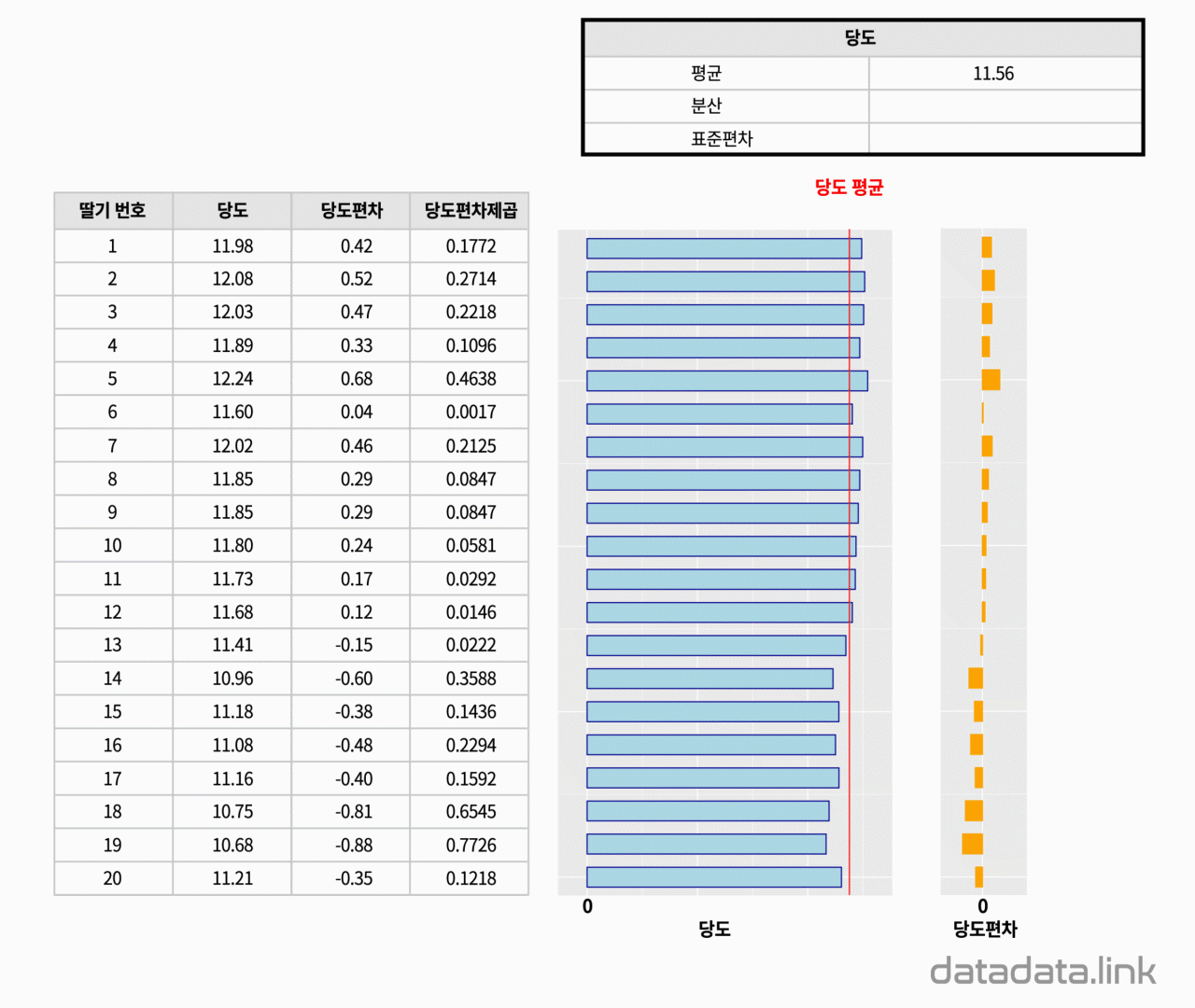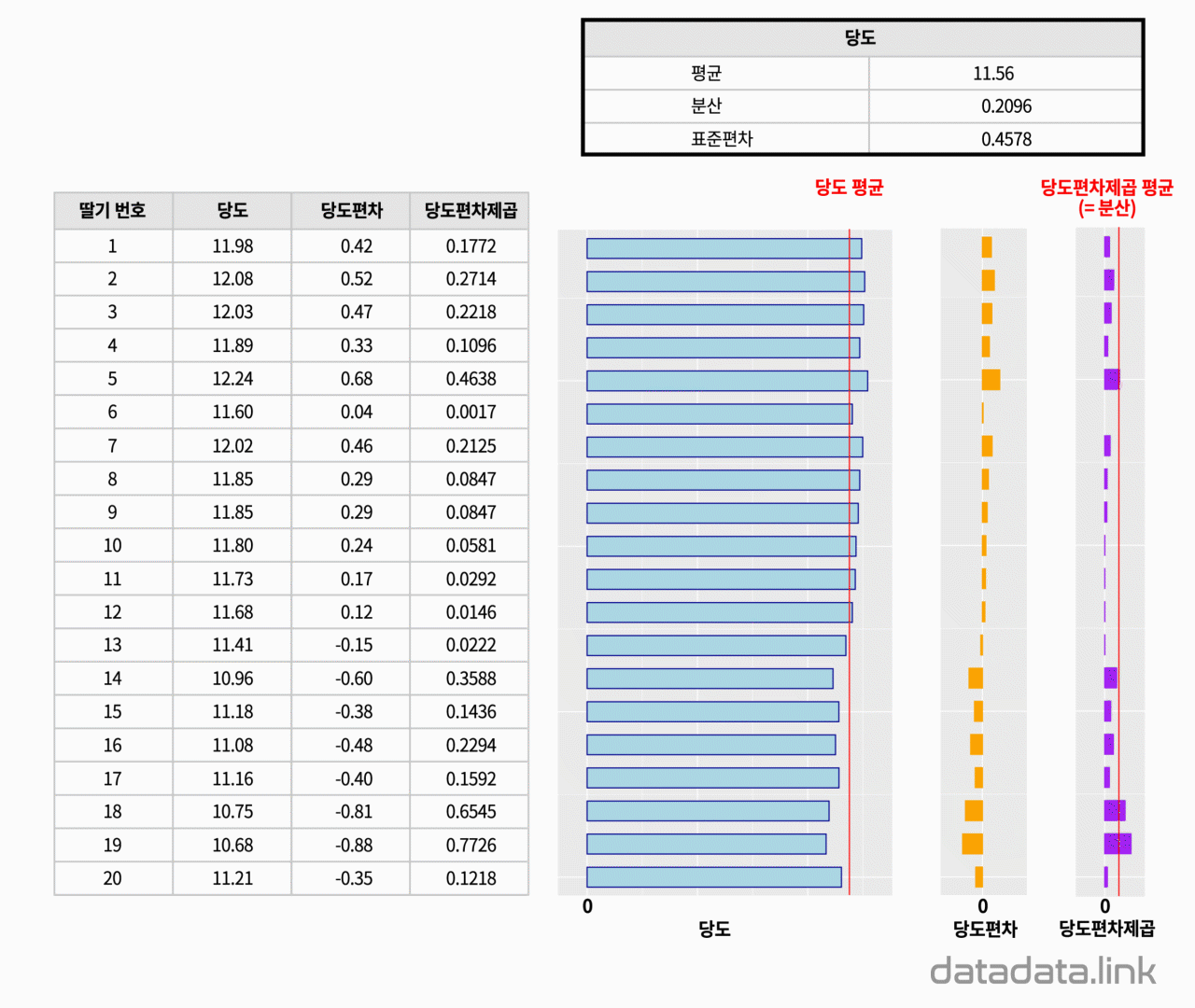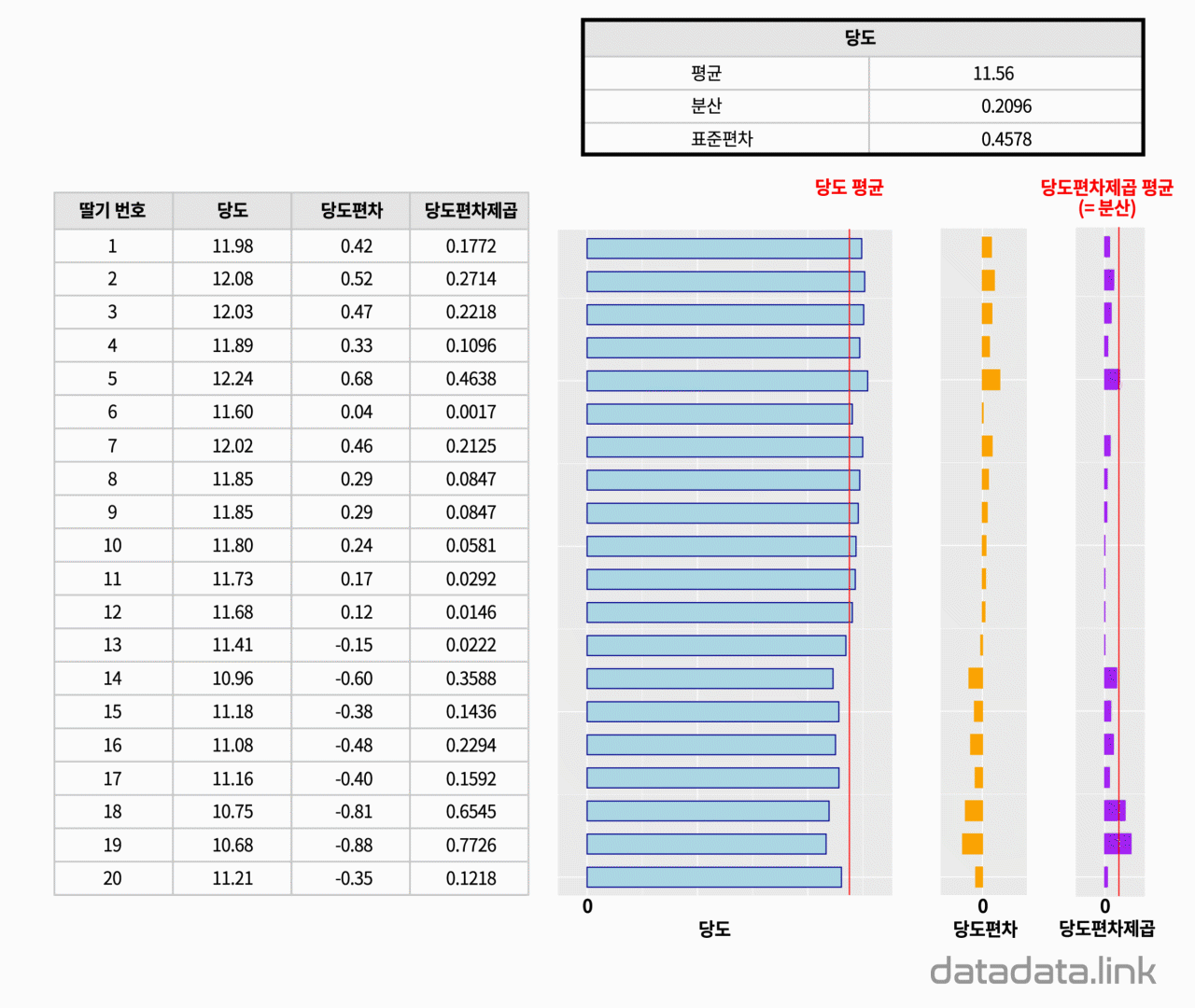
그것이 분산입니다. 여기서는 0.1245라는 값입니다. 분산의 값이 커지면 20개의 당도 값은 서로 많이 떨어져 있다는 뜻입니다.
그렇다면 분산은 어떻게 구할까요.
평균으로 부터 떨어진 거리를 편차라 할때 편차 제곱의 평균을 구한 것입니다.
즉, 평균으로 부터 떨어진 거리를 제곱한 값들을 숫자무리의 자유도로 나눕니다. 숫자무리가 모집단인 경우는 자유도가 숫자의 갯수이고 숫자무리가 표본인 경우는 자유도가 숫자의 갯수에서 1을 뺸 값입니다.
그리고 당도값과 같은 단위로 나타내기 위하여 분산을 다시 제곱근을 하여 구한 표준편차도 있습니다.
당도값 20개가 이루는 숫자무리를 표현함에 있어 다음 세가지로 정리해 보겠습니다.
첫째는 20개의 당도가 있고 그 당도들은 하나의 대표값으로 표현할 수 있습니다. 평균입니다.
둘째는 20개의 값이 평균으로 부터 떨어진 거리가 20개있고 그 거리들을 하나의 대표값으로 표현할 수 있습니다. 표준편차입니다.
세째는 숫자무리를 표현하는 통계량에는 평균, 분산, 표준편차가 있다는 것입니다.
3. 실습
3.3. 실습강의
데이터
평균
편차
편차제곱
분산
표준편차
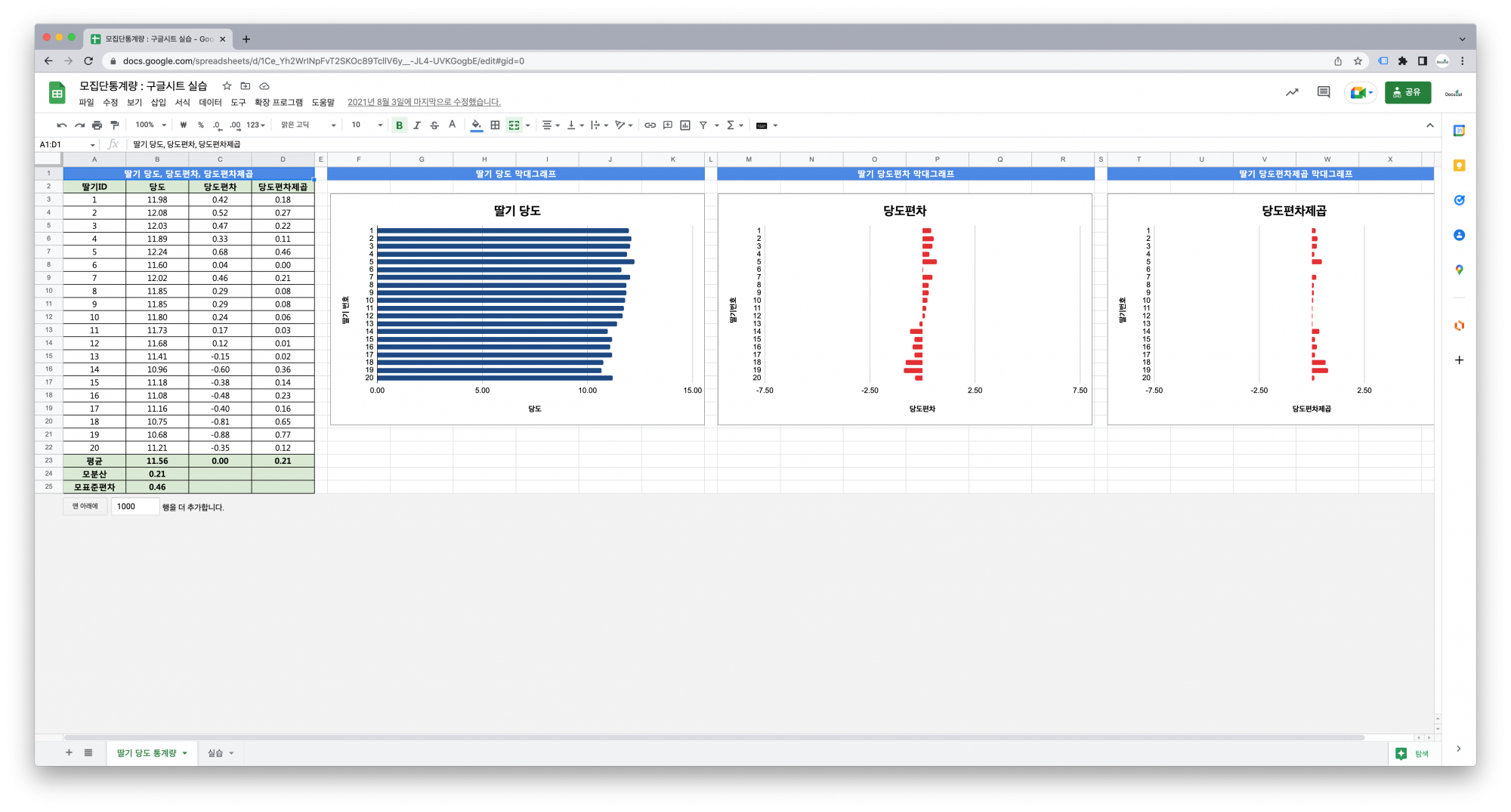
데이터시각화
4. 용어와 수식
4.1 수식