3차원 좌표계 ?
3D coordinate system ?
1.1. 3차원 직교좌표계
1. 애니메이션
2. 설명
2.1 3차원 직교좌표계
세 변수를 가지는 요소(element, 객체, object)를 시각화 할 때, 3차원(공간)좌표계를 많이 사용합니다. 3차원(공간)좌표계에는 대표적으로 차원(three dimensions) 직교좌표계(Cartesian coordinate system)가 있습니다. 여기서 세 좌표축(axis)은 직각을 이루어서 서로 영향을 주지 않습니다.
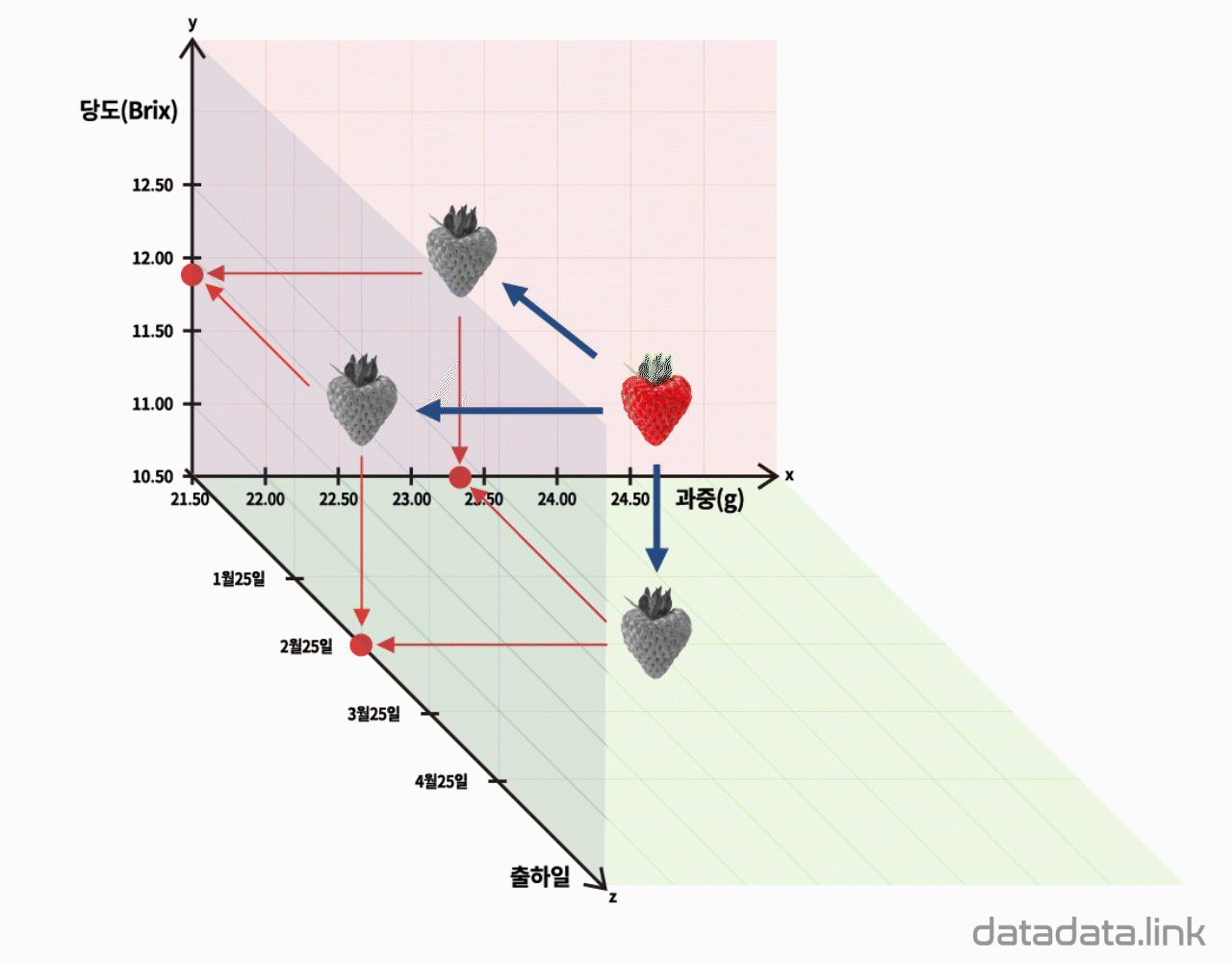
예를 들어 위의 애니메이션에서 보는 바와 같이 딸기를 요소라 하면 딸기의 당도와 과중과 출하일은 변수가 됩니다. 이때 딸기를 점(point)로 생각한다면 당도와 과중과 출하일을 세 축으로 하는 3차원 직교좌표계를 사용하여 산점도를 그릴 수 있습니다.
다른 관점으로 공간에서의 한 점(point)을 표현하는 방법에는 대표적으로 직교좌표계(Cartesian coordinate system)가 있습니다. 세개의 선이 직각(perpendicular)으로 교차하는 좌표축(coordinate axis)을 가집니다. 공간의 한 점은 기준(Origin)에서의 거리를 좌표로 합니다. 그리고 그 거리는 같은 단위를 가집니다. 따라서 공간의 한 점은 세개의 좌표값으로 표현할 수 있습니다. 즉, 공간의 한점은 세개의 좌표의 변수값을 가집니다.
공간좌표는 세개의 변수들의 관계를 나타내고 있기 때문에 3차원(three dimensions) 좌교계라고도 합니다. 한편, 평면좌표는 두개의 변수들의 관계를 나타내고 있기 때문에 2차원(two dimensions)좌표계라고 합니다.
2.2. 원통좌표계
한 개체에서의 속성으로 두 원인변수와 확률밀도, 세가지를 가질 때, 원통좌표계(cylindrical coordinate system)를 많이 사용합니다.
2.3. 복소3차원공간
복소3차원공간(complex 3D space)은 복소평면을 포함하는 3차원 좌표계입니다. 이 좌표계에서는 하나의 축이 실수부를, 다른 하나의 축이 허수부를 나타내며, 세 번째 축은 추가적인 차원(예를 들어, 물리적 공간의 한 차원 또는 다른 수학적 차원)을 나타내는 데 사용합니다.
3. 실습
3.2. 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
3.3. 실습강의
– 데이터
– 범위
– 산점도