2.1. 복제(複製)와 자연상수

은행A는 예금자와 합의한 기간 동안 예금액을 복제해주는(2배로 불려 주는) 은행입니다. 다르게 표현하면 예금액에 더해 예금액과 같은 금액의 이자를 주는 은행입니다. 

$$Y=I+I\dfrac{T}{T}=2I$$

여기서 $Y$는 출금액

$I$는 예금액

$T$는 합의한 기간

예를 들어, 예금자와 은행이 합의한 예치기간을 1년으로하고 에금액을 1억으로 하면 합의한 기간인 1년 후에 예금자는 예금액의 2배인 2억을 출금할 수 있습니다. 다르게 표현하면 예금액 1억과 불려진 금액(이자)인 1억의 합이 출금액 2억원이 됩니다.

$$Y=1+1\dfrac{1}{1}=2 \,\, \text{억원}$$

은행B는 은행A와 마찬가지로 합의된 기간 동안 예금액을 2배로 불려주는데, 은행A와 다른 점은 합의된 예치기간내라도 출금을 할 수 있고 출금시 원금과 예치기간에 비례한 이자를 주는 은행입니다.

$$Y=I+I\dfrac{t}{T}$$

여기서 $Y$는 출금액

$I$는 예금액

$T$는 합의한 기간

$t$는 예치한 기간 ; $t  ≤ T$

예를 들어, 예금자와 은행이 합의한 예치기간을 1년으로 하고 1억을 예금하고 반년 후에 출금하면 예금 1억과 이자 0.5억원을 받습니다. 이를 다시 남은 반년간 예치하면 입금 1.5억과 이자 0.75억원을 받습니다. 정리하면, 합의한 기간을 반으로 나누어 입금과 출금을 연속적으로 진행하면 합의한 기간인 1년 후에 2.25억원을 받습니다.

$$Y=\left(1+1\cdot\dfrac{1}{2}\right) +\left(1+1\cdot\dfrac{1}{2}\right)\dfrac{1}{2}=\left(1+1\cdot\dfrac{1}{2}\right)^2 \text{억원}$$

위식을 일반화하면

$$Y=\left(I+I\cdot\dfrac{1}{n}\right)^n$$

여기서,  $Y$는 합의기간 후의 출금액

$I$는 처음 입금액

$n$은 1기간(표준화된 합의기간) 동안 “입금하고 출금하기” 회수

위 두가지 결과로 추론하면 예금자는 은행B를 선택하고 입금과 출금을 많이 하면 할수록 합의된 기간이 지난 후 더 많은 금액을 받을 수 있습니다. 또한, 입금과 출금을 연속적으로 반복하면 합의된 기간 후의 출금액은 수렴하며 최대출금액이 됩니다. 이를 다음식과 같이 일반화할 수 있습니다.  첫 입금액($I$)가 1이고 합의한 기간을 1로하면 출금액은 수렴하는 데 이 수렴값을 자연상수(Euler’s number, natural constant, $e$)라고 합니다. 자연상수($e$)는 무리수이며 정수, 2와 반복하지 않는 무한소수,  $0.718\cdots$의 합입니다.

$$Y=\lim_{n \to \infty} (I+I\cdot\dfrac{1}{n})^n=I^n e$$

여기서 $Y$는 합의기간 후 출금액

$I$는 처음 입금액

$n$은 “입금하고 출금하기” 횟수

위의 결과를 종합하면 정해진 1단위금액을 합의된 1단위시간동안 복제하는(2배로 만들어 주는) 은행이 있다면 1단위시간동안 입출금을 무한번 반복하면 1단위시간 후의 출금액은 수렴하며 가능한 최대출금액이 됩니다.

2.2. 붕괴(崩壞, decay)와 자연상수

방사성물질 A는 일정기간이 지나면 붕괴하는(질량이 반으로 주는) 물질입니다.

$$Y=I-\dfrac{I}{2}\dfrac{T}{T}=\dfrac{1}{2}I$$

여기서 $Y$는 반감기가 지난 후의 질량

$I$는 처음 질량

$T$는 반감기

예를 들어, 방사성물질 A가 반감기가 1년이고 처음 질량을 1g으로 하면 1년 후에 질량은 $\dfrac{1}{2}\mathrm{g}$이 됩니다.

$$Y=1-\dfrac{1}{2} \times \dfrac{1}{1}=\dfrac{1}{2}\mathrm{g}$$

방사성물질A가 연속적으로 붕괴하도록 하는 환경이 조성된다면 방사성물질A의 질량은 다음식으로 표현할 수 있습니다.

$$Y=\left(I-I\cdot\dfrac{1}{n}\right)^n$$

여기서 $Y$는 반감기가 지난 후의 질량

$I$는 처음 질량

$n$은 1기간(반감기) 동안 붕괴회수

붕괴회수를 극대화하면 다음과 같습니다.

$$Y=\lim_{n \to \infty} (I-I\cdot\dfrac{1}{n})^n=I^n e^{-1}$$

여기서 $Y$는 남은 질량

$I$는 처음질량 : $I$가 1이면 $Y$는 $e$로 수렴

$n$은 붕괴회수

위의 결과를 종합하면 처음 질량이 일정기간 동안 반이 되는 방사성원소가 있다면 그 기간동안 붕괴를 연속적으로 진행하면 붕괴 후의 질량은 수렴합니다. 이 때의 수렴된 값의 역수를 자연상수라 합니다. 자연상수는 무리수이며 $2.718\cdots$입니다.

2.3. 재귀식(recursive formula)과 자연상수

팩토리얼(factorial)은 다음과 같이 정의됩니다.

$$n!=n\times(n-1)\times, \ldots , \times 1$$

여기서, $n$은 0과 자연수이며 $0!=1$ 이고 $1!=1$

팩토리얼을 재귀식(recursive formula)으로 표현하면 다음과 같습니다.

$$f(0)=1$$

$$f(n)=n \times f(n-1) \,\, \text{for} \,\, n \gt 0$$

자연상수를 재귀식으로 표현하면 다음과 같고 $n$이 증가하면 자연상수에 가까워집니다.

$$e(0)=1$$

$$e(n)=e(n-1) \times \dfrac{1}{f(n)} \,\, \text{for} \,\, n \gt 0$$

자연상수를 무한급수형태의 재귀함수로 표현하면 다음과 같습니다.

$$e=\sum\limits_{n=0}^{n=\infty}\dfrac{1}{n!}$$

2.3. 미분방정식과 자연상수

다음 미분방정식은 미분값이 값의 배수와 같음을 나타내는 방정식입니다. 즉, $x$에 대한 $y$의 변화율이 $y$자신에 비례하는 모델입니다. 이러한 유형의 방정식은 자연 세계에서 많이 발견되며, 예를 들어 방사성붕괴나 인구성장 모델이 있습니다.

$$\dfrac{dy}{dx}=ky$$

여기서, $y$는 종속변수

$x$는 독립변수

$k$는 상수

이 미분방정식을 만족시키는 함수는 다음과 같습니다

$$y=Ce^{kx}$$

여기서, $e$는 자연상수

$C$는 초기 조건에 따라 결정되는 상수

$k$는 상수

자연상수는 이러한 유형의 미분방정식을 만족하는 지수함수에서 나타나며, 지수적 성장이나 감소를 모델링하는 데 중요한 역할을 합니다.

2.4. 지수함수와 자연상수

자신을 $x$번 곱해도 자신이 되는 수를 1로 정의하며 지수함수의 밑의 기준이 됩니다. 

$$1^x = 1$$

모든 실수는 자신을 0번 곱하는 것을 1로 정의하며 0은 지수함수의 지수의 기준이 됩니다.

$$a^0 \equiv 1$$

지수함수는 다음과 같이 표현합니다.

$$y=f(x)=a^x$$

여기서, $a$는 양의 실수

$x$가 0일 때의 $x$에 대한 $y$의 변화율(기울기)을 표현하면

$$f^{\prime}(0)=\lim\limits_{\Delta x \to 0}\dfrac{a^{0+\Delta x}-a^0}{\Delta x}=\lim\limits_{\Delta x \to 0}\dfrac{a^0(a^{\Delta x}-1)}{\Delta x}=a^0\left(\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}\right)=\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}$$

여기서,  $\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}$는 수렴

$a=2$이면 $\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}=0.6931472\cdots$

$a=3$이면 $\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}=1.0986123\cdots$

$f^{\prime}(0)=a^0\cdot \ln a=1$일 때의 $a$를 구하면 $a$는 $2.718\cdots$인 무리수이며 이를 자연상수 $e$라고 합니다.

$$\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}=1$$

여기서,  $a$는 $2.718\cdots$인 무리수이며 자연상수

지수함수의 미분함수(도함수)를 일반화하면

$$f^{\prime}(x)=\lim\limits_{\Delta x \to 0}\dfrac{a^{x+\Delta x}-a^x}{\Delta x}=\lim\limits_{\Delta x \to 0}\dfrac{a^x(a^{\Delta x}-1)}{\Delta x}=f(x)\left(\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}\right)=f(x)g(a)$$

여기서, $a^{x+\Delta x}=a^{x} a^{\Delta x}$

$0 < a$

$g(a)$는 $\lim\limits_{\Delta x \to 0}\dfrac{a^{\Delta x}-1}{\Delta x}$이며 $a$에 따라 다른 값으로 수렴하는 함수

2.5. 자연상수 (Natural constant, $e$) 성질

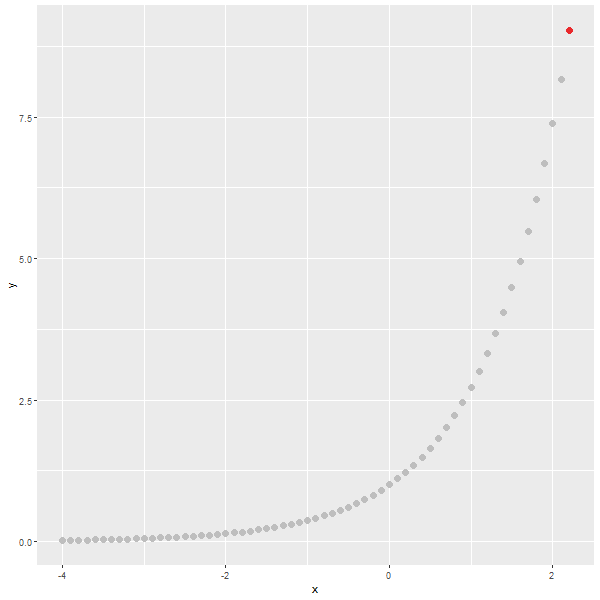
자신을 $x$번 곱해서 나오는 값이 $x$에서의 기울기인 수가 자연상수 $e$입니다. 자연상수($e=2.718\cdots$)는 무리수입니다. $e$를 $x$번 곱해서 나오는 값인  $e^x$을 두 변수, $x$와 $y$가 이루는 직교좌표계에서 함수로 표현하면

$$y=f(x)=e^x$$

원함수를 미분하여 표현하면

$$\dfrac{dy}{dx}=f^{\prime}(x) =\dfrac{d(e^x)}{dx} = e^x$$

원함수를 적분하여 표현하면

$$\int ydx=F(x)=\int_{-\infty}^{x}e^tdt= e^x$$

여기서,  $\lim\limits_{x \to -\infty} e^x=0$

원함수와 미분함수와 적분함수가 모두 같습니다. 모두 자연상수가 밑이 되는 지수함수입니다. 자연상수를 밑으로 하는 지수함수, 즉, 자연 지수함수는 정의역에 따라 다음과 같이 표현할 수 있습니다.

$$f(x)=e^x$$

여기서,  $x < 0$ 이면  $f(x)=\left(\dfrac{1}{e}\right)^{ㅣxㅣ}$

$x = 0 $ 이면  $f(x)= 1$

$x > 0$ 이면  $f(x)=e^x$

단위기간을 나눈 무한횟수($n$)로 표현하면

$$e=\lim_{n \to \infty} \left(1+{\dfrac {1}{n}}\right)^{n}$$

단위기간의 나누어진 극소시간($t$)로 표현하면

$$e=\lim_{t \to 0} \left(1+t\right)^{\frac{1}{t}}=e$$

자연상수를 급수(series)로 표현하면

$$\eqalign{e=\sum_{n=0}^{\infty}\dfrac{1}{n!} &= \dfrac{1}{0!} + \dfrac{1}{1!} + \dfrac{1}{2!} + \dfrac{1}{3!} + \cdots \cr&= \dfrac{1}{1} + \dfrac{1}{1} + \dfrac{1}{1\cdot 2} + \dfrac{1}{1\cdot 2\cdot 3} + \cdots}$$

자연로그와의 관계는 

$${\rm ln}\left(e^x\right) = x \,\, , \,\, e^{{\rm ln} (x)} = x$$

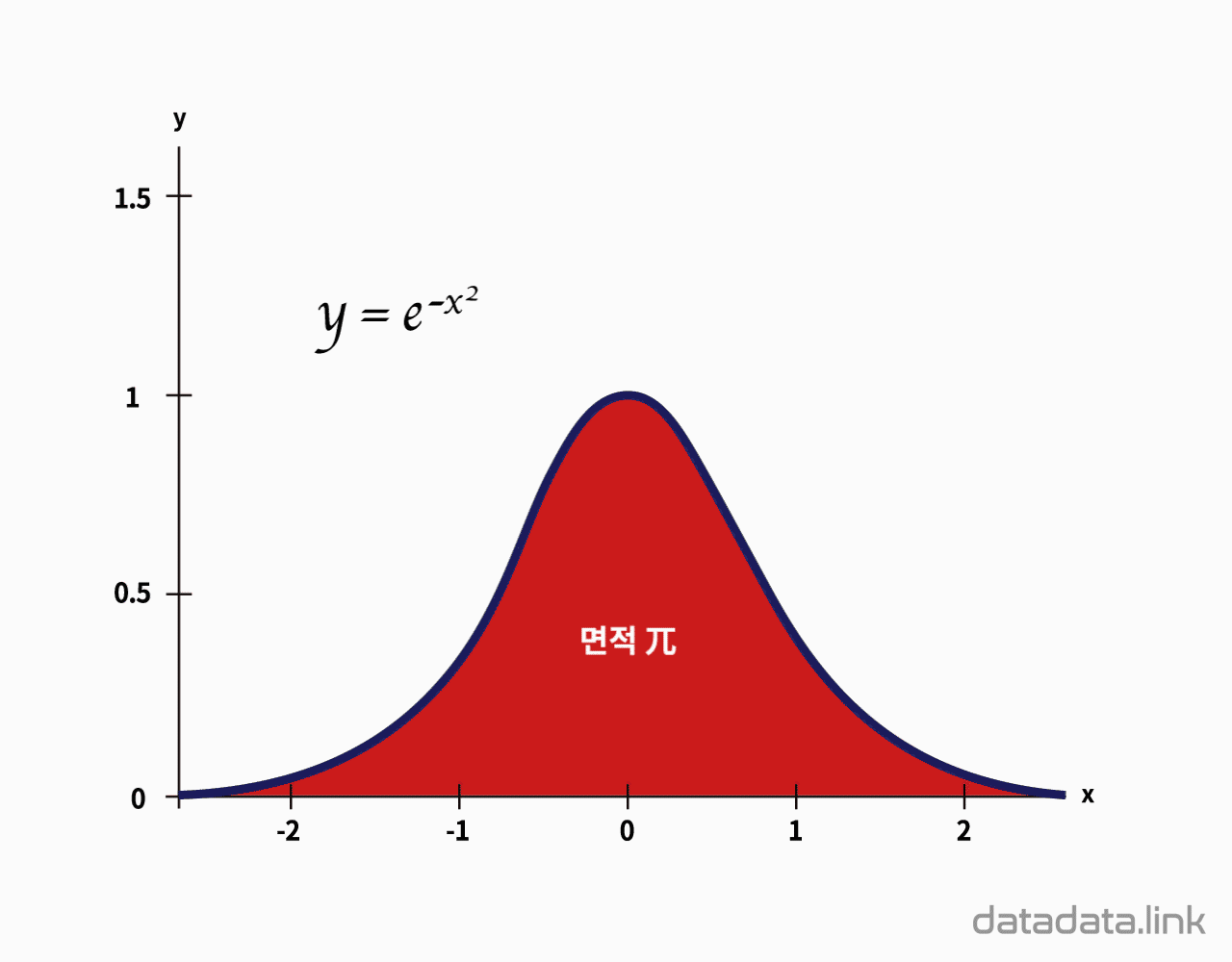
가우스 적분

$$\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}$$

임의의 가우스적분(arbitrary Gaussian function)

$$\int _{-\infty }^{\infty }e^{-a(x+b)^{2}}\,dx=\sqrt {\dfrac {\pi }{a}}$$

베르누이 시행

$$\binom {n}{k}\left({\dfrac {1}{n}}\right)^{k}\left(1-{\dfrac {1}{n}}\right)^{n-k}$$

베르누이 시행에서 $k$가 0이고 $n$이 무한대이면

$$\lim\limits_{n \to \infty} \left(1-{\dfrac {1}{n}}\right)^{n}=\dfrac{1}{e}$$

로그함수 미분

$$\dfrac {d}{dt}\log _{e}t=\dfrac {1}{t}$$

로그함수 적분

$$\int _{1}^{e}{\dfrac {1}{t}}\,dt=1$$

자연 지수함수의 생성상수가 $\tau$일 때

$$\tau =\dfrac{f(t)}{f'(t)}$$

$$f(t+\tau )=ef(t)$$

2.6. 자연상수 시각화

극좌표계

극좌표계에서 원점에서의 거리, $r$이 시간($t$)에 따라 지수함수적으로 작아지고 각속도($\dot{\theta}$)가 상수인 $2\pi$로 등속일 때 2차원 평면에서 점의 움직임을 수식으로 표현하면 다음과 같습니다.

$$\dfrac{dr}{dt}= \left(\dfrac{1}{e}\right)^t$$

여기서, 시간($t$)는 0에서 시작하여 커지는 실수

점의 각속도

$$\dfrac{d\theta}{dt}=2\pi$$

여기서, 시간($t$)는 0에서 시작하여 커지는 실수. 그리고 $\theta$는 직각좌표계의 $x$축 방향에서 시작

직각좌표계

점의 $x$축에서의 출현 횟수는 단위시간 1당 1번

$$\dfrac{dl}{dt}=2{\pi}e^t$$

여기서,  $\dfrac{dl}{dt}=2{\pi}\dfrac{dr}{dt}$

모든 각도에서 점이 무한대로 있고 운동하면

2.7. 자연상수 적용

복리 적금

복리 적금의 원금과 이자의 합계(원리 합계)는 다음의 식과 같이 계산할 수 있습니다.

 

원리합계 = 원금 × (1 + 이자율)^기간

 

원리합계는 원금과 이자율과 기간이 결정한다는 것을 알 수 있습니다. 기간이 무한하게 커져도 원리합계가 수렴하는 경우는 이자율과 기간이 서로 반 비례하는 경우입니다. 

미분방정식으로 표현하면

$$\dfrac{dM}{dt}=(1+r)M$$

여기서,  $M$은 $t$의 함수이며 $M(t)$는 $t$시간이 흐른 후 찾을 수 있는 금액

$r$은 이자율

미분방정식을 풀면

$$M(t)=e^{(1+r)t}$$

여기서,  $M$은 $t$의 함수이며 $M(t)$는 $t$시간이 흐른 후 찾을 수 있는 금액

$r$은 이자율

자기복제

우선, 이산적(discrete)인 경우의 자기복제를 생각해 봅니다. 초기량를 1이라 하고 단위 복제 기간을 1이라고 한다면 1기간 후에는 자신의 초기량의 2배인 2가 됩니다.  복제가 연속적(continuous)으로 진행되는 경우는 복제가 진행되는 기간을 1 이라고 한다면 1기간 후에는 다음식과 같이 총량이 만들어 집니다.  총량은 초기량과 복제된 량의 합입니다.

 

$$\mathop{\lim}\limits_{{t}\rightarrow{o}}{\left({{1}{+}{t}}\right)}^{\frac{1}{t}}{=}\mathop{\lim}\limits_{{n}\rightarrow\infty}{\left({{1}{+}\frac{1}{n}}\right)}^{n}$$

 

이 값의 최대값은 단위 1기간을 무한개의 기간으로 나누면  $e$로 수렴합니다.

 

$$\mathop{\lim}\limits_{{t}\rightarrow{o}}{\left({{1}{+}{t}}\right)}^{\frac{1}{t}}{=}\mathop{\lim}\limits_{{n}\rightarrow\infty}{\left({{1}{+}\frac{1}{n}}\right)}^{n}=e$$

 

정리하면, 크기 1이 1기간 동안 생성률(미분계수) 1로 시작하여  무한 자기복제를 하면 수렴하게 되는데  그 값이 자연상수($e$)입니다. 자연상수($e$)는 무리수 입니다. 

 

$e = 2.71828…$

 

$${e}{=}\mathop{\lim}\limits_{{t}\rightarrow{o}}{\left({{1}{+}{t}}\right)}^{\frac{1}{t}}{=}\mathop{\lim}\limits_{{n}\rightarrow\infty}{\left({{1}{+}\frac{1}{n}}\right)}^{n}$$

온도평형

방안의 온도와 방안에 있는 찻잔 속의 뜨거운 물의 온도차이를 $\Delta T$라 하면 온도차이의 시간이 지남에 따라 줄어드는 속도는 온도차이에 비례합니다.

$$\dfrac{d\Delta T}{dt}=-k\Delta T$$

여기서,  $\Delta T$는 방안의 온도와 뜨거운 물의 온도차

자연에서 온도차($\Delta T$)는 다음식과 같이 관찰됩니다.

$$f^{\prime}(t)= -k f(t)$$

여기서, $f(t)=\Delta T$

$t$는 시간

$k$는 주어지는 상수

위의 함수  $f(t)$를 지수함수($a^t$)로 모델링할 수 있습니다.

$$f^{\prime}(t)=\lim\limits_{\Delta t \to 0}\dfrac{a^{t+\Delta t}-a^t}{\Delta t}=\lim\limits_{\Delta t \to 0}\dfrac{a^x(a^{\Delta t}-1)}{\Delta t}=f(t)\left(\lim\limits_{\Delta t \to 0}\dfrac{a^{\Delta t}-1}{\Delta t}\right)=-kf(t)$$

여기서,  $0<a≤1$

$k=-\lim\limits_{\Delta t \to 0}\dfrac{a^{\Delta t}-1}{\Delta t}$이며 $a$에 대한 함수

 $a$를 $e^{\ln a}$로 대치하면

$$f(t)=\Delta T(t)=e^{-kt}$$

3.2. 구글시트 함수

=EXP(1) : 자연상수 e의 거듭제곱. 괄호안의 숫자는 거듭제곱할 지수. 

=FACT(A3) : 계승. A3에 있는 값보다 작거나 같은 모든 양의 정수의 곱. 예를 들어, A3가 3이라면, 3의 계승은 3, 2, 1의 곱, 즉, $(3\times 2\times 1)$이 됨.

=2^2 : 거듭제곱. 2를 2번 곱함.

=LN(2) : 자연로그. 자연상수 e를 밑으로 하는 자연로그 값. e를 몇 제곱해야 2가 되는지 계산함. 따라서, =LN(EXP(1))의 값은 1이 됨.

4.1 용어

e (자연상수, mathematical constant)

오일러 수(Euler’s number)라고도 하는 상수 $e$는 대략 2.71828과 같은 수학적 상수로 여러 측면에서 규정될 수 있습니다. 자연로그의 밑입니다. $n$이 무한대에 가까워질 때의  $(1 + \dfrac{1}{n})^n$의 극한값입니다. 복리계산에서 보이는 표현입니다. 무한급수의 합으로 계산할 수도 있습니다.

 

또한 $e$는 함수 $y = ax$의 그래프가 $x = 0$에서 기울기가 1이 되도록 하는 고유한 양의 상수입니다. (자연)지수 함수 $f(x) = e^x$는 고유한 함수 $f$가 도함수와 동일하고 방정식 $f(0) = 1$을 충족합니다. 따라서 $e$를 $f(1)$로 정의할 수도 있습니다. 자연로그 또는 밑이 e인 로그는 자연 지수 함수의 역함수입니다. 숫자$k > 1$의 자연로그는 $x = 1$과 $x = k$사이의 곡선 $y = \dfrac{1}{x}$ 아래의 면적으로 직접 정의할 수 있습니다. 이 경우 $e$는 이 면적이 1일 때의  $k$의 값입니다.

 

상수 $e$는 수학자 Leonhard Euler의 이름을 따서 Euler’s number 또는 John Napier의 이름에서 Napier의 상수라고 합니다. 이 상수는 복리를 연구하던 중 스위스 수학자 Jacob Bernoulli가 발견했습니다. 상수 $e$는 $0$, $1$, $\pi$ 및 $i$와 함께 수학에서 매우 중요한 수입니다. 숫자 5개 모두 오일러의 항등식 $e^{i\pi }+1=0$에 나타나며 수학 전반에 걸쳐 사용됩니다. 상수 ${\pi}$와 마찬가지로 $e$는 무리수(정수 비율로 나타낼 수 없음)이고 초월적(유리계수가 있는 0이 아닌 다항식의 근이 아님)수입니다. 소수점 이하 50자리까지 $e$의 값은 다음과 같습니다.

2.71828182845904523536028747135266249775724709369995…

 

Reference

e (mathematical constant)

Product Integral

	additive	multiplicative
discreate	$$\sum_{i=a}^{b}f(i)$$	$$\prod_{i=a}^{b}f(i)$$
continuous	$$\int_{a}^{b}f(x)dx$$	$$\prod_{a}^{b}f(x)^{dx}$$

곱의 적분(product integral)은 미적분학의 일반적인 합의 적분과 상대되는 적분입니다. 곱의  적분은 1887년 수학자 Vito Volterra가 선형 미분 방정식 시스템을 풀기 위해 개발했습니다. 곱의 적분은 유행병학, 통계역학, 양자역학에 이르는 영역에서 사용됩니다. Geometirc 적분은  Geometric 도함수와 함께 이미지 분석 및 성장(growth)/쇠퇴(decay) 현상(예: 경제 성장, 박테리아 성장 및 방사성 붕괴) 연구에 유용합니다.Bigeometric 적분은 Bigeometric  도함수와 함께 프랙탈의 일부 응용과 경제학의 탄력성 이론에서 사용합니다.

 

Reference

Product integral – Wikpedia

Gausian Integral

오일러-푸아송 적분으로도 알려진 가우시안 적분은 가우시안 함수인 $f(x)=e^{-x^{2}}$의 실수에서의 적분입니다. 이 적분은 독일 수학자 칼 프리드리히 가우스의 이름을 따서 명명되었습니다.

$$\int _{-\infty }^{\infty }e^{-x^{2}}\,dx=\sqrt {\pi}$$

Abraham de Moivre는 1733년에 이러한 유형의 적분을 발견했으며, Gauss는 1809년에 이 적분을 발표했습니다. 이 적분에는 광범위한 응용 분야가 있습니다. 예를 들어, 약간의 변수 변경으로 정규 분포의 정규화 상수를 계산하는 데 사용됩니다. 정적분은 정규분포와 누적분포함수의 오류함수와 밀접한 관련이 있습니다. 예를 들어, 물리학에서 이러한 적분은 양자역학에서 조화 발진기의 기저 상태의 확률 밀도를 표현할 때 나타납니다. 이 적분은 또한 경로 적분 공식에서 고조파 발진기의 전파자를 찾기 위해, 그리고 통계역학에서 분할함수를 찾을 때 사용됩니다. 임의의 가우스 함수의 정적분은 다음과 같습니다.

$$\int _{-\infty }^{\infty }e^{-a(x+b)^{2}}\,dx=\sqrt {\dfrac {\pi }{a}}$$

Reference

Gaussian integral – Wikipedia

4.2. 참조

https://www.youtube.com/watch?v=m2MIpDrF7Es

로그함수 나무위키