2.1. 동전던지기와 큰수의 법칙

동전을 바닥에 던지면 앞면이나 뒷면 두면 중 하나만이 위를 향하게 됩니다. 즉, 동전 던지기의 결과는 앞면과 뒷면이라고 할 수 있습니다. 동전던지기를 시행이라고 하고 동전던지기 한번의 결과를 표본이라고 한다면 앞면과 뒷면은 표본이 나타나는 표본공간이라고 할 수 있습니다.

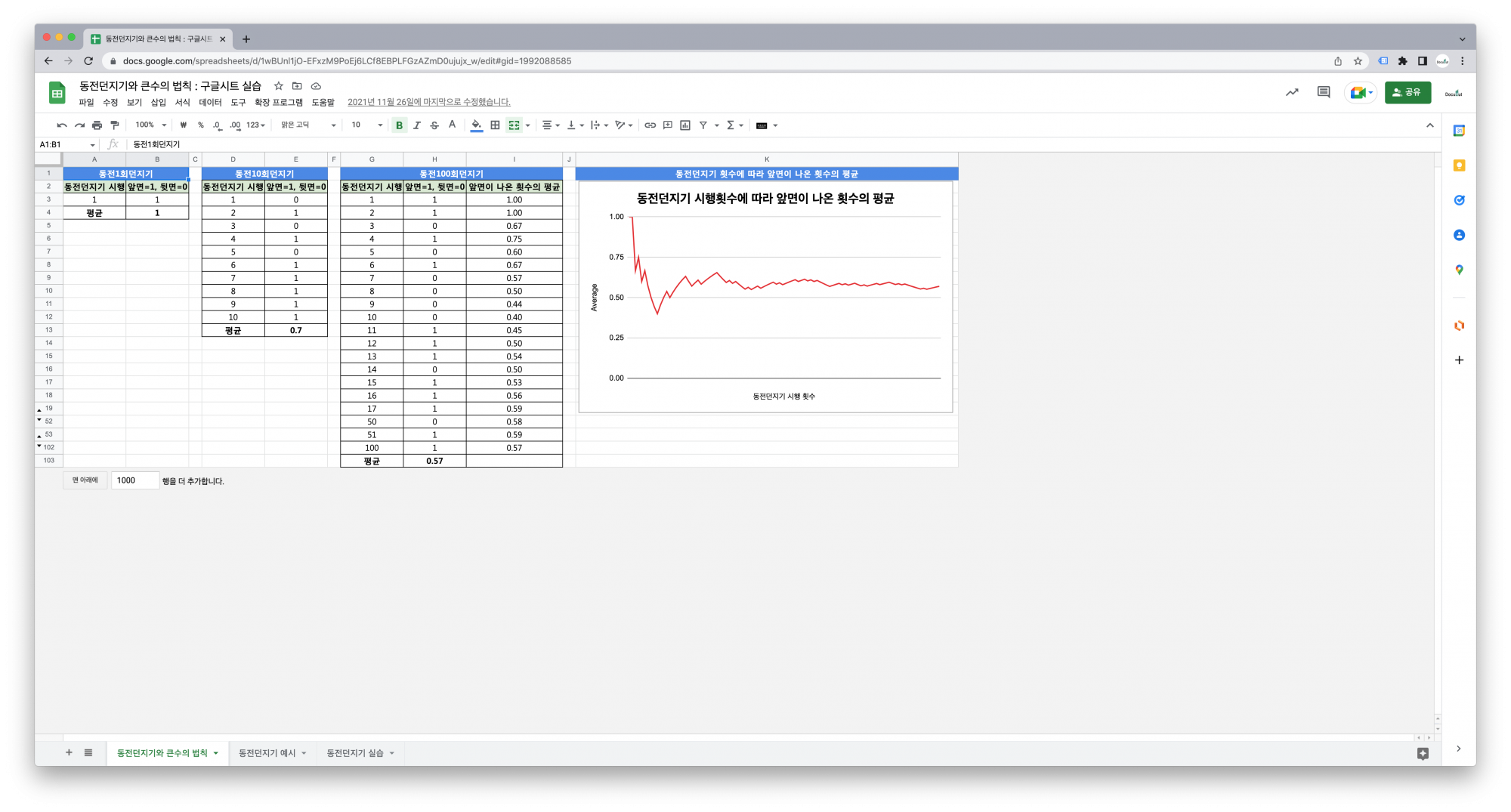
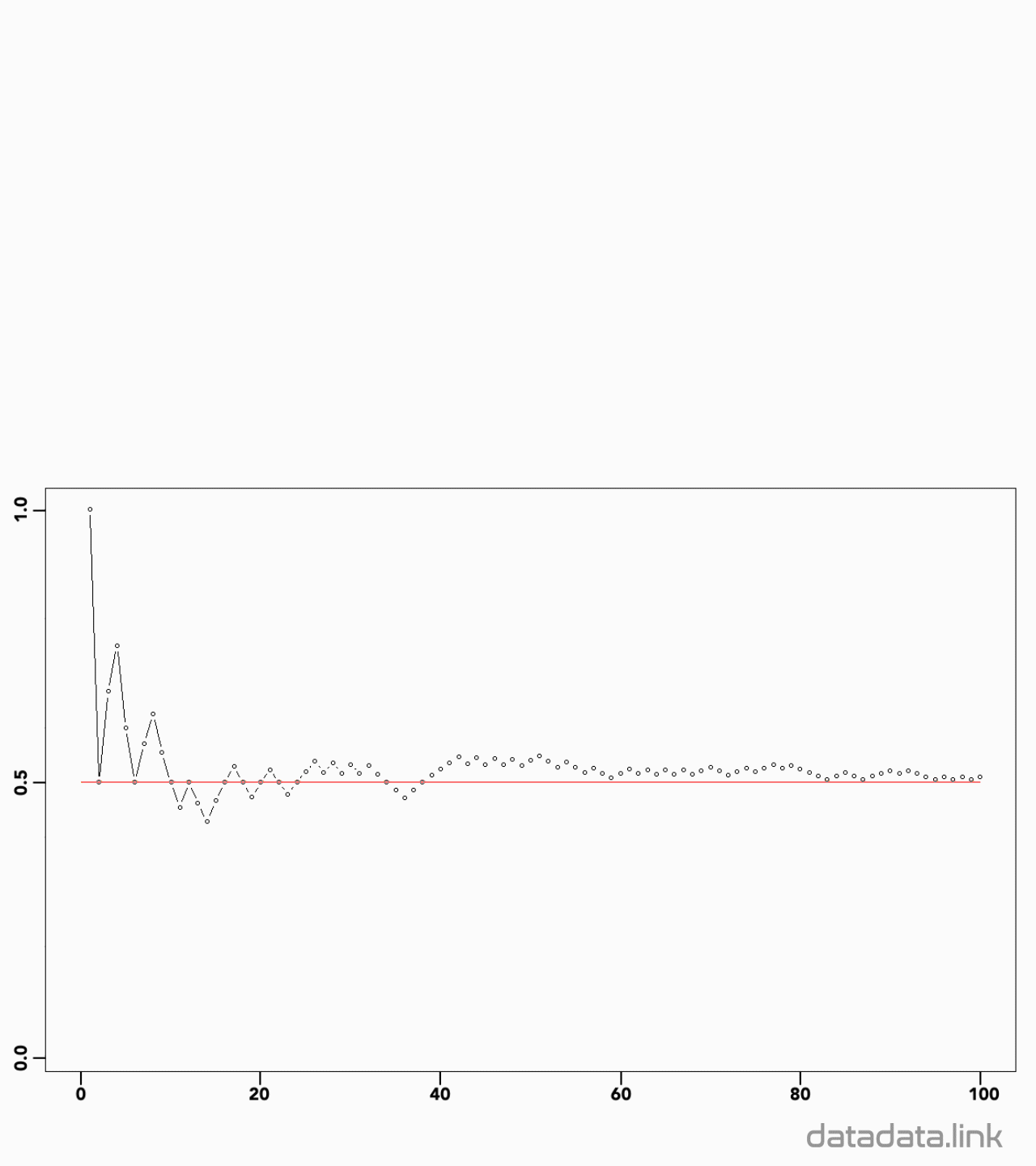
동전을 많이 던져서 큰 수의 표본을 준비하고 그 결과를 보겠습니다. 동전의 두 면에 0과 1이 표시된 동전을 준비합니다. 그리고 동전을 100회 던집니다. 그리고 100회 던질 때 마다 이제까지 시행된 결과의 합의 평균을 구합니다.

계속 던질 수록 시행된 결과의 합의 평균은 0.5에 점점 가까워짐을 알 수 있습니다. 이를 수렴(convergence)한다고 합니다. 시행을 많이 해서 시행의 결과(표집분포)의 대표값이나 분포값이 특정값에 수렴하는 것을 큰 수의 법칙이라고 합니다. 큰 수의 법칙은 확률과 통계를 이어주는 개념인 통계적 확률을 잘 설명해줍니다.

만일 0.5로 가까워져 가지 않고 0.6에 가까워 진다면 동전이 완벽하게 대칭이 아니고 찌그러진 동전이라고 할 수 있습니다. 즉,  한 동전을 무한대로 던지면 동전의 모양을 유추할 수 있게 됩니다. 이런 결과를 통계적 확률이라고 부릅니다.

3.2. 구글시트 함수

=준비 중 입니다. 

4.1 용어