갈톤보드와 큰 수의 법칙 ?
The law of large numbers from Galton board ?
2.1. 갈톤보드와 큰 수의 법칙
4.1. 용어
1. 애니메이션
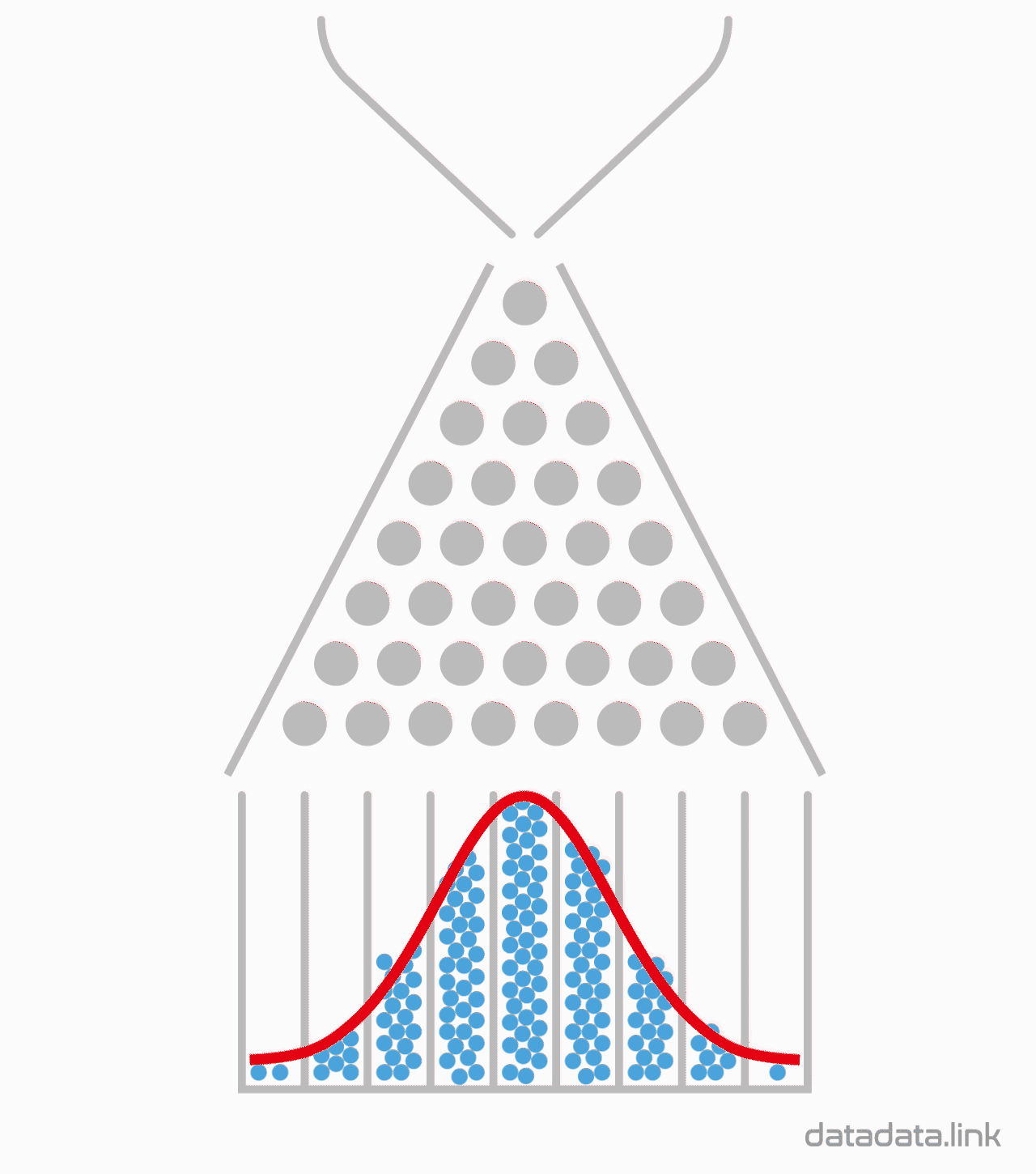

8개의 분기수를 가지는 Galton보드

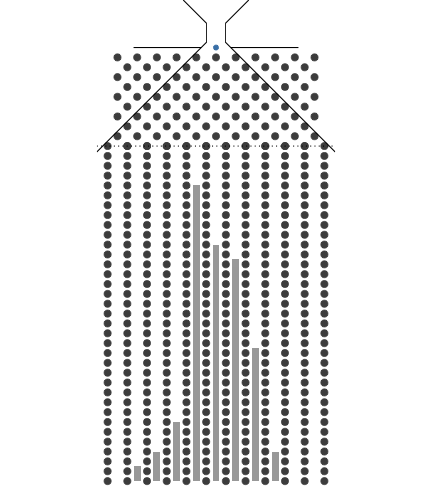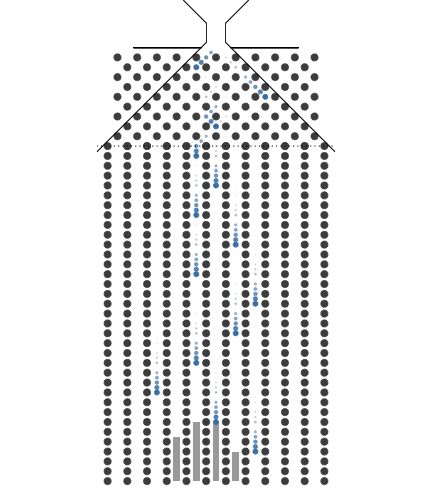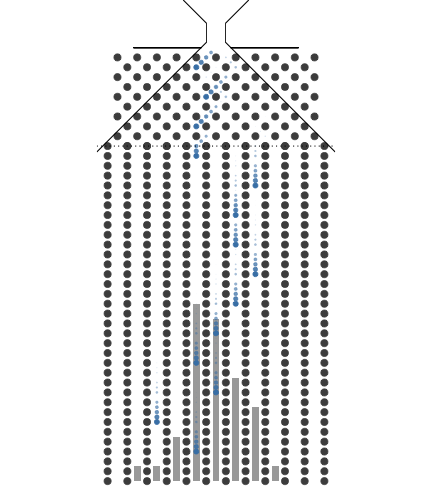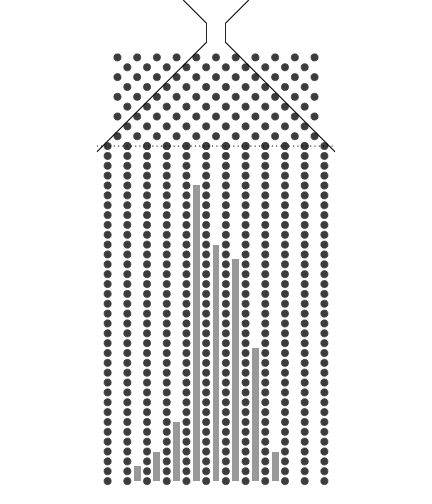
10개의 분기수를 가지는 Galton보드
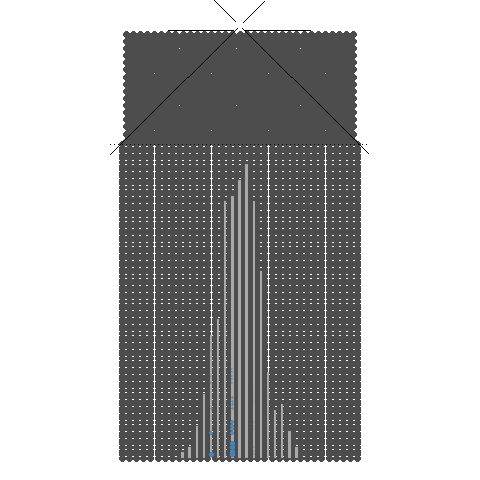
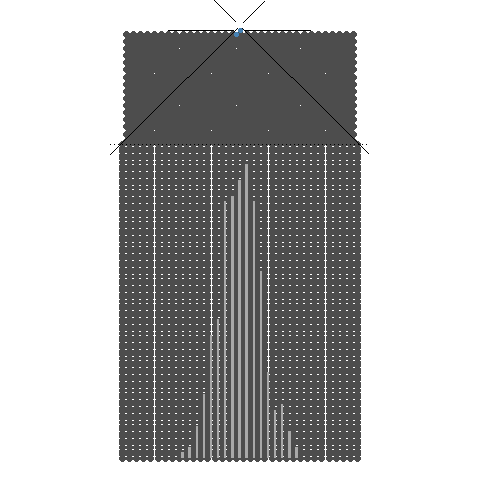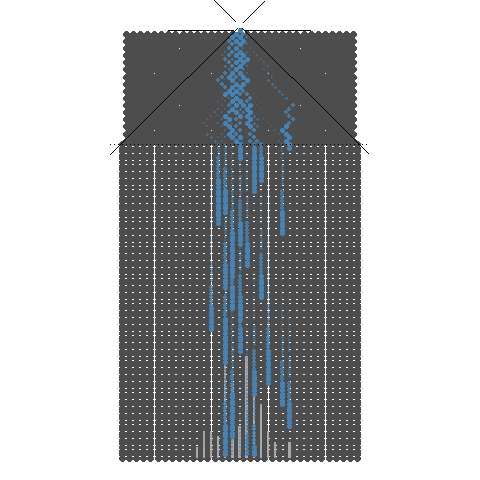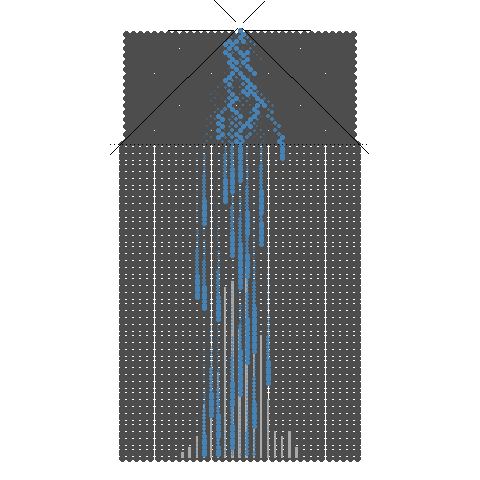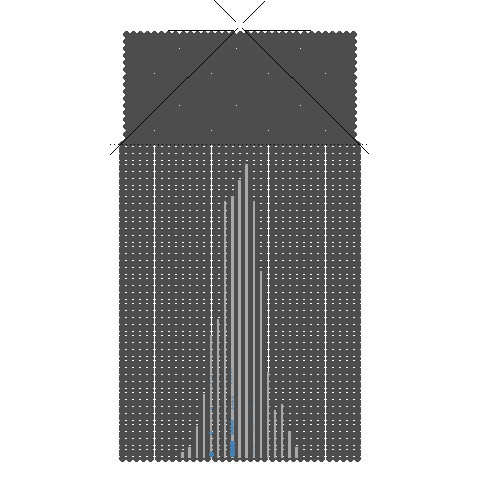
32개의 분기수를 가지는 Galton보드
2. 설명
2.1 갈톤보드와 큰 수의 법칙
갈톤보드(Galton board)의 특징을 살펴보겠습니다. 구슬 하나를 갈톤보드에 굴리면 구슬은 분기점을 만날때 마다 왼쪽이나 오른쪽으로 반드시 가게 됩니다. 다른 경우는 없습니다. 갈톤보드에서 구슬이 분기점을 만나는 횟수를 분기수라고 합니다. 갈톤보드의 분기수가 8개이면 9개의 칸이 생기고 10개면 11개, 32개면 33개의 칸이 생깁니다. 즉 분기의 갯수보다 분기에 의해서 만들어지는 아래 칸의 갯수가 하나 더 크게 됩니다.
예를 들어 8개의 분기수를 가진 갈톤보드를 보면 구슬이 내려가면서 8번의갈림길을 만나서 그 때마다 좌우의 길 중에서 하나의 길을 선택합니다.그리고 좌우로 가는 확률이 똑 같이 반반이라고 한다면 9개의 칸 중 5번째 칸에 구슬이 제일 많이 들어가는 종모양을 하게 됩니다. 구슬을 많이 굴리면 구슬이 쌓인 모습이 점점 가운데가 높아지면서 선명해 집니다.
구슬하나를 굴리는 것을 시행(Event)라 할 수 있고 구슬이 들어가는 아래 칸을 표본공간(Sample Space)라고 할 수 있습니다. 하나의 구슬을 굴려서 하나의 칸에 들어가는 가면 하나의 표본(Sample)이 생성된 것이라고 할 수 있습니다. 그리고 여기서 분기점에서 우측으로 가는 확률을 P라 한다면 좌측으로 가는 확률은 (1-P)가 됩니다. 그렇다면 갈톤보드는 좌나 우로 여러번 가는 시행의 결과를 합친 결과를 보여주는 장치입니다.
갈톤보드에서 굴리는 구슬의 수를 크게 해본다면 어떤 결과가 나올까요? 하나의 예로 분기수를 8개로하고 구슬의 수를 크게 하면 구슬더미는 종모양을 점점 가지게 됩니다. 이 구슬더미의 모양을 확률분포로 본다면 그 확률분포를 이항분포(Binomial distribution)라 부릅니다. 이항분포는 분기점의 수(N)와 우측으로 가는 확률(P)로 정해집니다. 여기서 확률변수(Random variable)는 아래 칸이 됩니다. 아래칸에 숫자가 적혀 있으면 수치형 확률변수가 되고 수치가 아니면 명목형 확률변수가 됩니다.
갈톤보드의 분기수를 크게 늘리면 구슬은 가운데로 모이는 모습을 볼 수 있습니다. 이것은 중심극한정리(Central Limit Theorem)를 잘 표현합니다. 또한, 구슬 하나를 분기수가 무한대인 갈톤보드에 굴리면 가운데 칸으로 점점 접근하게 됩니다. 이것은 중심극한정리와 큰수의 법칙을 동시에 잘 표현한다고 볼 수 있습니다.
갈톤보드에서의 구슬굴리기를 여러개의 동전던지기와 연결해보면 동전하나는 갈톤보드의 분기점과 같은 역할을 하고 따라서 분기점수는 동전의 수와 같습니다. 갈톤보드의 결과는 여러개의 동전을 던져서 나온 결과와 연결됩니다.
3. 실습
3.3. 실습강의
갈톤보드 1
갈톤보드 2
두 갈톤보드 비교
4. 용어와 수식
4.1 용어

