2.1 갈톤보드의 확률변수

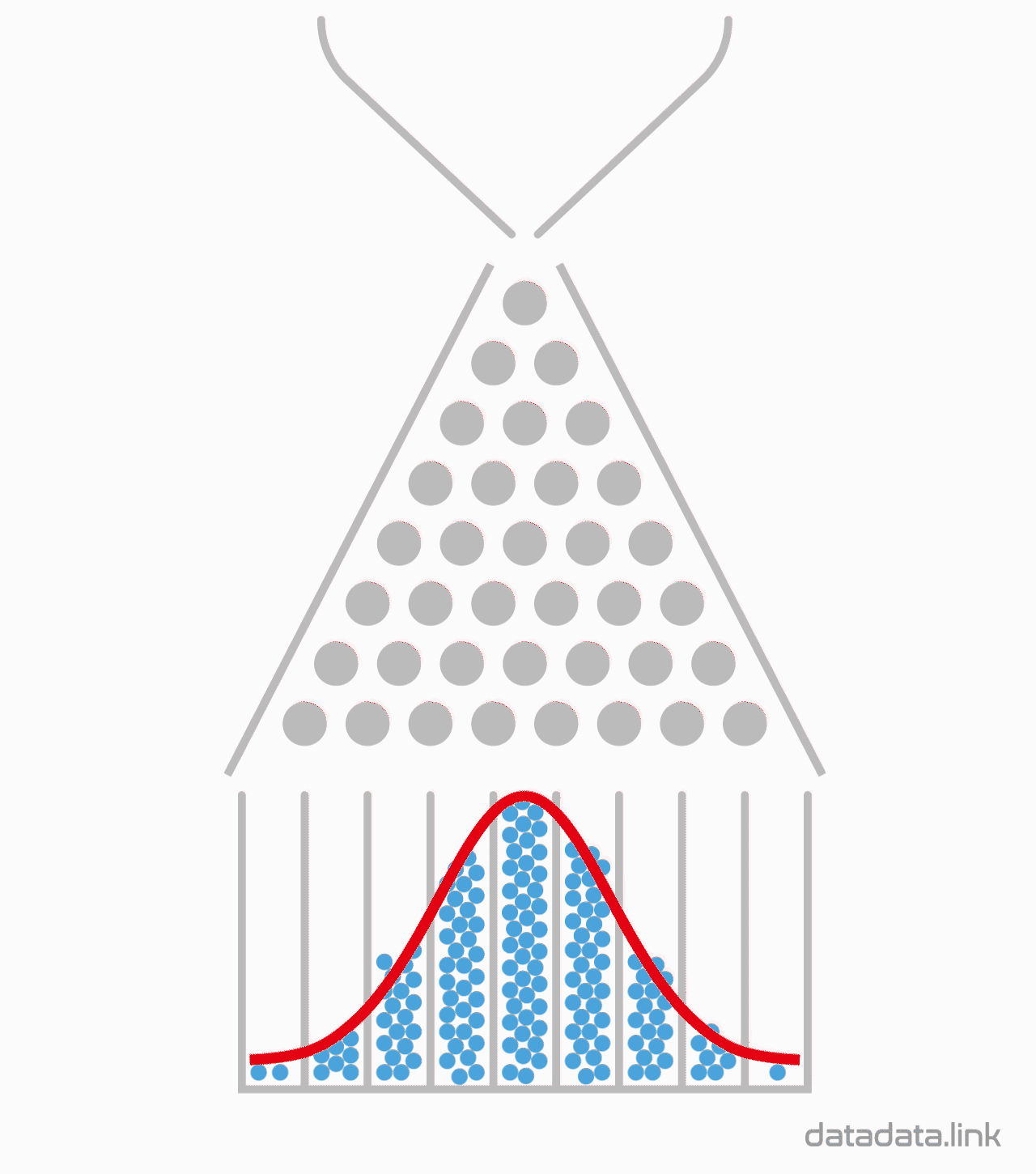
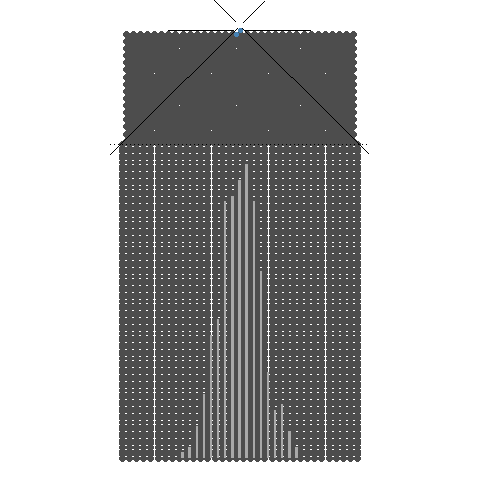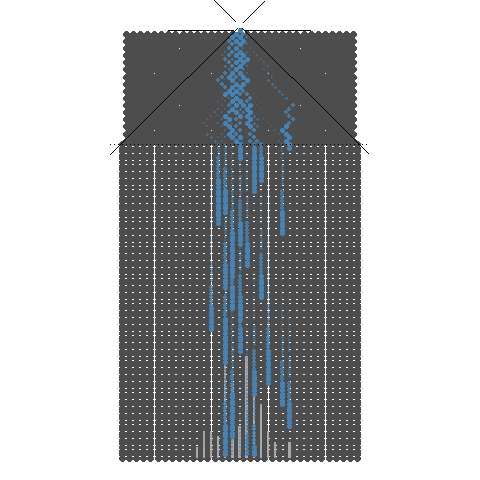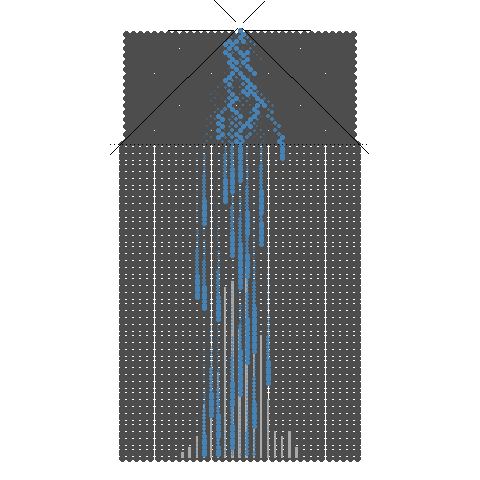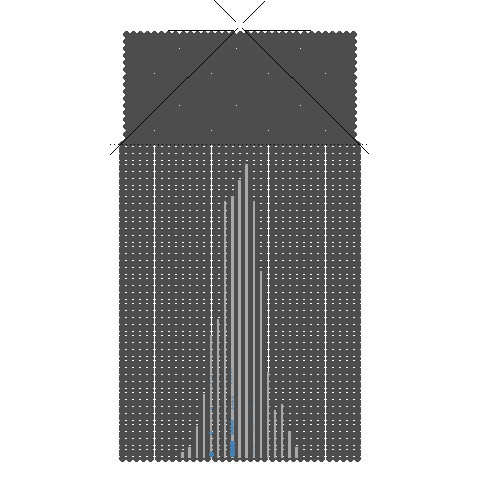
동전던지기처럼 확률을 느껴보는 대표적인 실험으로는 Galton보드가 있습니다. 동전던지기 결과가 동전의 두 면 중에서 한 면을 선택하는 것처럼 갈톤보드는 구슬이 분기점을 지날 때  두 방향 중에서 한 쪽 만을 선택하게 되어 있습니다.

갈톤보드에 구슬을 굴린다는 것은 갈톤보드의 분기점 수 만큼의 동전을 던지는 것과 같은 효과를 냅니다. 동전던지기에서  앞면이 나온 동전의 수와 일치하게 갈톤보드에서 포켓에 번호를 매길 수 있습니다. 예를 들면 동전 4개 던지기는 분기수가 4인 갈톤보드로 생각할 수 있고 갈톤보드 포켓의 번호를 0, 1, 2, 3, 4 로 적는다면 한 개의 구슬이 굴러 들어간 포켓에 적힌 숫자는 4개의 동전을 던질 때 앞면이 나온 숫자와 관련 지을 수 있습니다.

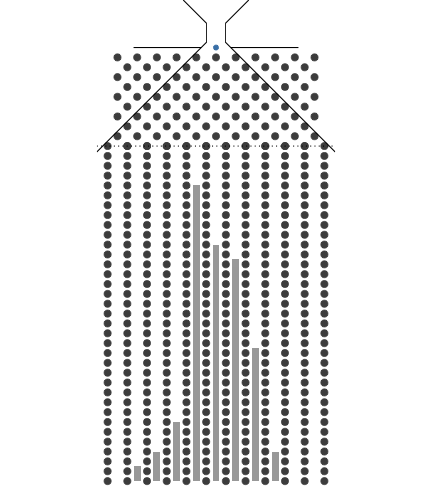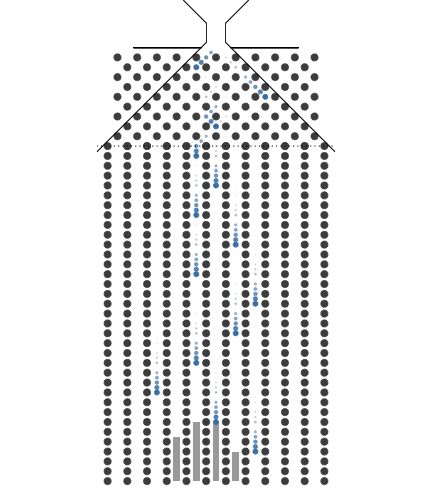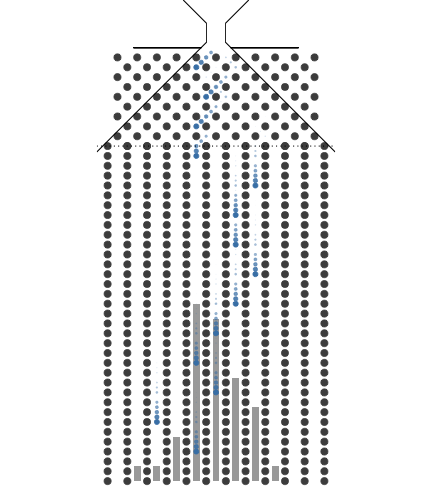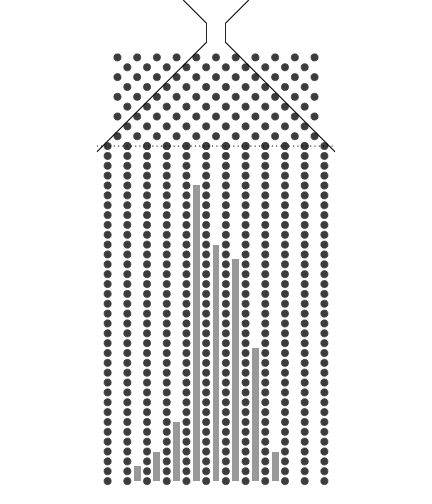
애니메이션에서는  구슬 하나를 분기점이 8개 있는 갈톤보드에 굴리면 동전을 8개 던진 것과 같은 효과가 있음을 보여줍니다. 구체적으로는 동전 8개를 동시에 던져서 나온 1의  합이  8번의 분기점을 가지는 갈톤보드에 1개의 구슬을 굴려 들어간  포켓에 적힌 번호와 같음을 알 수 있습니다. 극단적으로는 8개 동전 모두 1이 나올 경우와 8개 동전 모두 0이 나올 경우가 있습니다. 그리고 8개 동전을 던졌을 때 1이 나올 동전의 숫자는 0부터 8까지이고  경우의 수는 9입니다. 일반화하면  경우의 수는 동전의 수(갈톤보드에서는 구슬이 만나는 분기점의 수) + 1 입니다.

구슬을 여러번 굴린다는 것은 동전던지기를 여러번 한다는 것입니다. 갈톤보드를 사용하면 동전던지기를 한후 나온 앞면의 수를 더하는 수고를 안해도 되는 좋은점이 있습니다. 즉, 여러번 시행을 하면 갈톤보드는 종모양의 분포를 보여줍니다. 이 모양은 도수분포를 의미하며 확률분포라 할 수 있습니다. 여기서 종모양의 확률분포를 이항분포(binomial distribution)라 부릅니다. 

갈톤보드는 두 가지 중 어느 한 쪽을 선택하는 분기의 연속된 수행 결과의 합으로 구성되어 있다고 볼 수 있습니다. 즉,  어느 한 쪽을 선택하는 시행을 지칭하는 베르누이 시행의 반복해서 나온 합의 결과를 표현한다고 할 수 있습니다.

애니메이션에서 같톤보드의 너비를 고정하고 분기 수를 8개와 32개로 늘려 보았습니다. 같은 종모양이지만 분기 수가 클 때 더 가운데에 모이는 것을 볼 수 있습니다. 중심극한정리(Central Limit Theorem)를 시각적으로 보여주고 있습니다.

3.2. 구글시트 함수

=준비 중입니다. 

4.1 용어