표본통계량 ?
Sample statistic ?
1. 애니메이션

표본통계량
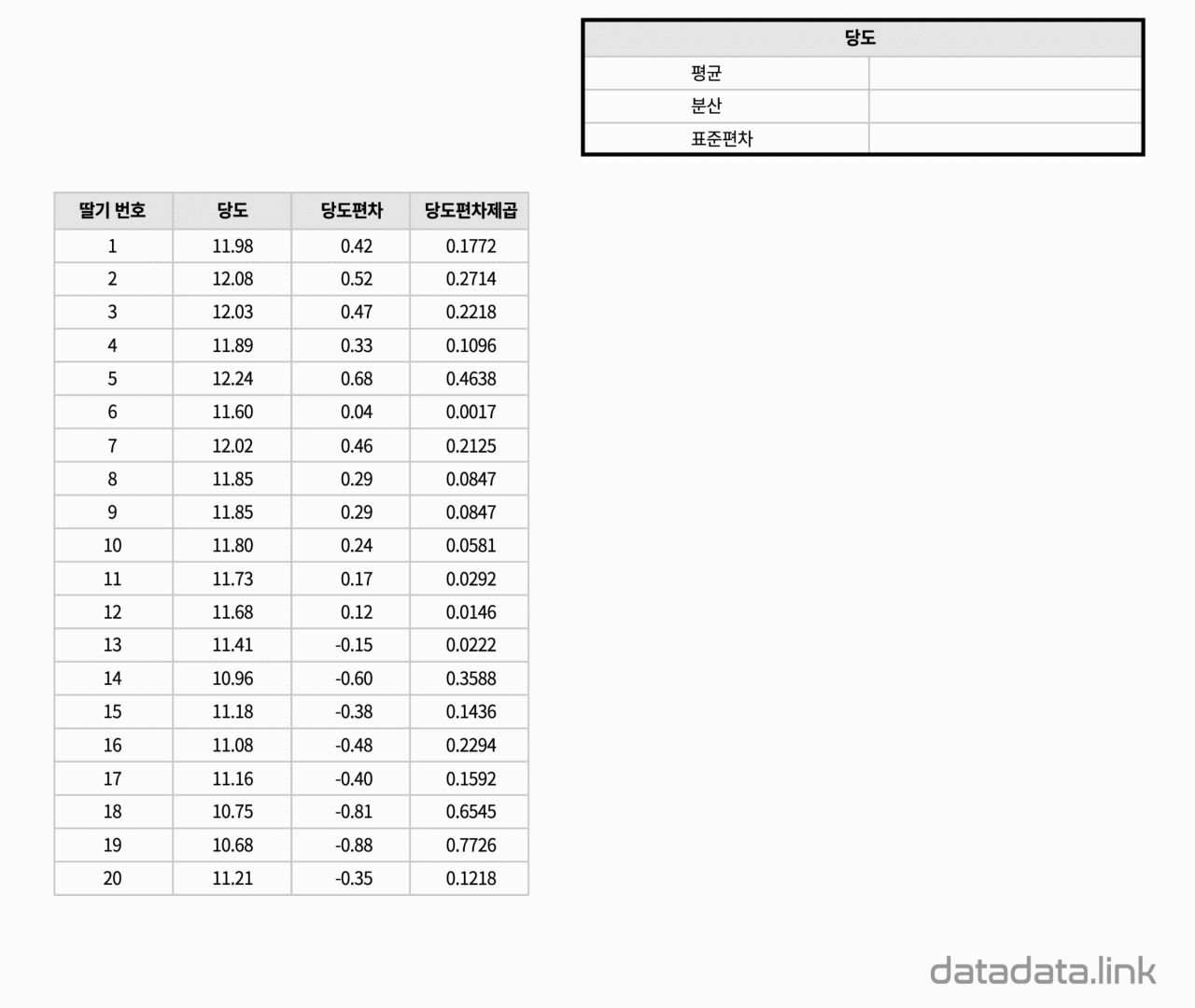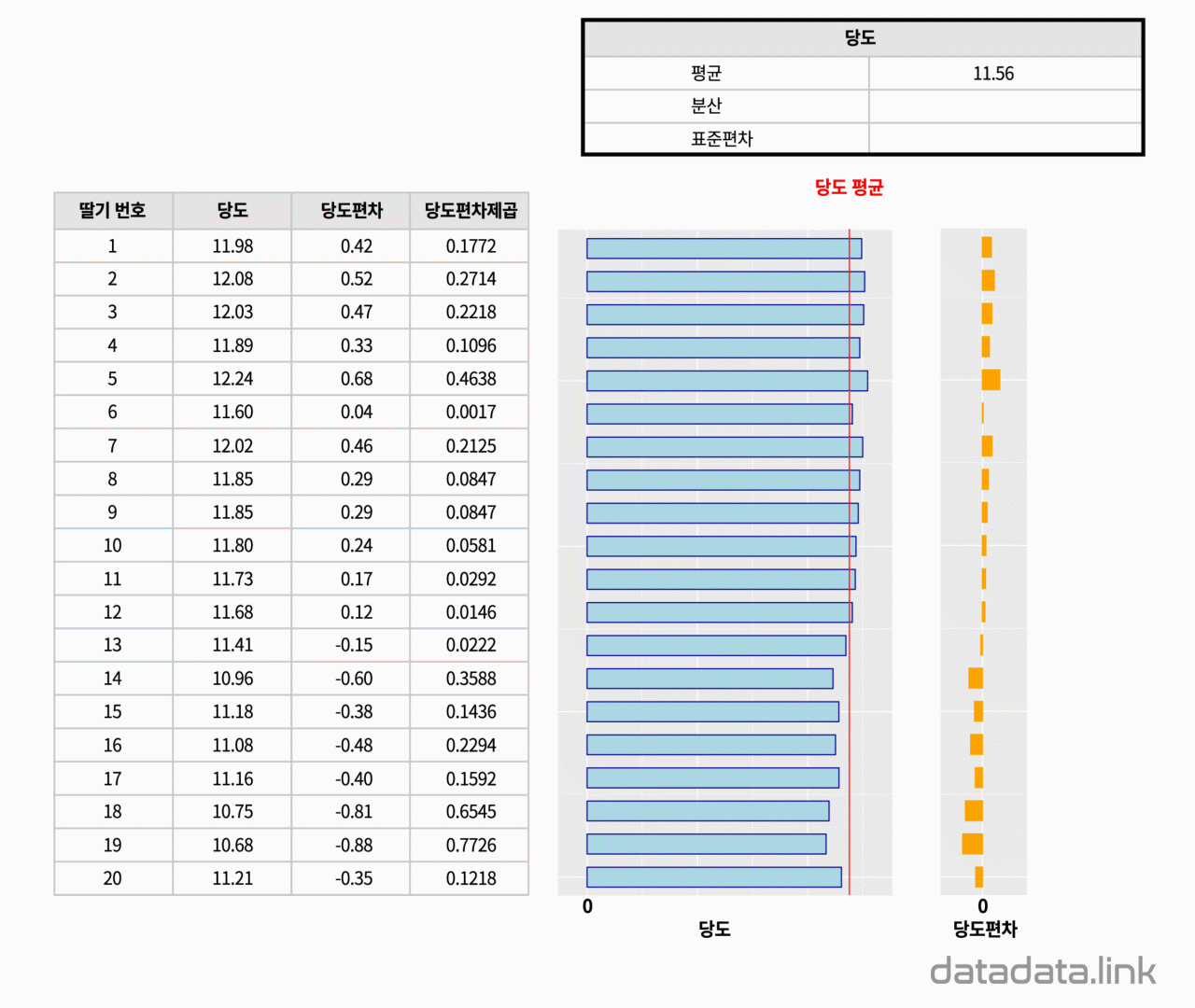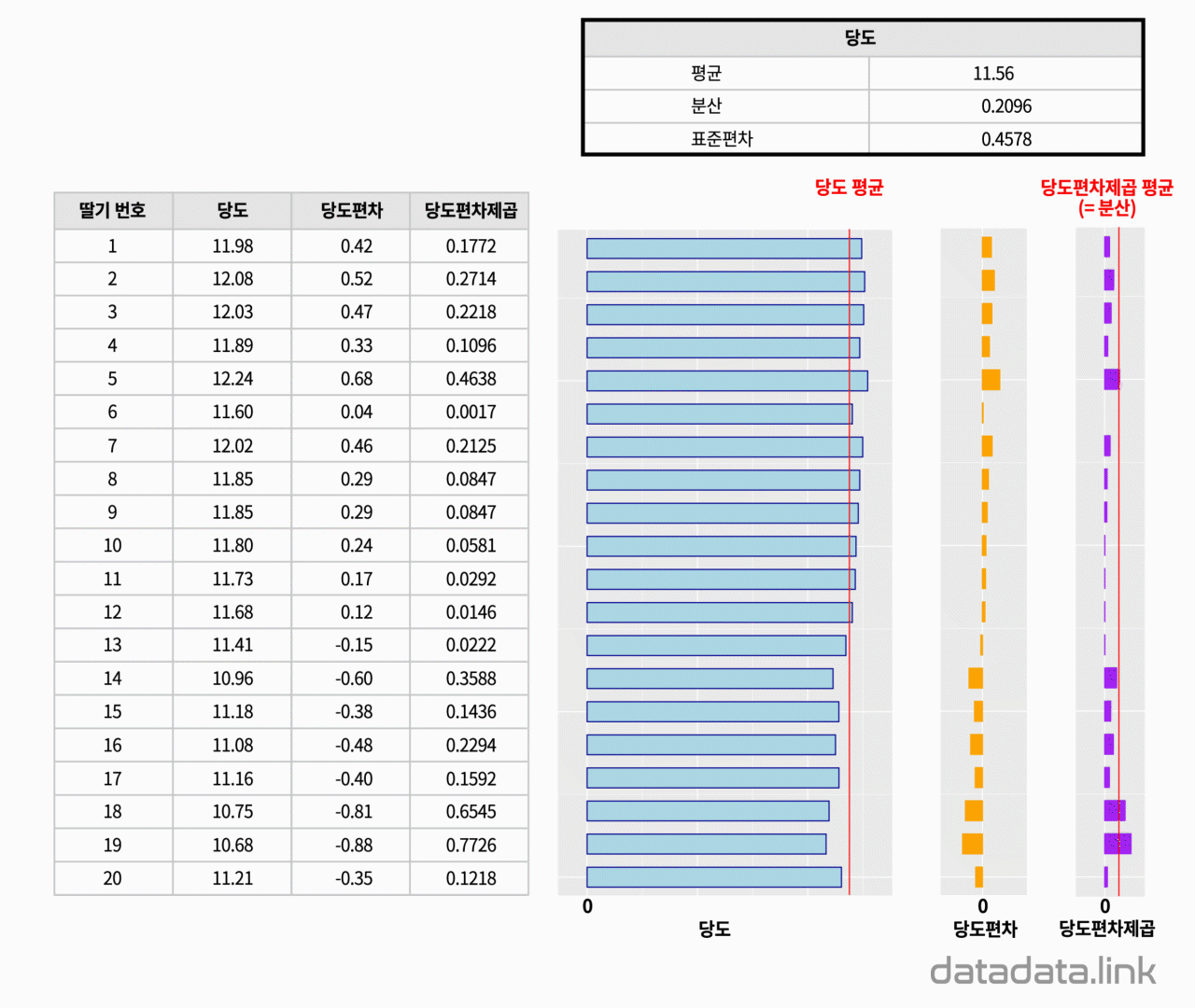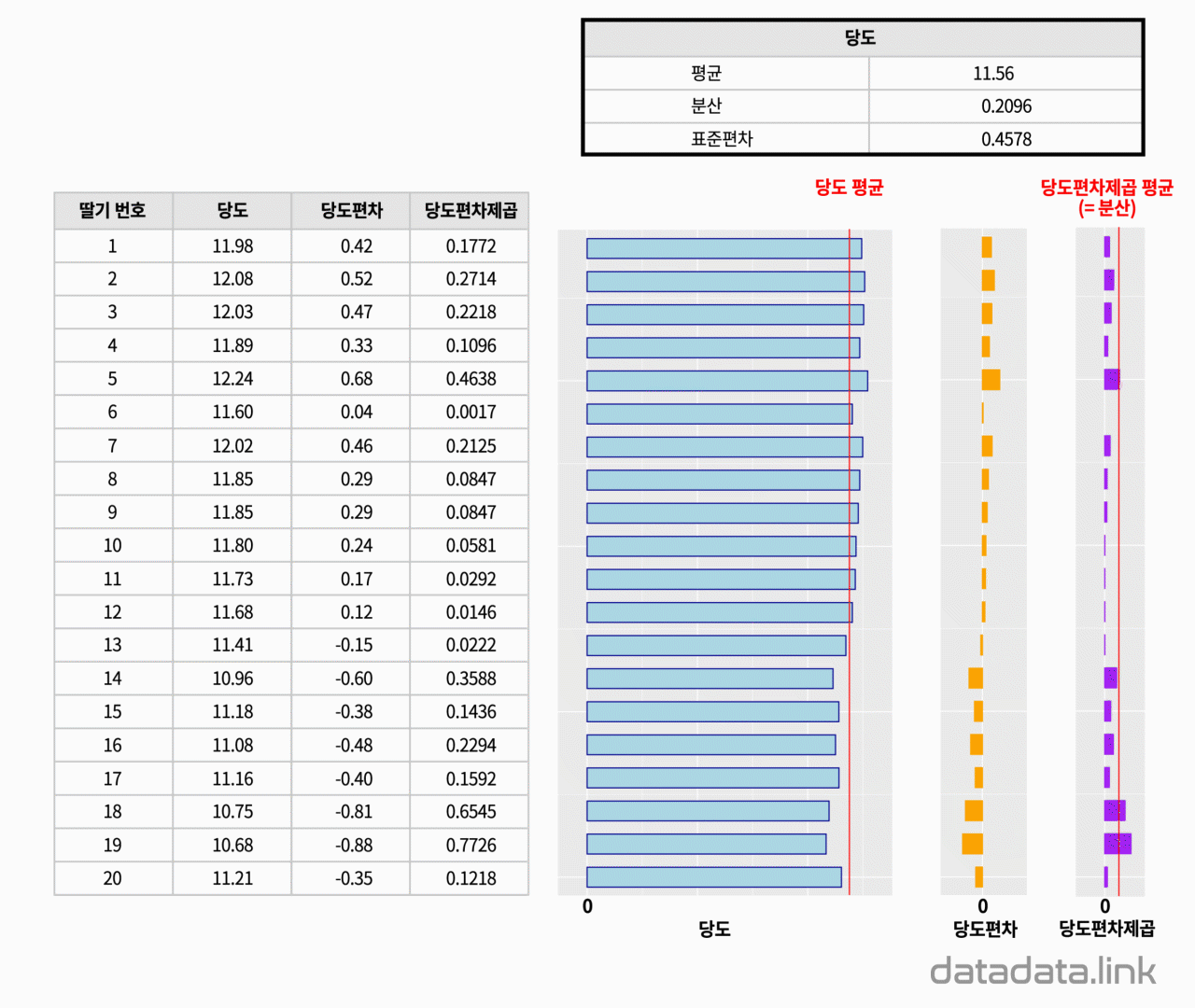
유한집단의 통계량
2. 설명
2.1. 표본의 통계량 : 표본통계량
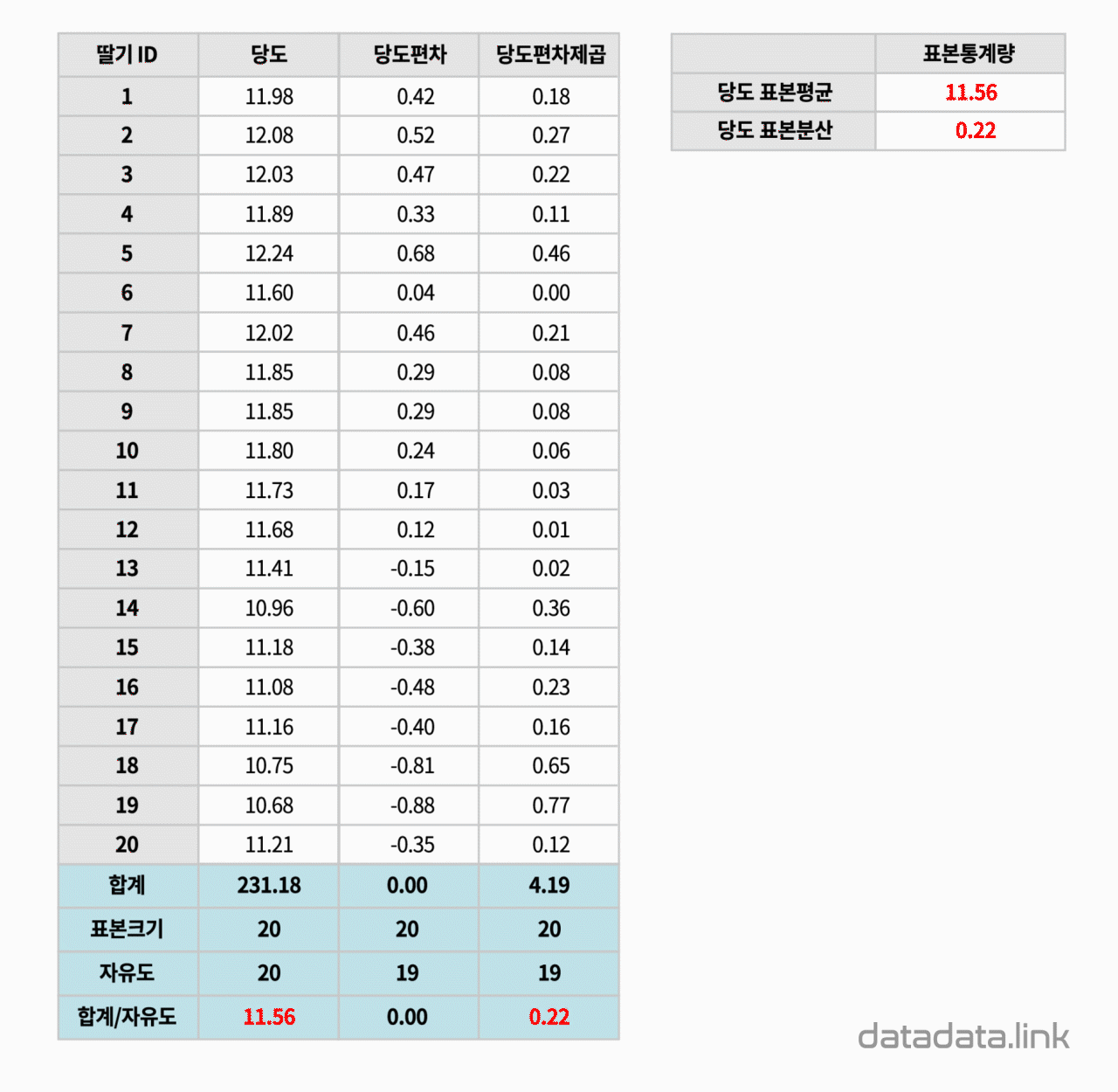
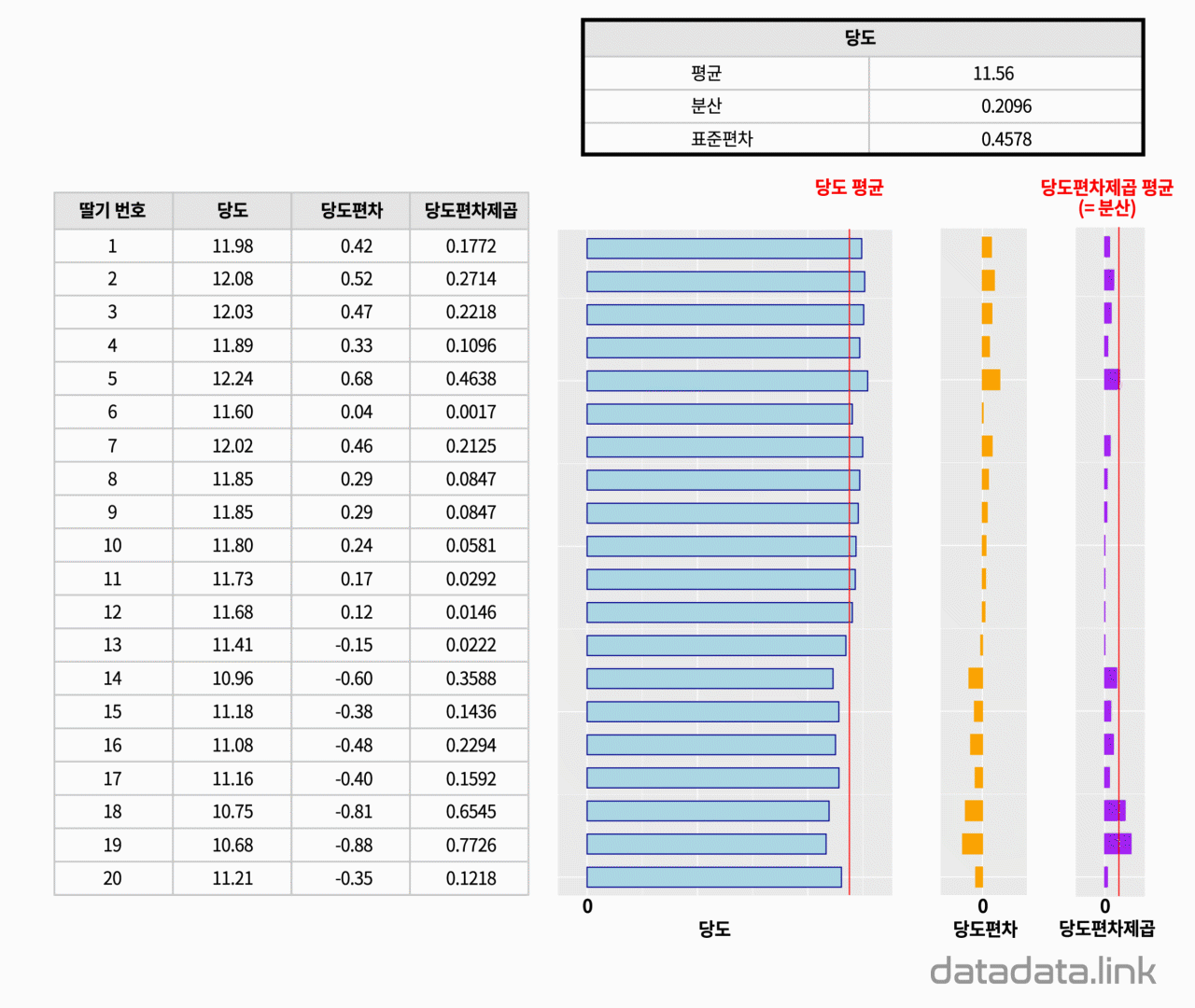
구매한 딸기 포장지에 적혀 있는 당도가 맞는가를 확인하고 싶습니다. 그래서 포장지 속에 들어있는 딸기 20개의 당도를 측정해 보았습니다. 그 결과, 20개의 숫자로 구성된 1개의 숫자무리가 생겼습니다. 이 숫자무리를 우리는 보통 표본이라고 부릅니다. 여기서 표본의 크기는 20입니다. 표본의 개수는 1개입니다.
표본을 표현하는 숫자를 찾는 것을 표본통계량을 구한다고 합니다. 중요한 표본통계량으로는 대표값과 분포값(산포도, 散布度, dispersion)이 있습니다. 대표값은 평균(mean), 중앙값(median), 최빈값(mode)등이 있습니다. 분포의 정도를 나타내는 분포값에는 분산(variance)과 분산의 제곱근인 표준편차(Standard deviation)등이 있습니다.
위의 애니메이션에서 표본의 분산을 계산할 때 표본의 크기에서 1을 뺀 19를 사용하는 것을 볼 수 있습니다. 이것은 표본의 분산을 구할 때 전체 변동량을 표본의 자유도로 나누어 주는데 여기서 표본의 자유도는 표본의 크기에서 기준으로 사용되는 표본평균의 개수인 1을 뺴줍니다.
한편, 포장지에 적혀있는 당도를 모집단의 당도라고 생각해 봅니다. 그리고 측정한 표본 데이터에서 구한 당도 평균과 포장지의 당도를 비교해 봅니다. 포장지에 표시된 당도보다 구매한 당도 표본의 평균이 더 크면 좋겠습니다. 여기서 차이가 표준오차입니다.
무한집단의 예는 딸기품종을 대표적으로 볼 수 있습니다. 한 재배농가의 그 해에 재배한 딸기는 유한집단도 될 수 있지만 재배농가가 선택한 딸기품종의 표본이라고도 할 수 있습니다.
2.2. 집단의 통계량
집단에는 유한집단과 무한집단이 있습니다. 유한집단은 크기가 유한한 집단이고 무한집단은 크기가 무한대인 집단입니다. 집단에서 표본을 추출하면 그 집단은 표본의 모집단이 됩니다. 따라서, 표본의 크기는 집단의 크기보다 작을 수 밖에 없습니다. 집단안에는 부분집단이 있을 수 있으며 부분집단은 집단(group) , 수준(level), 분류(카테고리, category)등으로 불립니다. 집단을 수학적으로 집합으로 표현하여 많은 모델링을 수행합니다. 표본도 관측할 일종의 집단이라고 할 수 있습니다.
표본
표본통계량
표본크기 : $n$
최소값 : $min$
1사분위수: $Q_1$, 25% 백분위수
2사분위수 : $Q_2$, 50% 백분위수, 중앙값($m$)
3사분위수 : $Q_3$, 75% 백분위수
최대값 : $max$
표본평균 : $\bar{X}$
표본분산 : $s^2$
표본표준편차 : $S$
표본피어슨상관계수 : $r$
표본회귀계수 : $\hat{\beta_0}$, $\hat{\beta_1}$, … , $\hat{\beta_p}$ : $p$는 원인변수의 개수
표본기울기 : $\hat{\beta_1}$, … , $\hat{\beta_p}$ : $p$는 원인변수의 개수
표본절편 : $\hat{\beta_0}$
유한집단
유한집단통계량
집단크기 : $N$
최소값 : $min$
1사분위수: $Q_1$, 25% 백분위수
2사분위수 : $Q_2$, 50% 백분위수, 중앙값($m$)
3사분위수 : $Q_3$, 75% 백분위수
최대값 : $max$
모평균 : $\mu$
모분산 : $\sigma^2$
모표준편차 : $\sigma$
모상관계수 : $\rho$
모회귀계수 : $\beta_0$, $\beta_1$, … , $\beta_p$ : $p$는 원인변수의 개수
모기울기 : $\beta_1$, … , $\beta_p$ : $p$는 원인변수의 개수
모절편 : $\beta_0$
무한집단
무한집단통계량
집단크기 : $N \rightarrow \infty$
최소값 : $min$
1사분위수: $Q_1$, 25% 백분위수
2사분위수 : $Q_2$, 50% 백분위수, 중앙값($m$)
3사분위수 : $Q_3$, 75% 백분위수
최대값 : $max$
모평균 : $\mu$
모분산 : $\sigma^2$
모표준편차 : $\sigma$
모상관계수 : $\rho$
모회귀계수 : $\beta_0$, $\beta_1$, … , $\beta_p$ : $p$는 원인변수의 개수
모기울기 : $\beta_1$, … , $\beta_p$ : $p$는 원인변수의 개수
모절편 : $\beta_0$
2.3. 표본모형
랜덤하게 생성(추출)된 표본모형
{$X_1, … , X_n$}
여기서, $X_1, … , X_n$은 서로 독립
$n$은 표본크기
표본의 관측된 값
$x_1, … , x_n$
여기서, $n$은 표본크기
2.4. 표본통계량
표본평균
$\bar {X}=\dfrac {1}{n}\sum\limits _{i=1}^{n}{X_{i}}=\dfrac {X_{1}+X_{2}+\cdots +X_{n}}{n}$
여기서, 표본은 {${X}_{1}{,}{X}_{2}{,}\ldots{,}{X}_{n}$}
$n$은 확률변수 $X$에서 생성(추출)된 표본이 $n$개의 원소로 이루어짐을 의미
표본평균의 관측값
$$\bar {x}=\dfrac {1}{n}\left(\sum _{i=1}^{n}{x_{i}}\right)=\dfrac {x_{1}+x_{2}+\cdots +x_{n}}{n}$$
여기서, 표본의 관측값은 ${x}_{1}{,}{x}_{2}{,}\ldots{,}{x}_{n}$
$n$은 표본이 $n$개의 데이터로 이루어짐을 의미
표본평균의 기대값
$${\rm E}[\bar X] = \mu$$
여기서, $\bar X$는 표본평균
$\mu$는 모평균
모평균의 점추정
$$\mu ∼ {\rm E}[\bar X]$$
여기서, $\bar X$는 표본평균
$\mu$는 모평균
~는 점추정
표본분산
$$S^2=\dfrac {1}{n-1}\sum _{i=1}^{n}\left(X_{i}-{\bar {X}}\right)^2$$
여기서, $n$은 표본의 크기
$\bar {X}$는 표본평균
표본분산의 관측값
$$ s^2=\dfrac {1}{n-1}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^2$$
여기서, $n$은 표본의 크기
$\bar {x}$는 표본평균의 관측값
표본분산의 기대값
$${\rm E}[S^2] = \sigma^2$$
여기서, $S^2$는 표본분산
$\sigma^2$는 모분산
모분산의 점추정
$$\mu ∼ {\rm E}[S^2] = \sigma^2$$
여기서, $S^2$는 표본분산
$\sigma^2$는 모분산
~는 점추정
표본표준편차
$$S=\sqrt {\dfrac {1}{n-1}\sum _{i=1}^{n}\left(X_{i}-{\bar {X}}\right)^{2}}$$
여기서, $n$은 표본크기
$\bar {X}$는 표본평균
표본표준편차의 관측값
$$s=\sqrt {\dfrac {1}{n-1}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}$$
여기서, $n$은 표본크기
$\bar {x}$는 표본평균의 관측값
중앙값(median)
$n$이 홀수인 경우
중앙값 = $\dfrac{n+1}{2}$번째 데이터
$n$이 짝수인 경우
중앙값 = $\dfrac{n}{2}$번째와 $\dfrac{n+1}{2}$번째 데이터의 평균
여기서, $n$은 표본크기 또는 유한집단크기
최빈값(mode)
최빈값 = 데이터 중 가장 자주 나타나는 값
변동계수(coefficient of variation, 변이계수)
모변동계수$(CV)$ : 단위는 %
$$CV=\dfrac{\sigma}{\mu}\times 100$$
여기서, $\mu$은 모평균
$\sigma$은 모표준편차
표본변동계수$(CV)$ : 단위는 %
$$CV=\dfrac{S_Y}{\bar Y}\times 100$$
여기서, $\bar Y$은 확률변수 $Y$의 표본평균
$S_Y$은 확률변수 $Y$의 표본표준편차
범위(range)
범위 = 최대값 – 최소값
범위는 데이터의 최대값과 최소값의 차이
백분위수(percentile)
$p$% 백분위수 = 자기값 이하로 적어도 $p$%의 관측값이 있고 자기값 이상으로 적어도 $(1-p)$%의 관측값이 있는 수
사분위수범위(interquartile range, IQR)
일사분위수(1st quartile, $Q_1$)
$Q_1$ = 25% 백분위수
이사분위수(2nd quartile, $Q_2$)
$Q_2$ = 50% 백분위수 : 중앙값( $m$)
삼사분위수(3rd quartile, $Q_3$)
$Q_3$ = 75% 백분위수
사분위수범위($\mathrm{IQR}$)
$$IQR = Q_3-Q_1$$
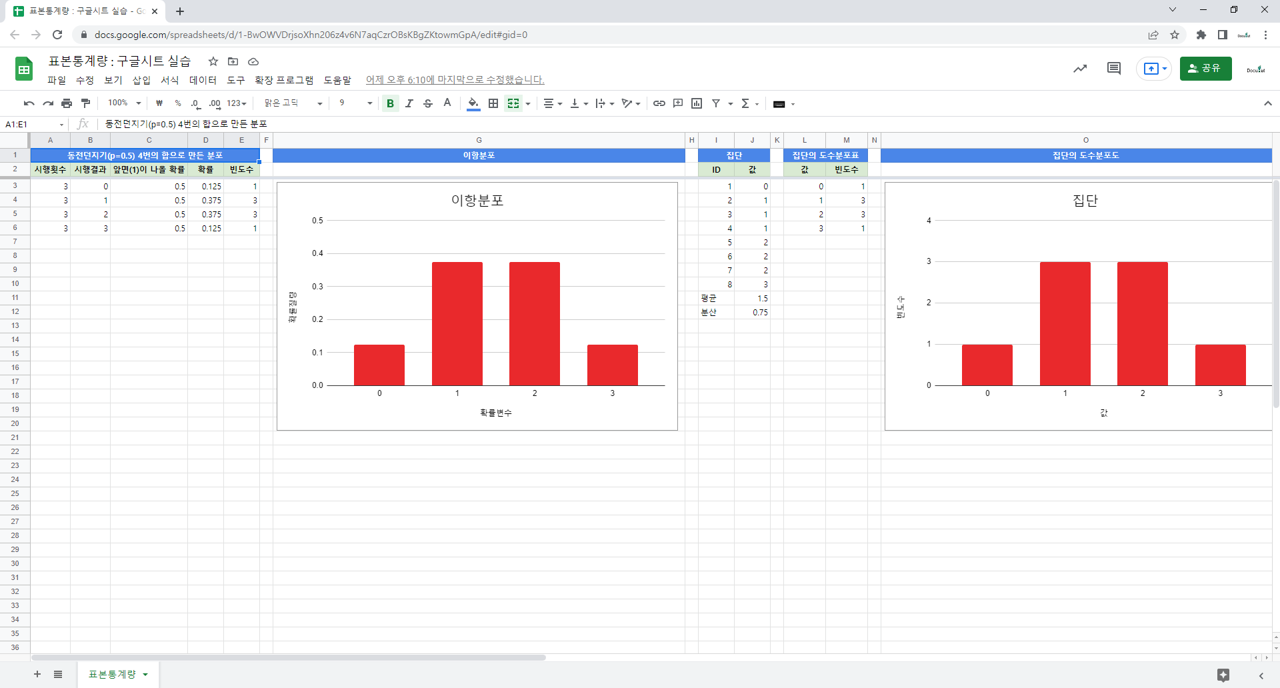
3. 실습
3.2. 구글시트 함수
=FACT(A3) : 숫자의 계승. A3에 있는 숫자의 계승을 계산함. 예를 들어, A3에 있는 숫자가 2이면, 2×1(2곱하기 1)의 값을 계산해서 표시함. A3에 있는 숫자가 3이면, 3×2×1(3곱하기2곱하기 1)의 값을 계산해서 표시함.
=POWER(C3,B3) : 거듭제곱. C3의 값을 B3의 값만큼 거듭제곱한 값을 계산해서 표시함.
=SQRT(D3) : 제곱근. D3에 있는 값의 제곱근을 계산해서 표시함.
=COUNTIF(J3:J10,L3) : 범위에서 조건에 맞는 개수. J3에서 J10에서 L3의 값을 가진 데이터의 개수를 표시함. $표시를 알파벳 앞뒤로 넣으면, 셀을 복사해도 그 값이 바뀌지 않음.
=AVERAGE(R3:S3) : 평균. R3에서 S3에 있는 데이터의 평균을 계산해서 표시함.
=SUM(W3:W7) : 합계. W3에서 W7에 있는 데이터의 합계를 계산해서 표시함.
=VARP(R3:S3) : 모분산. R3에서 S3에 있는 데이터의 모분산을 계산해서 표시함. 편차제곱합을 데이터의 개수로 나눠서 구함.
=VAR.S(R3:S3) : 표본분산. R3에서 S3에 있는 데이터의 표본분산을 계산해서 표시함. 편차제곱합을 (데이터의 개수-1)로 나눠서 구함.
3.3. 실습강의
– 이항분포
– 이항분포에서 실현된 집단
– 집단의 부분집합
– 표본평균
– 표본분산
4. 용어
4.1 용어
기대값
확률에서 임의 변수의 기대값은 직관적으로는 동일한 실험을 무한 반복했을 때 나온 값들의 평균값입니다. 예를 들어, 6면 주사위를 던지는 시행의 기대값은던진 횟수가 무한대에 가까워졌을 때의 결과값들의 평균값(이경우는 3.5)이 됩니다. 다시 말해, 큰 수의 법칙은 반복 횟수가 무한대에 가까워질수록 값의 산술평균은 기대값에 점점 수렴한다는 것을 의미합니다. 이 기대값은 기대치, 수학적 기대치, EV, 평균, 평균값이라고도 불립니다.
보다 현실적으로, 이산확률변수의 기대값은 모든 가능한 값의 가중평균입니다. 즉, 기대값은 확률변수가 취할 수 있는 각 값에 발생확률을 곱한 결과값들의 합이 됩니다. 연속적인 확률변수에 대해서는 합계 대신에 변수의 적분이 들어간다는 것 외에는 동일한 원칙이 적용됩니다. 공식적인 정의는 이 둘을 모두 포함해 이산적이거나 완전히 연속적이지 않은 분포에서도 같게 작용되어, 확률변수의 기대값은 간단히 “확률 측정값에 대한 변수의 적분 값”으로도 말할 수 있습니다.
기대값은 큰 꼬리가 있는 분포(예를 들어 Caushy 분포)에서는 존재하지 않습니다. 이런 무작위 변수의 경우에는 분포의 긴 꼬리가 합이나 적분값이 수렴하지 못하도록 합니다. 기대값은 위치 매개 변수의 한 유형으로 사용할 수 있기 때문에 확률 분포를 특징 짓는데 중요한 역할을 합니다. 그에 반해, 분산은 기대값 주위의 확률변수의 가능한 값들이 얼마나 퍼져 있는 지를 나타내는 값입니다. 분산은 크게 2가지 방법으로 구할 수 있습니다. 모든 값에 평균을 빼고 제곱을 해 평균을 구하거나, 모든 값의 제곱의 평균에 평균의 제곱을 빼서 구할 수 있습니다.
Reference
사분위 범위
사분위 범위 (Interquartile Range, IQR)는 75 ~ 25 백분위 수 또는 상위 및 하위 사분위의 차이로 통계적 분산의 척도입니다. 사분위 범위(IQR)은 “IQR = Q3 – Q1” 식으로 구합니다. 즉, IQR은 3분위수에서 1분위수를 뺀 것입니다. 이 4분위수는 데이터의 상자그림에서 명확하게 볼 수 있습니다. 그것은 정리된 추정량이며 25 % 정리된 범위로 정의되고 일반적으로 사용되는 강력한 통계적 분산의 척도입니다.
IQR은 데이터세트를 사분위수로 나누는 것에 기반한 변화(분포, 가변성)의 척도입니다. 사분위수는 순위가 지정된(내림차순이나 오름차순으로 정리된) 데이터 세트를 네 부분으로 나눕니다. 파트를 분리하는 값을 1, 2, 3 분위수라고 부릅니다. 각각 Q1, Q2, Q3으로 표기합니다.
Reference
Interquartile range – Wikipedia
산술평균
확률과 통계에서 데이터의 평균은 보통 산술평균을 의미합니다. 산술평균 (기대값)은 중심값으로서 데이터 값의 합을 데이터 수로 나눈 값입니다. 숫자 집합 x1, x2, …, xn의 산술평균은 일반적으로 “엑스 바(X bar)”라고 발음되는 $\bar {X}$로 표시됩니다. 집단의 모평균($\mu$ 또는 $\mu_{X}$로 표시)은 “뮤”라고 발음합니다. 집단에서 추출하여 얻은 여러 개의 표본의 산술평균을 집단의 표본평균 ($\bar {X}$)의 표집(Sample distribution)이라고 부릅니다.
확률 및 통계에서 집단의 모평균(기대값)은 확률분포 또는 그 분포로 특정되는 확률변수의 중심을 표현하는 대표적인 척도입니다. 확률변수 $X$의 이산확률분포의 경우, 평균은 그 값의 확률로 가중치화된 모든 값의 합과 동일합니다. 즉, $X$의 가능한 값 $x$와 그 확률$p (x)$의 곱을 취한 다음 이들을 모두 합하여 구합니다. $ \mu = \sum xp(x)$. 연속확률 분포의 경우에도 유사한 공식이 적용됩니다. 예를 들어, 구성원의 평균 키는 모든 구성원의 키를 합하여 전체 개체 수로 나눈 값과 같습니다. 모든 확률분포에 정의된 평균이 있는 것은 아닙니다. 예를 들어 Cauchy 분포입니다.
집단의 표본평균은 집단의 모평균과 다를 수 있으며, 특히 표본크기가 작을수록 경우집단의 표본평균과 모평균은 다를 가능성이 높아집니다. 큰 수의 법칙은 표본의 크기가 클수록 집단의 표본평균이 집단의 모평균에 가까울 확률이 높다는 것을 나타냅니다.
Reference
범위
데이터 범위는 가장 큰 값과 가장 작은 값의 차이입니다. 구체적으로 데이터세트의 범위는 가장 큰 값에서 가장 작은 값을 뺀 결과 값입니다. 그러나 설명통계(기술통계)에서 범위개념은 보다 복잡한 의미를 지닙니다. 범위는 모든 데이터를 포함하고 통계적 분산의 표시를 제공하는 최소 간격의 크기입니다. 그것은 데이터와 동일한 단위로 측정됩니다. 최대값, 최소값 두 값만으로 표현되기 때문에 표본크기가 작은 데이터세트의 분산을 표현하는 데 가장 유용합니다.
Reference
Range (statistics) – Wikipedia
표준편차
표준편차(모표준편차는 $\sigma$, 표본 표준편차는 $S$를 기호로 사용)는 데이터 값의 다양성이나 분포를 나타내는 척도입니다. 표준편차가 작다는 것은 데이터 값들이 대략적으로 평균(기대값)에 가까이 분포한다는 것을, 표준편차가 높다는 것은 평균에서 멀리 분포한다는 것을 의미합니다.
확률변수, 통계적 집단, 데이터의 무한집합 또는 확률분포의 모표준편차는 모분산의 제곱근입니다. 절대편차의 평균보다 정확하지는 않지만 수학의 대수적인 면에서 더 간단합니다. 표준편차가 가지는 장점은 분산과 다르게 데이터와 같은 단위를 사용한다는 것입니다.
표준편차는 집단의 분포정도(분산도)를 표현하기 위한다는 것 외에도 통계적 결론에 대한 신뢰도를 측정하는 데에도 사용됩니다. 예를 들어, 투표 데이터의 오류 허용 범위는 투표가 여러번 진행되었을 때 기대되는 표준편차를 계산하여 구하게 됩니다. 이 표준편차의 활용은 추정치의 표준오차, 또는 평균값의 표준 편차라고 부릅니다. 무한한 수의 표본이 추출되고 각 표본의 평균이 계산될 경우 그 집단에서 추출될 수 있는 모든 표본에서 계산되는 표본평균의 표준편차를 표본평균 표집의 모표준편차로 부릅니다. 즉, 표본평균의 표집의 모표준편차가 통계적 결론(모평균 점추정)에 대한 신뢰도로 나타납니다.
집단의 모표준편차과 집단에서 추출한 표본에서 구한 표본평균의 표준오차는 서로 다르면서도 연관되어 있다는 것(관측 수의 제곱근과 관련됨)이 매우 중요합니다. 관찰된 오류는 표본평균의 표준 오차(집단의 모표준편차에 표본크기의 제곱근의 역수를 곱한 것)로 계산되며 일반적으로 95% 신뢰구간의 절반, 표준편차의 약 2배(정확하게는 1.96배)입니다.
과학에서는 많은 연구자들이 실험 데이터의 표준편차를 기록한 후, 기대했던 값보다 표준편차의 2배가 넘게 차이가 났을 때에만 통계적으로 의미있다고 판단해 일반적인 무작위적 오류를 배제합니다. 또한 표준편차는 투자 변동성의 척도를 수익률의 표준편차로 계산되는 것처럼 금융에서도 중요합니다.
집단의 데이터 중 일부만 사용이 가능할 경우, “표준편차의 표본” 또는 “표본표준편차” 이 2가지 표현이 모두 위에서 언급한 양 또는 집단의 모표준편차의 편견없는 기대값을 의미할 수 있습니다.
Reference
standard deviation – Wikipedia
분산
확률과 통계에서 분산은 변수와 평균값 간의 편차의 제곱의 기대치입니다. 비공식적으로 분산은 집단 내 숫자가 평균값에서 얼마나 멀리 퍼져 있는지를 나타냅니다. 분산은 통계에서 설명통계, 통계적 추론, 가설검정, 적합성 및 몬테카를로 샘플링 등 많은 곳에 쓰이면서 중심적인 역할을 합니다. 분산은 데이터의 통계 분석이 많이 쓰이는 과학분야에서의 중요한 도구입니다. 분산은 표준편차의 제곱, 분포의 두번째 중심 모멘트, 무작위 변수와의 공분산이며, 집단의 모분산($\sigma ^ 2$), 표본분산($S^2$)이 있습니다 그리고 연산자 이름은 $\mathrm{Var}[X]$로 표현됩니다.
Reference
중앙값
중앙값은 데이터세트(유한집단 또는 표본 또는 이산확률분포)의 하반부와 상반부를 분리하는 값이며 “중간”값으로 간주 될 수 있습니다. 예를 들어, 데이터세트 {1, 3, 6, 7, 8, 9}에서 중앙값은 데이터 집합에서 네 번째로 크고 네 번째로 작은 숫자입니다. 연속적인 확률분포의 경우, 중앙값은 숫자가 상반부 또는 하반부로 정해질 가능성이 같은 값입니다. 중앙값은 통계 및 확률 이론에서 데이터 집합의 속성에 일반적으로 사용되는 척도입니다.
데이터를 요약하거나 설명할 때, 평균에 비해 중앙값의 좋은 점은 매우 크거나 작은 값으로 데이터의 대표값이 왜곡되지 않으므로 더 나은 대표성을 제공 할 수 있습니다, 예를 들어, 평균가계소득이나 평균자산과 같은 통계량을 이해할 때 적은 수의 매우 크거나 작은 데이터로 인해 평균은 극단적으로 왜곡 될 수 있습니다.반면에 가계소득의 중앙값은 “전형적인”수입이 무엇인지를 제시하는 더 좋은 방법 일 수 있습니다.이 때문에 중앙값은 중요한 통계에서 가장 신뢰할 만한 대표값이며 50 %의 분해점을 갖는 가장 믿을 만한 통계량이므로 데이터의 절반 이상이 실제와 다르지 않는 한 중앙값은 크게 달라지지 않습니다.