2.1. 표본통계량으로 집단의 모수 추정

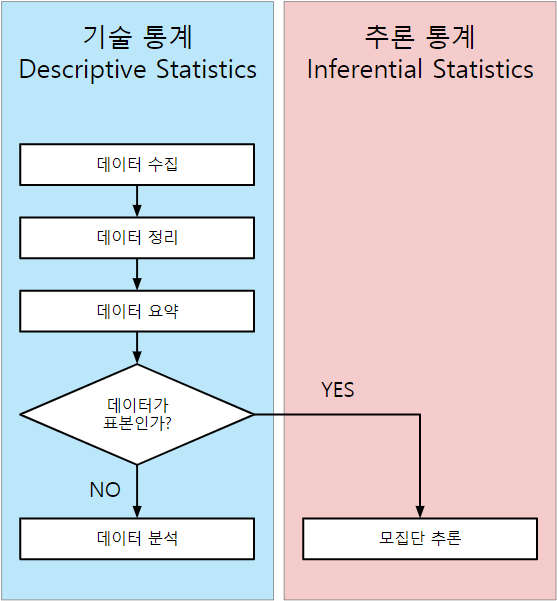
표본으로 표본이 추출된 집단(모집단)을 추론하는 방법을 살펴보면, 첫번째로 표본의 통계량(statistic)인 표본평균, 표본분산을 계산으로 구해서 집단의  모평균, 모분산을 점추정합니다.  두번째로  집단의  통계량(모수, parameter)을 신뢰도(0%~100%)를 밝히고 표본의 통계량을 중심으로 모수가 어디 어디 사이에 있다고 주장하는 것입니다. 이것을 구간추정이라고 합니다.

집단은 연구대상이 되는 집단을 말합니다. 연구집단(목표집단)은 연구조사 목적에따른 개념적 집단입니다. 조사집단은 표본으로 추출가능한 개체들로만 구성된 집단입니다. 모수(parameter)는 집단의 특성을 나타내는 값입니다. 고정된 값이긴 하지만 그 정확한 값은 모릅니다. 그래서 통계적 추론으로 구합니다. 예를 들면 지역별, 세대별 의료비지출 등입니다. 특별히 표본이 추출된 집단을 그 표본의 모집단(population)이라고 부룹니다.

표본(sample)은 표본보다 더 큰 집단의 추론을 위해 수집하고 분석하는 원소(element)의 집합입니다. 즉, 집단의 부분집합입니다. 표본통계량(sample statistics)은 표본으로 부터 계산된 표본평균, 표본분산, 표본비율등을 말합니다.

표본으로부터 표본이 추출된 집단의 특성을 알기위한 방법으로 확률(probability)을 도입합니다. 확률에서 시행과 사건의 개념을 다음과 같이 정리할 수 있습니다.

    * 시행은 관측(조사)행위이다.

    * 사건은 시행의 결과다.

   * 전사건은 시행에서 얻을 수 있는 결과의 모든 집합이다.

    * 근원사건은 모두 같은 정도로 확률을 가지는  더 이상 나눌 수 없는 개별 사건이다.

확률은 수학적 확률과 통계적 확률이 있는데 통계적 확률은 시행을 반복해서 얻을 수 있는 실제를 반영한 확률입니다. 수학적 확률과 통계적 확률이 같은 경우는 통계적 확률에 사용하는 환경이 완벽한 경우입니다. 예를 들면 완벽한 육면체의 주사위를 완벽히 같은 환경에서 던지기를 무한대로 시행하면 통계적 확률과 수학적 확률은 같습니다. 수학적확률은 통계적확률의 환경을 가정하는 방식으로 집단을 모델링한 것입니다.

집단의 속성을 나타내는 모수(parameter)에는 모평균과 모분산등이 있습니다. 표본에서 산출되는 평균과 분산 등을 표본통계량(sample statistic)이라 하며 통계량(statistic)의 복수형(statistics)은 통계(statistics)를 표현합니다. 통계량은 표본을 고르는 방법에 따라 값이 결정되는 확률변수입니다. 따라서 표본통계량은 확률변수이고 대응하는 확률분포를 표집분포(smapling distribution of sample statistic)라 합니다. 표본통계량 중 하나인 표본평균은 모집단에서 추출한 표본의 대표값 중 하나입니다.

정규성을 갖는 집단은 집단의 확률변수가 정규분포라고 가정할 수 있는 특별한 집단입니다. 모평균은 집단(집단의 데이터개수에 따라 데이터개수가 유한한 유한집단과 데이터개수가 무한한 무한집단)의 데이터의 평균을 말합니다. 모분산은 집단의 데이터의 분포정도를 나타냅니다. 집단 전체를 관측하는 것(전수검사)이 힘드므로 모평균, 모분산은  모르는 경우가 많습니다. 표본을 추출하여 모평균, 모분산을 추정하는 것이 추측통계입니다.

2.2. 추정(estimation) : 모수(parameter), 추정량(estimator), 추정값(추정치, estimate)

통계적 실험이나 조사의 목적은 미지의 집단에 대한 정보를 알아보려고 하는 것입니다. 집단의 정보란 대개 평균, 분산 등과 같은 집단의 특성값을 말하며, 이러한 집단의 특성값을 모수(parameter)라고 합니다. 집단 전체를 조사하는 것은 불가능하거나 시간, 경비가 많이 들기 때문에, 대개 모수는 표본을 추출하여 표본평균, 표본분산과 같은 표본의 특성값을 이용하여 추정하게 됩니다.

표본의 특성값을 표본통계량(sample statistic)이라 부르고, 표본통계량의 확률분포를 표집분포(sampling distribution)라 합니다. 표집분포는 표본통계량과 모수 사이의 관계를 규명해 주기 때문에 모수의 추정과 검정을 가능하게 합니다.

모평균은 하나의 값이지만 표본평균은 여러 개의 값을 가질 수 있습니다. 즉, 모평균 $\mu$는 집단의 하나의 대표값인 모수(parameter)라고 부르고 표본평균은 서로 다른 많은 값을 가질 수 있는 확률변수로서 일반적으로 대문자를 사용하여 $\bar{X}$로 표시합니다.  $\bar{X}$를 모수 $\mu$의 추정량(estimator)이라 부릅니다. 한 표본에서 구한 $\bar{X}$의 관측하여 구현된 값을 소문자를 사용하여 $\bar{x}$로 표시하고 이 $\bar{x}$를 $\mu$의 추정값(estimate)이라 부릅니다. 역시, 집단의 모수인 모분산( $\sigma^2$)을 추정하는 추정량은 표본분산 $S^2$입니다. 그 관측값인 $s^2$은 모분산의 추정값(estimate)입니다.

3.2. 구글시트 함수

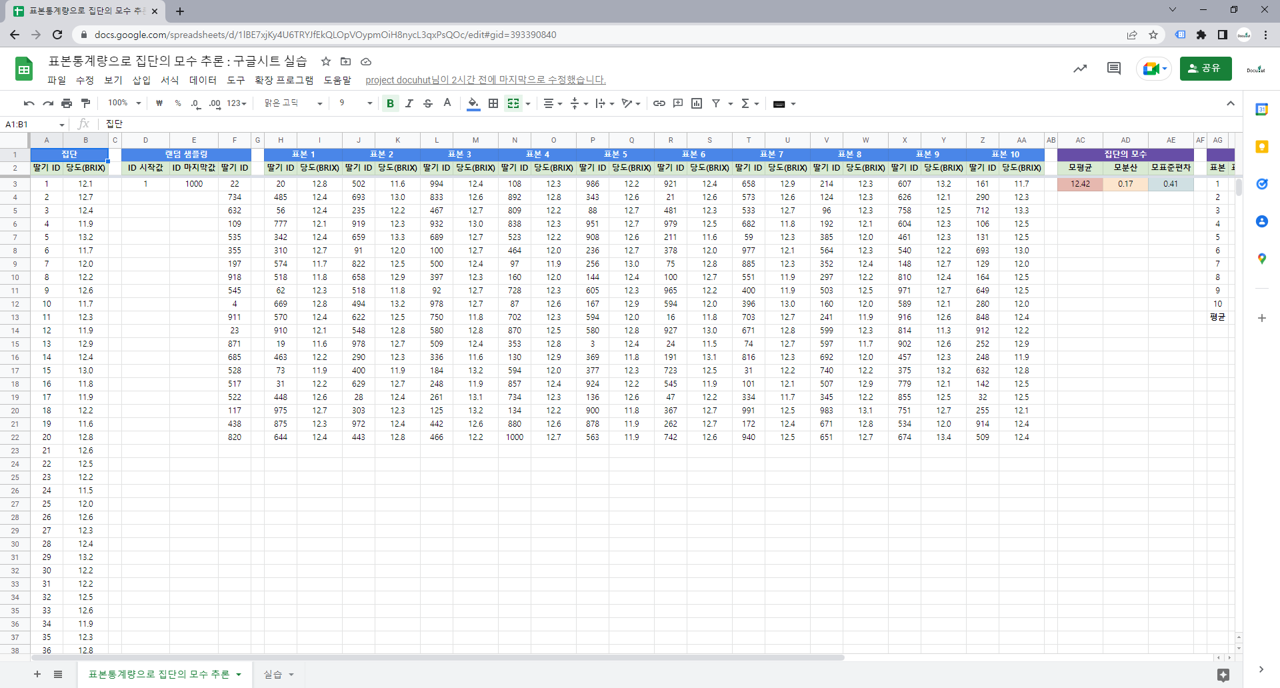
=VLOOKUP(H3,A:B,2,FALSE) : 열 방향 검색. A:B열의 첫 번째 열에서 H3값이 있는 행의 2번째 값을 표시합니다. FALSE를 입력하면, 완전히 일치된 값만 표시합니다. FALSE가 아닌 TRUE를 입력하면, H3에 근접한 값(H3보다 작거나 같은 값)이 있는 행의 2번째 값을 표시합니다.

=AVERAGE(B3:B1002) : 평균. B3에서 B1002에 있는 데이터의 평균.

=VARP(B3:B1002) : 모분산. B3에서 B1002에 있는 데이터의 모분산. 편차제곱합을 데이터 개수로 나눔.

=STDEV.P(B3:B1002) : 모표준편차. B3에서 B1002에 있는 데이터의 모표준편차. 모분산의 제곱근.

=COUNT(I3:I22) : 데이터 개수. I3에서 I22에 있는 숫자로 표시된 데이터의 개수.

=VAR.S(I3:I22) : 표본분산. I3에서 I22에 있는 데이터의 표본분산. 편차제곱합을 데이터 개수 -1로 나눔.

=STDEV.S(I3:I22) : 표본표준편차. I3에서 I22에 있는 데이터의 표본표준편차. 표본분산의 제곱근.

=AK3/SQRT(AH3) : AK3 값을 AH3의 제곱근으로 나눔. 이 실습에서는 표준오차를 계산함.

=T.INV(1-(1-AN3)/2,AH3-1) : T확률분포에서 T값을 계산. T.INV(확률, 자유도)로 구성. 이 실습에서는 AN3에 95% 신뢰수준을 입력하였는데, 양측검정에서는 양쪽 끝 확률이 각각 2.5%가 되어야 함. 따라서, 1-(1-0.95)/2를 하면 누적확률밀도가 0.975, 즉 97.5%가 되어서, 양쪽 끝 확률이 각각 2.5%인 T값을 얻을 수 있음.

=AND(AR3>=AP3, AR3<=AQ3) : 입력된 조건이 모두 참이면 TRUE, 입력된 조건 중 하나라도 거짓이면, FALSE를 표시. AR3값이 AP3 이상이고, AQ3 이하이면 TRUE를 표시함.

4.1 용어