아니요, 변량(확률변수값) 간의 상관이 있어야 합니다.
다변량 정규분포는 정규성과 상관이 있는 확률변수들을 원소로 하는 벡터의 확률분포입니다.
개체의 속성이 정규분포를 나타내고 개체의 속성이 서로 상관을 가질 때 개체가 이루는 집단의 속성의 분포는 확률변수 벡터로 표현되며 그 벡터는 다변량 정규분포를 나타냅니다.
다변량 정규분포를 나타내는 대표적인 확률변수 벡터로는 집단의 육종가 벡터가 있습니다.
\[
\mathbf{a} =
\begin{pmatrix}
a_1 \\
a_2 \\
\vdots \\
a_p
\end{pmatrix}, \quad
\mathbf{a}^\top =
\begin{pmatrix}
a_1 & a_2 & \cdots & a_p
\end{pmatrix}
\]
여기서, $\mathbf{a}$는 표본의 육종가벡터
$\mathbf{a}^\top$는 육종가벡터의 전치
$a_1, a_2, \dots, a_p$는 표본내 각 개체의 육종가
$p$는 표본크기
육종가벡터 $\mathbf{a}$를 다변량 정규분포로 모델링하면 다음과 같습니다.
\[
\mathbf{a} \sim \mathcal{N}(\mathbf{0}, \sigma_a^2 \mathbf{A})
\]
여기서, $\mathbf{a}$는 $p\times1$ 육종가벡터
$\mathbf{0}$는 $p\times1$ 평균벡터: $\mathbf{\mu}=\mathbf{0}$
$\sigma_a^2 \mathbf{A}$는 $p\times p$ 공분산
$\sigma_a^2$는 육종가분산(additive genetic variance): 스칼라양
$\mathbf{A}$는 $p\times p$ 계보행렬
단변량 정규분포는 하나의 확률변수에 대한 분포로 평균과 분산으로 정의됩니다.
$$X \sim \mathcal{N}(\mu, \sigma^2)$$
반면, 다변량 정규분포는 여러 개의 확률변수가 결합된 확률변수 벡터로 평균벡터와 공분산행렬로 정의됩니다. 이 때 변수 간의 상관관계가 공분산행렬에 반영됩니다.
$$\mathbf{X} = (X_1, X_2, \dots, X_p)^\top \sim \mathcal{N}_p(\boldsymbol{\mu}, \boldsymbol{\Sigma})$$
여기서, $\boldsymbol{\mu}$는 평균벡터: $\boldsymbol{\mu} \in \mathbb{R}^p$
$\boldsymbol{\Sigma}$는 분산행렬: $\boldsymbol{\Sigma} \in \mathbb{R}^{p \times p}$
Table 1. 단변량 정규분포와 다변량 정규분포 비교
| 항목 | 단순한 정규분포의 합 | 다변량 정규분포 |
|---|---|---|
| 구성 | 독립된 정규분포 여러 개 | 상호 연관된 정규변수 |
| 상관관계 | 없음 (공분산 = 0) | 존재할 수 있음 (공분산 ≠ 0) |
| 형태 | 각 변수는 서로 무관 | 변수 간 공분산행렬로 상호 의존 |
| 예시 | \( X_1 \sim N(0,1),\ X_2 \sim N(5,4) \), 독립 | \( (X_1, X_2) \sim \mathcal{N}_2(\boldsymbol{\mu}, \boldsymbol{\Sigma}) \), 공분산 존재 가능 |
다변량 정규분포 $\mathbf{x} \sim \mathcal{N}_p(\boldsymbol{\mu}, \Sigma)$의 확률밀도함수는 다음과 같습니다.
\[
f(\mathbf{x}) = \frac{1}{(2\pi)^{p/2} |\boldsymbol{\Sigma}|^{1/2}}
\exp\left( -\frac{1}{2} (\mathbf{x} – \boldsymbol{\mu})^\top
\boldsymbol{\Sigma}^{-1} (\mathbf{x} – \boldsymbol{\mu}) \right)
\]
여기서, $p$는 변수의 개수
$|\boldsymbol{\Sigma}|$는 공분산행렬의 행렬식(determinent)
$\boldsymbol{\Sigma}^{-1}$는 공분산행렬의 역행렬
공분산행렬 $\Sigma$는 각 변수의 분산(대각원소)과 변수 간의 공분산(비대각원소)을 담고 있어 분포의 형태, 회전, 확산 정도를 결정합니다. 또한, 등고선(확률밀도 등치선)은 타원형을 가지며, 그 타원의 방향과 크기를 공분산행렬이 결정합니다.
확률밀도함수의 등고선은 중심이 $\mathbf{\mu}$인 타원(Ellipse)이며, 그 타원의 크기와 방향은 공분산행렬의 고유값과 고유벡터에 의해 결정됩니다. 고유벡터는 타원의 주축 방향을, 고유값은 타원의 축 길이를 결정합니다.
1. 부분집합 또는 선형결합도 정규분포입니다.
다변량 정규분포에서 일부 변수만 추출하거나 선형결합 $\mathbf{Z}^top\mathbf{a}$를 구성하면 그것 또한 정규분포를 따릅니다. 즉, 다변량 정규분포는 선형변환에 대해 닫혀 있는(closed under linear transformation)분포입니다.
2. 조건부분포도 정규분포입니다.
다변량 정규분포 $\mathbf{X}=(\mathbf{X_1}, \, \mathbf{X_2})$에 대해 $\mathbf{X}_1 \mid \mathbf{X}_2 = \mathbf{x}_2$는 다변량 정규분포입니다. 조건부평균과 조건부공분산은 다음과 같이 계산됩니다.
\[
\mathbf{X}_1 \mid \mathbf{X}_2 = \mathbf{x}_2 \sim \mathcal{N}
\left(
\boldsymbol{\mu}_1 + \boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1} (\mathbf{x}_2 – \boldsymbol{\mu}_2),\
\boldsymbol{\Sigma}_{11} – \boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1} \boldsymbol{\Sigma}_{21}
\right)
\]
이 성질을 이용해서 ssGBLUP 모델을 구축할 수 있습니다.
3. 다변량 정규분포에서는 두 확률변수의 공분산이 0이면 두 확률변수가 서로 독립입니다.
다변량 정규분포에서는 선형독립과 확률독립이 같은 의미입니다. 이는 정규분포의 고유한 성질로 일반적인 분포에서는 일반적인 분포에서는 성립하지 않습니다.
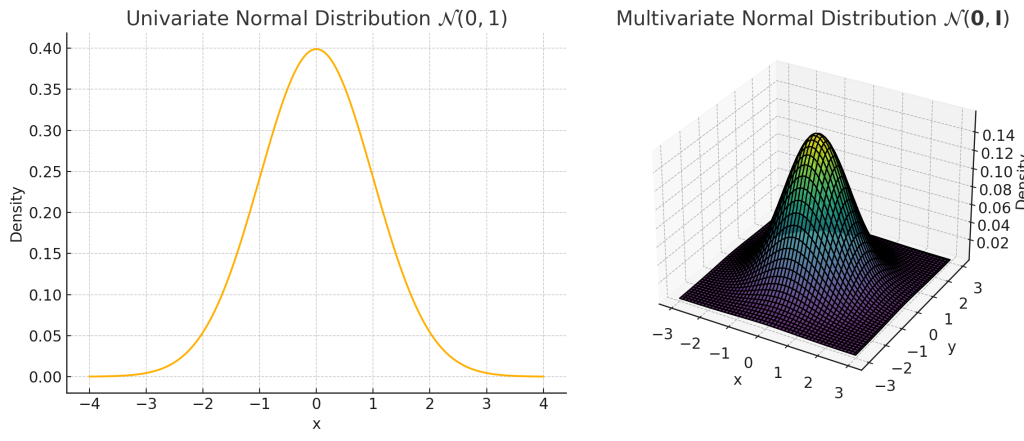
Fig. 1. 단변량 및 다변량 정규분포 시각화
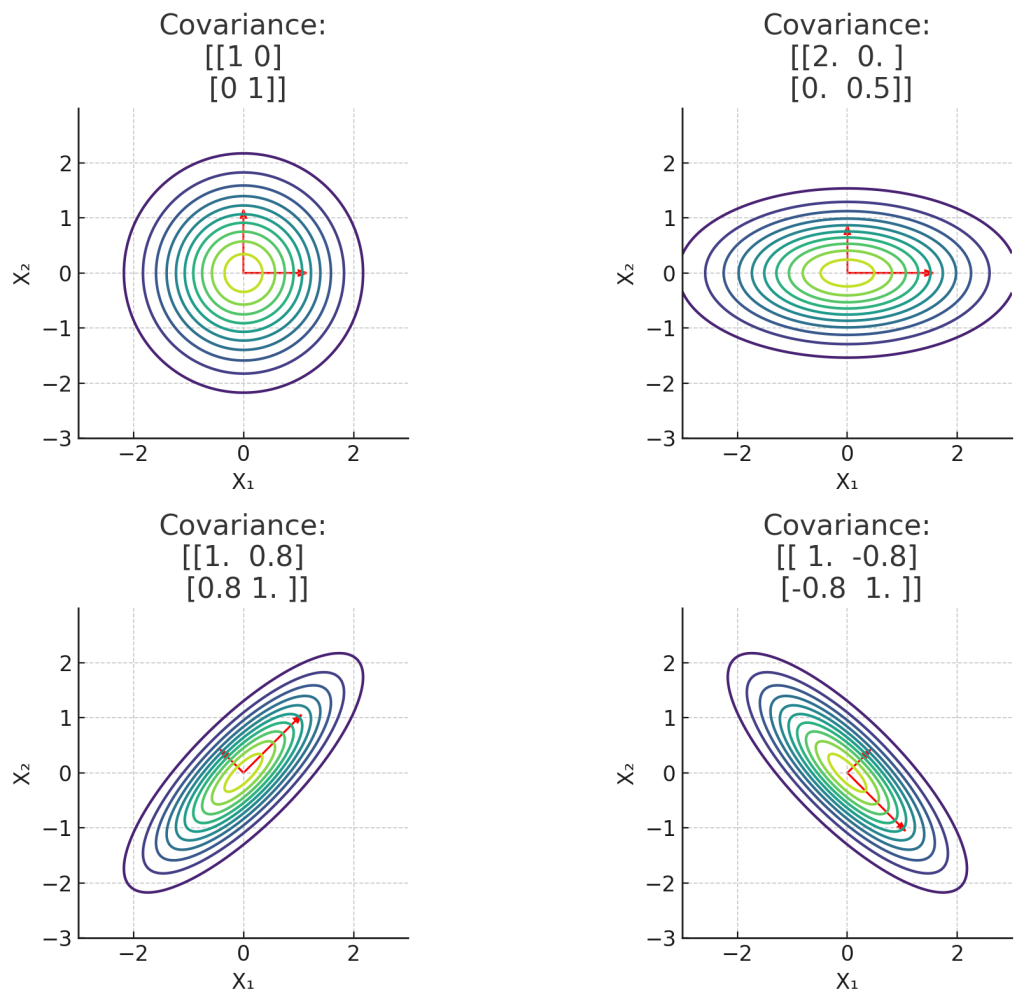
Fig. 2. 공분산행렬에 따른 2변량 정규분포의 확률밀도함수를 등고선과 고유벡터로 표현