DATA SCIENCE : 27
DATA SCIENCE eISSN
| 항목 | ANOVA | BLUE | PBLUP | GBLUP | ssGBLUP | deepGBLUP | 설명 |
|---|---|---|---|---|---|---|---|
| 모델식 | $y_{ij} = \mu + \alpha_i + \varepsilon_{ij}$ | $\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}$ | $\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$ | $\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$ | $\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$ | 입력은 비선형 함수 $f(\cdot)$ | ANOVA는 집단 간 평균 차이를 고정효과로 비교하는 모델 BLUE는 고정효과를 일반적인 선형모형 형태로 추정하는 모델 |
| 분포 가정 | $\varepsilon_{ij} \sim \mathcal{N}(0, \sigma^2)$ | $\boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}\sigma^2)$ | $\boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}\sigma_e^2)$ $\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{A}\sigma_u^2)$ | $\boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}\sigma_e^2)$ $\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{G}\sigma_u^2)$ | $\boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}\sigma_e^2)$ $\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{H}\sigma_u^2)$ | 정규성은 hidden layer에서 성립한다고 가정 가능 | $\boldsymbol{\varepsilon}$과 $\boldsymbol{u}$를 다변량 정규분포로 가정 ANOVA와 BLUE는 오차항만 고려, 나머지 모델들은 유전효과 추가 |
| $\mathbf{Z}\mathbf{u}$의 분포 | — | — | $\mathbf{Z}\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{ZAZ}^\top \sigma_u^2)$ | $\mathbf{Z}\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{ZGZ}^\top \sigma_u^2)$ | $\mathbf{Z}\mathbf{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{ZHZ}^\top \sigma_u^2)$ | 신경망의 hidden unit을 통해 표현됨 | 다변량 정규분포의 선형성으로 인해 $\mathbf{Z}\mathbf{u}$도 다변량 정규분포 ANOVA와 BLUE는 유전효과 미포함 |
| $\mathbf{y}$의 분포 | $y_{ij} \sim \mathcal{N}(\mu + \alpha_i, \sigma^2)$ | $\mathbf{y} \sim \mathcal{N}(\mathbf{X}\boldsymbol{\beta}, \mathbf{I} \sigma^2)$ | $\mathbf{y} \sim \mathcal{N}(\mathbf{X}\boldsymbol{\beta}, \mathbf{ZAZ}^\top \sigma_u^2 + \mathbf{I}\sigma_e^2)$ | $\mathbf{y} \sim \mathcal{N}(\mathbf{X}\boldsymbol{\beta}, \mathbf{ZGZ}^\top \sigma_u^2 + \mathbf{I}\sigma_e^2)$ | $\mathbf{y} \sim \mathcal{N}(\mathbf{X}\boldsymbol{\beta}, \mathbf{ZHZ}^\top \sigma_u^2 + \mathbf{I}\sigma_e^2)$ | $\mathbf{y} \sim \mathcal{N}(f(\cdot), \sigma_e^2)$ 또는 조건부 분포 | 다변량 정규분포의 선형성으로 인해 $\mathbf{y}$도 다변량 정규분포 모델이 복잡해질수록 $\mathbf{y}$의 분산 구조도 정교해짐 |
| 고정효과 | $\mu$, $\alpha_i$ | $\boldsymbol{\beta}$ | $\boldsymbol{\beta}$ | $\boldsymbol{\beta}$ | $\boldsymbol{\beta}$ | 포함 가능 (예: input layer), deepGBLUP은 X 입력을 통해 고정효과를 반영 가능 | ANOVA는 집단 평균 차이, 나머지는 행렬 $\mathbf{X}$ 사용 |
| 유전효과 | — | — | $\mathbf{u}$ | $\mathbf{u}$ | $\mathbf{u}$ | 암묵적 표현 (latent), 유전효과는 비선형 신경망에 내재됨 | ANOVA와 BLUE는 유전효과 없음 |
| 관계행렬 | — | — | $\mathbf{A}$ | $\mathbf{G}$ | $\mathbf{H}$ | $\mathbf{G}$ 또는 latent G, G 외에도 마커 직접 입력 가능 | 관계행렬은 유전효과가 있을 때만 등장 |
| 분산성분 | $\sigma^2$ | $\sigma^2$ | $\sigma_u^2$, $\sigma_e^2$ | $\sigma_u^2$, $\sigma_e^2$ | $\sigma_u^2$, $\sigma_e^2$ | $\sigma_e^2$ 또는 loss 기반 추정, loss나 dropout으로 오차 제어 | ANOVA와 BLUE는 단일 오차 분산만 추정 |
| $\operatorname{Var}(\boldsymbol{\varepsilon})$ | $\mathbf{I} \sigma^2$ | $\mathbf{I} \sigma^2$ | $\mathbf{I} \sigma_e^2$ | $\mathbf{I} \sigma_e^2$ | $\mathbf{I} \sigma_e^2$ | $\mathbf{I} \sigma_e^2$ 또는 미정, 오차항 분산은 추정 또는 implicit 처리 | 오차항은 모두 독립 등분산 가정 |
| $\operatorname{Var}(\mathbf{u})$ | — | — | $\mathbf{A} \sigma_u^2$ | $\mathbf{G} \sigma_u^2$ | $\mathbf{H} \sigma_u^2$ | 추정 안 됨 (암묵적 표현), 명시적 분산모델 없이 표현 | 유전효과가 포함된 모델만 분산 존재 |
| $\operatorname{Var}(\mathbf{y})$ | $\mathbf{I} \sigma^2$ | $\mathbf{I} \sigma^2$ | $\mathbf{ZAZ}^\top \sigma_u^2 + \mathbf{I} \sigma_e^2$ | $\mathbf{ZGZ}^\top \sigma_u^2 + \mathbf{I} \sigma_e^2$ | $\mathbf{ZHZ}^\top \sigma_u^2 + \mathbf{I} \sigma_e^2$ | 미정 (데이터 기반 추정), 분산은 모델 내 명시되지 않을 수 있음 | 유전효과와 오차효과가 합쳐진 전체 표현형 분산 |
Analysis of Variance
$$\mathbf{y}_{ij} = \mu + \alpha_i + \varepsilon_{ij},\quad \varepsilon_{ij} \sim \mathcal{N}(0, \sigma^2)$$
여기서, $\mathbf{y}_{ij}$는 $i$번째 처리(또는 집단)에서 $j$번째 관측값 (총 $n$개)
$\mu$는 전체 평균 (모든 집단의 공통 평균)
$\alpha_i$는 $i$번째 집단(처리)의 효과 (처리 간 차이)
$\varepsilon_{ij}$는 오차항(정규분포, 평균 0, 분산 $\sigma^2$)
$$\mathbf{y} \sim \mathcal{N}(\mu \cdot \mathbf{1}_n + \boldsymbol{\alpha},\; \sigma^2 \mathbf{I})$$
여기서, $\mathbf{y}$는 관측값 전체 벡터 ($n\times1$)
$\mu \cdot \mathbf{1}_n$은 전체평균을 모든 관측값에 적용한 벡터
$\boldsymbol{\alpha}$는 처리 집단에 해당하는 효과 벡터 (예: 더미코딩 형태)
$\sigma^2 \mathbf{I}$는 등분산 정규오차 가정
추정하고자 하는 것: 모수
| 모수 기호 | 모수 설명 |
|---|---|
| $\mu$ | 전체 평균 |
| $\alpha_i$ | 각 처리의 효과 |
| $\sigma^2$ | 오차의 분산 |
모수를 추정한 결과식: 추정량
| 추정량 기호 | 추정량 | 추정량 설명 |
|---|---|---|
| $\hat{\mu}$ | $$\hat{\mu} = \frac{1}{N} \sum_{i=1}^{a} \sum_{j=1}^{n_i} y_{ij}$$ | 표본전체평균 |
| $\hat{\alpha}_i$ | $$\hat{\alpha}_i =\frac{1}{n_i} \sum_{j=1}^{n_i} y_{ij} – \frac{1}{N} \sum_{i=1}^{a} \sum_{j=1}^{n_i} y_{ij}$$ | 표본의 각 집단평균-표본전체평균 |
| $\hat{\sigma}^2$ | $$\hat{\sigma}^2 = \frac{\sum\limits_{i=1}^{a} \sum_{j=1}^{n_i} (y_{ij} – \hat{y}_{ij})^2}{N – a} = \frac{SS_E}{N – a}$$ | 잔차제곱합/자유도 |
최소제곱법(OLS, Ordinary Least Squares)으로 추정량 유도
잔차제곱합($SS_E$)을 최소로 하는 $\hat{\mu}$, $\hat{\alpha_i}$ 찾기.
$$SS_E = \sum_{i=1}^{a} \sum_{j=1}^{n_i} \left( y_{ij} – \hat{\mu} – \hat{\alpha}_i \right)^2$$
단. 고유한 해를 갖기 위한 제약조건
$$\sum_{i=1}^{a} \hat{\alpha_i}= 0$$
여기서 $a$는 집단수
다음의 제약조건을 포함한 라그랑주안 함수를 편미분하여 최소제곱 추정량 ($\hat{\mu}$, $\hat{\alpha_i}$)을 유도
$$\mathcal{L}(\mu, \alpha_1, \dots, \alpha_a, \lambda)= \sum_{i=1}^{a} \sum_{j=1}^{n_i} (y_{ij} – \mu – \alpha_i)^2+ \lambda \left( \sum_{i=1}^{a} \alpha_i \right)$$
최종해인 추정량을 구하면
$$\hat{\mu} = \frac{1}{N} \sum_{i=1}^{a} \sum_{j=1}^{n_i} y_{ij}$$
$$\hat{\alpha}_i =\frac{1}{n_i} \sum_{j=1}^{n_i} y_{ij} – \frac{1}{N} \sum_{i=1}^{a} \sum_{j=1}^{n_i} y_{ij}$$
$$\hat{\sigma}^2 = \frac{\sum_{i=1}^{a} \sum_{j=1}^{n_i} (y_{ij} – \hat{y}_{ij})^2}{N – a} = \frac{\text{SSE}}{N – a}$$
유의성 검정
귀무가설
$$H_0: \alpha_1 = \alpha_2 = \cdots = \alpha_a = 0$$
대립가설
$$H_1: \text{적어도 하나의 } \alpha_i \ne 0$$
F통계량
$$F = \frac{MS_B}{MS_E} = \frac{SS_B / (a – 1)}{SS_E / (N – a)}$$
Fisher (1925), 유전학자, 통계학의 시조
처리 효과와 오차 분해. 선형모형의 출발점
시험육종, 품종비교실험
실험설계, 생물학, 약리학
Best Linear Unbiased Estimator
$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}$$
$$\mathbf{y} \sim \mathcal{N}(X\boldsymbol{\beta},\; \sigma^2 \mathbf{I})$$
여기서, $\mathbf{y} \in \mathbb{R}^{n \times 1}$는 관측값 벡터 (표현형 또는 종속변수)
$\mathbf{X} \in \mathbb{R}^{n \times p}$는 디자인 행렬 (독립변수, 설명변수)
$\boldsymbol{\beta} \in \mathbb{R}^{p \times 1}$는 고정효과 계수 벡터
$\sigma^2 \mathbf{I}$는 등분산 가정 하의 오차 공분산 행렬
$\mathcal{N}(\cdot,\cdot)$는 다변량 정규분포
| 용어 | 설명 | 의미 |
|---|---|---|
| Best | 최선의 (최소 분산) | 동일한 조건의 다른 추정량보다 분산이 가장 작다 |
| Linear | 선형 | 추정량 $\hat{\boldsymbol{\beta}}$은 관측값 $\mathbf{y}$의 선형결합으로 표현된다. $\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$ 여기서, $\mathbf{X}$은 입력데이터로 상수이므로 $(\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top$도 고정행렬(비확률적 상수) |
| Unbiased | 불편 | 기대값이 진짜 모수와 같다: $\mathbb{E}[\hat{\boldsymbol{\beta}}] = \boldsymbol{\beta}$ |
| Estimator | 추정량 | 모수를 추정하는 식, 보통 표본에서 계산됨 |
추정하고자 하는 것과 추정결과
| 추정대상 기호 | 추정대상 | 추정량 | 비고 |
|---|---|---|---|
| $\boldsymbol{\beta}$ | 회귀계수 벡터 | $\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$ | $p$는 계수의 수: 설계행렬 $\mathbf{X}$의 열 수 |
| $\sigma^2$ | 오차 분산 | $\hat{\sigma}^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$ | $n$은 전체 관측값 개수 $p$는 집단수 $\mathbf{e}= \mathbf{y} – \mathbf{X}\boldsymbol{\beta}$ |
$\boldsymbol{\beta}$의 추정방법: 최소제곱법(OLS)
잔차제곱합($SS_{Res}$)을 최소화하는 $\boldsymbol{\beta}$ 구하기
$$SS_{Res}=\sum_{i=1}^{n} (y_i – \hat{y}_i)^2 = (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})^\top (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})=\mathbf{e}^\top \mathbf{e}$$
미분하여 최소값 조건을 구하면
$$\hat{\boldsymbol{\beta}}_{\text{OLS}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$$
조건은 $\mathbf{X}^\top \mathbf{X}$ 가 가역(invertible)해야 함
오차항이 정규분포가 아니더라도 모델이 선형성 ($\boldsymbol{X}\beta$가 상수)이 있고 오차의 기대값이 0이고 분산이 등분산이고 독립성이 있으면 최소제곱추정량은 모든 선형불편추정량 중에서 분산이 가장 작은 최적추정량 BLUE(Best Linear Unbiased Estimator)임. 이를 Gauss-Markov 정리라고 함.
$\boldsymbol{\beta}$의 추정방법: 최대우도추정(MLE)
정규성을 가정하면 확률밀도함수
$$f(\mathbf{y} \mid \boldsymbol{\beta}, \sigma^2)
= \frac{1}{(2\pi\sigma^2)^{n/2}} \exp\left( -\frac{1}{2\sigma^2} (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})^\top (\mathbf{y} – \mathbf{X}\boldsymbol{\beta}) \right)$$
로그우도함수
$$\log L(\boldsymbol{\beta}, \sigma^2 \mid \mathbf{y})
= -\frac{n}{2} \log(2\pi\sigma^2)
– \frac{1}{2\sigma^2} (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})^\top (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})$$
MLE(최대우도추정)하면
$$\hat{\boldsymbol{\beta}}_{\text{MLE}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$$
| 오차항 조건 | 회귀계수 벡터 $\boldsymbol{\beta}$의 추정량 | 성질 |
|---|---|---|
| 정규성 없음 | $\hat{\boldsymbol{\beta}}_{\text{OLS}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$ | 오차항이 정규분포를 따르지 않아도, Gauss–Markov 조건만 만족하면 OLS로 추정한 $\hat{\boldsymbol{\beta}}_{\text{OLS}}$는 최선선형불편추정량 (BLUE, Best Linear Unbiased Estimaor)임 |
| 정규성 있음 | $\hat{\boldsymbol{\beta}}_{\text{MLE}}=(\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$ $\hat{\boldsymbol{\beta}}_{\text{MLE}}=\hat{\boldsymbol{\beta}}_{\text{OLS}}$ | 오차항을 등분산가정 다변량 정규분포로 가정 $$\boldsymbol{\varepsilon} \sim \mathcal{N}(0, \sigma^2 \mathbf{I})$$ 선형변환에 따라 다음의 선형모델도 정규분포 $$\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}$$ 여기서, $\mathbf{X} \boldsymbol{\beta}$는 상수항 따라서 반응변수벡터 $\boldsymbol{y}$는 다변량 정규분포 $$\mathbf{y} \sim \mathcal{N}(\mathbf{X} \boldsymbol{\beta}, \sigma^2 \mathbf{I})$$ $\mathbf{y}$의 확률밀도함수 $f(\boldsymbol{y}|\boldsymbol{\beta},\sigma^2)$이 존재하고 로그우드함수 $\log L(\boldsymbol{\beta}, \sigma^2 \mid \mathbf{y})$를 정의할 수 있음. 따라서 최대우도추정량(MLE)를 구할 수 있고 OLE로 구한 추정량과 같음, 그리고 두 추정량은 모두 BLUE임 |
$\sigma^2$의 추정방법: 불편추정량(Unbiased Estimator, 자유도반영)
오차분산의 추정값
$$\hat{\sigma}^2 = \frac{\mathbf{e}^\top \mathbf{e}}{n – p}$$
여기서, $y_i$는 관측값
$\hat{y}_i$는 예측값
$\mathbf{e} = \mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}}$는 잔차벡터
$\mathbf{e}^\top \mathbf{e}$는 잔차제곱합의 벡터 표현
$n$은 관측값 개수
$p$는 추정된 계수의 수 (설계행렬 $\boldsymbol{X}$의 열 수)
| 추정 대상 | 추정 방법 | 수식 |
|---|---|---|
| $\boldsymbol{\beta}$ | 최소제곱법 (잔차제곱합 최소화) MLE | $\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$ |
| $\sigma^2$ | 잔차 제곱합을 자유도로 나눈 값 | $\hat{\sigma}^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$
여기서, $n$은 표본크기 $p$는 표본내집단수 |
$$\boldsymbol{\alpha} =
\begin{bmatrix}
\alpha_{D1} \\
\alpha_{D2}
\end{bmatrix}$$
$\boldsymbol{\beta}$
$$\boldsymbol{\beta} =
\begin{bmatrix}
\mu \\
\alpha_{D1} \\
\alpha_{D2} \\
\beta_{\text{도체중}}
\end{bmatrix}
=
\begin{bmatrix}
\beta_0 \\
\beta_{D1} \\
\beta_{D2} \\
\beta_{\text{도체중}}
\end{bmatrix}$$
Aitken (1935), 수리통계학자
고정효과의 최적 선형 추정량
형질간 회귀 분석
경제학, 회귀분석, 기업 성과 예측
Pedigree-Based Best Linear Unbiased Prediction
$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$$
$$\mathbf{y} \sim \mathcal{N}(X\boldsymbol{\beta},\; ZAZ^\top \sigma_u^2 + I\sigma_e^2)$$
여기서, $\mathbf{y} \in \mathbb{R}^{n \times 1}$는 표현형(관측값) 벡터
$\mathbf{X} \in \mathbb{R}^{n \times p}$는 고정효과 디자인 행렬
$\boldsymbol{\beta} \in \mathbb{R}^{p \times 1}$는 고정효과 계수
$\mathbf{Z} \in \mathbb{R}^{n \times q}$는 개체의 유전효과 할당 행렬 (통상 단위행렬 비슷한 형태)
$\mathbf{A} \in \mathbb{R}^{q \times q}$는 혈연관계행렬 (pedigree relationship matrix)
$\sigma^2_u$는 유전(우성) 효과의 분산
$\sigma^2_e$는 환경 오차의 분산
$\mathbf{I}$는 항등행렬 (단순한 오차 구조)
| 용어 | 설명 | 의미 |
|---|---|---|
| Pedigree-based | 계통도 기반 | 예측 시 개체 간 유전적 유사도는 계보 정보를 기반으로 한 관계행렬 A를 사용함 |
| Best | 최선의 (최소 분산) | 동일한 조건의 다른 예측량보다 분산이 가장 작다 |
| Linear | 선형 | 예측량 $\hat{u}$는 관측값 $\mathbf{y}$의 선형결합으로 표현된다. $$ |
| Unbiased | 불편 | 기댓값이 진짜 육종가와 같다 $\mathbb{E}[\hat{u}] = u$ |
| Prediction | 예측량 | 계통도 정보를 바탕으로 개체의 유전적 가치를 예측한 값 |
추정하고자 하는 것과 추정결과
| 기호 | 추정대상 | 추정량 |
|---|---|---|
| $\beta$ | 고정효과 회귀계수 | $\hat{\beta} = (\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$ |
| $u$ | 개체의 육종가 | $\hat{u} = \mathbf{G} \mathbf{Z}^\top \mathbf{V}^{-1} (\mathbf{y} – \mathbf{X} \hat{\beta})$, 단 $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$ |
| $\sigma_u^2$ | 육종가 분산성분 | REML로 추정: 유사도 기반 반복 알고리즘 사용 |
| $\sigma_e^2$ | 오차 분산성분 | REML 또는 $\hat{\sigma}_e^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$ (단순 선형 모형 시) |
모델 설정
$$\mathbf{y} \sim N(\mathbf{X} \boldsymbol{\beta}, \mathbf{V})$$
여기서, $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$
목적함수는 최소제곱법(선형추정량의 평균제곱 오차 최소화)
$$Q(\beta, u) = (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u)^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u) + u^\top \mathbf{G}^{-1} u$$
여기서, $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$
$Q(\beta, u)$의 앞쪽 항은 오차항의 가중제곱합, 뒤쪽 항은 확률효과의 정규분포 페널티입니다.
이 목적함수를 미분하여 MME를 유도
MME(혼합모델방정식, Mixed Model Equation)는 고정효과와 확률효과를 동시에 추정하기 위한 시스템
선형 모델과 정규분포 가정, 선형 최소제곱 또는 우도 최적화로부터 유도됨
목적함수를 편미분하여 0으로 설정
$\beta$로 편미분
$$-2 \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u) = 0\Rightarrow$$
$$\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \beta + \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} u
= \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$$
$u$로 편미분
$$-2 \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u)
+ 2 \mathbf{G}^{-1} u = 0\Rightarrow$$
$$\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} \beta
+ (\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1}) u
= \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}$$
편미분한 두 식을 행렬로 정리 -> MME 도출
MMEMME(혼합모델방정식, Mixed Model Equation)는 다음식으로 표현됨
$$
\begin{bmatrix}
\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} & \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} \\
\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} & \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1}
\end{bmatrix}
\begin{bmatrix}
\hat{\boldsymbol{\beta}} \\
\hat{\mathbf{u}}
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y} \\
\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}
\end{bmatrix}
$$
여기서, $\mathbf{G}$는 $\sigma_u^2 \mathbf{A}$
고정효과 방정식
$$\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \hat{\boldsymbol{\beta}} + \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} \hat{\mathbf{u}} = \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$$
고정효과 방정식에서 $\hat{\beta}$로 정리
$$\hat{\boldsymbol{\beta}} = \left( \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \right)^{-1} \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{Z} \hat{\mathbf{u}})$$
윗식은 고정효과 $\beta$의 추정량을 확률효과 $\hat{u}$를 알고 있을 때의 조건부 형태로 나타낸 것
확률효과 방정식
$$\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} \hat{\boldsymbol{\beta}} + \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right) \hat{\mathbf{u}} = \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}$$
$\hat{u}$식에 $\hat{\beta}$가 포함된 형태로 육종가를 정리
$$\left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right) \hat{\mathbf{u}} = \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$$
양변에 $\left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1}$를 곱하면$$\hat{\mathbf{u}} = \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1} \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$$
육종가 $\hat{\mathbf{u}}$의 추정량은 BLUP이며 혼합모형방정식(MME)의 두 번째 행을 역행렬로 정리한 결과
MME에서 위의 두식처럼 불록행렬을 만들고 이를 이용하여 두 추정량을 계산하는 데 이 두 식은 서로 의존하므로 반복계산 또는 동시 해법을 사용
또는 MME에서 역행렬을 이용해서 두 추정량을 계산하는 데 선형시스템해법(예, LU분해, Cholesky분해 등)을 사용함
실전에서는 R, Python 등 에서 내부적으로 MME를 구성해 수치적으로 해를 구함
REML (Restricted Maximum Likelihood) 추정 과정
PBLUP에서의 분산행렬($\mathbf{G}$, $\mathbf{R}$)과 분산성분($\sigma_u^2$, $\sigma_e^2$)
$$\mathbf{G} = \sigma_u^2 \mathbf{A}, \quad \mathbf{R} = \sigma_e^2 \mathbf{I}$$
분산성분, 회귀계수벡터, 육종가벡터를 REML으로 추정하는 단계적 과정
분산성분 수렴기준(convergence criterion)
| 알고리즘 | 수렴 기준 | 일반 값 |
|---|---|---|
| EM-REML | 절대 변화량 or 상대 변화량 | $10^{-6}$ |
| AI-REML | 로그우도 변화 or 분산성분 상대오차 | $10^{-8}$ |
| 소프트웨어 | asreml, sommer, lme4, blupf90 등 | 기본값 또는 설정 가능 |
추정 요약
PBLUP은 MME를 통해 고정효과와 확률효과를 동시에 추정
분산성분은 REML 등으로 추정
| 추정 대상 | 추정 방법 | 수식 |
|---|---|---|
| $\boldsymbol{\beta}$ | 혼합모형방정식(MME) 이용한 고정효과 추정 | $\hat{\boldsymbol{\beta}} = \left( \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \right)^{-1} \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{Z} \hat{\mathbf{u}})$ |
| $\mathbf{u}$ | 혼합모형방정식(MME) 이용한 BLUP (확률효과) | $\hat{\mathbf{u}} = \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1} \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$ 단, $\mathbf{G} = \sigma_u^2 \mathbf{A}$ |
| $\sigma_e^2$ | REML 또는 잔차제곱합 기반 추정 | $\hat{\sigma}_e^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$ 여기서, $n$은 관측값 개수, $p$는 고정효과의 수 |
| $\sigma_u^2$ | REML로 분산성분 추정 | 최대우도 기반 반복 알고리즘 (예: EM-REML) |
모델 평가
| 평가 방법 | 내용 |
|---|---|
| 상관계수 | $\mathrm{cor}(\hat{u}, y) / \sqrt{h^2}$ |
| MSE | $\frac{1}{n} \sum (y_i – \hat{y}_i)^2$ |
| LRT | $\sigma_u^2$ 유의성 검정 |
| AIC/BIC | 모형 비교용 |
| Cross-validation | 외부 데이터로 검증 정확도 평가 |
Henderson (1975), 유전육종학자
혈통 기반 유전효과 예측
잠재적유전능력(육종가)에 기반한 육종
가축·작물 육종, 개량
계층형 조직 분석, 인사 평가, 기업가치 요소 추정
Genomic Best Linear Unbiased Prediction
$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$$
$$\mathbf{y} \sim \mathcal{N}(X\boldsymbol{\beta},\; ZGZ^\top \sigma_u^2 + I\sigma_e^2)$$
여기서, $\mathbf{y} \in \mathbb{R}^{n \times 1}$는 표현형(관측값) 벡터 (예: 도체중, 근내지방도 등)
$\mathbf{X} \in \mathbb{R}^{n \times p}$는 고정효과 디자인 행렬 (예: 성별, 연도)
$\boldsymbol{\beta} \in \mathbb{R}^{p \times 1}$는 고정효과 계수
$\mathbf{Z} \in \mathbb{R}^{n \times q}$는 개체-유전효과 매핑 행렬 (보통 단위 행렬)
$\mathbf{A} \in \mathbb{R}^{q \times q}$는 유전체 유사도행렬 (Genomic relationship matrix)
$\sigma^2_u$는 유전효과의 분산 (random effect variance)
$\sigma^2_e$는 환경 오차의 분산
$\mathbf{I}$는 단위행렬 (오차 간 독립성 가정)
| 용어 | 설명 | 의미 |
|---|---|---|
| Genomic-based | 유전체 기반 | 예측 시 유전자의 마커 정보를 이용하며, 개체 간 유전적 유사도는 유전체 정보를 기반으로 한 관계행렬 $\boldsymbol{G}$를 사용함 |
| Best | 최선의 (최소 분산) | 동일한 조건의 다른 예측량보다 분산이 가장 작다 |
| Linear | 선형 | 예측량 $\hat{\boldsymbol{g}}$는 관측값 $\boldsymbol{y}$의 선형결합으로 표현된다. $$ |
| Unbiased | 불편 | 기대값이 진짜 육종가와 같다 $\mathbb{E}[\hat{g}] = g$ |
| Prediction | 예측량 | 유전체 정보를 바탕으로 개체의 유전적 가치를 예측한 값 |
| 기호 | 추정대상 | 추정결과(추정량) |
|---|---|---|
| $\beta$ | 고정효과 회귀계수 | $\hat{\beta} = (\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$ |
| $u$ | 개체의 육종가 (확률효과) | $\hat{u} = \mathbf{G} \mathbf{Z}^\top \mathbf{V}^{-1} (\mathbf{y} – \mathbf{X} \hat{\beta})$, 단 $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$ |
| $\sigma_u^2$ | 육종가 분산 | REML로 추정: 유사도 기반 반복 알고리즘 사용 |
| $\sigma_e^2$ | 오차 분산 | REML 또는 $\hat{\sigma}_e^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$ (단순 선형 모형 시) |
모델 설정
$$\mathbf{y} \sim N(\mathbf{X} \boldsymbol{\beta}, \mathbf{V})$$
여기서, $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$
목적함수는 최소제곱법(선형추정량의 평균제곱 오차 최소화)
$$Q(\beta, u) = (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u)^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u) + u^\top \mathbf{G}^{-1} u$$
여기서, $\mathbf{V} = \mathbf{Z} \mathbf{G} \mathbf{Z}^\top + \mathbf{R}$
$Q(\beta, u)$의 앞쪽 항은 오차항의 가중제곱합, 뒤쪽 항은 확률효과의 정규분포 페널티입니다.
이 목적함수를 미분하여 MME를 유도
MME는 고정효과와 확률효과를 동시에 추정하기 위한 시스템
선형 모델과 정규분포 가정, 선형 최소제곱 또는 우도 최적화로부터 유도됨
목적함수를 편미분하여 0으로 설정
$\beta$로 편미분
$$-2 \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u) = 0\Rightarrow$$
$$\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \beta + \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} u
= \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$$
$u$로 편미분
$$-2 \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \beta – \mathbf{Z} u)
+ 2 \mathbf{G}^{-1} u = 0\Rightarrow$$
$$\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} \beta
+ (\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1}) u
= \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}$$
편미분한 두 식을 행렬로 정리 -> MME 도출
MME는 다음식으로 표현됨
$$
\begin{bmatrix}
\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} & \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} \\
\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} & \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1}
\end{bmatrix}
\begin{bmatrix}
\hat{\boldsymbol{\beta}} \\
\hat{\mathbf{u}}
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y} \\
\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}
\end{bmatrix}
$$
여기서, $\mathbf{G}$는 $\sigma_u^2 \mathbf{A}$
고정효과 방정식
$$\mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \hat{\boldsymbol{\beta}} + \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{Z} \hat{\mathbf{u}} = \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{y}$$
고정효과 방정식에서 $\hat{\beta}$로 정리
$$\hat{\boldsymbol{\beta}} = \left( \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \right)^{-1} \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{Z} \hat{\mathbf{u}})$$
윗식은 고정효과 $\beta$의 추정량을 확률효과 $\hat{u}$를 알고 있을 때의 조건부 형태로 나타낸 것
육종가 방정식
$$\mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{X} \hat{\boldsymbol{\beta}} + \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right) \hat{\mathbf{u}} = \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{y}$$
$\hat{u}$식에 $\hat{\beta}$가 포함된 형태로 육종가 방정식을 정리
$$\left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right) \hat{\mathbf{u}} = \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$$
양변에 $\left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1}$를 곱하면$$\hat{\mathbf{u}} = \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1} \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$$
이 수식은 육종가 $\hat{\mathbf{u}}$의 BLUP 추정식이며 혼합모형방정식(MME)의 두 번째 행을 역행렬로 정리한 결과
MME에서 위의 두식처럼 불록행렬을 만들고 이를 이용하여 두 추정량을 계산하는 데 이 두 식은 서로 의존하므로 반복계산 또는 동시 해법을 사용
또는 MME에서 역행렬을 이용해서 두 추정량을 계산하는 데 선형시스템해법(예, LU분해, Cholesky분해 등)을 사용함
실전에서는 R, Python 등 에서 내부적으로 MME를 구성해 수치적으로 해를 구함
REML (Restricted Maximum Likelihood) 추정 과정
GBLUP에서의 분산행렬($\mathbf{G}$, $\mathbf{R}$)과 분산성분($\sigma_g^2$, $\sigma_e^2$)
$$\mathbf{G} = \sigma_g^2 \mathbf{G}, \quad \mathbf{R} = \sigma_e^2 \mathbf{I}$$
분산성분, 회귀계수벡터, 육종가벡터를 REML으로 추정하는 단계적 과정
분산성분 수렴기준(convergence criterion)
| 알고리즘 | 수렴 기준 | 일반 값 |
|---|---|---|
| EM-REML | 절대 변화량 or 상대 변화량 | $10^{-6}$ |
| AI-REML | 로그우도 변화 or 분산성분 상대오차 | $10^{-8}$ |
| 소프트웨어 | asreml, sommer, lme4, blupf90 등 | 기본값 또는 설정 가능 |
추정 요약
PBLUP은 MME를 통해 고정효과와 확률효과를 동시에 추정
분산성분은 REML 등으로 추정
| 추정 대상 | 추정 방법 | 수식 |
|---|---|---|
| $\boldsymbol{\beta}$ | 혼합모형방정식(MME) 이용한 고정효과 추정 | $\hat{\boldsymbol{\beta}} = \left( \mathbf{X}^\top \mathbf{R}^{-1} \mathbf{X} \right)^{-1} \mathbf{X}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{Z} \hat{\mathbf{u}})$ |
| $\mathbf{u}$ | 혼합모형방정식(MME) 이용한 BLUP (확률효과) | $\hat{\mathbf{u}} = \left( \mathbf{Z}^\top \mathbf{R}^{-1} \mathbf{Z} + \mathbf{G}^{-1} \right)^{-1} \mathbf{Z}^\top \mathbf{R}^{-1} (\mathbf{y} – \mathbf{X} \hat{\boldsymbol{\beta}})$ 단, $\mathbf{G} = \sigma_u^2 \mathbf{A}$ |
| $\sigma_e^2$ | REML 또는 잔차제곱합 기반 추정 | $\hat{\sigma}_e^2 = \dfrac{\mathbf{e}^\top \mathbf{e}}{n – p}$ 여기서, $n$은 관측값 개수, $p$는 고정효과의 수 |
| $\sigma_u^2$ | REML로 분산성분 추정 | 최대우도 기반 반복 알고리즘 (예: EM-REML) |
모델 평가
| 평가 방법 | 내용 |
|---|---|
| 상관계수 | $\mathrm{cor}(\hat{u}, y) / \sqrt{h^2}$ |
| MSE | $\frac{1}{n} \sum (y_i – \hat{y}_i)^2$ |
| LRT | $\sigma_u^2$ 유의성 검정 |
| AIC/BIC | 모형 비교용 |
| Cross-validation | 외부 데이터로 검증 정확도 평가 |
VanRaden (2008), 유전육종학자
유전체 기반 유전효과 예측
잠재적유전능력(육종가)에 기반한 육종
유전체육종, 유전평가
고객 행동 기반 주가 반응 예측, 마케팅 ROI 분석
Single-Step Genomic Best Linear Unbiased Prediction
$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon}$$
$$\mathbf{y} \sim \mathcal{N}(X\boldsymbol{\beta},\; ZHZ^\top \sigma_u^2 + I\sigma_e^2)$$
여기서, $\mathbf{y} \in \mathbb{R}^{n \times 1}$는 표현형(관측값) 벡터 (예: 근내지방도, 도체중 등)
$\mathbf{X} \in \mathbb{R}^{n \times p}$는 고정효과 디자인 행렬 (예: 성별, 연도, 지역 등)
$\boldsymbol{\beta} \in \mathbb{R}^{p \times 1}$는 고정효과 계수
$\mathbf{Z} \in \mathbb{R}^{n \times q}$는 개체별 유전효과를 연결하는 매핑 행렬
$\mathbf{H} \in \mathbb{R}^{q \times q}$는 혈통행렬 $\boldsymbol{A}$과 유전체행렬
$\boldsymbol{G}$을 통합한 혼합 유전관계행렬
$\sigma^2_u$는 유전효과의 분산 (random effect variance)
$\sigma^2_e$는 오차항 분산 (환경효과 포함)
$\mathbf{I}$는 단위행렬 (오차 간 독립성 가정)
$$H^{-1} = A^{-1} +
\begin{bmatrix}
0 & 0 \\
0 & G^{-1} – A_{22}^{-1}
\end{bmatrix}$$
여기서, $A^{-1}$는 전체 개체의 혈통기반 관계 역행렬
$G^{-1}$는 유전체 정보가 있는 개체의 유전체 관계 역행렬
$A_{22}^{-1}$는 그 유전체 개체들의 혈통기반 하위행렬 역행렬
Aguilar, Misztal et al. (2010) 유전육종학자들
혈통+유전체 통합 기반 유전효과 예측
잠재적유전능력(육종가)에 기반한 육종
국가 단위 개체평가, 실무육종
불완전 정보 보정, 부분 정보 기반 주가 산정, 복합 HR/재무 통합 분석
deeplearning Genomic Best Linear Unbiased Prediction
$$\hat{y} = \bar{y}_{\text{train}} + \hat{b}_{\text{deep}} + \hat{b}_a + \hat{b}_d + \hat{b}_e$$
여기서, $ \bar{y}_{\text{train}}$는 훈련 데이터의 평균
$\hat{b}_{\text{deep}}$ deep learning 모듈이 추정한 유전효과
$\hat{b}_a$는 additive (가법) 유전효과
$\hat{b}_d$는 dominance (우성) 유전효과
$\hat{b}_e$는 epistasis (상호작용) 유전효과
고정효과
$$\boldsymbol{\beta}$$
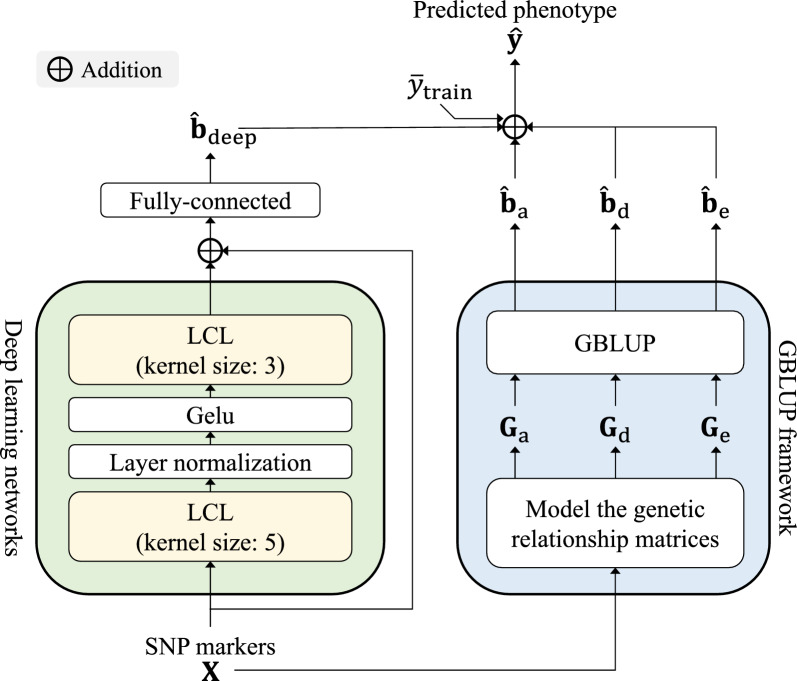
확률효과 (유전체 위치효과를 딥러닝으로 반영)
$$\boldsymbol{u_{deep}}$$
$$\boldsymbol{u_{g}}$$
Lee et al. (2023) 유전육종학자들
딥러닝의 유전체의 위치에 따른 특성 추출 능력과 GBLUP의 유전행렬 기반 예측력을 통합하여 표현형 예측 성능을 향상시킨 모델.
잠재적유전능력(육종가)에 기반한 육종
LCL 기반 딥러닝 모듈이 SNP의 위치 정보를 활용
전통 GBLUP + deep feature 병렬 조합으로 예측 정확도 향상
정규분포 기반 해석과 딥러닝의 표현력을 모두 고려한 최신 예측틀
복합 HR·재무 통합 분석, 부분 정보 기반 주가 산정
유전체 기반 개체 선발, 딥러닝 기반 표현형 보완 예측
