다변량 정규분포(multivariate normal distribution)입니다.
변량은 확률변수의 실제 관측값을 의미합니다.
어떤 확률공간 $(\Omega, \mathcal{F}, P)$ 위에 정의된 정규분포 확률변수 벡터 $ \mathbf{X} = (X_1, \ldots, X_n)^\top $가 있을 때,
그 벡터가 표현공간 $ \mathbb{R}^n $에서 따르는 결합확률분포 $ P_{\mathbf{X}} $는 다변량 정규분포 $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$입니다.
확률변수는 항상 어떤 확률공간 ($\Omega$, $\mathcal{F}$, $P$) 상에 정의됩니다.
정규분포를 나타내는 확률변수의 벡터는 벡터형 확률변수라고 할 수 있으며 다음과 같이 표현됩니다.
$$X_i \sim \mathcal{N}(\mu_i, \sigma_i^2) \rightarrow \mathbf{X}=(X_1, \ldots, X_n)^\top \rightarrow \mathbf{X} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$$
표현공간(codomain, value space)은 확률변수 벡터의 값이 이루는 공간입니다. 이는 결합확률분포가 정의되는 공간($\mathbb{R}$, $\mathcal{B}(\mathbb{R}^n)$)이기도 합니다.
$\mathcal{B}(\mathbb{R}^n)$은 $\mathbb{R}^n$위의 Borel $\sigma$-대수 (Borel σ-algebra)이 $\mathbb{R}^n$에서 확률분포가 정의되는 사건공간(event space)입니다.
표현공간(codomain)은 확률변수 또는 확률변수 벡터가 나타나는 공간입니다. 이 공간 위에서 확률분포나 결합확률분포가 정의됩니다.
확률변수 $X$ 또는 확률변수 벡터 $\mathbf{X}$의 표현공간은 다음과 같이 수학적으로 나타냅니다.
단일 확률변수 $X$의 경우
$$X : \Omega \to \mathbb{R}$$
여기서, $\mathbb{R}$은 표현공간
확률변수 벡터 $\mathbf{X} = (X_1, \ldots, X_n)^\top$의 경우
$$\mathbf{X} : \Omega \to \mathbb{R}^n$$
여기서, $\mathbb{R}^n$는 표현공간
$n$은 벡터의 원소 개수이며 벡터의 차원
Table 1. 확률공간 관련 용어의 표기 및 정의
| 용어 | 표기 | 정의 | 설명 |
|---|---|---|---|
| 확률공간 (probability space) | $(\Omega, \mathcal{F}, P)$ | 표본공간, 사건공간, 확률측도로 구성된 삼중 구조 | 확률론의 기본 틀 |
| 표본공간 (sample space) | $\Omega$ | 확률변수가 정의되는 공간 | 실험의 가능한 모든 결과들의 집합 표본공간의 원소는 더이 상 나눌 수 없는 기저사건(elementary event, 단일사건, 기초사건, 원자사건)의 결과 표본공간은 기저사건의 공 표본공간의 원소인 기저사건들의 확률의 합은 1 표본공간은 “기저사건들의 공간”이지, 통계적 의미의 “표본 데이터의 공간”이 아. |
| 사건공간 (event space) | $\mathcal{F}$ | 확률이 정의되는 집합들의 σ-대수 | $\Omega$의 부분집합 중 확률을 부여할 수 있는 집합들의 모임 사건들의 공간 |
| 확률측도 (probability measure) | $P$ | 사건공간의 각 사건에 확률을 부여하는 함수 | $P: \mathcal{F} \to [0,1]$ |
| 표현공간 (codomain) | $\mathbb{R}$, $\mathbb{R}^n$ 등 | 확률변수가 값을 가지는 공간 | 확률변수가 실현값을 내는 수치적 공간 값의 공간 (value space) 사건결과에 매핑되는 수치 공간 확률변수값 또는 확률변수 벡터값의 공간 |
3차원 다변량 정규분포의 등확률밀도 시각화는 신뢰타원체(Confidence ellipsoid) 또는 등밀도타원체(Iso-density ellipsoid)라고 불립니다. 이 시각화는 데이터의 분산 구조, 변수 간 관계, 이상치 탐지 등을 직관적으로 이해하는 데 매우 유용합니다. 등밀 타원체는 확률밀도가 일정한 값을 갖는 지점들의 집합입니다.
타원체의 크기와 방향은 공분산 행렬의 고유값과 고유벡터에 의해 결정됩니다: 고유벡터 축 방향을 나타내고 고유값은 각 축의 길이를 나타냅니다.
Fig1.에 표시된 표면은 약 95%의 확률 질량을 포함하는 등밀도 구역입니다 ($\chi^2$ 분포 기반).
다변량 정규분포 수식
$$f(\mathbf{x}) = \frac{1}{(2\pi)^{3/2} |\boldsymbol{\Sigma}|^{1/2}}
\exp\left( -\frac{1}{2} (\mathbf{x} – \boldsymbol{\mu})^\top
\boldsymbol{\Sigma}^{-1} (\mathbf{x} – \boldsymbol{\mu}) \right)$$
평균벡터
$$\boldsymbol{\mu} =
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}$$
공분산행렬
$$\boldsymbol{\Sigma} =
\begin{bmatrix}
1 & 0.5 & 0.3 \\
0.5 & 1 & 0.4 \\
0.3 & 0.4 & 1
\end{bmatrix}$$
고유값
$$\lambda_1 \approx 0.482, \quad
\lambda_2 \approx 0.7124, \quad
\lambda_3 \approx 1.8056$$
고유벡터
$$\mathbf{V} =
\begin{bmatrix}
-0.5960 & -0.5540 & -0.5813 \\
\;\;\;0.7646 & -0.1704 & -0.6215 \\
-0.2453 & \;\;\;0.8149 & -0.5251
\end{bmatrix}$$
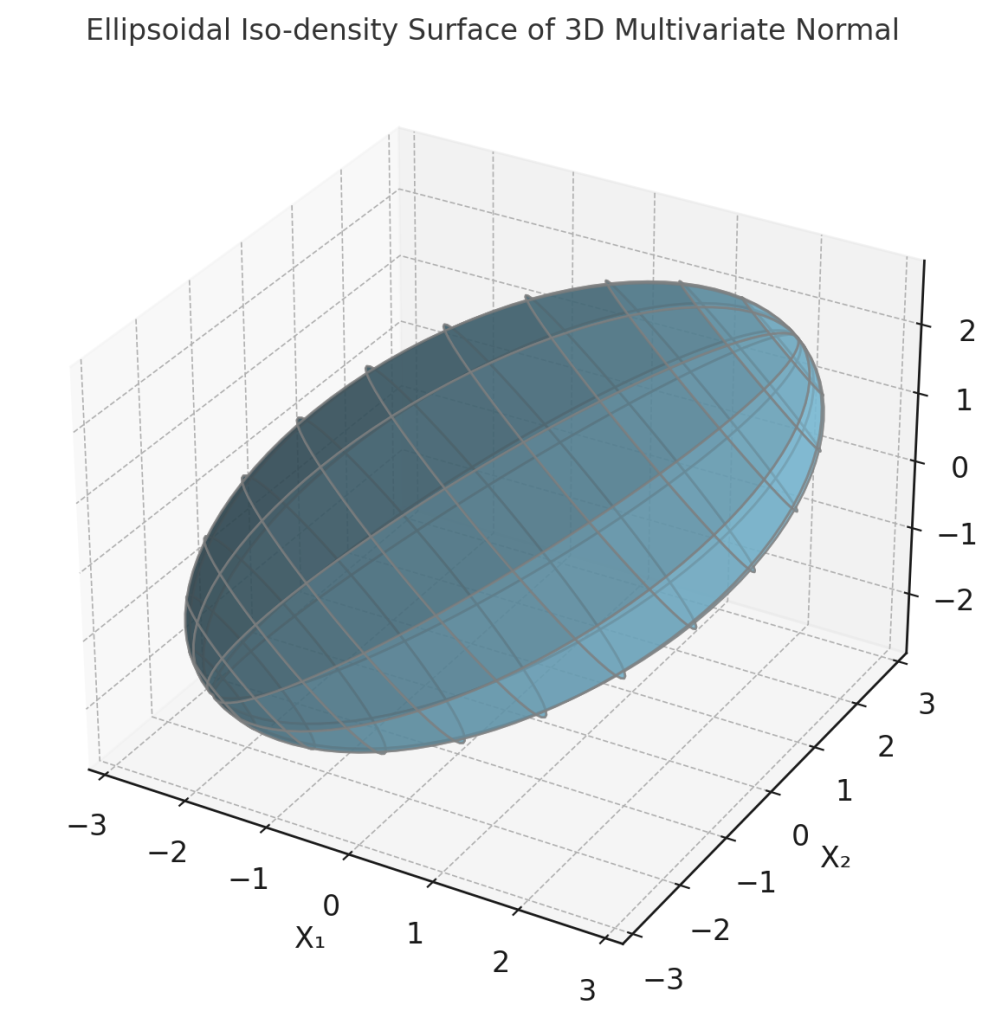
Fig. 1. 3차원 다변량 정규분포의 결합확률분포의 등표면(iso-density surface)
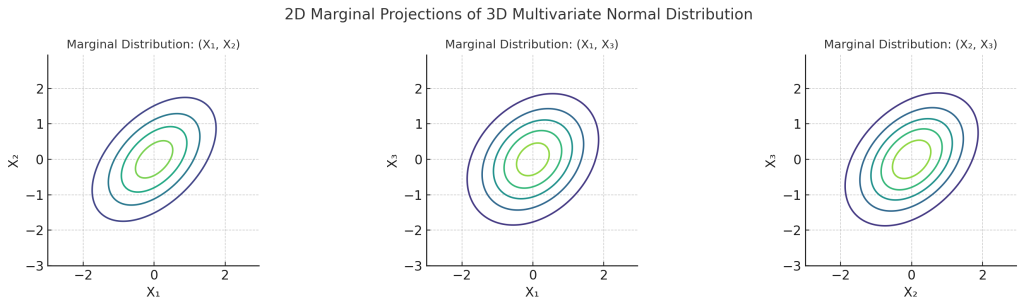
Fig. 2. 3차원 다변량 정규분포의 주변확률분포의 등표면(iso-density surface)
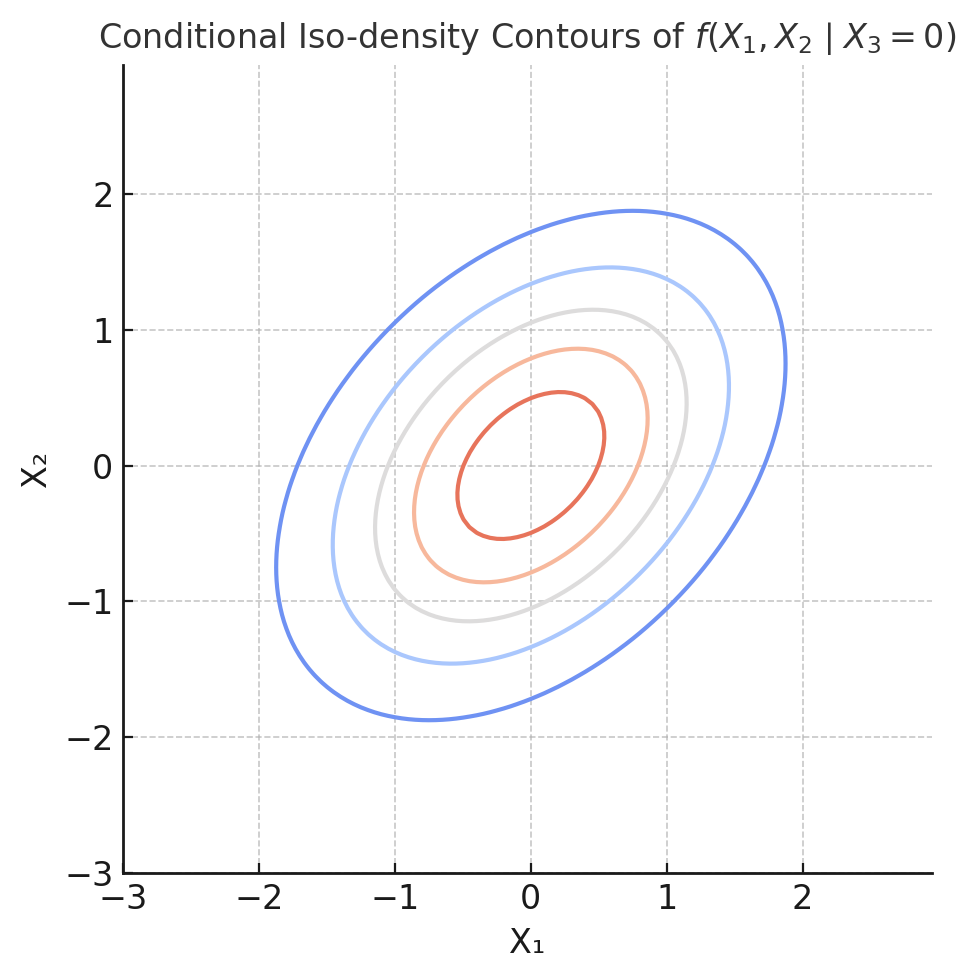
Fig. 3. 3차원 다변량 정규분포의 결합확률분포의 조건부분포 단면, 등확률밀도선(iso-density contours)