DATA SCIENCE : 27
DATA SCIENCE eISSN

[ Q-data science ]

정수, 유리수, 무리수, 실수 수체계(system of numbers) 중에서 연속인 수체계는?

목차

실수입니다.

연속성의 필요성:

  • 연속성이 보장된 실수 함수 위에서만 미분과 적분이 성립됩니다.
  • 시간, 거리, 온도 등의 연속적인 양은 실수로 표현되어야 합니다.
  • 극값을 정의하고 분석하기 위해서는 함수가 연속적이어야 하며, 이러한 연속성은 실수 공간에서 보장됩니다.

1. 수체계

수체계(Number System)는 수학적 연산과 논리 체계 내에서 수의 집합들을 공리적으로 정의하고, 그 위상 및 대수적 구조에 따라 분류한 계층적 구조입니다. 공리적 정의에서 수체계는 집합론 등으로 정의됩니다. 위상 및 대수에서 실수는 연속체이고, 유리수는 체(field), 정수는 환(ring) 등으로 다뤄집니다. 수체계는 계층적 구조로서 자연수 ⊂ 정수 ⊂ 유리수 ⊂ 실수 ⊂ 복소수 등 포함 관계를 나타냅니다.

자연수($\mathbb{N}$)는 1, 2, 3, …처럼 셈을 시작할 때 사용하는 수입니다. “하나, 둘, 셋” 처럼 셀 때 자연수를 사용합니다.

정수($\mathbb{Z}$)는 자연수에 0과 음수를 포함한 수 체계입니다. 즉, …, -3, -2, -1, 0, 1, 2, 3, …과 같이 양의 정수, 음의 정수, 0이 모두 포함됩니다.

유리수($\mathbb{Q}$)는 분수로 나타낼 수 있는 수입니다. 예를 들어 $\dfrac{1}{2}, -\dfrac{5}{3}, 7$ 등은 모두 유리수입니다. 소수로는 유한소수나 반복되는 순환소수의 형태로 나타납니다.

무리수($\mathbb{R} \setminus \mathbb{Q}$)는 유리수가 아닌 실수로, 분수로 표현할 수 없는 수입니다. 대표적인 예로는 $\pi$, $\sqrt{2}$ 등이 있으며, 소수로는 끝나지 않고 반복되지 않는 무한소수 형태를 가집니다.

실수($\mathbb{R}$)는 유리수와 무리수를 모두 포함하는 수직선 전체의 수입니다. 실수는 연속적으로 이어져 있어 끊김 없이 수직선을 완전히 채우는 수 체계입니다. 미적분학 등 연속적인 수학 이론의 기본 바탕이 됩니다.

Table 1. 정수, 유리수, 무리수, 실수의 성질 비교

수체계정의시각화

이산
(Discrete)

[확률]

 

밀도
(Dense)

[근사]

[수렴]

연속
(Continuous)

[적분]

[극한]

가산
(Countable)

[열거]

[순서]

무한
(Infinite)

[극한]

[귀납]

정수

Integers

$\mathbb{Z}$

$\dots, -3, -2, -1, 0, 1, 2, 3, \dots$

수 사이에 빈 공간이 많음

수직선 상의 점OXXOO

유리수

Rational Numbers

$\mathbb{Q}$

$\dfrac{a}{b}$, $a \in \mathbb{Z},\ b \ne 0$

무리수는 포함하지 않음

촘촘하지만 틈이 있음XOXOO

무리수

Irrational Numbers

$\mathbb{R} \setminus \mathbb{Q}$

$\pi$, $\sqrt{2}$ 등 유리수가 아닌 실수

유리수와의 구분이 중요함

유리수와 섞여 있음XOXXO

실수

Real Numbers

$\mathbb{R}$

$\mathbb{Q} \cup (\mathbb{R} \setminus \mathbb{Q})$

무리수가 유리수보다 비교 불가 수준으로 많음

실수 직선 전체XOOXO

2. 수체계 응용

수체계(정수, 유리수, 실수 등)에는 각각 이산성, 밀도성, 연속성, 가산성, 무한성이라는 성질들이 존재합니다. 이들은 단순한 추상 개념이 아니라, 수학적 모델링, 계산, 논리적 추론, 그리고 실세계 응용에서 중요한 역할을 합니다.

1. 이산성 (Discreteness)
이산성은 어떤 두 원소 사이에 그 집합의 다른 원소가 없는 성질을 의미합니다. 정수는 이산적이며 1과 2 사이에 다른 정수가 없음을 볼 때 이산성이 있음을 알 수 있습니다.

  • 컴퓨터 과학에서 디지털 신호나 비트(binary data)는 이산적 개념.
  • 알고리즘 분석에서 이산적 구조(그래프, 순열, 배열 등)가 중요.
  • 정수 프로그램이나 이산 수학에서는 연속적인 수 대신 이산 수가 사용됨.

2. 밀도성 (Density)
밀도성은 임의의 두 수 사이에 항상 그 집합의 또 다른 수가 존재함을 의미합니다. 유리수, 무리수, 실수 수체계의 집합은 밀도가 있습니다.

  • 측정 정밀도 향상: 유리수만으로도 거의 모든 실수를 근사 가능.
  • 수치해석: 유리수 또는 유리 함수로 실수를 근사할 수 있는 이유.
  • 기계 학습에서 모델이 연속 공간을 탐색할 수 있는 이론적 근거.

3. 연속성 (Continuity)
연속성은 수 직선상에서 빈틈 없이 이어져 있음을 의미합니다. 수체계에서 실수만 연속적이며 나머지는 모두 불연속입니다.

  • 미적분학의 전제조건: 미분과 적분은 연속 함수에서 정의.
  • 물리 모델링: 시간, 거리, 온도 등은 연속적인 양으로 간주.
  • 최적화 이론: 연속 공간에서 극값을 찾기 위해 연속성이 요구됨.

4. 가산성 (Countability)
가산성은 집합의 원소들을 자연수와 일대일 대응시킬 수 있음을 의미합니다. 자연수, 정수, 유리수 수체계의 집합은 가산 무한집합이며 실수와 무리수는 비가산성을 가집니다.

  • 컴퓨터 표현: 실제로는 가산 무한 집합만 디지털화 가능.
  • 수리논리학: 어떤 집합이 가산이면 열거 가능(listable) → 알고리즘화 가능.
  • 데이터 구조에서 가산 집합만 다룰 수 있음 (무리수는 직접 저장 불가).

5. 무한성 (Infinity)
무한성은 원소의 수가 유한하지 않음을 의미합니다. 무한성에 기반하여 가산/비가산으로 나뉩니다. 자연수, 정수, 유리수는 가산 무한이며 실수는 비가산 무한입니다.

  • 집합론의 기초: 무한 집합의 분류는 수학의 근본적 문제.
  • 수학적 귀납법: 가산 무한 구조에서 사용 가능.
  • 계산 이론: 가산 집합만 대상으로 계산/코딩 가능 → 비가산 집합은 “비계산 가능성”의 근거.

Table 2. 정수, 유리수, 무리수, 실수의 성질 비교

성질 수체계 수학적 특징
이산 (Discrete) 정수 확률질량 정의 가능, 점들 사이에 간격이 있음
밀도 (Dense) 유리수, 무리수, 실수 임의의 두 수 사이에 항상 원소가 존재, 근사 가능성 있음
연속 (Continuous) 실수 빈틈 없이 수직선을 채움, 적분과 극한이 정의됨
가산 (Countable) 정수, 유리수 원소를 순서대로 나열 가능, 열거 가능함
무한 (Infinite) 정수, 유리수, 무리수, 실수 끝이 없는 크기, 극한 과정과 기수 분류 가능
 

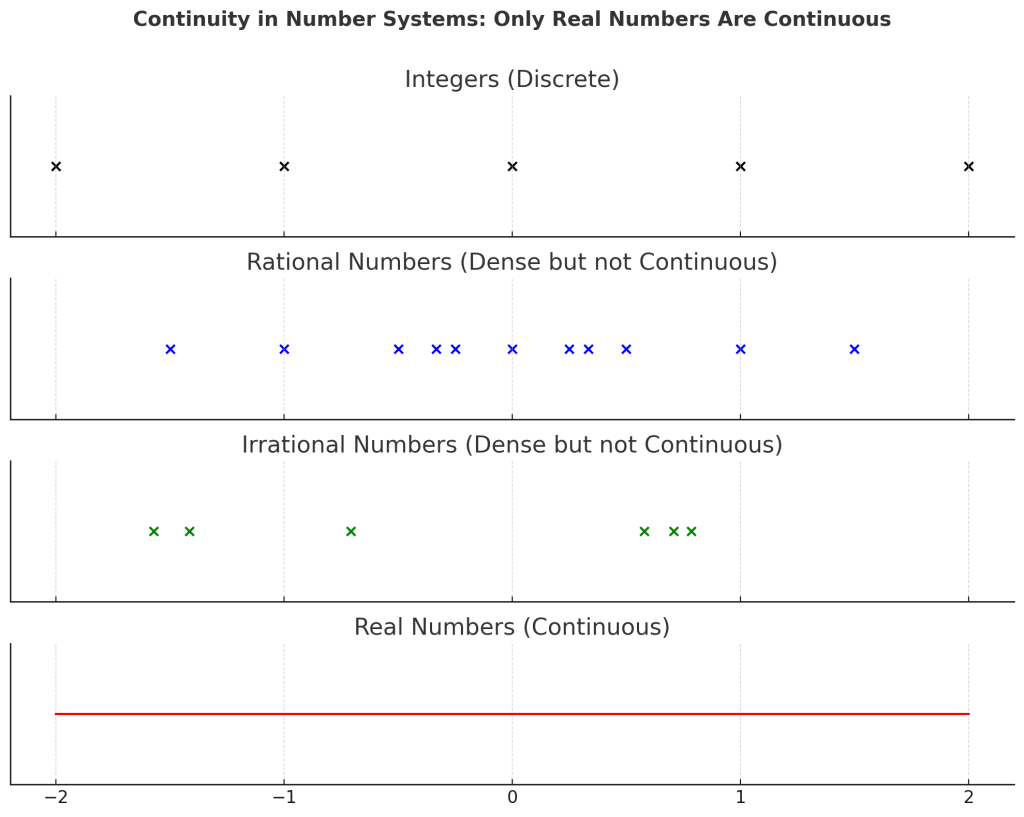
Fig. 1. 수직선 상의 수체계 시각화