집단입니다. 계층구조에서는 집단도 하나의 개체처럼 취급합니다.
계층구조에서는 전체 변동성을 서로 다른 계층(hierarchy, 수준, level)에서의 변동성으로 분해해서 봅니다. 이를 분산의 계층적 분해 (hierarchical variance decomposition) 라고 합니다.
등분산가정 2계층 모델
$$Y_{ij}=\mu+u_j+\epsilon_{ij}$$
여기서, $ Y_{ij}$는 $j$번째 집단에 속한 $i$번째 개체의 관측값
$\mu$는 전체평균
$u_j$는 $j$번째 집단의 오차: $u_j \sim \mathcal{N}(0, \sigma_u^2)$ (등분산가정)
$\epsilon_{ij}$는 $j$번째 집단의 $i$번째 개체의 오차: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_\epsilon^2)$ (등분산가정)
2계층 모델에서 분산분해
개체의 분산 = 전체집단내 집단간 분산 + 집단내 개체간 분산
$$\mathrm{Var}(Y_{ij}) =
\underbrace{\mathrm{Var}(u_i)}_{\text{전체집단내 집단간 분산}}
+
\underbrace{\mathrm{Var}(\epsilon_{ij})}_{\text{집단내 개체간 분산}} = \sigma_u^2 + \sigma_\epsilon^2$$
총변동 분해식(Sum of Squares Decomposition)과 분산 분해식(Variance Decomposition)은 같은 통계적 원리를 다른 관점에서 설명하는 도구입니다. 하나는 통계적, 하나는 확률론적 해석입니다.
총변동 분해식은 측정된 데이터의 변동을 숫자로 계산한 것이고, 분산 분해식은 확률변수의 조건부 평균과 조건부 분산으로 이루어진 구조를 수학적으로 분해한 것입니다.
예를 들어, 총변동 분해식은 데이터 기반으로 “학생의 시험 점수 데이터에서, 각 점수가 전체 평균 또는 반의 평균으로부터 얼마나 떨어져 있는지를 제곱하여 합산한 값 — 즉, 실제 관측값을 기반으로 변동성을 측정한 것”입니다. 분산 분해식은 “학생의 점수 차이가, 반 간 평균의 차이 때문인지, 같은 반 안의 학생들 간 차이 때문인지를 이론적으로(확률적으로) 분해한 것”입니다.
$$SS_T = \sum_{i=1}^n (Y_i – \bar{Y})^2 =\underbrace{\sum_{j=1}^k n_j (\bar{Y}_j – \bar{Y})^2}_{SS_B} +
\underbrace{\sum_{j=1}^k \sum_{i=1}^{n_j} (Y_{ij} – \bar{Y}_j)^2}_{SS_W}$$
제곱합을 자유도로 나누어 분산의 형태로 정규화 – 표본이 전체집단인 경우
$$s^2
= \underbrace{\frac{SS_T}{n – 1}}_{\text{분산 추정}}
= \underbrace{\frac{SS_B}{k – 1}}_{\text{전체집단내 집단간 분산}}
+ \underbrace{\frac{SS_W}{n – k}}_{\text{집단내 개체간 분산}}$$
여기서, $s^2$ 은 표본분산
$n$은 표본내 개체수
$k$는 표본내 집단수
조건부 확률변수로 일반화
$$\mathrm{Var}(Y)
= \underbrace{\mathrm{Var}(\mathbb{E}[Y \mid G])}_{\text{집단간분산}}
+ \underbrace{\mathbb{E}[\mathrm{Var}(Y \mid G)]}_{\text{집단내분산}}$$
Table 1. 총변동 분해식와 분산 분해식 비교
| 항목 | 총변동 분해식 | 분산 분해식 |
|---|---|---|
| 수식 | $$\mathrm{SS_T} = \mathrm{SS_B} + \mathrm{SS_W}$$ 여기서, SST: 총제곱합 (Total Sum of Squares) | $$\mathrm{Var}(Y) = \mathrm{Var}(\mathbb{E}[Y \mid G]) + \mathbb{E}[\mathrm{Var}(Y \mid G)]$$ 여기서, \(Y\): 관측값 |
| 사용 분야 | ANOVA, 실험통계 | 확률이론, 계층모형 |
| 주요 개념 | 제곱합 (Sum of Squares) | 분산 (Variance) |
| 설명 | 데이터기반으로 표본값의 제곱합 | 확률 변수의 이론적 구조 |
| 해석 | 실제 관측값의 차이 | 조건부 평균과 조건부 분산의 구조 |
| 적용 예 | 분산분석(F-test), 회귀분석의 $SS_E$, $SS_R$ | 혼합효과모형, 다층모형, 베이지안 모형 등 |
BLUP은 혼합선형모형에서 개체 수준의 반응값 $Y_i$를 고정효과와 확률효과로 나누는 모델입니다.
$$Y_i = \mu + u_i + \epsilon_i$$
여기서, $Y_i $: 개체 $i$의 표현형 관측값
$\mu$: 전체 평균 (고정효과)
$u_i \sim N(0, \sigma_u^2) $: 개체별 육종가 (확률효과 = 개체가 속한 집단)
$\epsilon_i \sim N(0, \sigma_\epsilon^2)$: 개체 수준 오차
이 모델의 전체 분산은 다음과 같이 분해됩니다:
$$\mathrm{Var}(Y_i) =
\underbrace{\mathrm{Var}(u_i)}_{\sigma_u^2\ \text{(육종가 분산)}} +
\underbrace{\mathrm{Var}(\epsilon_i)}_{\sigma_\epsilon^2\ \text{(오차 분산)}}=\mathrm{Var}(Y_i) = \sigma_u^2 + \sigma_\epsilon^2$$
개체의 표현형은 전체 평균 + 유전적 차이 + 환경 오차로 구성되며, 그 총 분산은 유전적 분산 + 환경 분산의 합으로 설명됩니다.
BLUP는 다음과 같은 혼합 선형모형(mixed linear model)에서 나타납니다.
$$\mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \mathbf{Z} \mathbf{u} + \boldsymbol{\epsilon}$$
여기서, $\mathbf{Y}$는 관측값 벡터 (response vector)
$\mathbf{X}$는 고정효과 설계행렬 (design matrix for fixed effects)
$\boldsymbol{\beta}$는 고정효과 계수 벡터 (fixed effects vector)
$\mathbf{Z}$는 랜덤효과 설계행렬 (design matrix for random effects)
$\mathbf{u}$는 랜덤효과 벡터 (random effects vector)
$\boldsymbol{\epsilon}$는 오차항 벡터 (residual errors)
Table 1. BLUP/혼합모형의 수식 구성과 계층
| 항 | 의미 | 계층 수준 |
|---|---|---|
| $Y$ | 관측값 (예: 개체의 성적, 생산량 등) | 1수준 (개체) |
| $X\beta$ | 고정효과 (예: 성별, 연도 등) | 1수준 (전체 공통 효과) |
| $\mathbf{Z}\mathbf{u}$ | 확률효과 (random effect), 예: 개체별 육종가 | 2수준 (개체가 속한 집단) |
| $\epsilon$ | 오차항 | 1수준 (개체 고유 오차) |
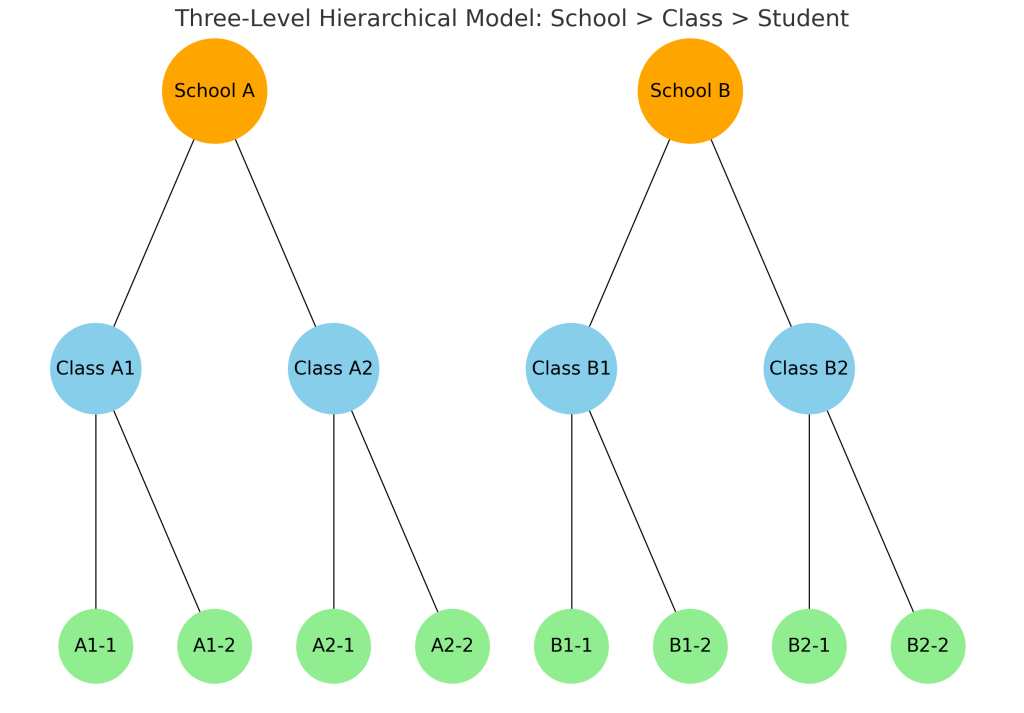
Fig. 1. 개체와 집단의 계층모델