예측(prediction)합니다.
혼합선형모델(LLM)에서 고정효과는 모델의 구조를 설명하는 상수이고, 랜덤효과는 각 집단의 편차를 예측한 확률변수값이며 모델을 보정합니다.
혼합선형모델에서 고정효과인 모수를 BLUE로 추정하고 랜덤효과인 확률변수값을 BLUP로 예측합니다.
혼합선형모델에서 고정효과와 랜덤효과는 함께 작동하며, 고정효과를 추정한 후 랜덤효과를 예측하여 전체 모델이 완성됩니다.
고정효과(fixed effects) 선형모델(linear model)은 모든 효과를 고정된 상수(모수)로 간주하여 구성된 선형모델입니다. 이 모델은 집단 간 차이를 명시적으로 추정하고 비교할 때 사용됩니다. 교육학에서는 이 모델을 고정인터셉트모델 또는 분산분석(Analysis of variance, ANOVA)형 고정효과 선형모델이라고 부릅니다. 고정효과 선형모델은 혼합선형모델(Linear Mixed Model, LMM)의 특수한 형태입니다. 혼합선형모델의 모든 요인이 고정효과일 때 이 특수한 혼합선형모델을 고정효과 선형모델이라고 합니다.
$$y_{ij} = \mu + \beta_j + \epsilon_{ij}$$
여기서, $y_{ij}$는 $i$번째 집단의 $j$번째 개체의 관측값
$\mu$는 전체평균(고정효과)
$\beta_i$는 $i$번째 고정효과의 기여
$\epsilon_{ij}$는 $i$번째 집단의 $j$번째 개체의 오차: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$
고정효과 선형모델의 확률-통계모델식은 다음과 같습니다.
$$\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon}$$
여기서, $\mathbf{y}$는 반응변수벡터(종속변수벡터): $n\times 1$
$n$은 개체 수
$\mathbf{X}$는 고정효과 설계행렬: $n\times p$
$p$는 전체평균포함한 고정효과의 수
$\boldsymbol{\beta}$는 고정효과 계수벡터(전체평균 $\mu$포함): $p\times 1$
$\boldsymbol{\epsilon}$는 오차벡터 $n\times 1$
Table 1. 고정효과 선형모델에서의 추정과 예측
| 구분 | 추정 (Estimation) | 예측 (Prediction) |
|---|---|---|
| 대상 | 모델의 고정값(모수): $\mu$, $\beta_i$ or $\boldsymbol{\beta}$ → $\hat{\mu}$, $\hat{\beta_i}$ or $\hat{\boldsymbol{\beta}}$ | 미지의 관측값: $y_{ij}$ or $\mathbf{y}$ → $\hat{y_{ij}}$ or $\hat{\mathbf{y}}$ |
| 본질 | 고정된 값을 추정 | 실현값을 예측 |
| 방법 | BLUE 등 | 고정효과 추정값 기반 예측 |
| 불확실성 | 표준오차 존재 | 표준오차 + 예측오차 존재 |
| 대상 | 모델의 고정된 계수 | 새로운 상황의 결과값 |
| 구하는 목적 | 고정된 값을 몰라서 구함 | 실현될 값을 미리 알기 위해 구함 |
| 다시 관측하면 같은가? | 네 (고정됨) | 아니오 (바뀔 수 있음) |
랜덤효과(random effects) 선형모델(linear model)은 고정효과는 절편 $\mu$이고 랜덤효과는 집단별 편차 $u_i$인 두 효과로 구성된 단순혼합선형모델입니다. 교육학에서는 랜덤인터셉트모델이라고도 부릅니다. 이 모델은 1-way ANOVA 모델에서 집단효과를 랜덤효과로 모델링한 경우입니다. 혼합선형모델(LMM)의 특수한 형태로 고정효과는 절편만 있습니다.
하나의 랜덤효과만 포함된 가장 단순한 선형모델을 단일수준 랜덤효과 선형모델이라고도 부르며 확률모델식은 다음과 같습니다.
$$y_{ij} = \mu + u_i + \epsilon_{ij} \quad u_i \sim \mathcal{N}(0, \sigma_u^2), \,\, \epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$$
여기서, $y_{ij}$는 $i$번째 집단의 $j$번째 개체의 관측값
$\mu$는 전체평균(고정효과)
$u_i$는 $i$번째 집단의 편차(랜덤효과): $u_i \sim \mathcal{N}(0, \sigma_u^2)$
$\epsilon_{ij}$는 개체별 오차: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$
단일수준 랜덤효과 선형모델의 확률-통계모델식은 다음과 같습니다.
$$\mathbf{y} = $\mathbf{1_n}$ \mu + \mathbf{Z} \mathbf{u} + \boldsymbol{\epsilon}$$
여기서, $\mathbf{y}$는 반응변수벡터(종속변수벡터): $n\times 1$
$n$은 개체 수
$\mathbf{1_n}$는 랜덤효과 선형모델의 고정효과 설계벡터: 모든 원소가 1인 벡터 $n\times 1$ $\mathbf{X}$=$\mathbf{1_n}$
$\mu$는 전체평균(스칼라양)
$\mathbf{Z}$는 랜덤효과 설계행렬: $n\times q$
$q$는 집단 수
$\mathbf{u}$는 랜덤효과 벡터: $q\times 1$
$\boldsymbol{\epsilon}$는 오차벡터 $n\times 1$
Table 2. 단일수준 랜덤효과 선형모델에서의 추정과 예측
| 구분 | 추정 (Estimation) | 예측 (Prediction) |
|---|---|---|
| 대상 | 모델의 고정값(모수) $\mu$ → $\hat{\mu}$ | 미지의 확률값 또는 관측값 $u_i$, $y_{ij}$ or $\mathbf{u}$, $\mathbf{y}$ → $\hat{u_i}$, $\hat{y_{ij}}$ or $\hat{\mathbf{u}}$, $\hat{\mathbf{y}}$ |
| 본질 | 고정된 값을 추정 | 새로운 값 또는 실현값을 예측 |
| 방법 | BLUE 등 | BLUP 등 |
| 불확실성 | 표준오차 존재 | 표준오차 + 예측오차 존재 |
| 대상 | 모델의 고정된 계수 | 새로운 상황의 결과값 |
| 구하는 목적 | 고정된 값을 몰라서 구함 | 실현될 값을 미리 알기 위해 구함 |
| 다시 관측하면 같은가? | 네 (고정됨) | 아니오 (바뀔 수 있음) |
혼합선형모델(Linear Mixed Model, LMM)은 고정효과와 랜덤효과를 결합한 선형모델입니다.
혼합선형모델의 확률모델식은 다음과 같습니다.
$$y_{ij} = \mu + \beta_i+u_i + \epsilon_{ij} \quad u_i \sim \mathcal{N}(0, \sigma_u^2), \,\, \epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$$
여기서, $y_{ij}$는 $i$번째 집단의 $j$번째 개체의 관측값
$\mu$는 전체평균(고정효과)
$\beta_i$는 $i$번째 고정효과의 기여
$u_i$는 $i$번째 집단의 편차(랜덤효과): $u_i \sim \mathcal{N}(0, \sigma_u^2), $
$\epsilon_{ij}$는 개체별 오차: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$
혼합선형모델의 확률-통계모델식은 다음과 같습니다.
$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z} \mathbf{u} + \boldsymbol{\epsilon}$$
여기서, $\mathbf{y}$는 반응변수벡터(종속변수벡터): $n\times 1$
$n$은 개체 수
$\mathbf{X}$는 고정효과 설계행렬: $n\times p$
$p$는 전체평균포함한 고정효과의 수
$\boldsymbol{\beta}$는 고정효과 계수벡터(전체평균 $\mu$포함): $p\times 1$
$\mathbf{Z}$는 랜덤효과 설계행렬: $n\times q$
$q$는 집단 수
$\mathbf{u}$는 랜덤효과 벡터: $q\times 1$
$\boldsymbol{\epsilon}$는 오차벡터 $n\times 1$
Table 3. 혼합선형모델에서의 추정과 예측
| 구분 | 추정 (Estimation) | 예측 (Prediction) |
|---|---|---|
| 대상 | 모형의 고정값(모수) $\mu$, $\beta_i$ or $\boldsymbol{\beta}$ → $\hat{\mu}$, $\hat{\beta_i}$ or $\hat{\boldsymbol{\beta}}$ | 미지의 확률값 또는 관측값 $u_i$, $y_{ij}$ or $\mathbf{u}$, $\mathbf{y}$ → $\hat{u_i}$, $\hat{y_{ij}}$ or $\hat{\mathbf{u}}$, $\hat{\mathbf{y}}$ |
| 본질 | 고정된 값을 추정 | 새로운 값 또는 실현값을 예측 |
| 방법 | BLUE 등 | BLUP 등 |
| 불확실성 | 표준오차 존재 | 표준오차 + 예측오차 존재 |
| 대상 | 모형의 고정된 계수 | 새로운 상황의 결과값 |
| 구하는 목적 | 고정된 값을 몰라서 구함 | 실현될 값을 미리 알기 위해 구함 |
| 다시 관측하면 같은가? | 네 (고정됨) | 아니오 (바뀔 수 있음) |
고정효과 선형모델은 선생님 각각의 효과를 고정된 수치로 모델링합니다.
$$y_{ij} = \mu + \beta_i + \epsilon_{ij}$$
여기서, $y_{ij}$는 $i$번째 선생님에게 배정된 $j$번째 학생의 성적
$\mu$는 전체평균성적: 모든 학생의 기준
$\beta_i$는 $i$번째 선생님의 고정된 기여효과: BLUE로 추정
$\epsilon_{ij}$는 학생의 개별 오차항: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$
$i$번째 선생님의 효과를 고정된 수치 $\hat{\beta_i}$로 추정하고 새로운 학생의 성적 $\hat{y_{ij}}$의 예측값 또는 관측된 학생의 적합값(fitted value)은 다음식으로 표현됩니다.
$$\hat{y_{ij}}=\hat{\mu}+\hat{\beta_i}$$
랜덤효과 선형모델은 선생님 효과를 확률적으로 실현되는 편차로 봅니다. 랜덤효과를 선생님의 학생성적에 끼치는 효과로 보고 평균이 0이고 분산이 $sigma_u^2$인 정규분포로 모델링합니다.
$$y_{ij} = \mu + u_i + \epsilon_{ij}$$
여기서, $y_{ij}$는 $i$번째 선생님에게 배정된 $j$번째 학생의 성적
$\mu$는 전체평균성적: 모든 학생의 기준
$u_i$는 $i$번째 선생님의 랜덤효과로 BLUP로 추정: $u_i \sim \mathcal{N}(0, \sigma_u^2)$
$\epsilon_{ij}$는 학생의 개별 오차항: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_e^2)$
$i$번째 선생님의 효과를 확률적으로 실현되는 편차로 보고 평균 0, 분산 $\sigma_u^2$으로 설명합니다. 학생의 성적 $\hat{y_{ij}}$를 예측은 다음식으로 모델링됩니다.
$$\hat{y_{ij}}=\hat{\mu}+\hat{u_i}$$
고정효과 선형모델은 각 선생님의 효과를 명확히 추정하여 비교하고 싶을 때 적합하며, 랜덤효과 선형모델은 선생님 수가 많고 정확한 예측이나 분산 분석이 목표일 때 적합합니다.
Table 2. 학생 성적 예측을 위한 고정효과 선형모델과 랜덤효과 선형모델의 비교
| 항목 | 고정효과모델 | 랜덤효과모델 |
|---|---|---|
| 선생님 효과 | 상수 \( \beta_i \) 추정 | 확률 \( u_i \) 예측 |
| 목적 | 선생님 차이 분석 | 성적 예측 정확도 |
| 선생님 수 | 적을 때 적합 | 많을 때 적합 |
| 새로운 선생님 예측 | 불가 | 가능, 구간추정 |
| 학생 성적 예측 | $ \mu + \beta_i $ 구간추정 $$\hat{y}_{ij} = \hat{\mu} + \hat{\beta}_i | $\mu + u_i $ 구간추정 $$\hat{y}_{ij} = \hat{\mu} + \hat{u}_i |
| 추정 방식 | BLUE | BLUP |
| 오차 구조 | \( \sigma_e^2 \) | \( \sigma_u^2 + \sigma_e^2 \) |
선생님 수(집단 수)가 많아지면 랜덤효과 분산 추정의 정확도는 증가합니다. 그 결과 BLUP 수축이 더 신뢰성 있게 계산됩니다.
수축(shrinkage)의 크기 자체는 선생님 수가 아니라, 각 선생님에 배정된 학생 수에 따라 결정됩니다. 배정된 학생 수가 클수록 수축(shrinkage)은 작게 일어납니다. BLUP는 랜덤효과 예측값 $\hat{u_i}$를 항상 0에 가까운 값으로 수축(shrink)시킵니다. 수축 정도는 다음 수축계수로 표현됩니다.
$$\text{Shrinkage factor} = \frac{n_i}{n_i + \lambda}, \quad \text{where} \ \lambda = \frac{\sigma_e^2}{\sigma_u^2}$$
여기서, $n_i$는 $i$번째 선생님에게 배정된 학생 수
$\lambda$는 오차 대비 랜덤효과의 비율
$\sigma_e^2$는 학생 오차 분산
$\sigma_u^2$는 선생님 간 효과 분산
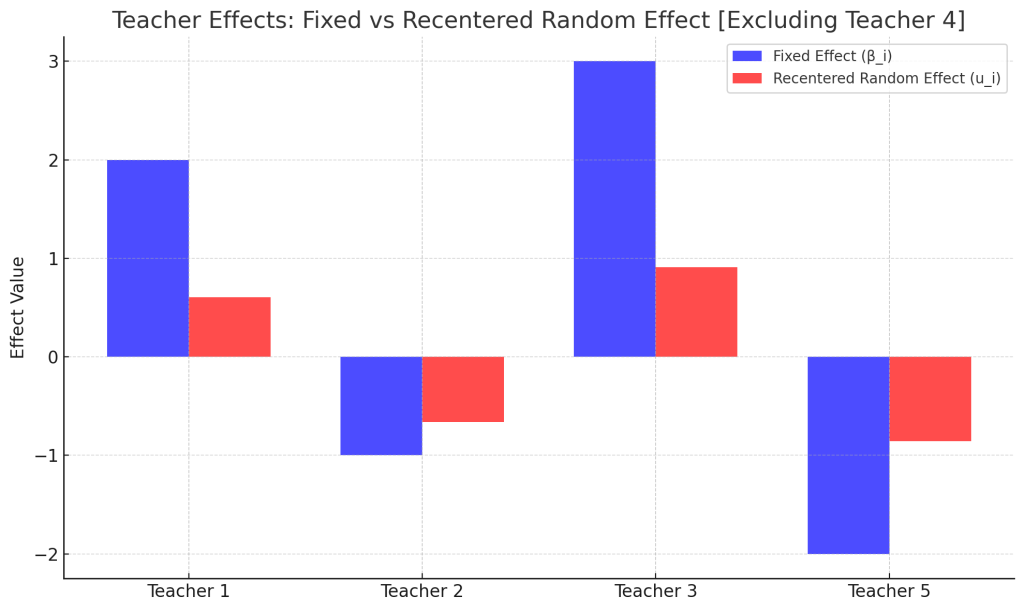
Fig. 1. 선생님별 효과 비교: 고정효과 vs 랜덤효과
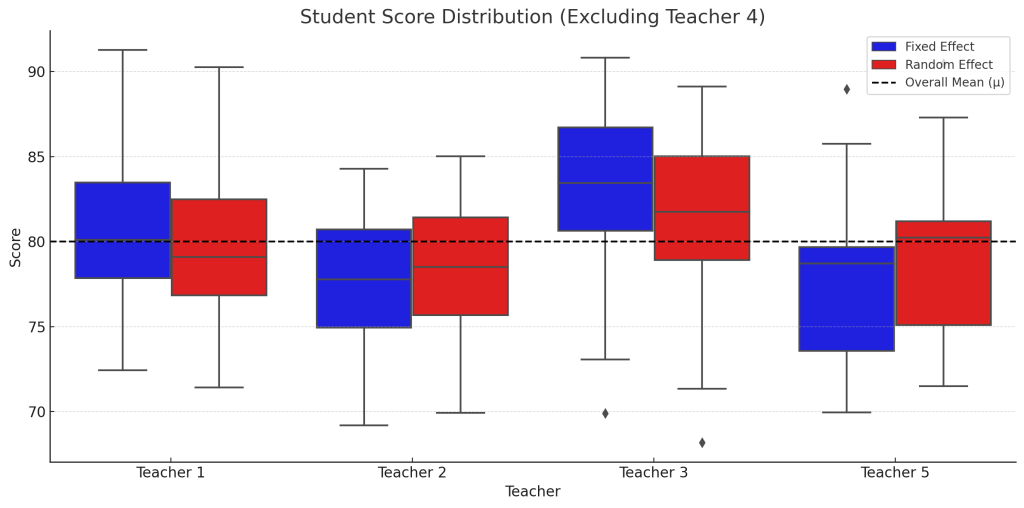
Fig. 2. 고정효과와 랜덤효과에 따른 학생 성적 분포 비교