네 추정량에 영향을 줍니다.
$$\hat{\boldsymbol{\beta}}
= \left(\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{X}\right)^{-1}
\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{y}$$
여기서, $\hat{\boldsymbol{\beta}}$는 고정효과벡터의 추정량
$\mathbf{V}$는 반응변수벡터 $\mathbf{y}$의 분산-공분산행렬
혼합선형모델에서 반응변수의 분산은 고정효과벡터 추정량의 기대값 $\mathrm{E}[\hat{\boldsymbol{\beta}}]$에는 영향을 주지 않습니다.
$$\mathrm{E}[\hat{\boldsymbol{\beta}}]=\boldsymbol{\beta}$$
모평균은 상수이고 표본평균은 표본추출에 따라 값이 변하는 확률변수입니다. 그러나 표본평균을 관측값(상수)으로 고정하면, 모평균은 그 값을 중심으로 분포를 가지는 추정량의 형태로 해석하는 것과 같은 이치입니다.
혼합선형모델에서 “반응변수의 분산–공분산행렬” $\mathbf{V}$는 “랜덤효과의 분산–공분산행렬” $\mathbf{G}$를 설계행렬 $\mathbf{Z}$를 통해 관측공간으로 변화한 $\mathbf{ZGZ}^\mathsf{T}$와 “오차항의 분산–공분산행렬” $\mathbf{R}$의 합으로 주어집니다.
$$\mathbf{V} = \mathbf{Z}\,\mathbf{G}\,\mathbf{Z}^\mathsf{T} + \mathbf{R}$$
여기서, $\mathbf{V}$는 반응변수의 분산–공분산행렬
$\mathbf{Z}$는 랜덤효과 설계행렬
$\mathbf{G}$는 랜덤효과의 분산–공분산행렬
$\mathbf{R}$는 오차항의 분산–공분산 행렬
고정효과 선형모델 (fixed effect linear model): OLS(Ordinary Least Square, 보통최소제곱)의 확률-통계모델
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},
\quad \boldsymbol{\varepsilon} \sim N\left(\mathbf{0}, \sigma^2 \mathbf{I}_n\right)
\]
반응변수 $\mathbf{y}$의 분산-공분산행렬 $\mathbf{V}$
\[
\mathbf{V} = \mathrm{Var}(\mathbf{y}) = \sigma^2 \mathbf{I}_n
\]
고정효과벡터 $\boldsymbol{\beta}$추정
\[
\hat{\boldsymbol{\beta}}
= \left(\mathbf{X}^\mathsf{T} \mathbf{X}\right)^{-1}
\mathbf{X}^\mathsf{T} \mathbf{y}
\]
고정효과에서 $\mathbf{V}$의 역할
등분산·독립 구조이므로 모든 관측값에 동일한 가중치를 부여합니다.
고정효과 선형모델 (fixed effect linear model): GLS(General Least Square, 일반최소제곱)의 확률-통계모델
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},
\quad \boldsymbol{\varepsilon} \sim N\left(\mathbf{0}, \mathbf{R}\right)
\]
반응변수 $\mathbf{y}$의 분산-공분산행렬 $\mathbf{V}$
\[
\mathbf{V} = \mathrm{Var}(\mathbf{y}) = \mathbf{R}
\]
고정효과벡터 $\boldsymbol{\beta}$추정
\[
\hat{\boldsymbol{\beta}}
= \left(\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{X}\right)^{-1}
\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{y}
\]
고정효과에서 $\mathbf{V}$의 역할
오차가 이분산 또는 상관 구조를 가지므로 $\mathbf{V}$의 역행렬이 관측값의 가중치 및 상관보정 역할을 합니다.
랜덤효과 선형모델 (random effect linear model)의 확률-통계모델
\[
\mathbf{y} = \mu\mathbf{1} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon},
\quad \mathbf{u} \sim N\left(\mathbf{0}, \mathbf{G}\right), \quad
\boldsymbol{\varepsilon} \sim N\left(\mathbf{0}, \mathbf{R}\right)
\]
반응변수 $\mathbf{y}$의 분산-공분산행렬 $\mathbf{V}$
\[
\mathbf{V} = \mathrm{Var}(\mathbf{y}) = \mathbf{Z}\mathbf{G}\mathbf{Z}^\mathsf{T} + \mathbf{R}
\]
고정효과벡터 $\boldsymbol{\beta}$추정
\[
\hat{\boldsymbol{\beta}}=\hat{\mu}
= \left(\mathbf{1}^\mathsf{T} \mathbf{V}^{-1} \mathbf{1}\right)^{-1}
\mathbf{1}^\mathsf{T} \mathbf{V}^{-1} \mathbf{y}
\]
고정효과에서 $\mathbf{V}$의 역할
랜덤효과에 의한 변동 $\mathbf{ZGZ}^T$과 오차항 변동 $\mathbf{R}$을 모두 반영하여, 군집 구조나 상관성을 고려한 가중 평균을 산출합니다.
혼합선형모델(LMM, Linear Mixed Model)의 확률-통계모델
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\mathbf{u} + \boldsymbol{\varepsilon},
\quad \mathbf{u} \sim N\left(\mathbf{0}, \mathbf{G}\right), \quad
\boldsymbol{\varepsilon} \sim N\left(\mathbf{0}, \mathbf{R}\right)
\]
반응변수 $\mathbf{y}$의 분산-공분산행렬 $\mathbf{V}$
\[
\mathbf{V} = \mathrm{Var}(\mathbf{y}) = \mathbf{Z}\mathbf{G}\mathbf{Z}^\mathsf{T} + \mathbf{R}
\]
고정효과벡터 $\boldsymbol{\beta}$추정
\[
\hat{\boldsymbol{\beta}}
= \left(\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{X}\right)^{-1}
\mathbf{X}^\mathsf{T} \mathbf{V}^{-1} \mathbf{y}
\]
고정효과에서 $\mathbf{V}$의 역할
등분산·독립 구조이므로 모든 관측값에 동일한 가중치를 부여합니다.
Table 2. OLS, GLS, 랜덤효과, LMM 비교
선형모델 (LM) | 반응변수의 분산-공분산행렬 \( \mathbf{V} \) | 고정효과벡터의 추정량 \( \hat{\boldsymbol{\beta}} \) | \( \mathbf{V} \)의 역할 |
|---|---|---|---|
| 고정효과-OLS | \( \mathbf{V} = \sigma^2 \mathbf{I}_n \) | \( \hat{\boldsymbol{\beta}} = \big(\mathbf{X}^\mathsf{T}\mathbf{X}\big)^{-1}\mathbf{X}^\mathsf{T}\mathbf{y} \) | 모든 관측값에 동일 가중치 |
| 고정효과-GLS | \( \mathbf{V} = \mathbf{R} \) | \( \hat{\boldsymbol{\beta}} = \big(\mathbf{X}^\mathsf{T}\mathbf{V}^{-1}\mathbf{X}\big)^{-1}\mathbf{X}^\mathsf{T}\mathbf{V}^{-1}\mathbf{y} = \big(\mathbf{X}^\mathsf{T}\mathbf{R}^{-1}\mathbf{X}\big)^{-1}\mathbf{X}^\mathsf{T}\mathbf{R}^{-1}\mathbf{y} \) | 상관·이분산 보정, 가중치 부여 |
| 랜덤효과 | \( \mathbf{V} = \mathbf{Z}\mathbf{G}\mathbf{Z}^\mathsf{T} + \mathbf{R} \) | \( \hat{\boldsymbol{\beta}}=\hat{\mu} = \big(\mathbf{1}^\mathsf{T}\mathbf{V}^{-1}\mathbf{1}\big)^{-1}\mathbf{1}^\mathsf{T}\mathbf{V}^{-1}\mathbf{y} \) | 군집/상관 구조 반영, 가중 평균 |
혼합 (LMM) | \( \mathbf{V} = \mathbf{Z}\mathbf{G}\mathbf{Z}^\mathsf{T} + \mathbf{R} \) | \( \hat{\boldsymbol{\beta}} = \big(\mathbf{X}^\mathsf{T}\mathbf{V}^{-1}\mathbf{X}\big)^{-1}\mathbf{X}^\mathsf{T}\mathbf{V}^{-1}\mathbf{y} \) | 랜덤효과·오차 변동 모두 반영, 고정효과 추정 가중치 제공 |
프리퀀티스(frequentist)는 빈도론자입니다. “현실”(data)을 보고 “미지의 세계”(모집단)를 상상하는 사람들입니다. 즉, 표본분포(sampling distribution)를 통해 모수를 추정합니다. 베이지안(baysian)은 프랑스수학자 베이즈를 추종하는 사람들로 모집단(미지의 세계)를 가정한 뒤 데이터(현실)로 수정하는 사람들입니다. 즉, 모수 자체를 확률변수로 두고 불확실성을 수치화합니다.
Table 2. 프리퀀티스와 베이지안의 표본평균과 모평균 관점 비교
| 구분 | 빈도론자 (Frequentist) | 베이지안 (Bayesian) |
|---|---|---|
| 모평균 \( \mu \) | 모집단에서 고정된 상수(확률변수 아님) | 사전분포(prior)를 가지는 확률변수 |
| 표본평균 \( \overline{X} \) | 표본추출에 따라 변하는 확률변수 | 관측 후에는 고정된 값(데이터) |
| 추론 방식 | 표본평균의 표본분포(sampling distribution)를 이용해 모평균 추정 | 모평균의 사후분포(posterior distribution)를 이용해 추정 |
| 해석 예시 | \( \overline{X} \)가 변하므로, \( \mu \) 추정치는 표본마다 다르다. | 관측된 \( \overline{X} \)를 바탕으로, \( \mu \)는 다음과 같은 확률분포를 가진다. |
| 분포의 대상 | \( \overline{X} \) (확률변수) | \( \mu \) (확률변수) |
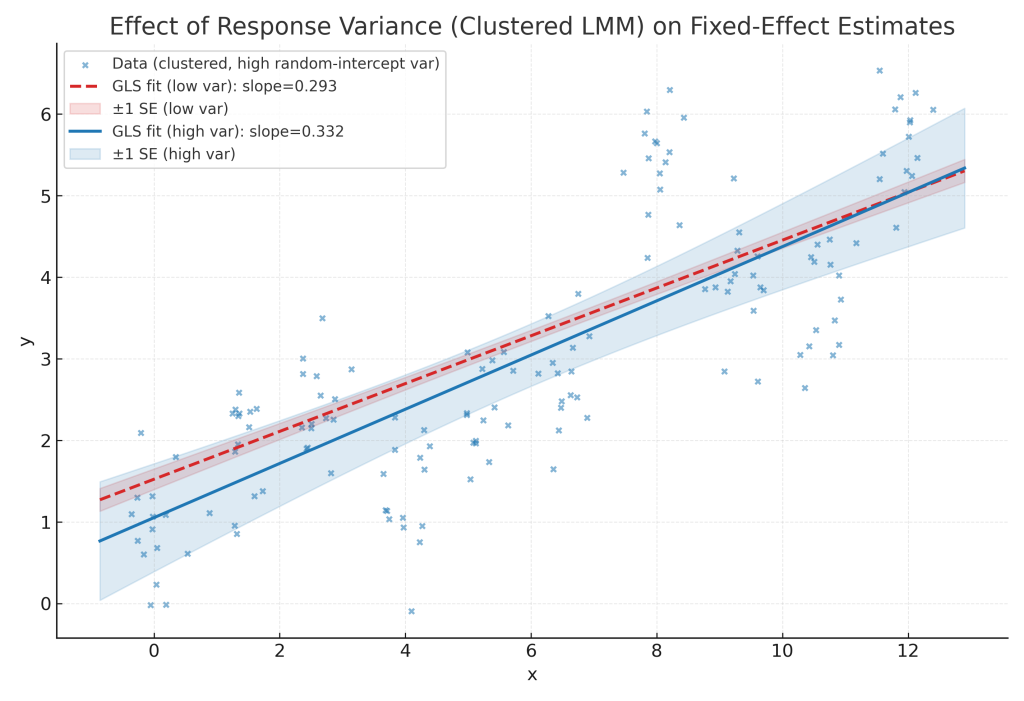
Fig. 1. 고정효과 선형: GLS 모델에서 반응변수 분산이 고정효과 추정량에 미치는 영향 비교