네. 독립변수가 무작위로 관측되면 독립변수를 확률변수로 봅니다.
반면, 독립변수를 고정값으로 보는 경우는 독립변수를 연구자가 정할 때입니다. 예를 들어 농업실험이나 임상시험에서 실험조건을 연구자가 정하는 경우입니다.
고정효과 선형모델에서 독립변수를 확률변수로 두면, 현실적 데이터 구조(샘플링·상관성)를 더 잘 반영하고, 특히 일반화 가능성과 예측력이 향상됩니다. 따라서 확률독립변수(Random-X)는 관측 데이터 분석에 더 자연스럽습니다. 반면, 고정독립변수(Fixed-X)는 독립변수를 연구자가 조정하는 설계 기반 실험에 적합합니다.
고정독립변수 선형모델은 독립변수를 연구자가 설계한 값으로 간주하여, 조건부분포 $\mathbf{y} \mid \mathbf{X}$만을 고려합니다. 이때 회귀계수 추정량의 분산은 $\sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1}$ 으로 단순하며, 주어진 $\mathbf{X}$ 에 국한된 예측을 제공합니다. 반면 확률독립변수 모델은 $\mathbf{X}$를 모집단에서 추출된 확률변수로 보아 $f(\mathbf{y}, \mathbf{X}) = f(\mathbf{y} \mid \mathbf{X}) f(\mathbf{X})$의 결합분포로 접근합니다. 이 경우 추정량의 분산은 $ \sigma^2 \mathbb{E}[(\mathbf{X}^\top \mathbf{X})^{-1}] $이 되어 더 현실적이며, 새로운 표본에 대한 일반화 예측력이 강화됩니다.
Table 1. 고정독립변수와 확률독립변수의 비교
| 구분 | 고정독립변수 (Fixed-X) | 확률독립변수 (Random-X) |
|---|---|---|
| 독립변수 성격 | 연구자가 고정한 값 (설계행렬) | 모집단에서 무작위로 추출된 확률변수 |
| 확률모델 | 조건부 모델: $$ \mathbf{y}\mid \mathbf{X} \sim N(\mathbf{X}\boldsymbol{\beta}, \sigma^2 I) $$ | 결합 모델: $$ f(\mathbf{y}, \mathbf{X}) = f(\mathbf{y}\mid \mathbf{X}) f(\mathbf{X}) $$ |
| 대표 상황 | 실험설계 (농업, 임상시험) | 관측연구 (경제학, 유전학, 사회과학) |
| 추정량 성격 | 조건부 추정량 (주어진 $\mathbf{X}$에 대한 최적해) | 무조건부 추정량 ($\mathbf{X}$의 분포까지 반영) |
| 분산 추정 | 오직 오차항의 분산만 고려 | $\mathbf{X}$ 분포까지 반영 → 더 현실적인 분산 추정 |
| 예측 | 현재 $\mathbf{X}$ 값에 국한된 조건부 예측 | 새로운 표본 $\mathbf{X}$까지 고려한 일반화 예측 가능 |
| 예측구간 | 조건부 예측구간 | 무조건부 예측구간 ($\mathbf{X}$ 분포 반영) |
단순선형회귀에서 고정 독립변수는 실험자가 직접 설정한 값으로, 같은 위치에 점이 고정되고 반응변수 $Y$의 분산만 관찰됩니다. 반면 확률 독립변수는 분포(예: 정규분포)에 따라 달라지므로 $X$ 자체도 흩어져 나타나고, $X$와 $Y$의 공분산 구조가 타원 형태로 시각화됩니다. 이로써 회귀선은 단순히 $Y$의 분산을 설명하는 것에서 벗어나 $X$와 $Y$의 공동 변동성을 반영하게 됩니다.
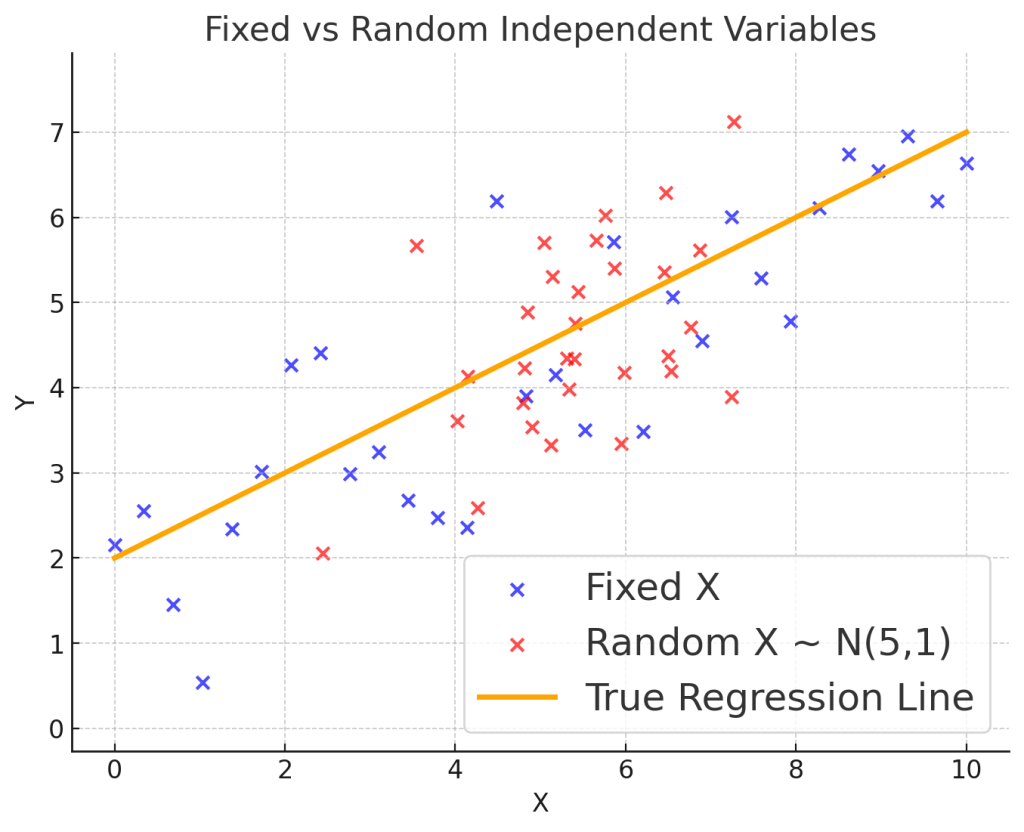
Fig. 1. 단순선형회귀에서 고정독립변수와 확률독립변수의 비교
다중회귀(Multiple Regression)는 하나의 종속변수 $Y$를 두 개 이상의 독립변수 $X_1, X_2, \dots$ 로 설명하는 모델입니다. 독립변수가 2개일 때의 수식은 다음과 같습니다.
$$Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \epsilon_i$$
여기서, $\beta_0$는 절편
$\beta_1$과 $\beta_2$는 각각 $X_1$과 $X_2$의 효과(회귀계수)
$\epsilon_i$는 오차항
이 모델의 해석은 다음과 같습니다.
$\beta_1$: $X_2$가 일정할 때 $X_1$이 1 단위 증가할 때 $Y$의 평균 변화량
$\beta_2$: $X_1$이 일정할 때 $X_2$가 1 단위 증가할 때 $Y$의 평균 변화량
시각적으로는 $X_1, X_2$를 두 축으로, $Y$를 세 번째 축으로 두면 데이터가 3차원 공간에 분포하며, 회귀식은 이 공간에서 하나의 평면(회귀평면)으로 나타납니다.
데이터와 모델
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon},
\qquad
\boldsymbol{\epsilon}\sim \mathcal{N}(\mathbf{0},\,\sigma^2\mathbf{I}_n)
\]
\[
\mathbf{X}=\begin{bmatrix}
1 & X_{11} & X_{12}\\
\vdots & \vdots & \vdots\\
1 & X_{n1} & X_{n2}
\end{bmatrix},\quad
\boldsymbol{\beta}=\begin{bmatrix}\beta_0\\ \beta_1\\ \beta_2\end{bmatrix},\quad
\mathbf{y}=\begin{bmatrix}Y_1\\ \vdots\\ Y_n\end{bmatrix}
\]
반응변수와 오차벡의 공분산
\[
\operatorname{Var}(\boldsymbol{\epsilon})=\sigma^2\mathbf{I}_n,\qquad
\operatorname{Var}(\mathbf{y})=\sigma^2\mathbf{I}_n
\]
OLS 추정량과 그 분산-공분산행렬
\[
\hat{\boldsymbol{\beta}}=(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y},
\qquad
\operatorname{Var}(\hat{\boldsymbol{\beta}})
=\sigma^2(\mathbf{X}^\top\mathbf{X})^{-1}
\]
2개 설명변수의 경우 독립변수행렬곱의 구성
\[
\mathbf{X}^\top\mathbf{X}=
\begin{bmatrix}
n & \sum_i X_{i1} & \sum_i X_{i2}\\
\sum_i X_{i1} & \sum_i X_{i1}^2 & \sum_i X_{i1}X_{i2}\\
\sum_i X_{i2} & \sum_i X_{i1}X_{i2} & \sum_i X_{i2}^2
\end{bmatrix}
\]
정리하면, 다중선형회귀에서 오차 공분산은 $\sigma^2 I_n$, 계수 추정량의 분산–공분산행렬은 $\sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1}$ 입니다.
Fig. 2.은 독립변수 2개를 가진 다중회귀(Multiple Regression)의 시각화입니다. 빨간 점은 실제 관측값이고, 주황색 평면은 추정된 회귀모형을 나타냅니다. 이처럼 두 독립변수 $X_1, X_2$의 결합 효과가 종속변수 $Y$에 선형적으로 영향을 주며, 평면의 기울기와 절편이 회귀계수 $\beta_0, \beta_1, \beta_2$에 해당합니다.
$$\quad \epsilon_i \sim \mathcal{N}(0, \sigma^2)$$
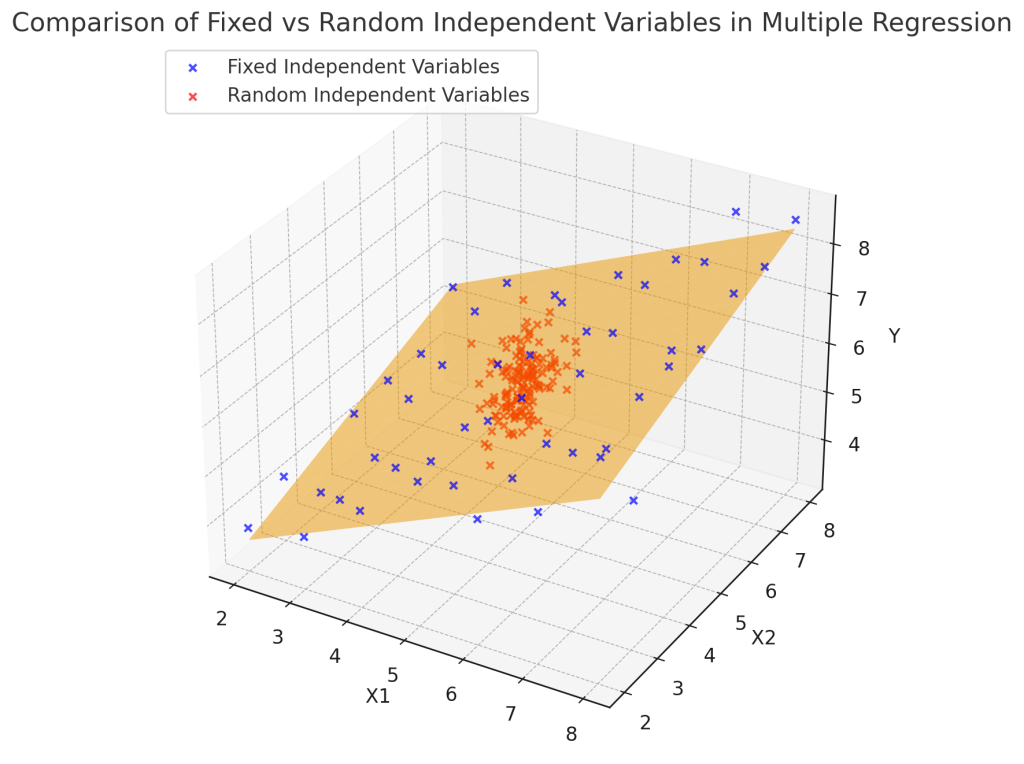
Fig. 2. 다중선형회귀에서 고정독립변수와 확률독립변수의 비교
독립변수 간 공분산 구조가 회귀면의 방향을 결정하는 데 핵심적인 역할을 하며, 상관이 클수록 회귀면 추정은 불안정해집니다. 이를 다중공선성(Multicollinearity) 문제라고 합니다.
1. 회귀계수와 공분산
다중선형회귀에서 추정된 회귀계수 $\hat{\boldsymbol{\beta}}$는 다음식으로 표현됩니다. $\mathbf{X}^\top \mathbf{X}$는 독립변수들의 분산–공분산행렬과 직접 관련됩니다. 즉, 독립변수들의 공분산 구조가 $\hat{\boldsymbol{\beta}}$에 큰 영향을 줍니다.
$$\hat{\beta} = ( \mathbf{X}^\top \mathbf{X} )^{-1} \mathbf{X}^\top \mathbf{y}$$
여기서, $\hat{\beta}$는 최소제곱법(OLS, Ordinary Least Squares)의 정규방정식(normal equation) 해
$\hat{\beta}$는 회귀계수 추정값
$\mathbf{X}$는 설계행렬(design matrix)
$\mathbf{y}$는 반응변수벡터
2. 공분산과 회귀면의 기울기
독립변수들 간에 상관이 없으면 (공분산=0), 각 독립변수는 회귀면의 기울기를 독립적으로 결정합니다. 독립변수들 간에 상관이 크면 (공분산≠0), 회귀계수는 서로 얽혀서 추정되며, 회귀면의 방향이 왜곡됩니다. 즉, 다중공선성 문제가 발생합니다.
3. 타원체와 회귀면 방향
타원체의 긴 축은 독립변수들이 실제로 분산이 큰 방향을 나타내는데, 회귀면도 그 방향에 따라 안정적이거나 불안정하게 추정됩니다. 예를 들어, $X_1$과 $X_2$가 강한 상관을 가지면, 회귀면의 기울기는 한쪽으로 기울어져서 작은 변화에도 민감하게 반응합니다.
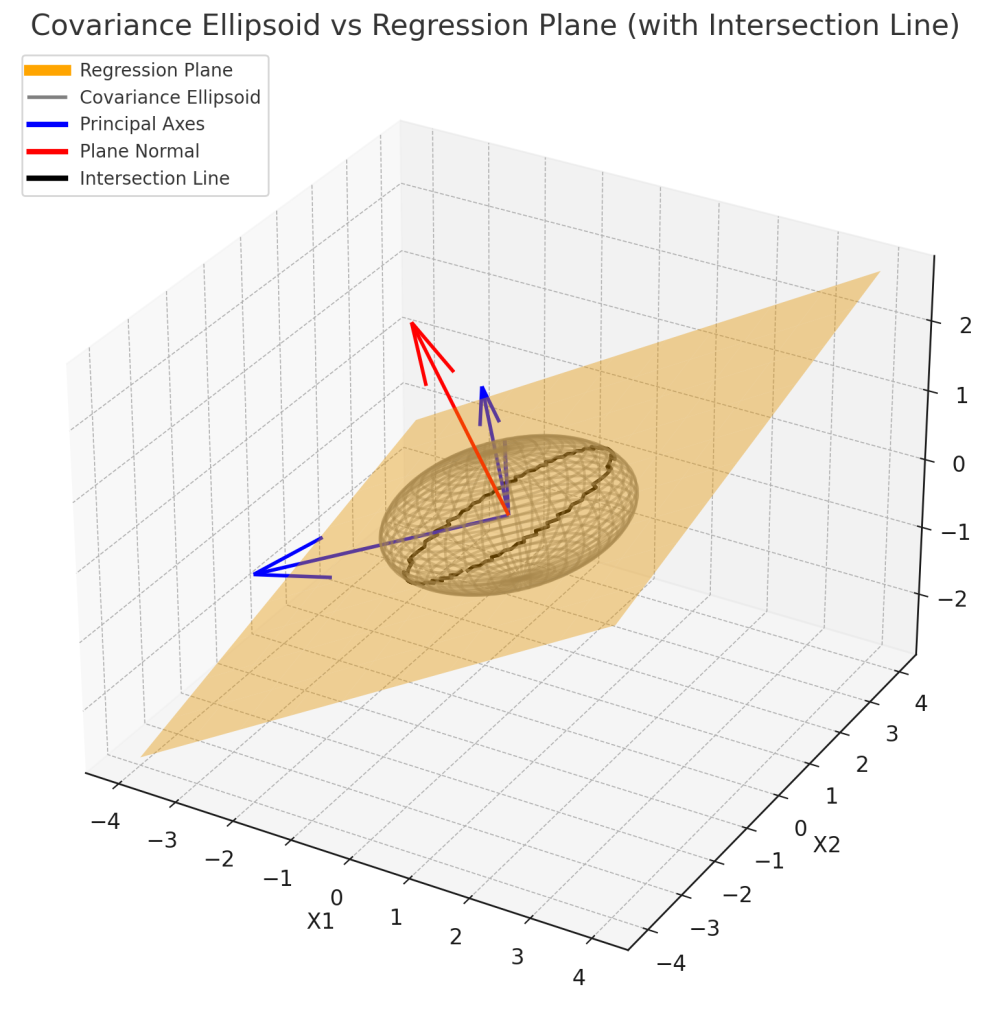
Fig. 2. 다중선형회귀에서 고정독립변수와 확률독립변수의 비교
고정효과 선형모델은 $y = X\boldsymbol{\beta} + \boldsymbol{\epsilon}$ 형태로, 회귀계수 $\boldsymbol{\beta}$ 를 고정된 모수로 두고 추정합니다. 전통적으로는 독립변수 $X$ 를 고정된 값으로 보지만, 이를 모집단에서 추출된 확률변수로 간주하면 결합분포 $f(y,X)$ 에 기반한 분석이 가능해집니다. 이 경우 추정량의 분산은 $X$ 의 분포까지 반영되어 $\sigma^2 , \mathbb{E}[(X^\top X)^{-1}]$ 로 표현되며, 실제 표본 수집 과정과 더 부합하여 예측력과 일반화 가능성을 높이는 장점이 있습니다. 회귀모형은 종속변수 개수와 독립변수 개수에 따라 나뉘는데, 다중 회귀 (Multiple Regression) 는 종속변수 1개와 여러 독립변수, 다변량 회귀 (Multivariate Regression) 는 종속변수 여러 개를 동시에 고려하며, 다변량 다중 회귀 (Multivariate Multiple Regression, MMR) 는 종속변수 여러 개와 독립변수 여러 개가 결합된 가장 일반적인 형태로 반응변수 간 상관구조까지 설명할 수 있습니다.
Table 2. 독립변수가 확률변수인 고정효과 선형모델
| 구분 | 다중 회귀 (Multiple Regression) | 다변량 회귀 (Multivariate Regression) ① 단위가 다른 반응변수 | 다변량 회귀 (Multivariate Regression) ② 단위는 같고 범주만 다른 반응변수 | 다변량 다중 회귀 (Multivariate Multiple Regression, MMR) |
|---|---|---|---|---|
| 종속변수 개수 | 1개 | 여러 개 | 여러 개 | 여러 개 |
| 종속변수 특징 | 단일 변수 | 서로 다른 단위/성격 (예: 키, 몸무게, 혈압) | 단위는 같고 성격은 유사하나 범주가 다름 (예: 수학·영어·과학 점수) | 여러 반응변수 (단위 같거나 다를 수 있음), 동시에 여러 설명변수 고려 |
| 독립변수 개수 | 2개 이상 | 1개 이상 | 1개 이상 | 2개 이상 |
| 확률모델 (첨자 표현) | $$ y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \epsilon_i, \quad \epsilon_i \sim \mathcal{N}(0,\sigma^2) $$ | $$ y_{ij} = \beta_{0j} + \beta_{1j} x_{i1} + \cdots + \beta_{pj} x_{ip} + \epsilon_{ij}, \quad \boldsymbol{\epsilon}_i \sim \mathcal{N}_m(\mathbf{0}, \boldsymbol{\Sigma}) $$ | $$ y_{ij} = \beta_{0j} + \beta_{1j} x_{i1} + \cdots + \beta_{pj} x_{ip} + \epsilon_{ij}, \quad \boldsymbol{\epsilon}_i \sim \mathcal{N}_m(\mathbf{0}, \boldsymbol{\Sigma}) $$ | $$ y_{ij} = \beta_{0j} + \beta_{1j} x_{i1} + \cdots + \beta_{pj} x_{ip} + \epsilon_{ij}, \quad \boldsymbol{\epsilon}_i \sim \mathcal{N}_m(\mathbf{0}, \boldsymbol{\Sigma}) $$ |
| 확률–통계모델 (행렬·벡터 표현) | $$ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \sigma^2 \mathbf{I}_n) $$ | $$ \mathbf{Y} = \mathbf{X}\mathbf{B} + \mathbf{E}, \quad \operatorname{vec}(\mathbf{E}) \sim \mathcal{N}(\mathbf{0}, \mathbf{I}_n \otimes \boldsymbol{\Sigma}) $$ | $$ \mathbf{Y} = \mathbf{X}\mathbf{B} + \mathbf{E}, \quad \operatorname{vec}(\mathbf{E}) \sim \mathcal{N}(\mathbf{0}, \mathbf{I}_n \otimes \boldsymbol{\Sigma}) $$ | $$ \mathbf{Y} = \mathbf{X}\mathbf{B} + \mathbf{E}, \quad \operatorname{vec}(\mathbf{E}) \sim \mathcal{N}(\mathbf{0}, \mathbf{I}_n \otimes \boldsymbol{\Sigma}) $$ |
| \(\boldsymbol{\beta}\) 추정량 | $$ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top \mathbf{y} $$ | $$ \hat{\mathbf{B}} = (\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top \mathbf{Y} $$ | $$ \hat{\mathbf{B}} = (\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top \mathbf{Y} $$ | $$ \hat{\mathbf{B}} = (\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top \mathbf{Y} $$ |
| Random-X 모델 (결합분포 표기) | $$ f(\mathbf{y}, \mathbf{X}) = f(\mathbf{y}\mid \mathbf{X}) f(\mathbf{X}) $$ | $$ f(\mathbf{Y}, \mathbf{X}) = f(\mathbf{Y}\mid \mathbf{X}) f(\mathbf{X}) $$ | $$ f(\mathbf{Y}, \mathbf{X}) = f(\mathbf{Y}\mid \mathbf{X}) f(\mathbf{X}) $$ | $$ f(\mathbf{Y}, \mathbf{X}) = f(\mathbf{Y}\mid \mathbf{X}) f(\mathbf{X}) $$ |
| 대표적 모델 | 단순 다중 회귀 | 일반적 다변량 회귀 | 다반응 회귀 (Multivariate Response Regression), SUR 모형 | MMR, MANOVA |
| 해석 초점 | 하나의 결과를 여러 설명변수로 설명 | 서로 다른 특성을 가진 여러 결과를 동시에 설명 | 같은 척도의 여러 결과를 동시에 설명, 오차 간 상관 구조 강조 | 여러 반응변수와 여러 설명변수 간의 관계를 동시에 설명, 반응변수 간 상관구조 고려 |
| 예시 | 나이·키·운동량으로 몸무게 예측 | 키·몸무게·혈압을 동시에 예측 | 수학·영어·과학 점수를 동시에 예측 | 나이·공부시간·가정환경으로 수학·영어·과학 점수를 동시에 예측 |