아니오. 랜덤효과 ANOVA에서 예측한 집단평균은 표본내 집단평균과 일치하지 않습니다.
고정효과 ANOVA에서는 추정된 집단평균이 표본내에서의 집단평균입니다.
랜덤효과 ANOVA에서는 집단평균 효과는 BLUP(최적 선형 예측치)으로 예측되며, 표본내 집단평균보다 전체평균 쪽으로 수축(shrinkage) 됩니다. 특히 표본 수가 적거나 집단 내 분산이 큰 경우, 표본내 집단평균보다 전체평균에 더 가깝게 조정됩니다.
랜덤효과에서는 예측한 집단평균이 모집단을 반영하므로 표본내에서만의 집단평균과는 차이가 있을 수 밖에 없습니다.
모집단을 반영한 예측과 표본만으로의 추정의 차이라고 볼 수 있습니다.
베이지안은 모수는 확률변수값이며 데이터로 사후분포를 예측(prediction)합니다.
프리퀀티스트는 모수는 상수이며 데이터로 추정(estimation)합니다.
고정효과 ANOVA는 고정효과 선형모델이라고도 부릅니다.
고정효과 ANOVA는 비교하려는 집단이 모두 특정하고 고정되어 있다고 가정하는 분석 방법입니다. 예를 들어, A반, B반, C반처럼 “내가 관심 있는 집단들”을 모집단 대표가 아니라, 그 자체로 분석 대상으로 보는 분산분석방법입니다.
모델식은 다음과 같습니다.
$$Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}$$
여기서, $Y_{ij}$: $i$번째 집단, $j$번째 데이터
$\mu$: 전체 평균 (grand mean)
$\alpha_i$: 집단 $i$의 효과 (상수)
$\varepsilon_{ij}$: 오차항, $\varepsilon_{ij} \sim N(0,\sigma^2)$
추정방법은 각 집단의 평균을 표본평균 그대로 사용합니다. 즉, 집단 효과는 “그 집단 평균 – 전체 평균”으로 정의됩니다. 이는 단순히 산술평균 계산이므로, 추정(estimation)입니다.
$$\hat{\alpha}_i = \bar{Y}_{i\cdot} – \bar{Y}_{\cdot\cdot}$$
검정은 F-검정을 사용하며 집단 간분산과 집단내분산의 양의 비로 비교합니다. 귀무가설은 “집단평균 간에 차이 없다”입니다.
$$H_0 : \alpha_1 = \alpha_2 = \cdots = \alpha_k = 0$$
대립가설은 적어도 “하나의 집단평균은 다르다”입니다.
$H_1$ : 적어도 하나의 집단 평균은 다르다.
고정효과 ANOVA는 선택된 집단 간의 평균 차이만을 검정합니다. “이 집단들 간에는 차이가 있다/없다”를 검정하며 검정결과를 모집단내에 있는 집단으로 일반화할 수는 없습니다.
고정효과 ANOVA는 표본평균 그대로 추정합니다. 가설은 “집단 평균 간 차이가 있는가?”이며 선택된 집단에만 한정된 결론입니다. 고정효과 ANOVA에서는 집단을 모집단내의 집단들의 대표로 보지 않습니다.
랜덤효과 ANOVA는 랜덤효과 선형모델이라고도 부릅니다. 또한 랜덤효과가 하나 있는 선형혼합모형(LMM) 의 특수한 경우입니다. 즉, 랜덤효과 ANOVA는 $\mathbf{X}$가 상수벡터(전체 평균만 포함), $\mathbf{Z}$가 집단 더미행렬인 경우의 LMM 특수형태입니다. 집단효과를 랜덤으로 두는 순간, LMM 구조가 성립합니다.
랜덤효과 ANOVA는 비교하려는 집단이 모집단에서 무작위로 뽑힌 표본 집단이라고 가정하는 분석 방법입니다. 따라서 집단평균을 상수(고정값)가 아니라 확률변수로 모델링합니다. 초점은 “집단 간 차이의 크기”가 아니라 “집단 간 변동성(분산)이 존재하는가”입니다.
모델식은 다음과 같습니다.
$$Y_{ij} = \mu + u_i + \varepsilon_{ij}$$
여기서, $Y_{ij}$는 $i$번째 집단, $j$번째 데이터
$\mu$는 전체 평균 (grand mean)
$u_i$는 집단 $i$의 효과 (랜덤효과, $u_i \sim N(0, \sigma_u^2)$)
$\varepsilon_{ij}$는 오차항, $\varepsilon_{ij} \sim N(0, \sigma_\varepsilon^2)$
추정방법은 분산성분 $\sigma_u^2, \sigma_\varepsilon^2$를 REML(Restricted Maximum Likelihood) 또는 ML(Maximum Likelihood)로 추정합니다. 집단 효과 $u_i$는 상수가 아니라 확률변수이므로, 직접 추정 (estimation)하지 않고 예측(prediction)을 합니다.
예측값은 BLUP (Best Linear Unbiased Prediction)이며 다음식으로 표현합니다.
$$\hat{u}_i = \frac{\sigma_u^2}{\sigma_u^2 + \sigma_\varepsilon^2 / n_i} \left(\bar{Y}_{i\cdot} – \bar{Y}_{\cdot\cdot}\right)$$
여기서, $Y_{ij}$는 $i$번째 집단의 $j$번째 관측값 (데이터, 확률변수)
$\bar{Y}_{i\cdot}$는 $i$번째 집단의 표본평균:
$$\bar{Y}_{i\cdot} = \frac{1}{n_i} \sum_{j=1}^{n_i} Y_{ij}$$
$\bar{Y}_{\cdot\cdot}$ 전체 표본평균 (grand mean):
$$\bar{Y}_{\cdot\cdot} = \frac{1}{\sum_i n_i} \sum_i \sum_{j=1}^{n_i} Y_{ij}$$
$\mu$는 모집단 전체의 평균 (고정효과, 모수)
$u_i$는 $i$번째 집단의 랜덤효과:
$$u_i \sim N(0, \sigma_u^2)$$
$\varepsilon_{ij}$는 오차항:
$$\varepsilon_{ij} \sim N(0, \sigma_\varepsilon^2)$$
Shrinkage 계수는 다음식으로 정의합니다.
$$\lambda_i = \frac{\sigma_u^2}{\sigma_u^2 + \sigma_\varepsilon^2 / n_i}$$
여기서, $\lambda_i$는 집단 평균을 얼마나 그대로 반영할지를 정하는 가중치: $0 \leq \lambda_i \leq 1$
$\lambda_i$가 1에 가까우면 집단 평균 $\bar{Y}_{i\cdot}$를 거의 그대로 사용합니다. $\lambda_i$가 0에 가까우면 전체 평균 $\bar{Y}_{\cdot\cdot}$ 쪽으로 강하게 수축(shrinkage)합니다.
집단내분산 $\sigma_\varepsilon^2$가 크거나, 표본 크기 $n_i$가 작으면 $\lambda_i$는 작아지고 집단평균을 신뢰하지 못하므로 전체평균 쪽으로 보정합니다. 집단간분산 $\sigma_u^2$가 크거나, 표본 크기 $n_i$가 충분히 크면 $\lambda_i$는 커지고 집단평균을 그대로 반영합니다.
검정은 랜덤효과 ANOVA는 “이 집단들 간에 차이가 있는가?”보다 “모집단에서 집단 간 변동성이 존재하는가?”를 묻는 분석입니다. 따라서 검정결과는 표본 집단에 국한되지 않고, 모집단 전체로 일반화할 수 있습니다.
귀무가설은 “집단간분산이 없다” 또는 “집단차이가 없다”입니다.
$$H_0 : \sigma_u^2 = 0$$
대립가설은 “집단간분산이 존재한다”입니다.
$$H_1 : \sigma_u^2 > 0$$
“회귀(regression)”라는 말은 엄밀히 랜덤효과 ANOVA모델에서 더 자연스럽게 드러난다고 할 수 있습니다. 회귀(= 평균으로 수축·회귀)라는 현상은 랜덤효과 ANOVA에서만 발생합니다. 고정효과 ANOVA는 회귀가 아니라 단순히 “차이 추정”일 뿐입니다.
Table 1. 고정효과 ANOVA와 랜덤효과 ANOVA 비교
| 구분 | 고정효과 (Fixed Effects ANOVA) | 랜덤효과 (Random Effects ANOVA) |
|---|---|---|
| 모형식 | $Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}$, $\alpha_i$는 상수 | $Y_{ij} = \mu + u_i + \varepsilon_{ij},\; u_i \sim N(0,\sigma_u^2)$ |
| 집단 효과 의미 | 선택된 특정 집단의 평균 차이를 직접 추정 | 모집단에서 무작위로 뽑힌 집단 평균의 편차 (확률변수) |
| 전체 평균 $\mu$ | $\hat{\mu} = \bar{Y}_{\cdot\cdot}$ (전체 표본평균) | 동일하게 $\hat{\mu} = \bar{Y}_{\cdot\cdot}$ |
| 집단 효과 추정 | $\hat{\alpha}_i = \bar{Y}_{i\cdot} – \bar{Y}_{\cdot\cdot}$ (집단평균 – 전체평균) | $\hat{u}_i$ = BLUP (최적 선형 예측치), 분산성분 $\sigma_u^2, \sigma_\varepsilon^2$은 REML/ML로 추정 |
| 검정의 초점 | 집단 평균 간 차이가 있는가? ($\alpha_i$ 유의성) | 집단 간 분산이 유의한가? ($\sigma_u^2 > 0$) |
| 일반화 가능성 | 선택된 집단에 한정된 결론 | 모집단 전체로 일반화 가능 |
| 예시 | 특정 3개 학급 성적 평균 비교 | 수많은 학급 중 무작위 샘플 학급 성적 분산 추정 |
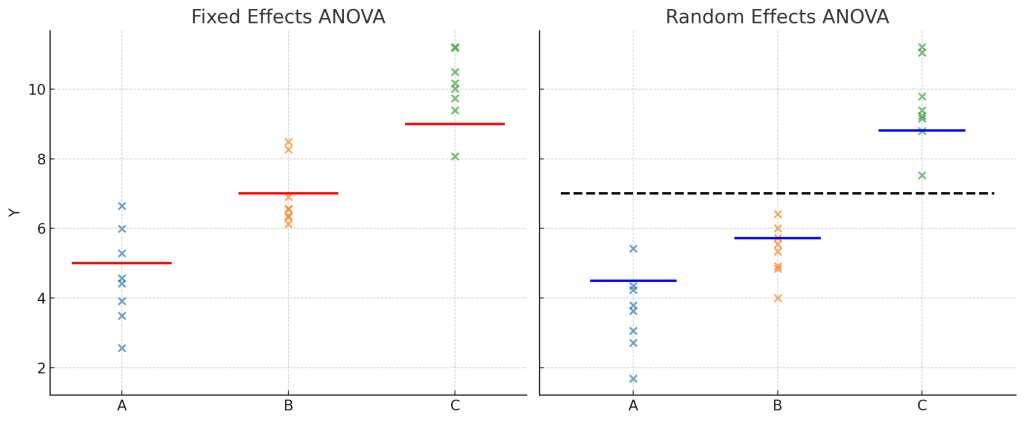
Fig. 1. 고정효과 ANOVA와 랜덤효과 ANOVA 비교