정수, 유리수, 무리수, 실수 중에서 연속인 수체계는?
목차 실수입니다. 연속성의 필요성: 연속성이 보장된 실수 함수 위에서만 미분과 적분이 성립됩니다. 시간, 거리, 온도 등의 연속적인 양은 실수로 표현되어야 합니다. 극값을 정의하고 분석하기 위해서는 함수가 연속적이어야 하며, 이러한 연속성은 실수 공간에서 보장됩니다. 1. 수체계 수체계(Number System)는 수학적 연산과 논리 체계 내에서 수의 집합들을 공리적으로 정의하고, 그 위상 및 대수적 구조에 따라 분류한 계층적 구조입니다. […]
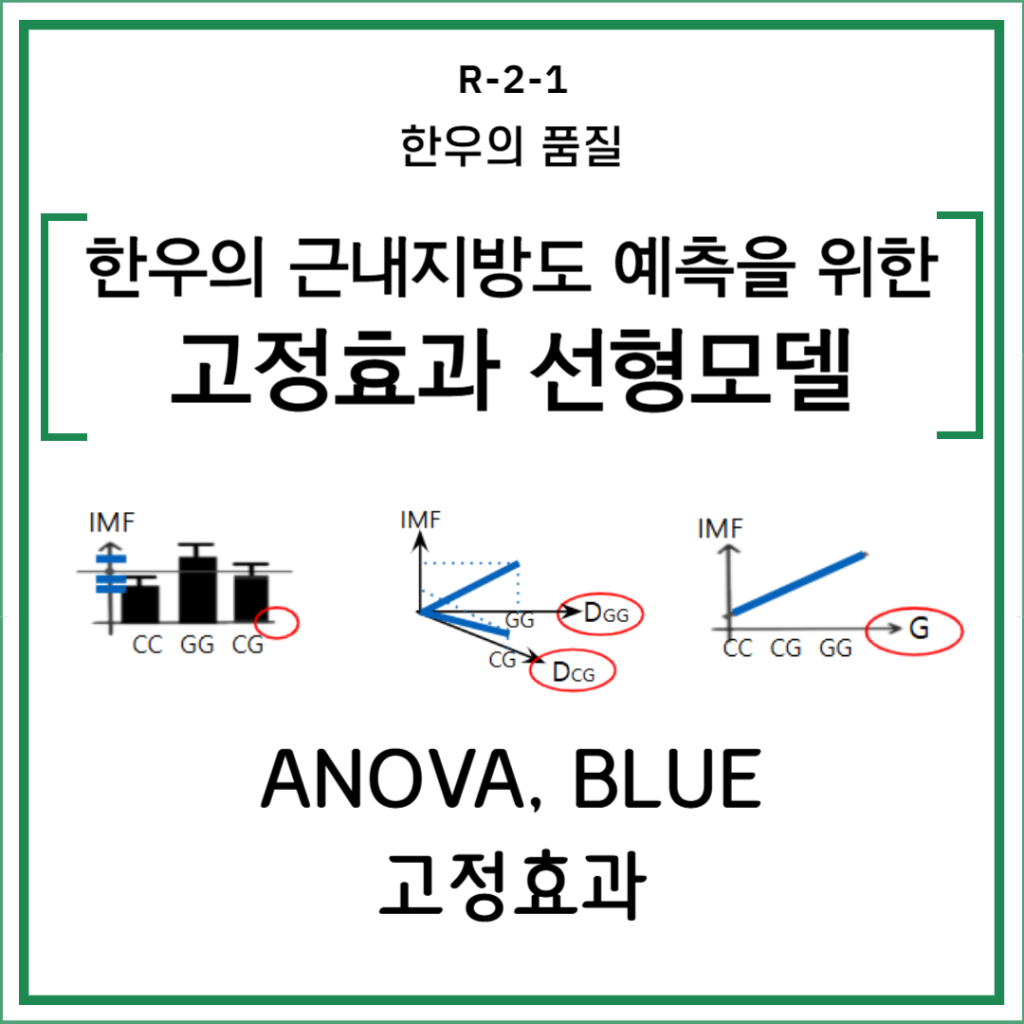
선형모형을 이용한 SNP 마커 효과 분석: ANOVA 모형을 이용한 마커의 평균 효과 추정
목차 요약영상 1 Videos 모델링 3:54 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 프로그램 데이터 모델링 데이터분석 논문작성 연구계획 데이터셋, 통계량, 시각화 확률모델 확률분포 새확률변수 통계모델 집단비교 상관분석 t검정 질문-가설 데이터 프레임 범주형 확률변수1 범주형 확률변수2 교차된 범주형 확률변수 확률분포 주변확률분포 결합확률분포 새확률변수, 통계량 통계량 확률분포 귀무가설 검정통계량 검정통계량 확률분포 유의확률과 유의수준으로 검정 […]
반응표면방법론
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 반응표면방법론(Response Surface Methodology, RSM) 반응표면방법론(Response Surface Methodology, RSM)은 실험설계 및 분석 기법 중 하나로, 여러 개의 독립변수가 종속변수에 미치는 영향을 조사하고 최적화하는 방법입니다. 반응표면방법론은 일반적으로 실험계획법(Design of Experiments, DOE)을 기반으로 하며, 종속변수의 값과 독립변수들의 […]
다항회귀모델
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 다항회귀모형 회귀모형에서 회귀식이 원인변수(설명변수)들의 다항식으로 표시 되는 경우 이를 다항회귀모형(polynomial regression model) 이라 한다. 예를 들어, 단순선형회귀모형은 설명변수가 하나 있는 일차(first-order) 다항회귀모형으로 볼 수 있고, 다음은 이차(second-order) 다항회귀모형들의 예이다. 원인변수(설명변수)가 1개 : 2차 […]
경사하강법과 최대경사법
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 경사하강법(Gradient descent) 경사하강법(Gradient descent)은 컴퓨터를 이용해 함수의 최소값을 찾는 방법 중 널리 쓰이는 방법입니다. 주된 원리는 내려가는 방향을 정할 때 그 점에서의 기울기(미분계수값)가 가장 작은 방향으로 계속해서 선택하는 나가는 것입니다. 방향과 함께 Step의 […]
정규분포를 따르는 확률변수의 벡터가 생성하는 표현공간에서의 결합확률분포는 무엇?
목차 다변량 정규분포(multivariate normal distribution)입니다. 변량은 확률변수의 실제 관측값을 의미합니다. 어떤 확률공간 $(Omega, mathcal{F}, P)$ 위에 정의된 정규분포 확률변수 벡터 $ mathbf{X} = (X_1, ldots, X_n)^top $가 있을 때, 그 벡터가 표현공간 $ mathbb{R}^n $에서 따르는 결합확률분포 $ P_{mathbf{X}} $는 다변량 정규분포 $mathcal{N}(boldsymbol{mu}, boldsymbol{Sigma})$입니다. 확률변수는 항상 어떤 확률공간 ($Omega$, $mathcal{F}$, $P$) 상에 정의됩니다. 정규분포를 나타내는 […]
최대가능도법 Maximum Likelihood Method
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 곱사건 (joint event) : $Acap B$, $Bcap A$ 1.1. 독립된 두 사건의 곱사건 : 교환법칙 성립 A사건과 B사건이 서로 독립이라는 것은 A사건의 결과와 B사건의 결과가 서로 영향을 주지 않음을 의미합니다. A사건과 B사건이 독립이면 […]
다변량 정규분포는 여러 개의 정규분포를 합친 것인가?
목차 아니요, 변량(확률변수값) 간의 상관이 있어야 합니다. 다변량 정규분포는 정규성과 상관이 있는 확률변수들을 원소로 하는 벡터의 확률분포입니다. 개체의 속성이 정규분포를 나타내고 개체의 속성이 서로 상관을 가질 때 개체가 이루는 집단의 속성의 분포는 확률변수 벡터로 표현되며 그 벡터는 다변량 정규분포를 나타냅니다. 다변량 정규분포를 나타내는 대표적인 확률변수 벡터로는 집단의 육종가 벡터가 있습니다. [mathbf{a} = begin{pmatrix}a_1 \a_2 \vdots […]
BLUE (Best Linear Unbiased Estimator)
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. BLUE BLUE는 Best Linear Unbiased Estimator의 첫글자로 만든 조어입니다. 번역하면 “최선의 선형불편추정량”입니다. 말그대로 추정방법 중 하나입니다. 여기서 최선(best)의 추정량은 집단의 분산이 가장 작을 때, 모수의 추정량이라는 것을 의미합니다. 선형(Linear)이라 함은 모수의 추정량 식에서 […]
최소제곱법 Least Square Method
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. BLUE에서의 최소제곱법 단순선형회귀모형 $$f(x)=beta_{0}+beta_{1}x$$ 단순선형회귀 관측모형 $$y_{i}=beta_{0}+beta_{1}x_{i}+epsilon_{i}$$ 잔차제곱합 $$sum_{i=1}^{n}epsilon_{i}^2$$ 잔차제곱합의 최소 $$OLS=Minleft(lim_{i=1}^{n}(y_{i}-beta_{0}-beta_{1}x_{i})^2right)$$ 2. 최소제곱법으로 회귀계수를 구하는 계산법 중 해석학적(Algebraic)방법 $$hat{beta}_0=overline{Y}-hat{beta}_1overline{X}$$ $$hat{beta}_1=dfrac{sumlimits_{i=1}^{n}(X_i -overline{X})(Y_i -overline{Y})}{sumlimits_{i=1}^{n}(X_i -overline{X})^2}$$ $$sum_{i=1}^{n}|varepsilon_i|=sum_{i=1}^{n}|Y_i -beta_0-beta_1 X_i|$$ $$hat{beta}_1=rdfrac{s_y}{s_x}$$ $$dfrac{hat{y}_i -overline{y}}{s_y}=rdfrac{x_i -overline{x}}{s_x}$$ 3. 최소제곱법으로 […]

