문항반응척도
애니메이션 그림 데이터 종류 데이터 수집 데이터 종류 데이터 종류 데이터 수집 데이터 종류 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 문항반응척도의 유형 문항반응에서는 응답자가 문항에 반응한 결과가 결과변수가 되는 경우와 응답자의 능력과 문항의 난이도가 반응하여 결과가 나오는 경우가 있습니다. 전자의 원인변수는 […]
당도 척도
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 당도(糖度, sweetness) 당도는 음식이나 음료에 포함된 설탕의 양을 나타내는 “척도”입니다. 이는 주로 과일, 채소, 주스, 소스, 와인 등에 포함된 자연적 또는 첨가된 설탕의 농도를 측정하는 데 사용됩니다. 당도는 음식이나 음료의 맛에 큰 영향을 […]
척도와 측도
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. “0”의 의미 척도의 의미를 이해하는데 있어, 척도에서 사용한 “0”에 대한 이해가 선행되어야 합니다. 1.1. 실체의 부재 실체를 정의하고, 그 실체가 없음을 나타낼 때, 0을 사용합니다. 예를 들어, 사과가 0개 있다는 의미는 사과가 무엇인지 […]
정규분포는 표본의 평균과 분산이 독립인 유일한 확률분포인가요?
목차 네, 정규분포의 표본평균과 표본분산은 확률변수이고 독립입니다. 정규분포 $mathcal{N}(mu, sigma^2)$ 에서 추출된 모든 $n geq 2$의 표본에서 표본평균($ bar{X}$)과 표본분산$(S^2)$은 독립입니다. $$bar{X} perp S^2$$ 표본의 평균과 분산이 독립이라는 것은 어느 표본의 평균값을 알아도 분산값을 예측할 수 없고 반대도 마찬가지라는 것입니다. 1. 정규분포 정규분포 $X sim mathcal{N}(mu, sigma^2)$의 확률밀도함수는 다음식으로 표현됩니다.$$f(x) = frac{1}{sqrt{2pi sigma^2}} expleft( -frac{(x […]
ssGBLUP

데이터 시뮬레이션 데이터셋 관측 데이터셋 모수 가설검정 대응표본 t검정 독립표본 t검정 일원분산분석 F검정 상관분석 t검정 단순선형회귀분석 F검정 단순선형회귀분석 t검정 비모수 가설검정 교차분석 카이제곱검정 연관분석 카이제곱검정 선형모델 구축 BLUE 데이터 범주형 변수로 개체의 범주형 속성을 표현 범주형 변수는 변수값(관측값)이 범주(category)를 나타내는 값. 개체가 속하는 카테고리는 범주형 변수의 변수값으로 표현, 예를 들어, 인간이라는 범주형 변수에 남자와 여자라는 […]
GBLUP

데이터 시뮬레이션 데이터셋 관측 데이터셋 모수 가설검정 대응표본 t검정 독립표본 t검정 일원분산분석 F검정 상관분석 t검정 단순선형회귀분석 F검정 단순선형회귀분석 t검정 비모수 가설검정 교차분석 카이제곱검정 연관분석 카이제곱검정 선형모델 구축 BLUE 데이터 범주형 변수로 개체의 범주형 속성을 표현 범주형 변수는 변수값(관측값)이 범주(category)를 나타내는 값. 개체가 속하는 카테고리는 범주형 변수의 변수값으로 표현, 예를 들어, 인간이라는 범주형 변수에 남자와 여자라는 […]
PBLUP

데이터 시뮬레이션 데이터셋 관측 데이터셋 모수 가설검정 대응표본 t검정 독립표본 t검정 일원분산분석 F검정 상관분석 t검정 단순선형회귀분석 F검정 단순선형회귀분석 t검정 비모수 가설검정 교차분석 카이제곱검정 연관분석 카이제곱검정 선형모델 구축 BLUE 데이터 범주형 변수로 개체의 범주형 속성을 표현 범주형 변수는 변수값(관측값)이 범주(category)를 나타내는 값. 개체가 속하는 카테고리는 범주형 변수의 변수값으로 표현, 예를 들어, 인간이라는 범주형 변수에 남자와 여자라는 […]
BLUE
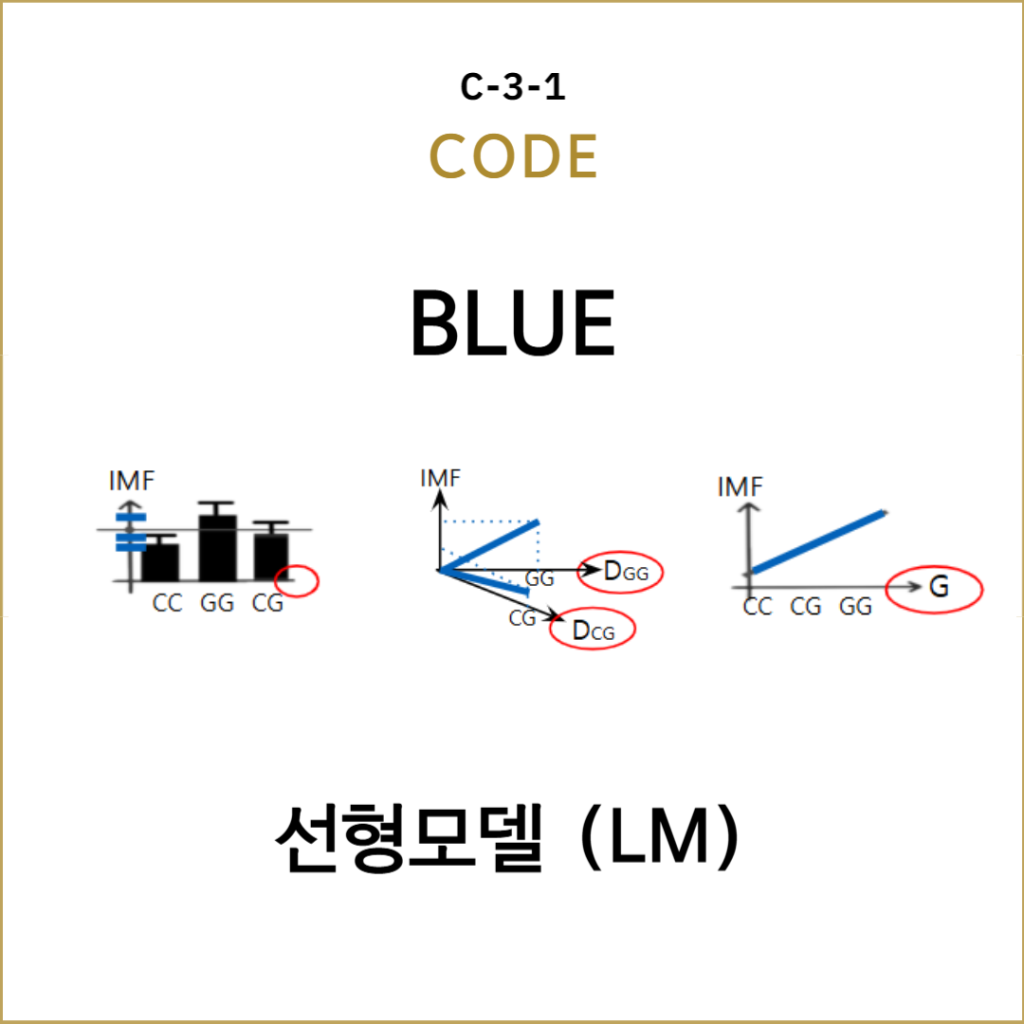
데이터 시뮬레이션 데이터셋 관측 데이터셋 모수 가설검정 대응표본 t검정 독립표본 t검정 일원분산분석 F검정 상관분석 t검정 단순선형회귀분석 F검정 단순선형회귀분석 t검정 비모수 가설검정 교차분석 카이제곱검정 연관분석 카이제곱검정 선형모델 구축 BLUE 데이터 범주형 변수로 개체의 범주형 속성을 표현 범주형 변수는 변수값(관측값)이 범주(category)를 나타내는 값. 개체가 속하는 카테고리는 범주형 변수의 변수값으로 표현, 예를 들어, 인간이라는 범주형 변수에 남자와 여자라는 […]
상대도수는 모비율 추정량의 실현값인가?
목차 네. 상대도수(relative frequency)는 모비율 추정량의 실현값입니다. $$hat{p}_{mathrm{obs}} = dfrac{x}{n}$$ 여기서, $hat{p}_{mathrm{obs}}$은 관측된 표본의 상대도수 $x$는 실현된 성공회수 $n$은 표본크기 모비율은 특정 사건이 일어나는 데 성공하는 비율이며 알 수 없는 상수입니다. $$pi = P(text{특정사건})$$ 모비율 추정량은 표본비율(sample proportion)이며 분포를 가지는 확률변수입니다. $$hat{p} = dfrac{X}{n}, quad X sim mathrm{Binomial}(n, pi)$$ 여기서, $hat{p}$은 모비율 추정량 1. […]
자연상수
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1. 복제(複製)와 자연상수 은행A는 합의한 예치기한 후에 예금액에 더해 예금액과 같은 금액의 이자를 주는 은행입니다. 다르게 표현하면, 예금자와 합의한 기간 동안 입금액을 복제해 주는 은행입니다. $$Y=I+Idfrac{T}{T}=2I$$ 여기서 $Y$는 출금액 $I$는 예금액(입금액) $T$는 합의한 기간 예를 […]

