a의 자연로그를 증가율로 하는 지수함수입니다.
$$a^x=\left(e^{\ln(a)}\right)^x=e^{x\ln(a)}$$
여기서, $\ln(a)$는 증가율(growth rate)
어떤 양의 실수 $a$에 대해서도 지수함수 $a^x$는 $e$를 밑으로 하는 지수함수 $e^{x\ln(a)}$로 나타낼 수 있습니다.
Table1. 지수함수의 밑 a의 구간에 따른 지수함수의 성질
| 밑 a의 구간 | ln(a)의 부호 | 지수형태 표현 | 도함수 및 적분함수 | 지수함수 성질 |
|---|---|---|---|---|
| \( 0 < a < 1 \) | \( \ln a < 0 \) | \( e^{x \cdot \ln a} \) | 도함수: \( a^x \ln a \) 적분함수: \( \dfrac{a^x}{\ln a} + C \) | 감소 지수함수 \( x \to \infty \)일 때 \( 0 \)에 수렴 |
| \( a = 1 \) | \( \ln 1 = 0 \) | \( e^{x \cdot 0} = 1 \) | 도함수: \( 0 \) 적분함수: \( x + C \) | 상수함수 모든 \( x \)에서 값이 \( 1 \) |
| \( a = e \) | \( \ln e = 1 \) | \( e^x \) | 도함수: \( e^x \) 적분함수: \( e^x + C \) | 증가 지수함수 도함수와 적분함수가 자기 자신 자연로그 함수 \( \ln x \)의 역함수 |
| \( 1 < a < e \) 또는 \( a > e \) | \( \ln a > 0 \) | \( e^{x \cdot \ln a} \) | 도함수: \( a^x \ln a \) 적분함수: \( \dfrac{a^x}{\ln a} + C \) | 증가 지수함수 \( x \to \infty \)일 때 발산 |
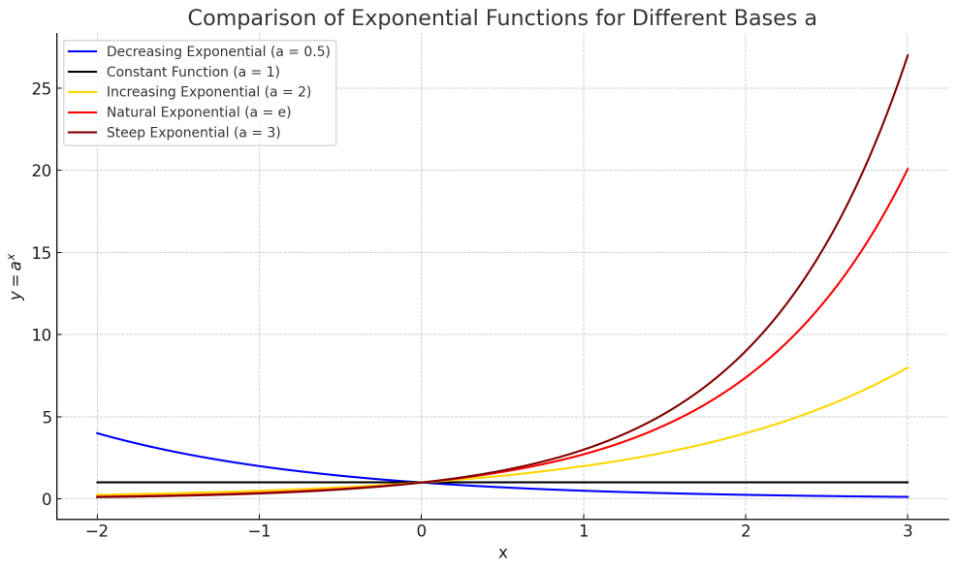
Fig.1 양의 실수인 밑 a에 따른 지수함수 그래프
자연계에서 일어나는 확률적 현상을 다음식으로 표현할 수 있습니다.
$$f(x) \propto e^{-g(x)}$$
여기서, $g(x)$는 양의 함수: 함수값이 클 수록 확률은 작아짐.
예를 들어 정규분포에서는 중심에서 멀어질수록 확률이 급격히 작아집니다.
양의 함수 $g(x)$는 에너지, 손실, 거리, 비용일 수 있습니다.
Table 2. 지수함수의 적용과 지수에 있는 함수의 의미
| 적용 | 함수 $g(x)$의 의미 |
|---|---|
| 정규분포 | 오차 제곱: \( (x – \mu)^2 \) (중심에서 벗어난 정도) |
| 볼츠만 분포 | 에너지 \( E(x) \) |
| 최적화 기반 모델 | 손실 함수, 비용 함수 \( L(x) \) |
| 베이지안 추론 | 로그 우도 함수 \( -\log p(x) \) |
| 기계학습 모델 | 손실 함수 또는 negative log-likelihood |
Table 3. 지수함수 기반 확률분포 비교표
| 확률분포 | 확률밀도함수 (PDF) | 정의역 | 주요 활용 분야 |
|---|---|---|---|
| 지수분포 | $$f(x) = \lambda e^{-\lambda x}$$ | $$x \ge 0$$ | 포아송 과정의 대기 시간 모델링 |
| 정규분포 | $$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \, e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$ | $$x \in \mathbb{R}$$ | 자연 현상, 측정 오차 |
| 감마분포 | $$f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha – 1} e^{-\beta x}$$ | $$x > 0$$ | 대기 시간, 신뢰성 분석 |
| 라플라스분포 | $$f(x) = \frac{1}{2b} e^{-\frac{|x – \mu|}{b}}$$ | $$x \in \mathbb{R}$$ | 강건 통계, 신호 처리 |
| 볼츠만(기브스) 분포 | $$P(x) \propto e^{-E(x)/kT}$$ | $$x \in \mathbb{R} \text{ (상태공간)}$$ | 통계역학, 에너지 분포 |
| 로지스틱 분포 | $$f(x) = \frac{e^{-(x-\mu)/s}}{s(1 + e^{-(x-\mu)/s})^2}$$ | $$x \in \mathbb{R}$$ | 로지스틱 회귀, 분류 모델 |
지수에 허수가 들어가는 경우를 복소 지수함수라고 합니다. 복소 지수함수는 삼각함수와의 연결 고리이며 실수 함수와 달리 회전을 표현합니다.푸리에 해석, 파동방정식, 양자역학에서 사용됩니다. 복소 지수함수 $e^{ix}$는 실수 $x$에 대한 복소수 값을 반환하는 함수입니다.
$$e^{ix} = \cos x + i \sin x$$
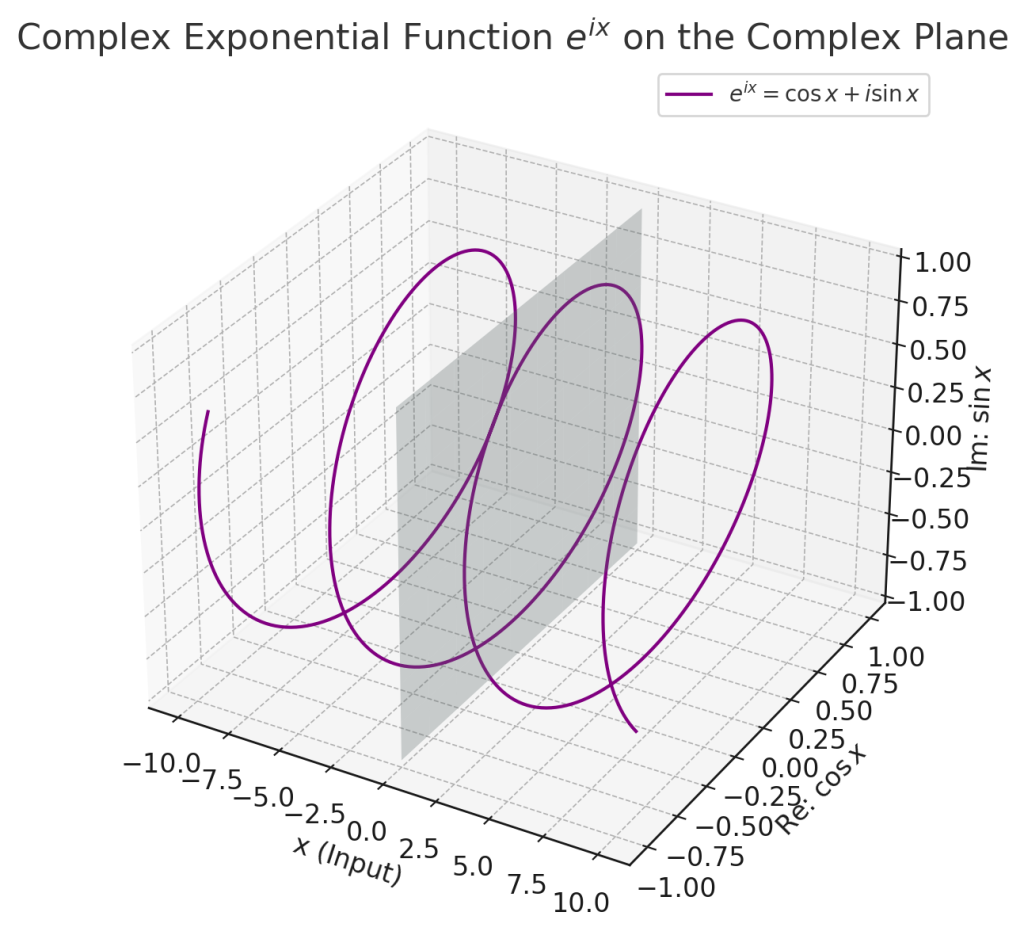
Fig. 2. 입력 실수 $x$에 따른 허수를 지수로 하는 함수값의 궤적
지수에 행렬이 들어가는 경우를 행렬지수 함수라고 합니다. $e^A$는 $A$에 대한 함수이며 행렬을 입력받아 행렬을 출력하는 함수입니다.
행렬의 지수함수 (matrix exponential)는 테일러 급수로 정의됩니다.
$$e^{A} = \sum_{n=0}^{\infty} \frac{A^n}{n!}$$
여기서, $A$는 행렬
예를 들어 선형미분방정식의 해에서 사용됩니다.
$$\frac{d\mathbf{x}}{dt} = A \mathbf{x}
\quad \Rightarrow \quad
\mathbf{x}(t) = e^{At} \mathbf{x}(0)$$
이 때 행렬 A가 다음과 같으면
$$A = \begin{bmatrix}
0 & -1 \\
1 & 0.5
\end{bmatrix}$$
복소 고유값은 다음과 같이 계산됩니다.
$$\lambda = \frac{0.5 \pm \sqrt{-3}}{2} = 0.25 \pm 0.866i$$
이 때 $\mathbb{x}(t)$는 나선형회전과 지수적 팽창(또는 수축)을 합니다.
$$e^{At} = \sum_{n=0}^{\infty} \frac{(At)^n}{n!}$$
$$\mathbf{x}(t) = e^{At} \, \mathbf{x}_0 =e^{At} \cdot
\begin{bmatrix}
x_1(0) \\
x_2(0)
\end{bmatrix}$$
여기서, $\mathbf{x}(t)$는 시간에 따라 변하는 2차원벡터
$A$는 시스템의 선형변환행렬
$e^{At}$는 행렬지수함수
시작점이 다음과 같을 때 그래프는 Fig. 2 와 같습니다.
$$\mathbf{x}_0 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}
$$
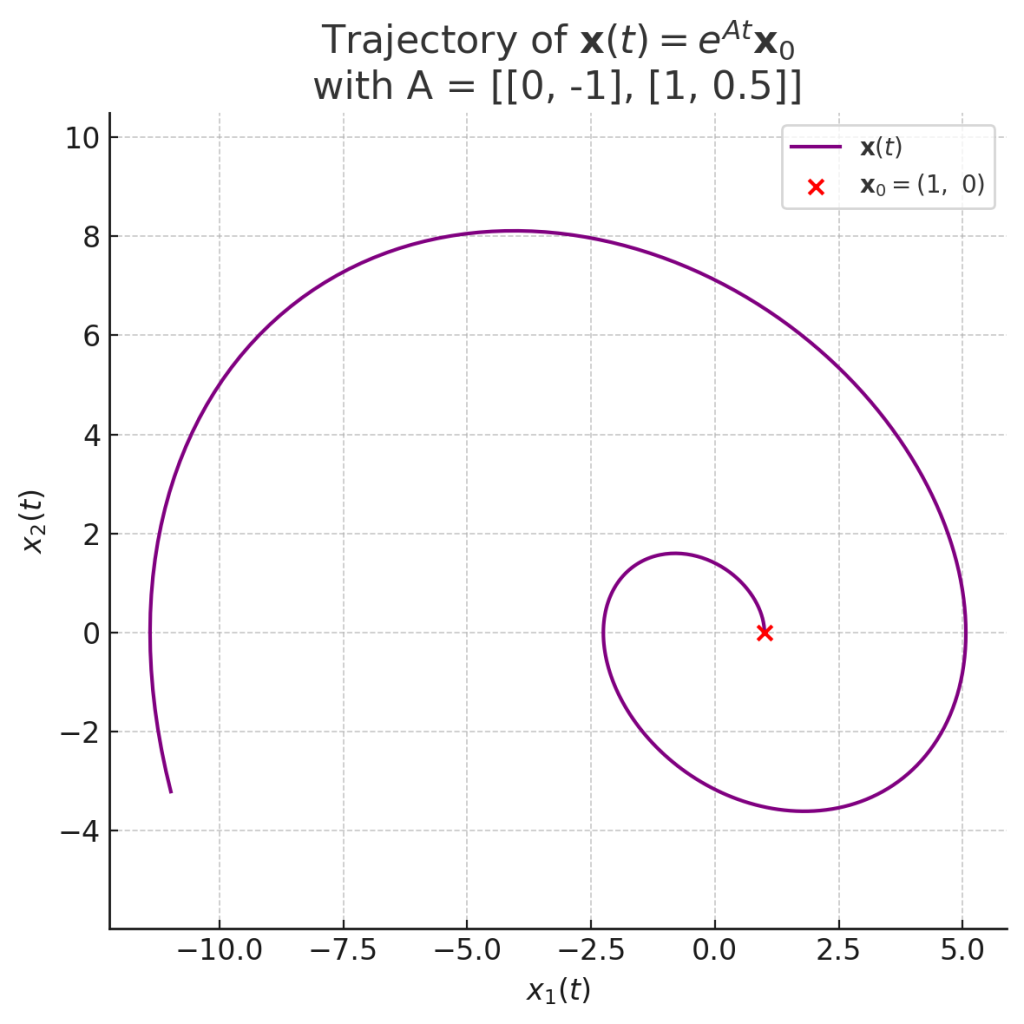
Fig.3. $\mathbb{x}_0$을 시작점하고 상태행렬 $A$에 의한 $t$에 따른 $\mathbb{x}(t)$의 궤적
지수함수의 지수에 어떤 수체계가 들어가는 가에 따라 여러가지 함수가 만들어 집니다.
$$\begin{aligned}
&\text{실수 지수:} && e^{x} \\
&\text{복소 지수:} && e^{ix} \\
&\text{행렬 지수:} && e^{A} = \sum_{n=0}^{\infty} \frac{A^n}{n!} \\
&\text{시간에 따라 변하는 행렬:} && e^{M(x)} \\
\end{aligned}$$
Table 4. 지수함수 표현 비교표
| 구분 | 표현 | 정의역 | 치역 | 의미 | 사용 분야 |
|---|---|---|---|---|---|
| 실수 지수 | $$e^x$$ | $$x \in \mathbb{R}$$ | $$\mathbb{R}^+$$ | 실수 \(x\)에 대한 지수함수 | 일반 함수, 통계분포, 경제모형 등 |
| 복소 지수 | $$e^{ix}$$ | $$x \in \mathbb{R}$$ | $$\mathbb{C}$$ (단위원) | 회전 표현 (오일러 공식) | 푸리에 해석, 양자역학, 파동 |
| 행렬 지수 | $$e^A = \sum_{n=0}^{\infty} \frac{A^n}{n!}$$ | $$A \in \mathbb{R}^{n \times n}$$ | $$\mathbb{R}^{n \times n}$$ | 행렬에 대한 지수함수 (테일러 급수) | 선형 시스템, 미분방정식 |
| 시간 종속 행렬 지수 | $$e^{M(x)}$$ | $$x \in \mathbb{R},\ M(x) \in \mathbb{R}^{n \times n}$$ | $$\mathbb{R}^{n \times n}$$ | 입력값에 따라 달라지는 행렬의 지수 | 제어이론, 동적 시스템 |