표본평균, 표본비율, 표본분산의 순입니다.
표준오차(Standard Error, SE)는 통계에서 표본평균, 표본분산, 표본비율 등의 표본 통계량이 반복적인 표본추출에서 모평균, 모분산, 모비율가 얼마나 차이가 나는 지를 나타냅니다. 즉, 표본 통계량의 모수에 대한 변동성을 나타내는 척도입니다.
표준오차는 표본추출 과정에서 발생하는 변동성으로 설명됩니다. 표본추출이 무작위적이므로, 각 표본에서 계산된 통계량이 다를 수밖에 없으며, 이 변동성을 표준오차로 표현합니다.
1. 표본크기 (Sample Size, n)
표본 크기가 클수록 표준오차는 작아집니다. 표준오차는 표본크기($n$)의 제곱근이나 자유도($n-1$)에 반비례하여 감소합니다.
표본평균의 표준오차
$$SE_{\bar{x}} = \dfrac{s}{\sqrt{n}}$$
표본비율의 표준오차
$$SE_{\hat{p}} = \sqrt{\frac{\hat{p}(1 – \hat{p})}{n}}$$
표본분산의 표준오차
$$SE_{s^2} = s^2 \times \sqrt{\dfrac{2}{n-1}}$$
2. 표본의 변동성 (Sample Variability, 표본표준편차 s)
표본 내의 데이터 변동성이 클수록 표준오차도 커집니다. 표본 내의 데이터가 서로 많이 차이가 날수록 해당 표본에서 계산된 통계량이 모집단의 실제 값으로부터 더 멀리 떨어질 가능성이 큽니다. 예를 들어, 표본의 표준편차가 클수록 표본평균의 표준오차도 커집니다. 표본 내 데이터가 더 분산되어 있으면, 평균을 추정하는데 있어서 더 많은 불확실성이 존재하게 됩니다. 표본 내 데이터의 분산은 모집단의 변동성과 직접적인 관계가 있습니다.
3. 모집단의 변동성 (Population Variability, 모표준편차 $\sigma$)
모집단 자체의 변동성이 클수록 표본통계량의 변동성도 커질 수 있습니다. 모집단에서 데이터가 많이 퍼져 있으면, 추출된 표본이 더 다양한 값을 가질 수 있으며, 이로 인해 표본통계량이 크게 변동할 가능성이 있습니다. 모집단의 변동성이 작으면, 표본통계량이 안정적이어서 표준오차가 작아집니다.
4. 표본 추출 방법
표본이 무작위로 추출되었는지, 또는 계통적 추출이나 층화 추출 등 다른 방식으로 추출되었는지에 따라서도 표준오차가 영향을 받을 수 있습니다. 무작위 표본 추출은 보통 표본 통계량의 편향을 최소화하고, 표준오차를 더 정확하게 계산할 수 있도록 돕습니다. 반면, 표본 추출 방법이 체계적이지 않거나 편향된 방식일 경우 표본 오차가 증가할 수 있습니다.
많은 연구에서 연구자는 모집단의 평균이나 비율을 추론하는 데 더 관심을 가지기 때문에 표본평균과 표본비율의 표준오차가 많이 사용됩니다.
반면, 분산은 평균이나 비율의 변동성을 이해하는 데 유용한 값이지만 분산 자체의 변동성에는 관심이 덜 합니다. 따라 분산의 표준오차 연구의 주요 목표가 되는 경우는 상대적으로 적습니다. 예를 들어, 대부분의 연구에서 평균을 통해 모집단의 일반적인 성향을 파악하려고 하며, 분산 자체를 평가하는 경우는 품질 관리나 공정 분석 등 특수한 경우에 국한됩니다. 인공지능 분야에서도 표본분산의 표준오차는 다른 통계량의 표준오차에 비해 덜 자주 사용되는 경향이 있습니다.
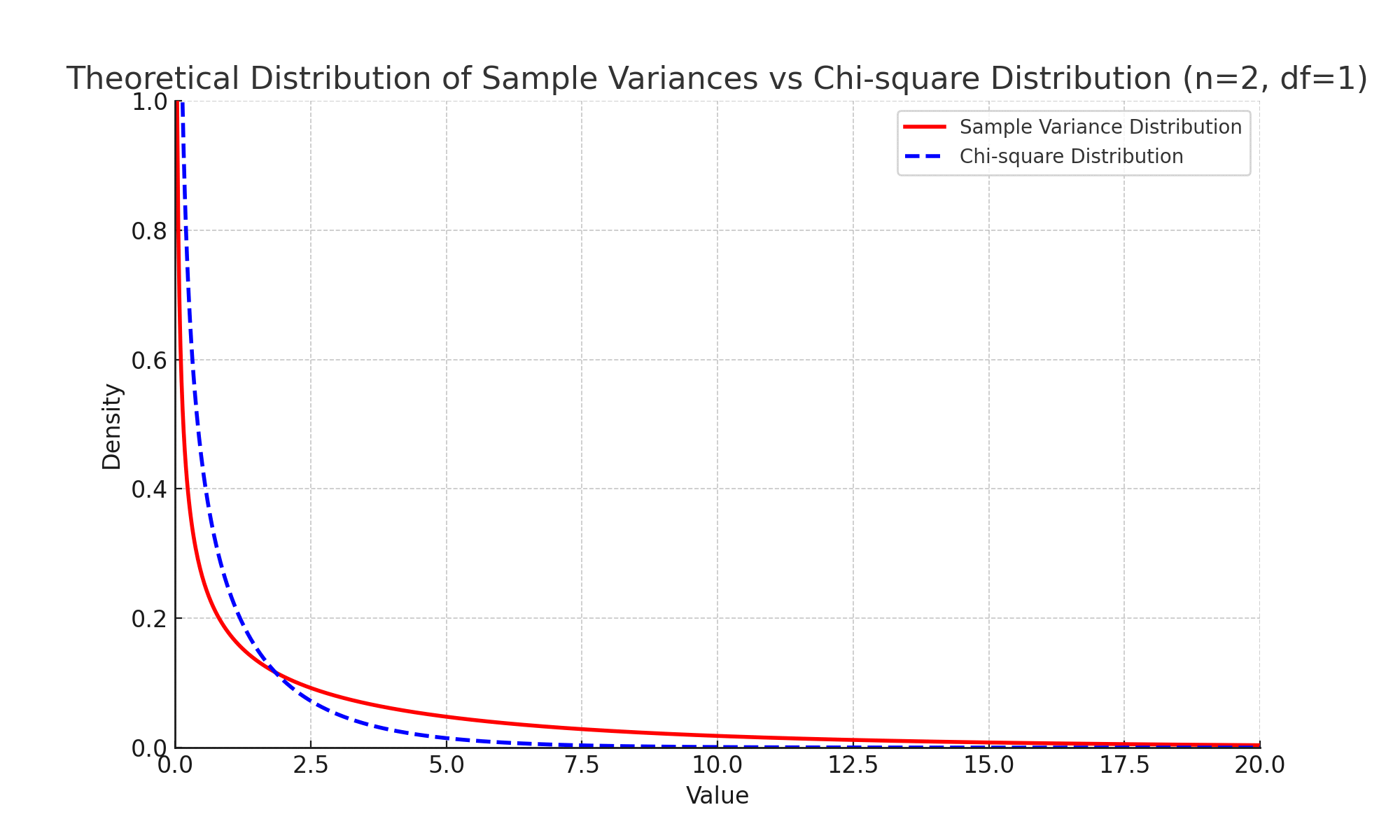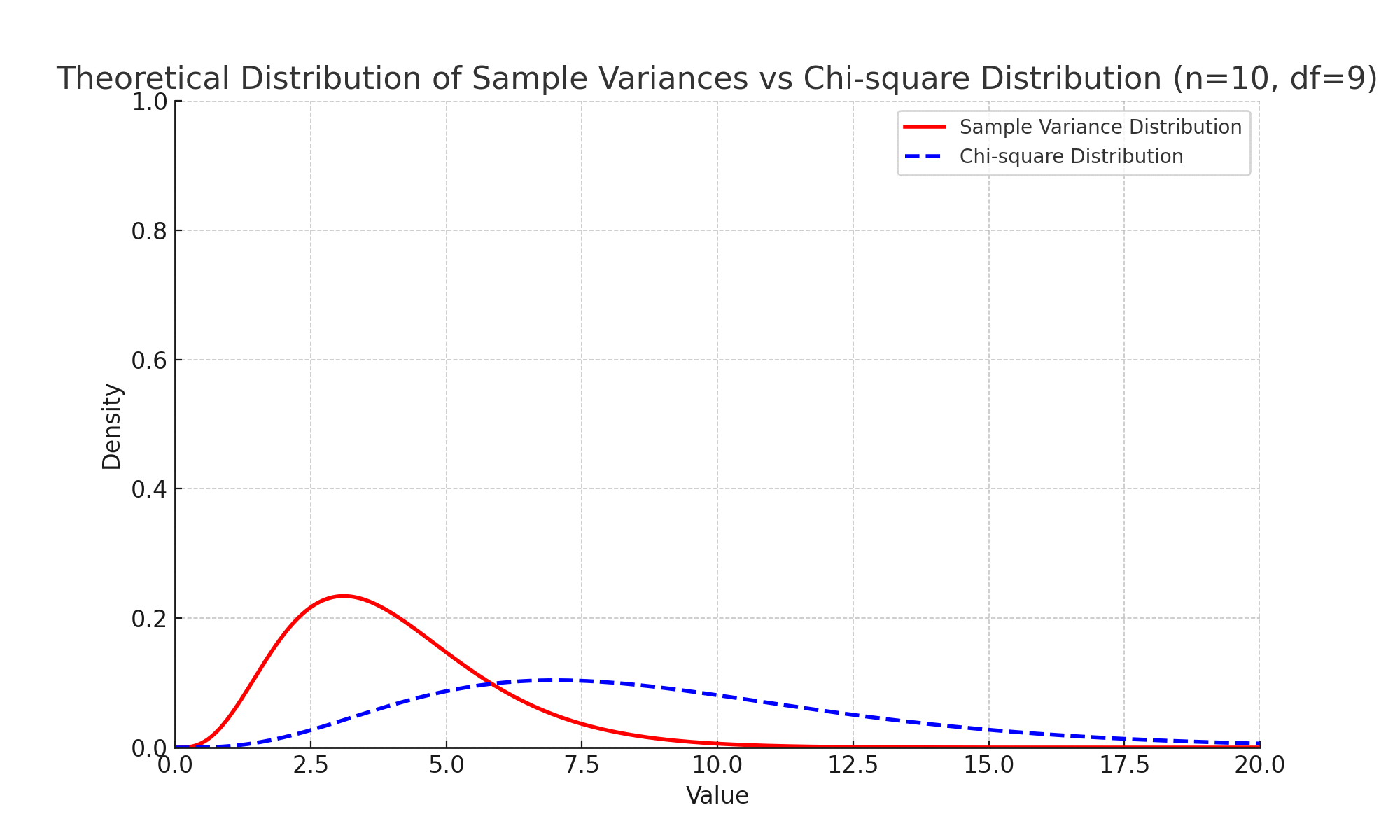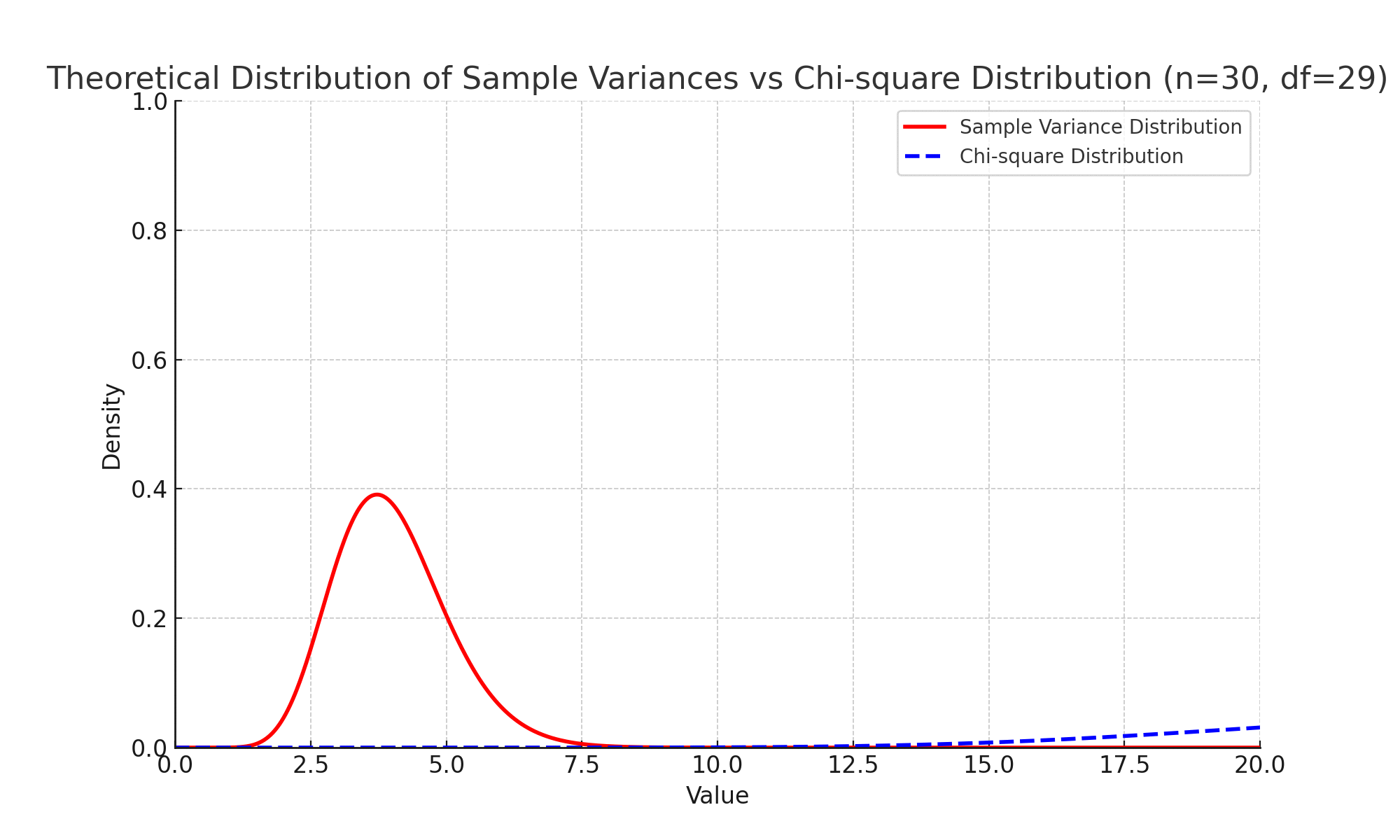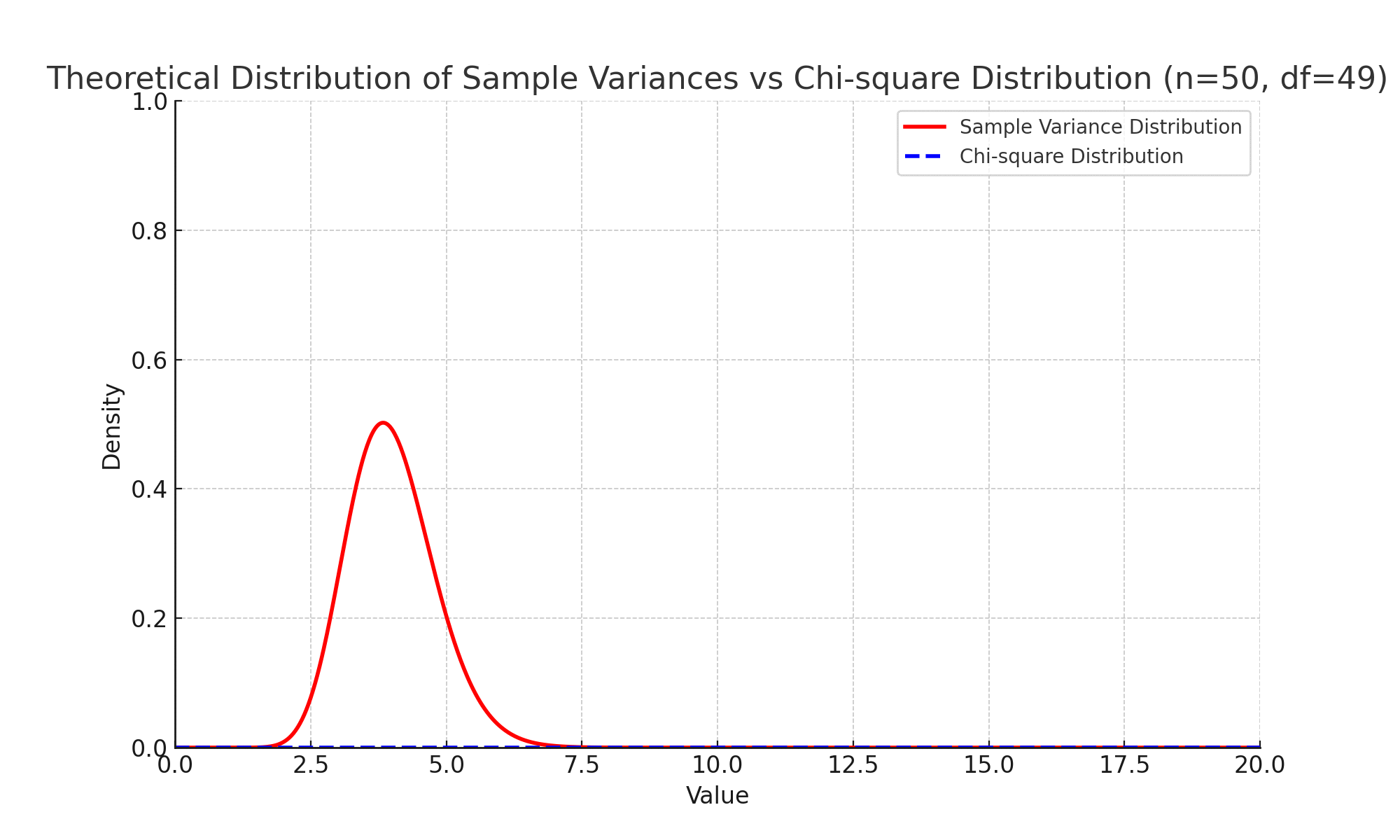
모집단이 정규분포를 따를 때 표본분산의 확률분포는 특정 형태를 가지며, 그 분포는 복잡한 함수로 기술됩니다. 이 함수는 일반적인 이름이 붙여진 표준분포(예: 정규분포, 카이제곱 분포 등)와 다릅니다.
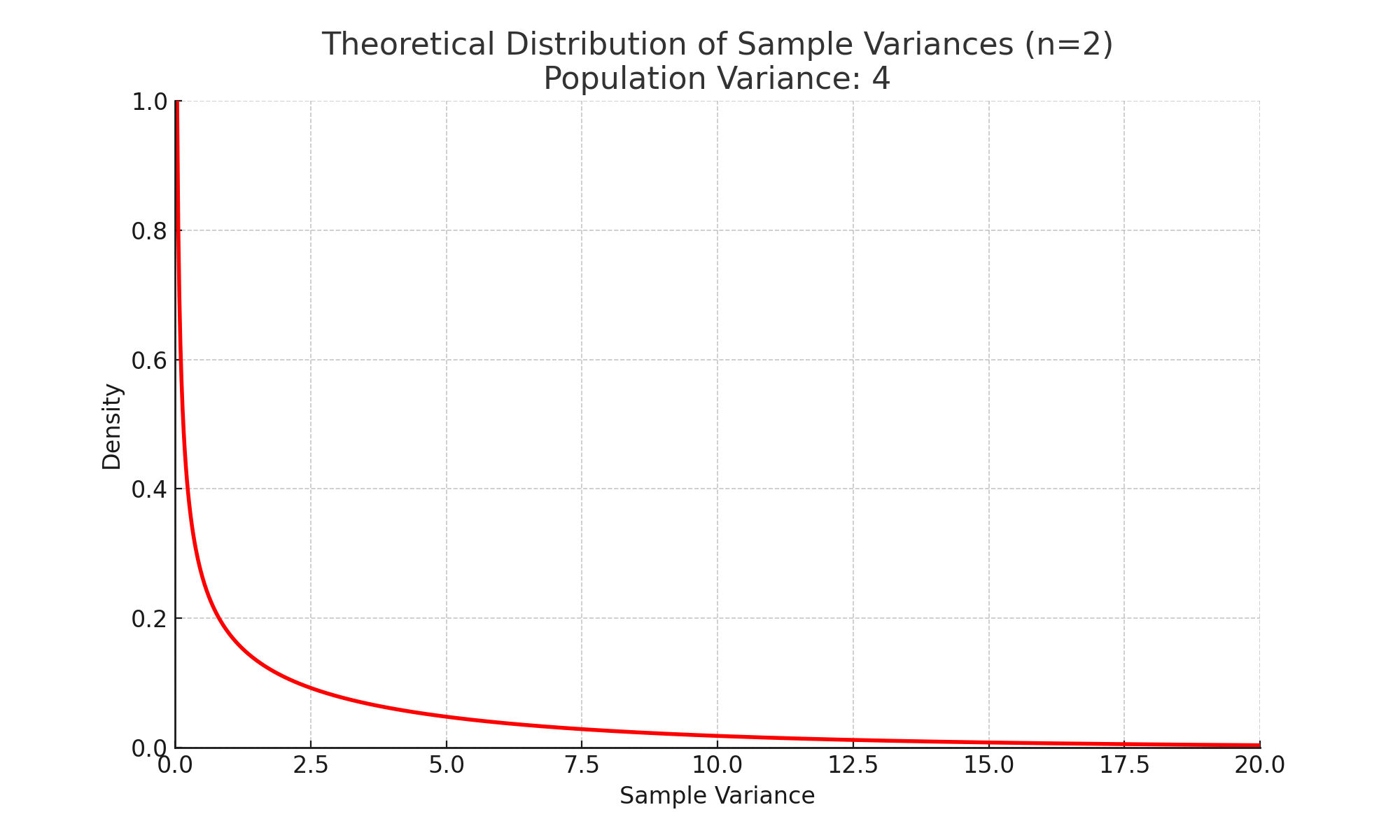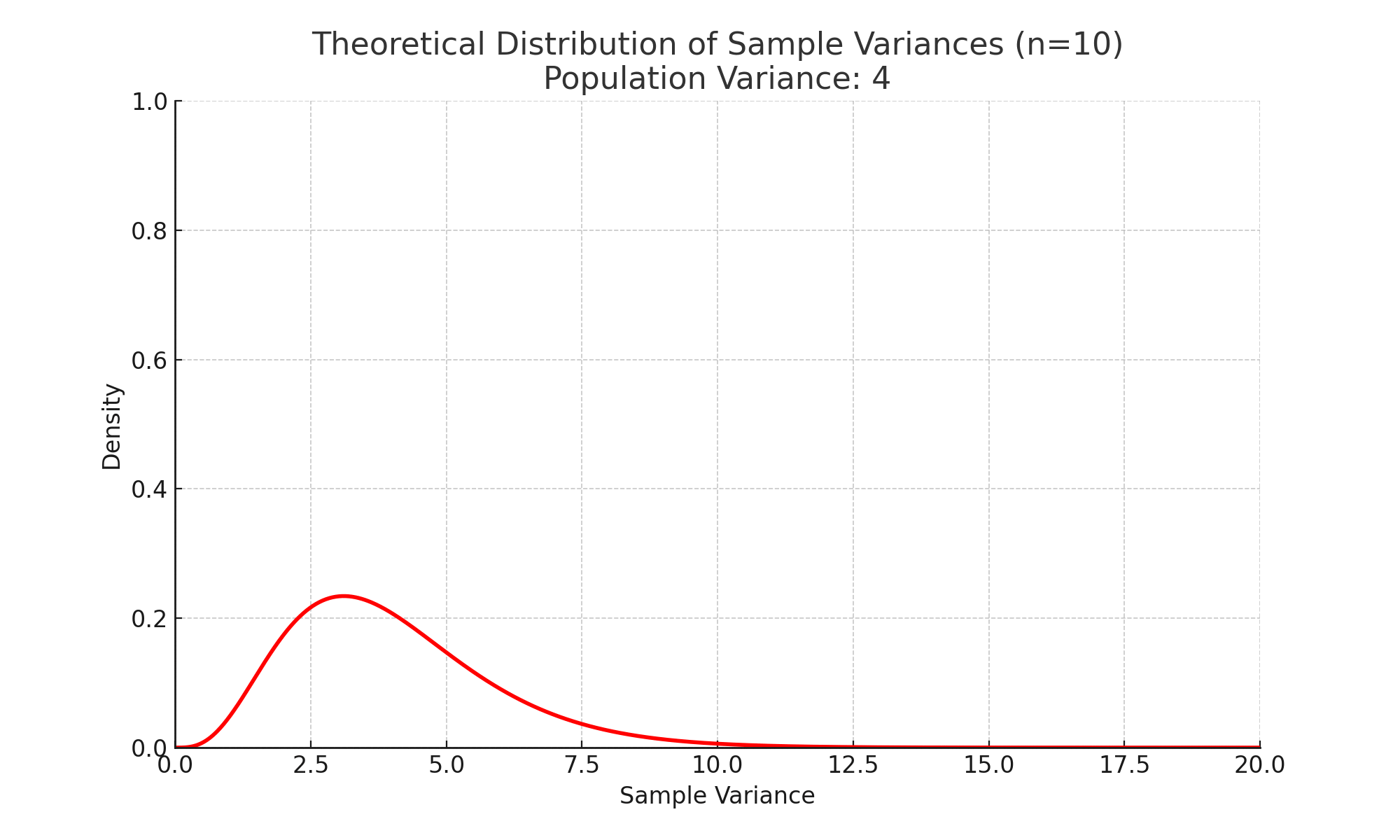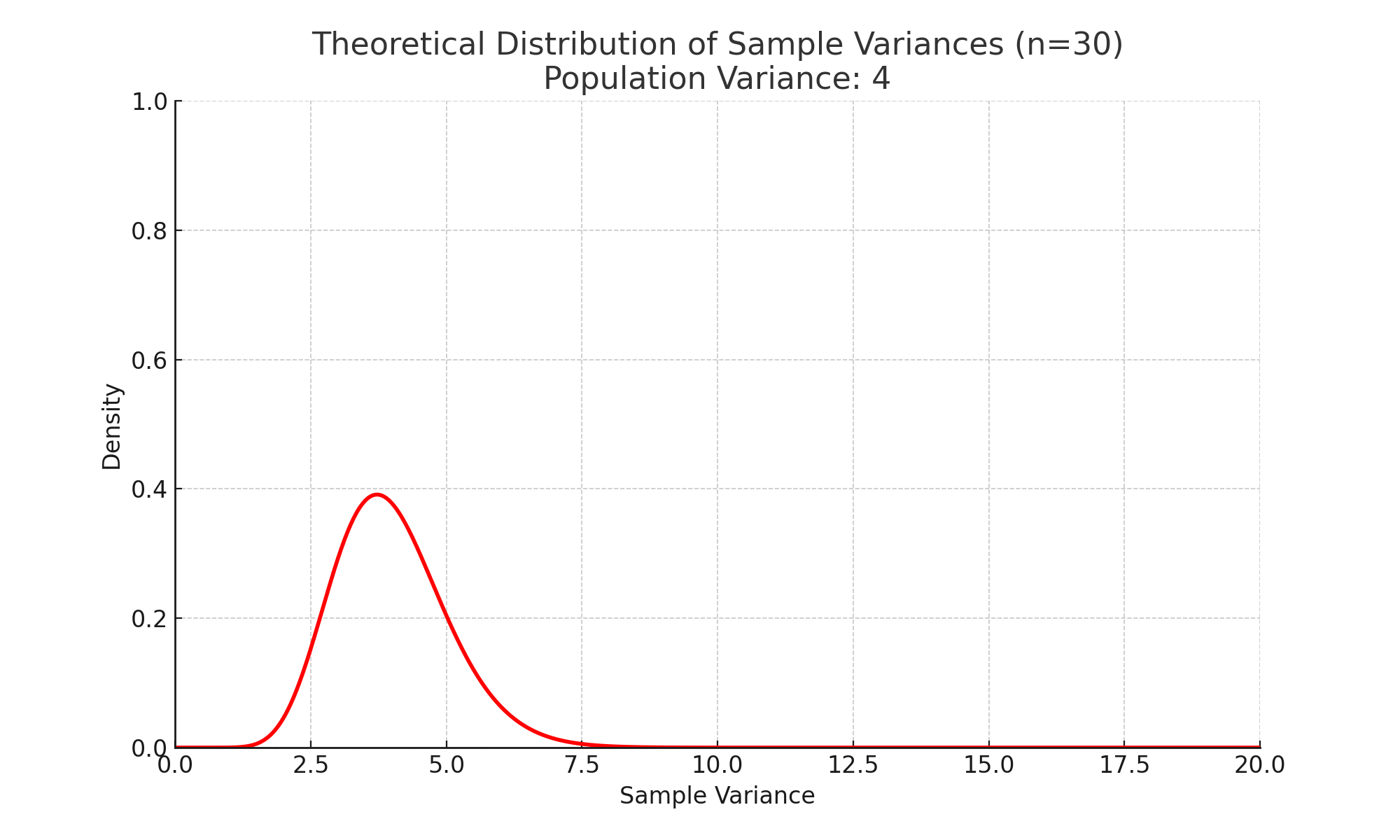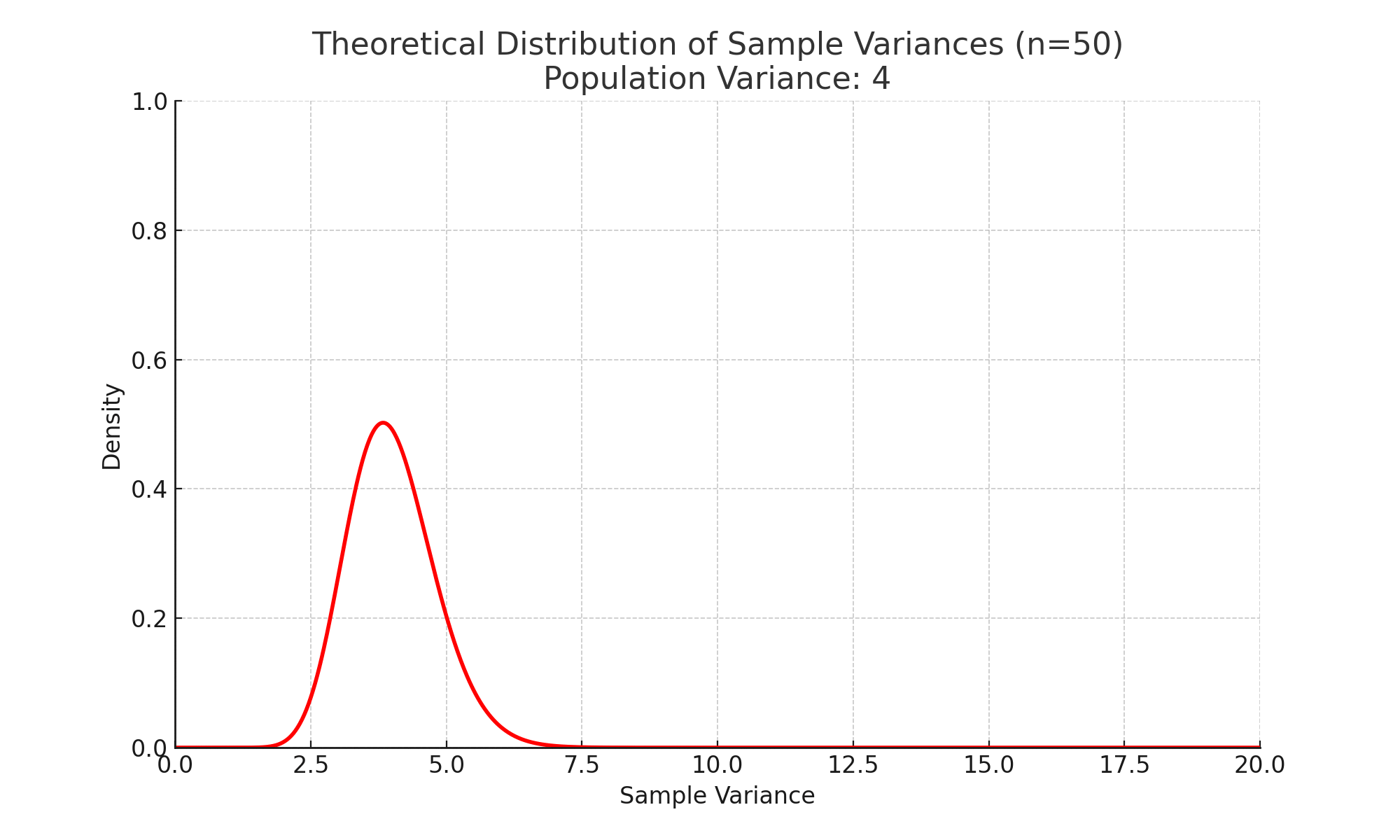
정규분포를 따르는 모집단에서, 표본분산을 통해 정의된 특정 통계량(예: $\dfrac{(n-1) \cdot S^2}{\sigma^2}$)은 카이제곱 분포를 따릅니다.