p값(p-value)은 연속적인 집합의 확률입니다.
p값은 관측된 데이터로 부터 구한 0에서 1사이의 실수입니다. 0에서 1사이의 실수는 주어진 누적분포함수(CDF)로 부터 구한 연속적인 집합의 확률입니다.
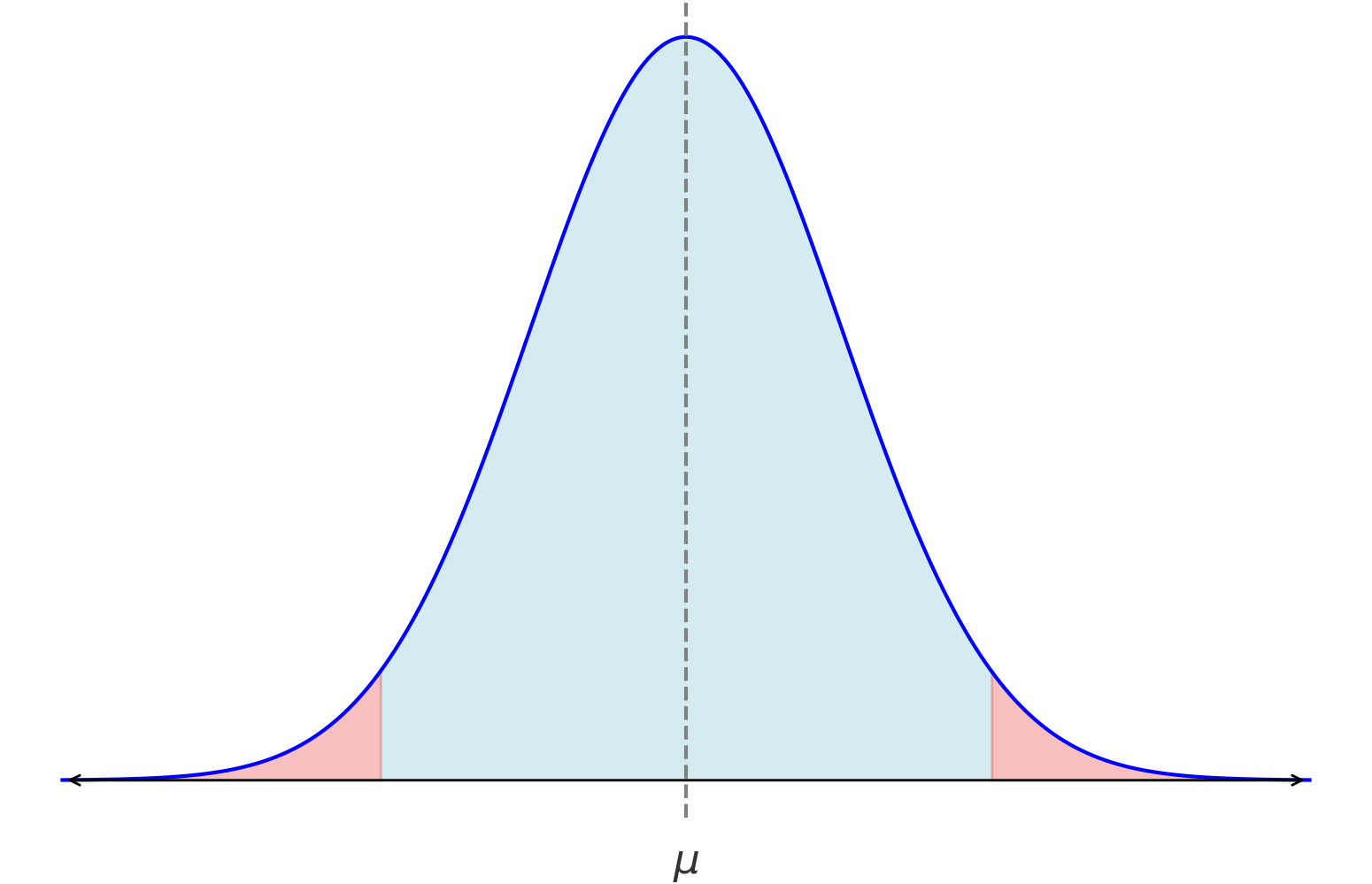
p값은 관측된 데이터가 특정 통계 분포(예: 정규분포)에서 얼마나 극단적인지를 나타내는 값입니다.
귀무가설이 참이라는 가정 하에, p값은 “관측된 데이터보다 더 극단적인 통계량에 해당하는 확률공간의 원소들의 비율”을 나타냅니다. 이때 p값은 연속적인 확률공간 내에서 귀무가설을 기각할지 말지를 결정하는 “경계점” 역할을 합니다.
유의수준(α)과 p값을 비교함으로써, 우리는 귀무가설을 기각할지를 결정하는데, 이 과정에서 p값은 연속적인 확률공간에서 경계 역할을 하게 됩니다.
이항 집합은 두 개의 상호 배타적인 결과(예: 성공/실패, 참/거짓)로 이루어진 집합을 의미합니다. 이 경우 확률은 두 가지 결과 중 하나가 발생할 가능성을 의미합니다.
p값은 이항적인 사건(두 가지 결과 중 하나)에 대한 확률이 아니라, 연속적인 확률공간(집합)에서 “관측된 통계량보다 더 극단적인 통계량을 얻을 확률”을 나타냅니다.
유의수준(α)은 이항집합의 확률이라고 볼 수 있습니다. 이항집합이란 두 개의 상호 배타적인 결과(예: 성공/실패, 참/거짓)를 나타내는 집합을 의미하는데, 유의수준은 그 중 하나의 경우, 즉 귀무가설을 **잘못 기각하는 경우(제1종 오류, Type I error)**가 발생할 확률을 나타냅니다.
집합은 원소들의 모임입니다. 공간은 집합에 추가적인 구조를 부여한 것입니다. 예를 들어 확률공간은 집합에 확률측도가 부여된 경우, 즉 확률적으로 해석할 수 있는 구조가 추가된 집합입니다. 벡터공간은 원소들이 벡터이고 이들 사이에 덧셈과 스칼라곱셈이 정의된 집합입니다. 위상공간은 집합에 특정한 열린 집합들의 체계(위상)이 정의된 경우입니다.
확률공간(Probability Space)의 세가지 요소