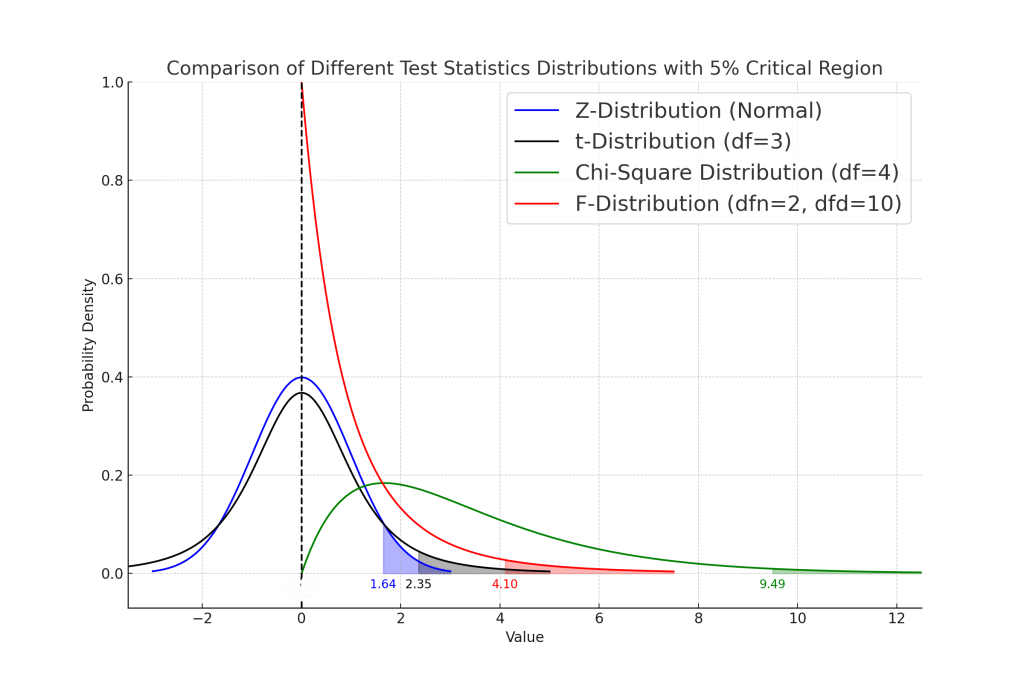
네, 검정통계량은 확률분포를 가지는 확률변수입니다. 무작위 표본으로부터 계산되는 통계량이기 때문입니다.
검정통계량은 주어진 표본 데이터에서 계산되는 통계량 중 하나입니다. 이 통계량은 모집단의 모수를 추정하거나 가설을 검정하는 데 사용되어 검정통계량이라고 부릅니다. 검정통계량은 특정 확률변수를 검정의 종류에 따른 확률분포의 확률변수로 변환하는 식이며, 이는 표본의 구성이나 크기에 따라 달라집니다. 예를 들어, t검정에서 사용되는 t통계량은 표본의 표본평균 등, 표본의 통계량에서 계산되며 t분포를 따릅니다. 마찬가지로, 카이제곱검정에서는 카이제곱통계량이 카이제곱분포를 따릅니다.
Z통계량의 확률분포함수는 자유도라는 매개변수(parameter)가 없고 이외의 검정통계량의 확률분포함수는 매개변수로 자유도를 가집니다. “표본내 개체의 자유도”는 표본크기, “표본내 집단의 자유도”는 표본내 집단수로부터 구합니다. “표본내 개체의 자유도”는 “표본내 집단의 자유도”와 “집단내 개체의 자유도”의 합입니다.
$$(n-1)=(k-1)+(n-k)$$
여기서, $n$은 표본크기
$(n-1)$은 “표본내 개체의 자유도” 또는 “표본의 자유도”
$k$는 표본내 집단수: t통계량에서 $k=2$
$(k-1)$은 “표본내 집단의 자유도”
$(n-k)$는 “집단내 개체의 자유도”
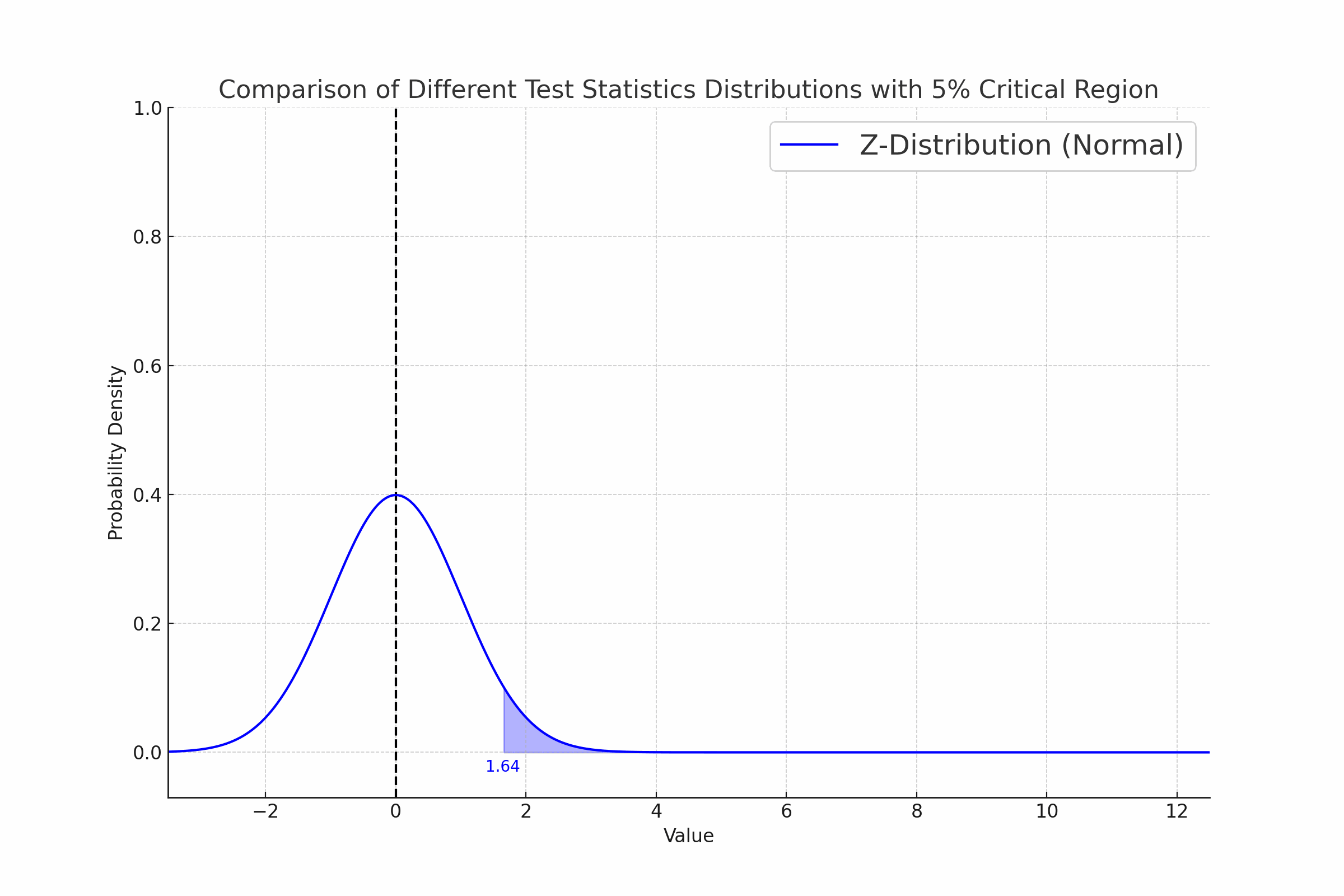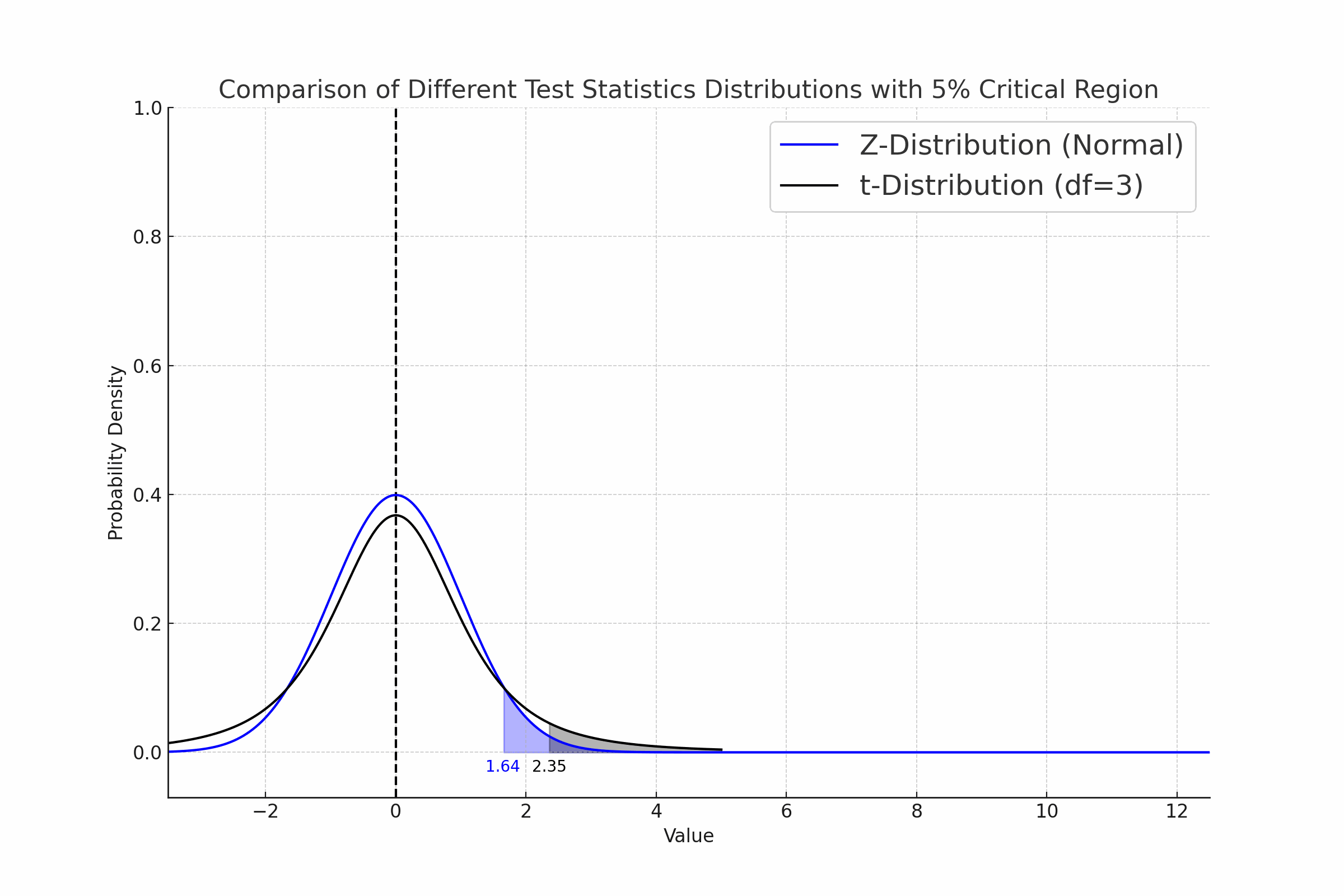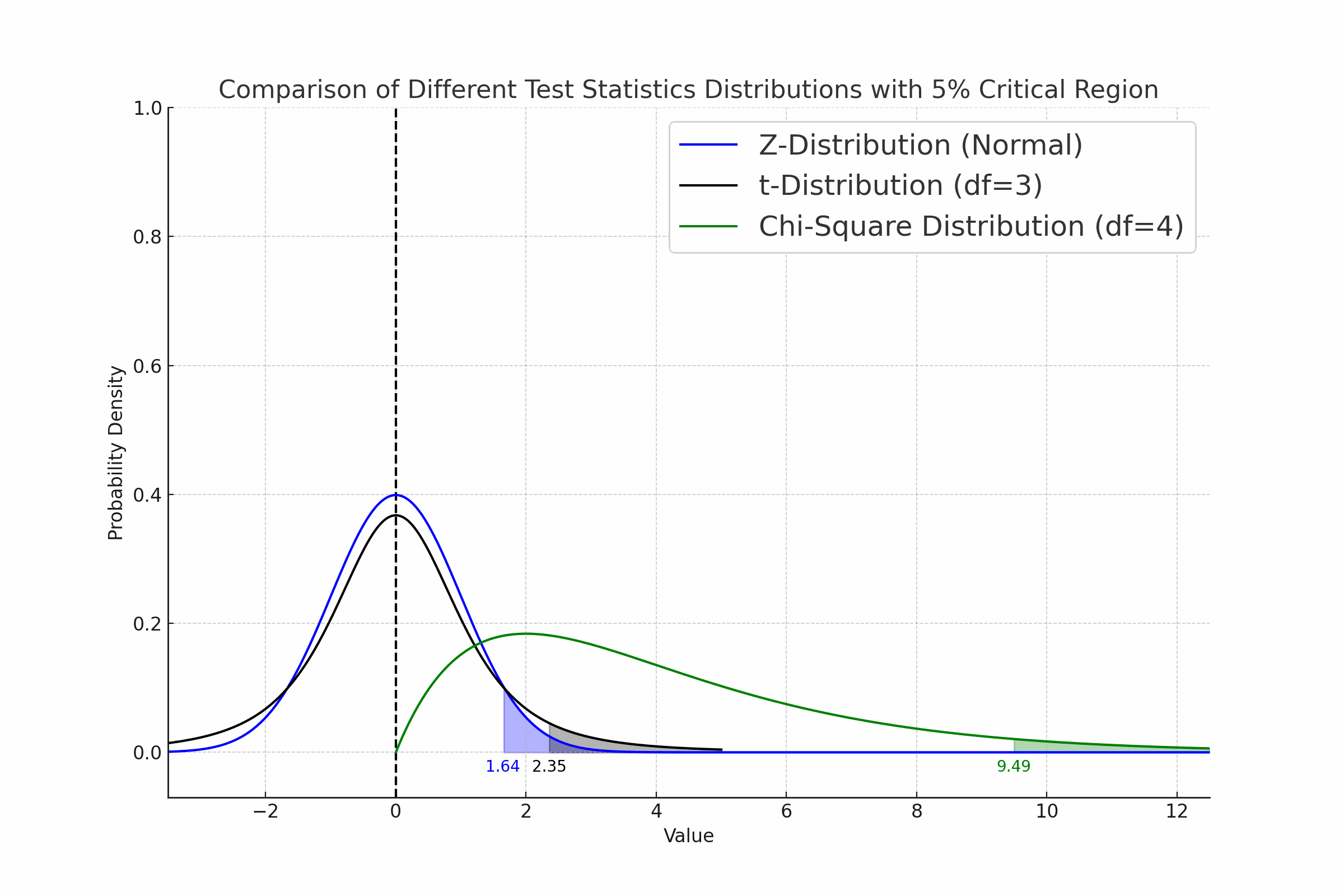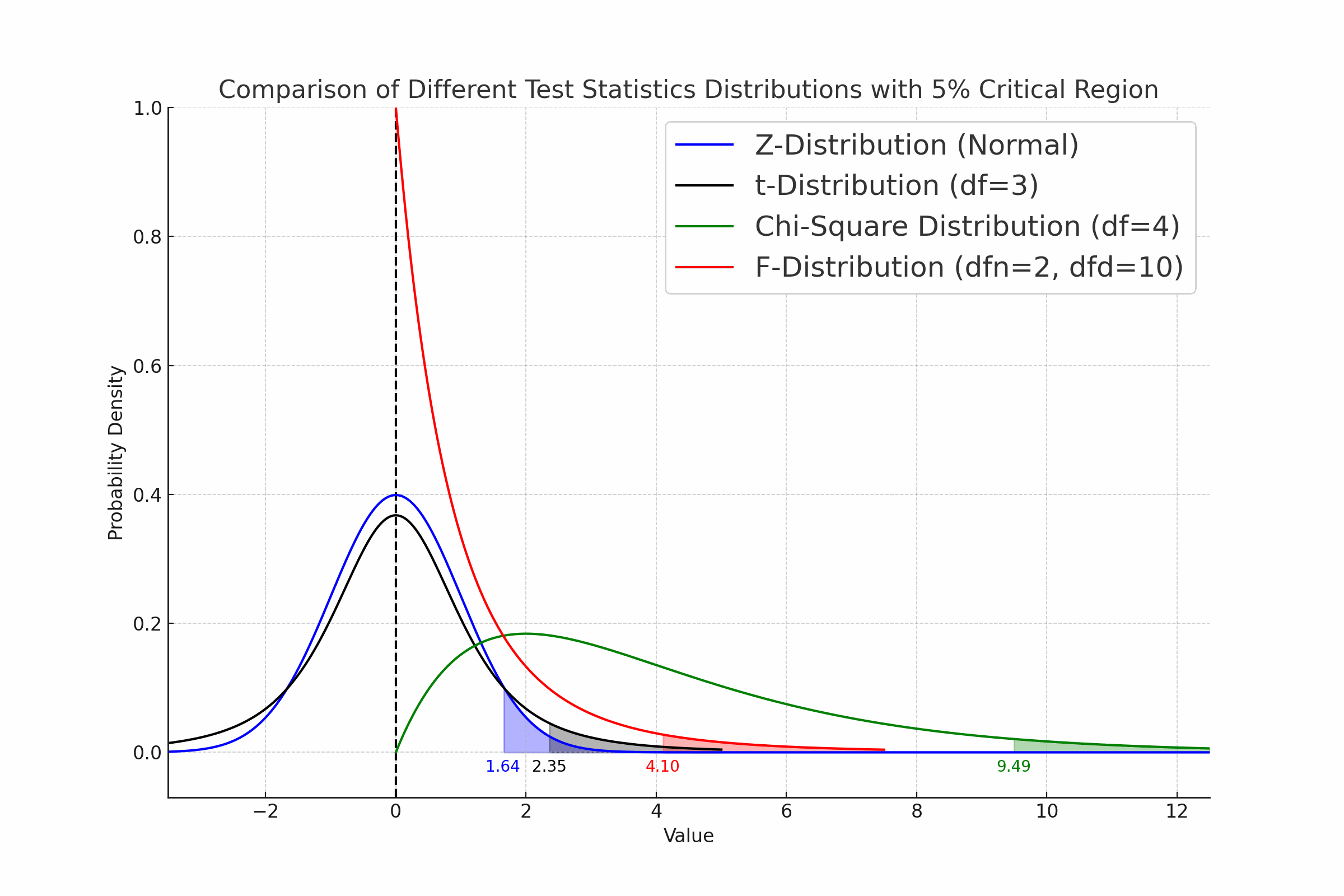
주요 검정통계량으로는 Z통계량, t통계량, 카이제곱통계량, F통계량 등 4종류의 통계량이 있습니다. Z통계량, t통계량, 카이제곱통계량, F통계량, 모두 데이터포인트(Data Point)가 정규분포를 나타낼 때 유도된 통계량입니다. 개체(데이터포인트)의 정규성 가정이 충족될 때, 각 통계량이 따르는 분포인 Z분포, t분포, 카이제곱분포, F분포를 사용할 수 있습니다.
표본크기가 충분히 크면 중심극한정리(Central Limit Theorem, CLT)에 의해 표본평균과 표본분산의 분포가 정규분포에 근사하게 됩니다. 이 때문에 원래 확률변수인 데이터포인트(Data Point)가 정규분포를 따르지 않더라도 표본의 크기가 충분히 크다면, 정규성 가정이 충족될 수 있습니다.
Z통계량(Z-Statistic)은 확률변수입니다. Z통계량의 확률분포는 표준정규분포(Standard Normal Distribution)를 따릅니다. Z통계량은 Z검정(Z-test)에서 사용됩니다. Z검정은 모집단의 표준편차가 알려져 있거나 표본의 크기가 충분히 클 때 모표준편차 대신에 표본표준편차를 사용하여 수행할 수도 있습니다.
$$Z = \dfrac{X – \mu}{\sigma}$$
여기서, $Z$는 표준정규분포를 나타내는 확률변수
$X$는 정규분포를 나타내는 확률변수: $X \sim N(\mu, \sigma^2)$
$\mu$는 모평균
$\sigma$는 모표준편차
$$Z = \dfrac{\bar{X} – \mu}{\dfrac{\sigma}{\sqrt{n}}}= \dfrac{\sqrt{n}(\bar{X} – \mu)}{\sigma}$$
여기서, $Z$는 Z통계량
$X$는 정규분포를 나타내는 확률변수: $X \sim N(\mu, \sigma^2)$
$\bar X$는 표본평균
$\mu$는 모평균
$\sigma$는 모표준편차
$n$은 표본크기
t통계량 (t-Statistic)은 확률변수입니다. t통계량의 확률분포는 t분포를 따릅니다. t통계량은 t검정(t-test)에서 사용됩니다. t검정은 모집단의 표준편차가 알려지지 않고 표본의 크기가 작은 경우에 수행합니다. t통계량으로 변환하는 식은 Z통계량을 변환하는 식에서 모표준편차를 표본표준편차로 대체한 것과 같습니다.
표본평균($\bar X$)을 t통계량으로 변환: 단일표본(1표본)
$$t = \dfrac{Z}{\sqrt{\dfrac{\chi^2}{n-1}}}=\dfrac{Z}{\sqrt{\dfrac{\dfrac{(n-1)s^2}{\sigma^2}}{n-1}}}=\dfrac{\dfrac{\bar X-\mu}{\dfrac{\sigma}{\sqrt{n}}}}{\dfrac{s}{\sigma}}=\dfrac{\bar{X} – \mu}{\dfrac{s}{ \sqrt{n}}}=\dfrac{\sqrt{n}(\bar{X} – \mu)}{s}$$
여기서, $t$는 t통계량
$Z$는 Z통계량: $Z=\dfrac{\bar X-\mu}{\dfrac{\sigma}{\sqrt{n}}}$
$\bar X$는 표본평균
$X$는 정규분포를 나타내는 확률변수: $X \sim N(\mu, \sigma^2)$
$\mu$는 모평균
$n$은 표본크기
$\sigma^2$는 모분산
$\sigma$는 모표준편차: $\sigma=\sqrt{\sigma^2}$
$n$은 표본크기
$\chi^2$은 카이제곱통계량: $\chi^2=\dfrac{(n-1)s^2}{\sigma^2}$
$(n-1)$은 표본의 자유도
$s^2$은 표본분산
$s$는 표본표준편차: $s=\sqrt{s^2}$
대응된 두 집단의 확률변수 차이평균($\bar D$)을 t통계량으로 변환: 대응표본
$$t = \dfrac{\bar D-(\mu_2-\mu_1)}{\dfrac{s_D} {\sqrt{n}}}=\dfrac{\bar X_2 -\bar X_1-(\mu_2-\mu_1)}{\dfrac{s_D} {\sqrt{n}}}=\dfrac{(\bar X_2 -\bar X_1)-\mu_0}{\dfrac{s_D} {\sqrt{n}}}$$
여기서, $t$는 t통계량
$\bar D$는 모든 대응된 쌍에 대해 계산된 차이 $d_i$의 평균: $\bar D=\dfrac{\sum\limits_{i=1}^{n}d_i}{n}$
$D$는 차이값($d_i$)들을 나타내는 확률변수: $D=X_2-X_1$ 또는 $d_i=x_{2i}-x_{1i}$
$x_{1i}$, $x_{2i}$는 각각 두 집단의 대응된 $i$번째 값
$d_i$는 두 집단에서 $i$번째 대응된 두 값의 차이
$\mu_1$과 $\mu_2$는 두 집단의 각각의 모평균: 귀무가설에서 $(\mu_2-\mu_1)=\mu_0=0$
$X_1$, $X_2$는 정규분포를 나타내는 대응된 확률변수
$x_{2i}$는 2번째 집단의 $i$번째 값
$x_{1i}$는 1번째 집단의 $i$번째 값
$s_D$는 차이값 $d_i$들의 표본표준편차값
$n$은 대응된 쌍의 수
자유도: $df=n-1$
$$t =\dfrac{\bar D-(\mu_2-\mu_1)}{\sqrt{\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}}}= \dfrac{\bar{X}_2 – \bar{X}_1-(\mu_2-\mu_1)}{\sqrt{\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}}}= \dfrac{(\bar{X}_2 – \bar{X}_1)-\mu_0}{\sqrt{\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}}}$$
여기서, $t$는 t통계량
$\bar D$는 독립된 두 확률변수 $X_1$과 $X_2$의 표본평균의 차이: $\bar D=\bar X_2-\bar X_1$
$\bar X_1$과 $\bar X_2$는 각각 첫 번째와 두 번째 표본의 평균: $\bar X_2-\bar X_1=\bar D$
$\mu_1$과 $\mu_2$는 독립된 두 집단의 모평균: 귀무가설에서 $(\mu_2-\mu_1)=\mu_0=0$
$s_1^2$과 $s_2^2$ 각각 첫 번째와 두 번째 표본의 분산
$n_1$과 $n_2$는 각각 첫 번째와 두 번째 표본의 크기
$$t = \dfrac{\bar{X}_2 – \bar{X}_1-\mu_0}{\sqrt{\dfrac{s_p^2}{n_1} + \dfrac{s_p^2}{n_2}}}$$
여기서, $t$는 t통계량
$\bar X_1$과 $\bar X_2$는 각각 첫 번째와 두 번째 표본의 평균
$\mu_0$는 두 집단의 모평균의 차이: 귀무가설에서 $\mu_0=\mu_2-\mu_1=0$
$s_p^2$은 통합분산(Pooled Variance): $s_p^2 = \dfrac{(n_1 – 1) \cdot s_1^2 + (n_2 – 1) \cdot s_2^2}{(n_1-1)+(n_2-1)}$
$s_1^2$과 $s_2^2$는 각각 첫 번째와 두 번째 표본의 분산
$n_1$과 $n_2$는 각각 첫 번째와 두 번째 표본의 크기
자유도: $df = (n_1-1)+(n_2-1)=n_1 + n_2 – 2$
$$t = \dfrac{\bar{X}_2 – \bar{X}_1-(\mu_2-\mu_1)}{\sqrt{\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}}}= \dfrac{(\bar{X}_2 – \bar{X}_1)-\mu_0}{\sqrt{\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}}}$$
여기서, $t$는 t통계량
$\bar X_1$과 $\bar X_2$는 각각 첫 번째와 두 번째 표본의 평균
$\mu_0$는 두 집단의 모평균의 차이: 귀무가설에서 $\mu_0=\mu_2-\mu_1=0$
$s_1^2$과 $s_2^2$는 각각 첫 번째와 두 번째 표본의 분산값
$n_1$과 $n_2$는 각각 첫 번째와 두 번째 표본의 크기
자유도: $df = \dfrac{\left(\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2}\right)^2}{\dfrac{\left(\dfrac{s_1^2}{n_1}\right)^2}{n_1 – 1} + \dfrac{\left(\dfrac{s_2^2}{n_2}\right)^2}{n_2 – 1}}$
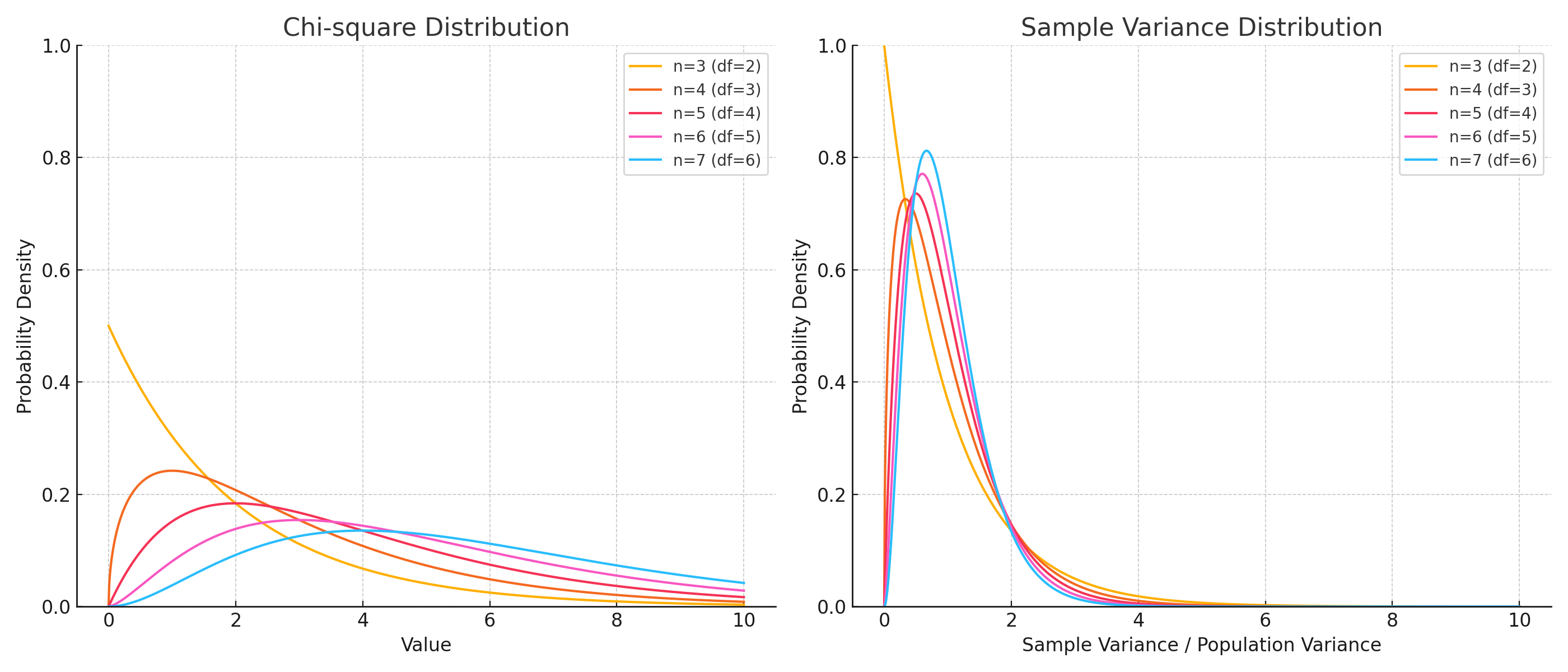
카이제곱통계량 ($\chi^2$-Statistic)은 확률변수입니다. 카이제곱통계량의 확률분포는 카이제곱분포를 따릅니다. 카이제곱통계량은 카이제곱검정($\chi^2$-test)에서 사용됩니다. 카이제곱분포의 형태는 자유도에 따라 결정됩니다.
$$\chi_m^2 = Z_1^2+Z_2^2+\cdots+Z_m^2=\sum\limits_{i=1}^{m} Z_i^2$$
여기서, $Z_i$는 평균이 0이고 분산이 1인 표준정규분포를 따르는 독립적인 확률변수: $Z_i \sim N(0,1)$
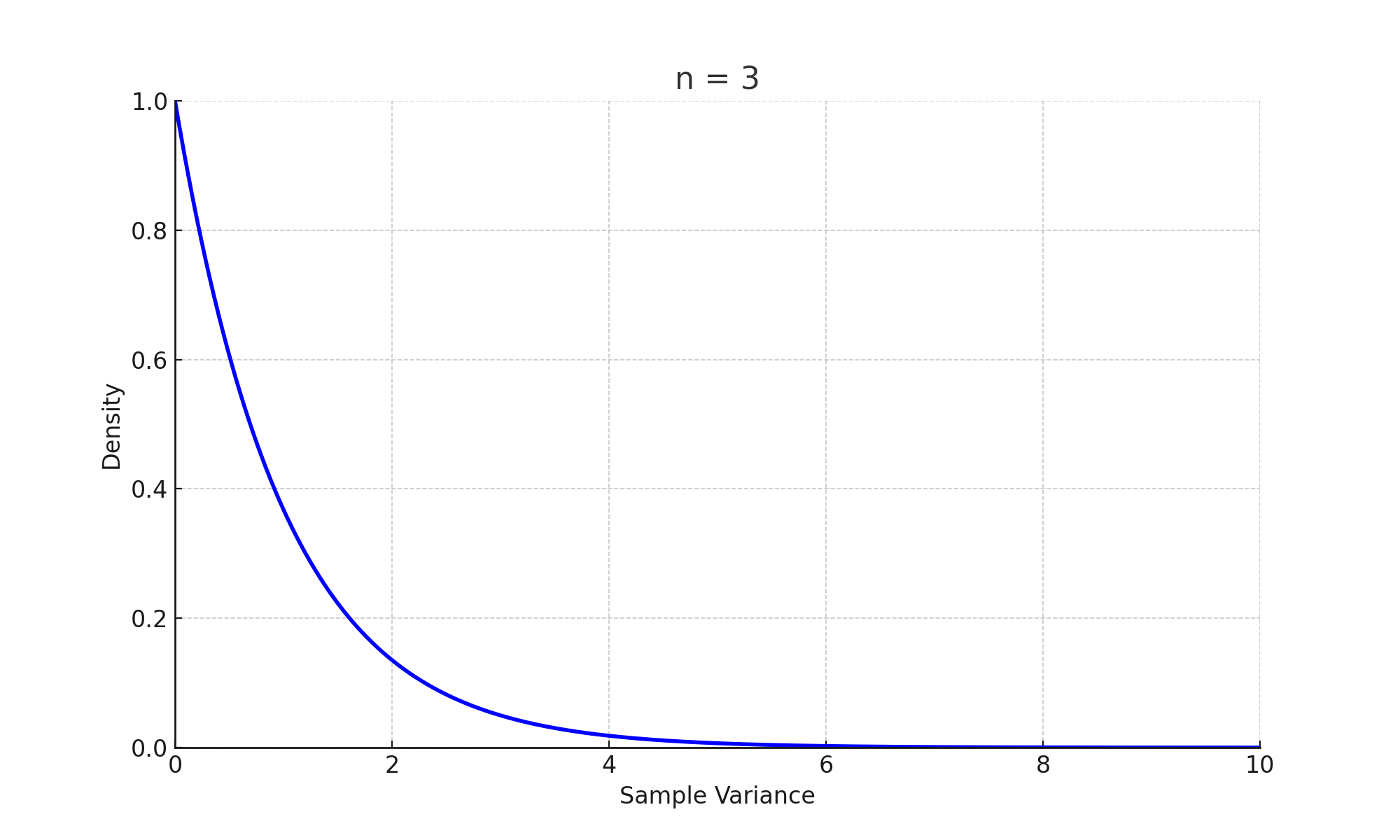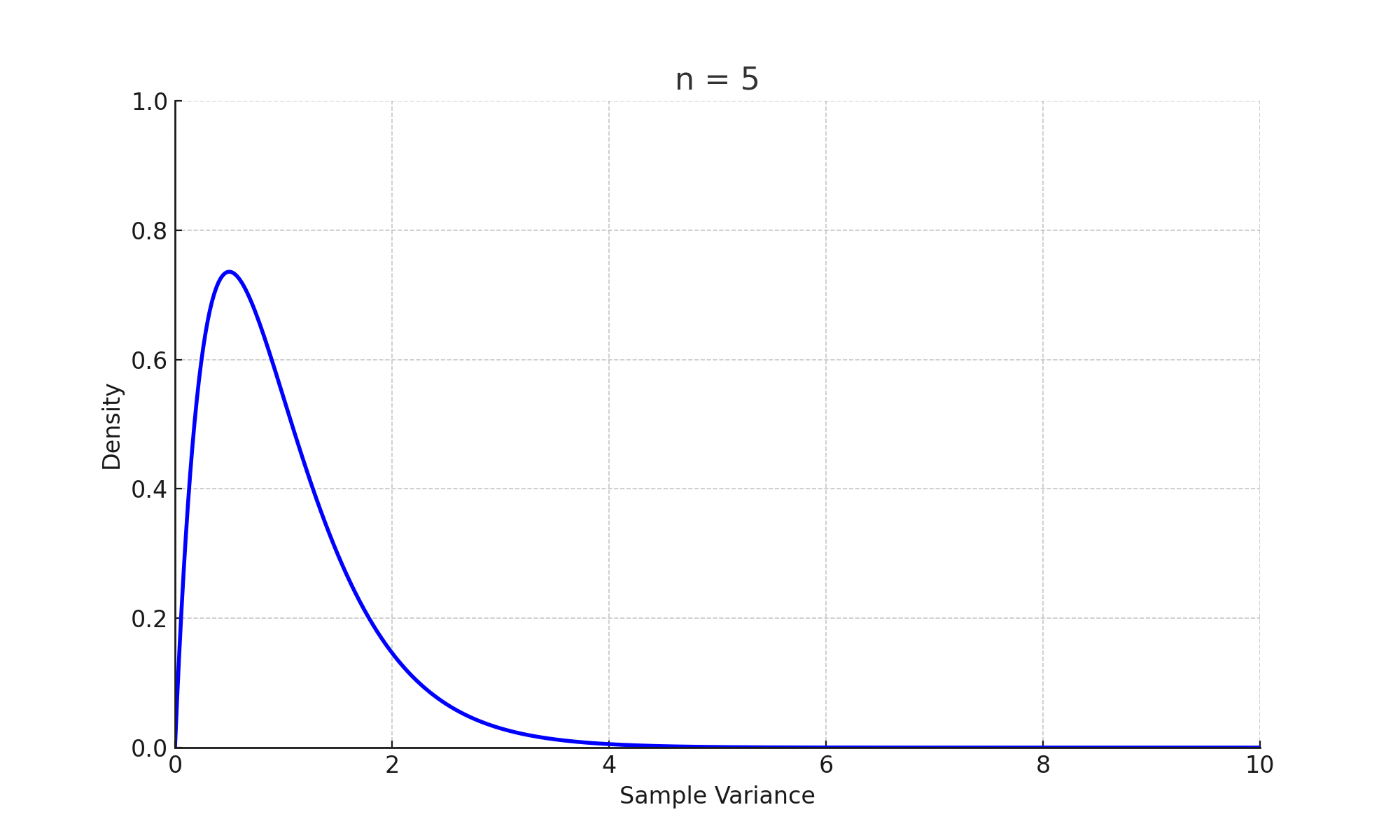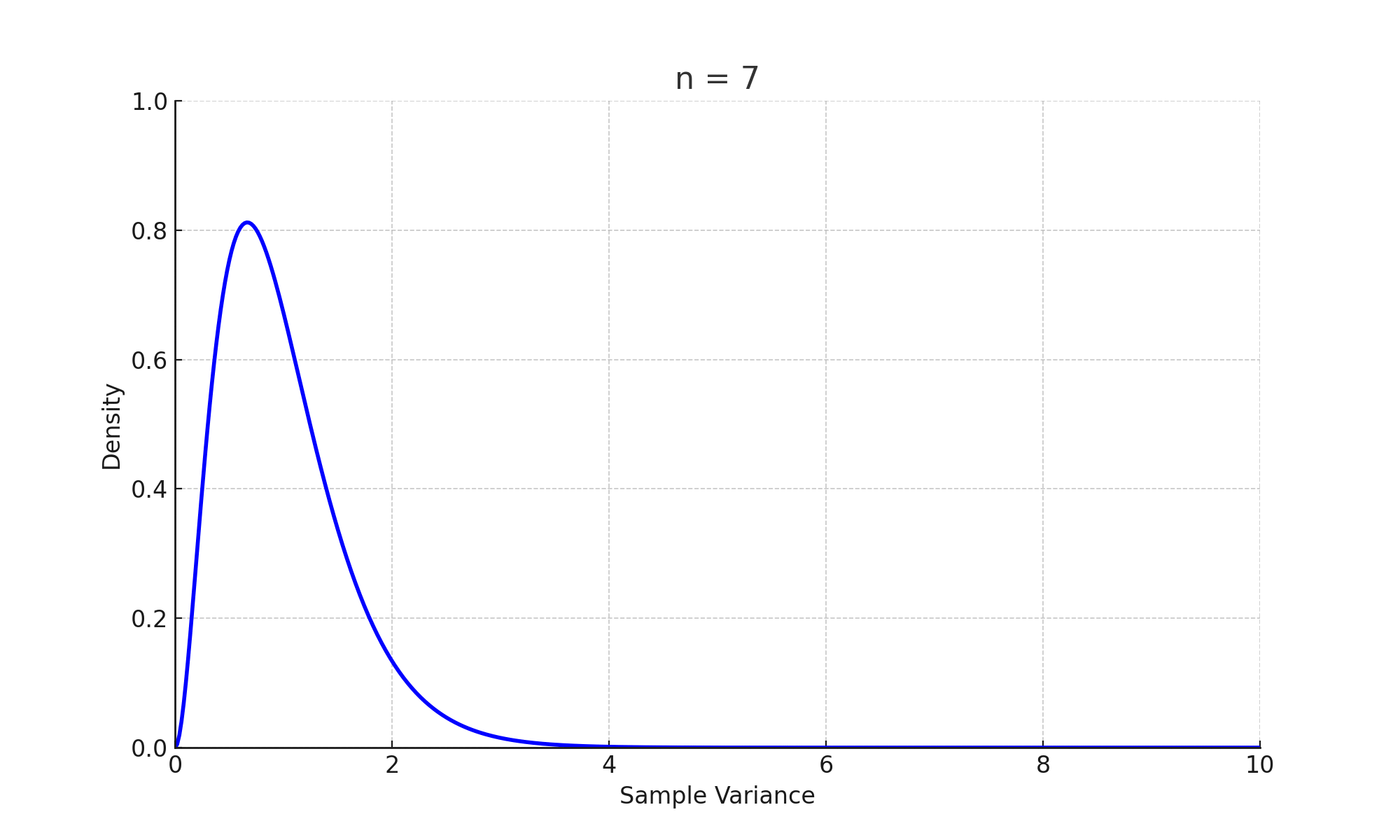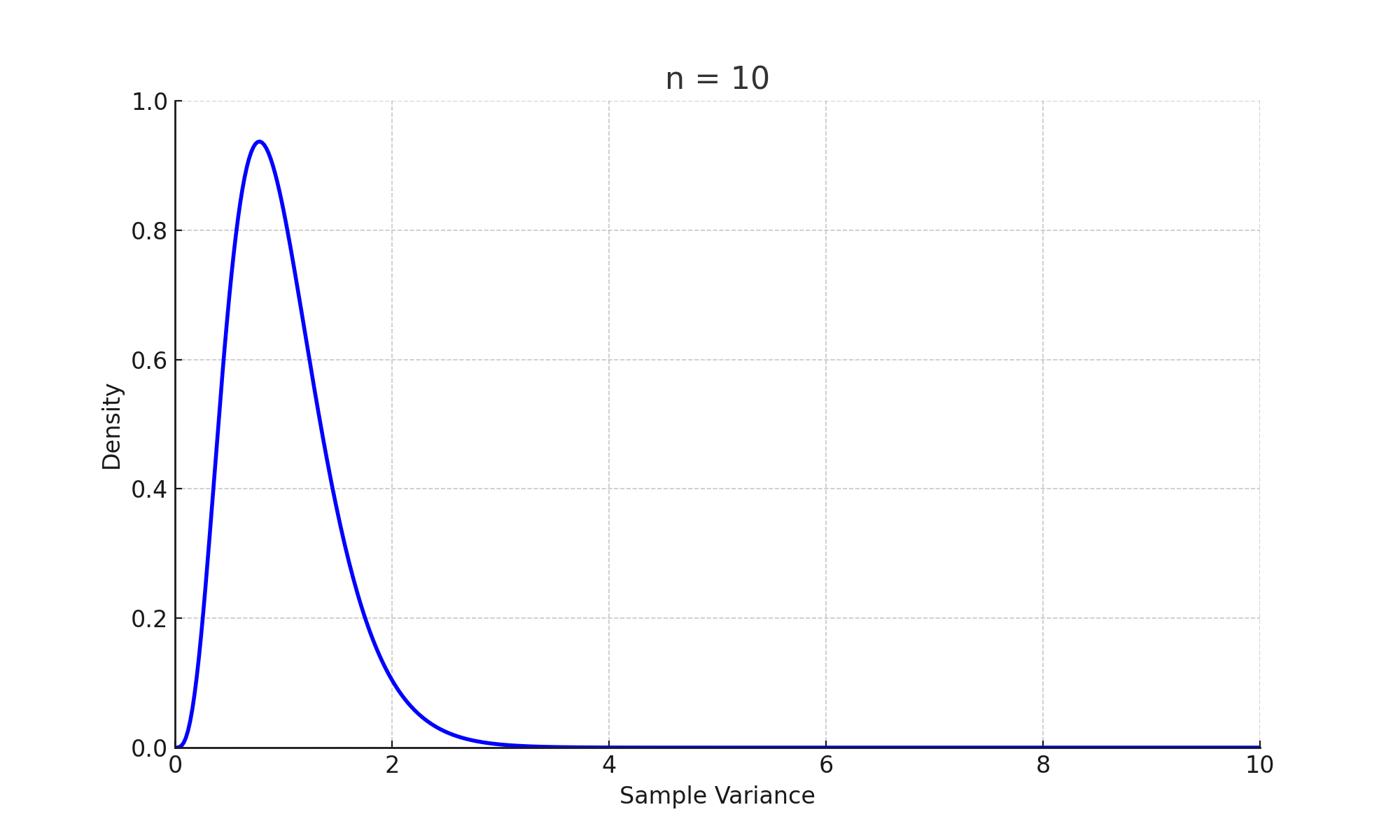
$$\chi^2_{n-1}=\dfrac{(n-1)s^2}{\sigma^2}$$
여기서, $\chi^2_{n-1}$은 자유도가 $(n-1)$인 카이제곱통계량
$n$은 표본크기
$s^2$은 표본분산
$\sigma^2$은 모분산
$$\chi^2_{k-1}=\dfrac{(k-1)s_B^2}{\sigma_B^2}=\dfrac{(k-1)MS_B}{\sigma_B^2}=\dfrac{SS_B}{\sigma_B^2}$$
여기서, $s_B^2$은 표본(Sample)내 각 집단의 분산: $s_B^2=MS_B$
$\sigma_B^2$은 집단(수준, 그룹, Group)의 모분산: 모집단(Population)내 각 집단의 분산
$k$는 표본내 집단수
$(k-1)$은 표본내 집단의 자유도: $df_B=k-1$
$SS_B$(Sum of Squares Between, 집단간변동)은 개체의 각 집단의 평균성분과 전체평균 간 차이의 제곱의 합: $SS_B = \sum\limits_{i=1}^{k} n_i (\bar{X}_i – \bar{X})^2$
$n_i$는 표본내 $i$번째 집단의 크기
$\bar X_i$는 $i$번째 집단의 평균
$\bar X$는 표본평균
$n$은 표본의 크기: $n=\sum\limits_{i=1}^{k}n_i$
$MS_B$(Mean Squares Between, 집단간분산)은 개체의 집단으로서의 변동: $MS_B=\dfrac{SS_B}{k-1}$
$$\chi^2_{n-k}=\dfrac{(n-k)s_W^2}{\sigma_W^2}=\dfrac{(n-k)MS_W}{\sigma_W^2}=\dfrac{SS_W}{\sigma_W^2}$$
여기서, $s_W^2$은 표본내 개체의 분산: $s_W^2=MS_W$
$\sigma_W^2$은 개체의 모분산: 모집단(Population)에서 개체의 분산
$SS_W$(Sum of Squares Within, 집단내변동)은 각 데이터포인트와 해당 집단평균 간 차이의 제곱의 합: $SS_W=\sum\limits_{i=1}^{k} \sum\limits_{j=1}^{n_i} (X_{ij} – \bar{X}_i)^2$
$k$는 표본내 집단수
$n$은 표본크기
$n_i$는 표본내 $i$번째 집단의 크기: $\sum\limits_{i=1}^k=n$
$X_{ij}$는 $i$번째 집단의 $j$번째 데이터값
${\bar X}_i$는 $i$번째 집단의 평균
$MS_W$(Mean Squares Wihti, 집단내분산)은 개체의 집단내에서의 변동: $MS_W=\dfrac{SS_W}{n-k}$
관측빈도수와 기대빈도수 차이의 카이제곱통계량으로 변환
$$\chi^2 = \sum \dfrac{(O_i – E_i)^2}{E_i}$$
여기서, $\chi^2$은 카이제곱통계량
$O_i$는 관측빈도(Observed Frequency)
$E_i$는 기대빈도(Expected Frequency)
$$df=k-1$$
여기서, k는 범주의 수 : 기대빈도 또는 관측빈도의 카테고리 수
$$df = (r – 1) \times (c – 1)$$
여기서, $r$는 행(row)의 수
$c$는 열(column)의 수
변동분해 공식
$$SS_T=SS_B+SS_W$$
여기서, $SS_T$(Total Sum of Squares)은 총변동
$SS_B$(Sum of Squares Between groups)은 집단간변동
$SS_W$(Sum of Squares Within groups)은 집단내변동
자유도 공식
$$n-1=(k-1)+(n-k)$$
여기서, $(n-k)$는 표본내 개체의 자유도: $df_B=n-k$
F통계량(F-Statistic)은 확률변수입니다. F통계량의 확률분포는 F분포를 따릅니다. F통계량은 F검정(F-test)에서 사용됩니다. F분포는 두 개의 자유도(분자와 분모의 자유도)에 따라 형태가 달라집니다.
F통계량은 두 개의 독립적인 카이제곱 분포를 따르는 변수의 비로 정의되며, 이는 등분산 가정이 충족될 때 F분포를 따르게 됩니다.
F검정은 두 개의 독립적인 표본분산을 비교하거나, 분산분석(ANOVA)에서 여러 집단 간의 차이를 분석할 때 사용됩니다. 이 과정에서 F통계량은 두 표본분산의 비로 계산되며, 이 비가 F분포를 따르게 됩니다.
$$F=\dfrac{\dfrac{\chi^2_{n_1-1}}{n_1-1}}{\dfrac{\chi^2_{n_2-1}}{n_2-1}}=\dfrac{\dfrac{s_1^2}{\sigma_1^2}}{\dfrac{s_2^2}{\sigma_2^2}}=\dfrac{s_1^2}{s_2^2}$$
$$F=\dfrac{\dfrac{\chi^2_{k-1}}{k-1}}{\dfrac{\chi^2_{n-k}}{n-k}}=\dfrac{\dfrac{s_B^2}{\sigma_B^2}}{\dfrac{s_W^2}{\sigma_W^2}}=\dfrac{\dfrac{MS_B}{\sigma_B^2}}{\dfrac{MS_W}{\sigma_W^2}}$$
여기서, $s_B^2$는 집단간분산: $s_B^2=MS_B$
$s_W^2$는 집단내분산: $s_W^2=MS_W$
$SS_B$(Sum of Squares Between)는 집단간변동의 관측값: $SS_B=\sum\limits_{i=1}^{k}n_i(\bar X_i-\mu)^2$
$SS_W$(Sum of Squares Within)는 집단내변동의 관측값: $SS_W=\sum\limits_{i=1}^{k}\sum\limits_{j=1}^{n_i}(X_{ij}-\bar X_i)^2$
$MS_B$(Mean Square Between)는 집단간분산(Between-group variance): $MS_B=\dfrac{SS_B}{k-1}$
$MS_W$((Mean Square Within))는 집단내분산(Within-group variance): $MS_W=\dfrac{SS_W}{n-k}$
$$ F = \dfrac{\sum\limits_{i=1}^{k} \dfrac{n_i (\bar{X}_i – \bar{X}_w)^2}{s_i^2}}{(k – 1)} \Bigg/ \dfrac{\sum\limits_{i=1}^{k} \dfrac{s_i^2}{n_i}}{df} $$
여기서, $\bar X_w$는 가중평균: $ \bar{X}_w = \dfrac{\sum\limits_{i=1}^{k} w_i \bar{X}_i}{\sum\limits_{i=1}^{k} w_i} $
$\omega_i$는 $i$번째 집단의 가중치: $ w_i = \dfrac{n_i}{s_i^2} $
$df$는 수정된 자유도: $ df = \dfrac{\left(\sum\limits_{i=1}^{k} \dfrac{w_i}{n_i}\right)^2}{\sum\limits_{i=1}^{k} \dfrac{w_i^2}{n_i^2 (n_i – 1)}} $
$$F_{1, n-1}=t^2_{n-1}$$
여기서, $n$은 대응된 쌍의 수
$$F_{1, n-2}=t^2_{n-2}$$
여기서, $n$은 표본크기: $n=n_1+n_2$
$$H_0: \sigma^2_1=\sigma^2_2$$
$$H_1: \sigma^2_1 \neq \sigma^2_2$$
$$\sigma^2_1=\sigma^2_2=\sigma^2$$
$$F_{test}=\dfrac{\dfrac{s^2_1}{\sigma^2_1}}{\dfrac{s^2_2}{\sigma^2_2}}=\dfrac{s^2_1}{s^2_2}$$
$$\mu_1=\mu_2= \cdots=\mu$$
$\mu_1\neq \mu_2$ or $\mu_2 \neq \mu_3$ or $\cdots$
$$\sigma^2_1=\sigma^2_2=\cdots=\sigma^2_B=\sigma^2$$
$$\sigma^2_W=\sigma^2$$
$$\therefore \sigma^2_B=\sigma^2_W=\sigma^2$$
여기서, $s_B^2$는 집단간분산(Between-group variance): $s_B^2=MS_B=\dfrac{SS_B}{k-1}$
$s_W^2$는 집단내분산(Within-group variance): $s_W^2=MS_W=\dfrac{SS_W}{n-k}$
$MS_B$(Mean Square Between)는 집단간분산의 관측값
$MS_W$((Mean Square Within))는 집단내분산의 관측값
$df_B$는 표본내 집단의 자유도: $df_B=k-1$
$df_W$는 표본내 개체의 자유도: $df_W=n-k$
$SS_B$(Sum of Squares Between)는 집단간변동의 관측값: $SS_B=\sum\limits_{i=1}^{k}n_i(\bar X_i-\mu)^2$
$SS_W$(Sum of Squares Within)는 집단내변동의 관측값: $SS_W=\sum\limits_{i=1}^{k}\sum\limits_{j=1}^{n_i}(X_{ij}-\bar X_i)^2$
| 분석 유형 | 모수검정 분산에 대한 정보로 평균, 분산 비교 | 비모수검정 분산에 대한 정보없이 분포 비교 |
|---|---|---|
| 대응된 두 집단의 차이평균 비교 | 대응표본 t검정 (Paired t-test) | 윌콕슨 부호순위검정 (Wilcoxon signed-rank test) |
| 대응된 두 집단의 중앙값 차이 비교 | – | 윌콕슨 부호순위검정 (Wilcoxon signed-rank test) 부호검정 (Sign test) |
| 독립된 두 집단의 차이 비교 | 독립표본 t검정 (Independent t-test) | 윌콕슨 순위합검정 (Wilcoxon rank-sum test) 맨-휘트니 U검정 (Mann-Whitney U test) |
| 독립된 3개 이상의 집단의 차이 비교 | 일원분산분석 F검정 (One-way ANOVA) | 크루스칼-왈리스 검정 (Kruskal-Wallis test) |
| 3번 이상의 반복 관측된 집단의 차이 비교 | 반복측정분산분석 F검정 (Repeated measures ANOVA) | 프리드만 검정 (Friedman test) |
| 독립된 두 집단의 범주형 변수 차이 비교 | – | 카이제곱 독립성 검정 (Chi-square test for independence) |