Z검정입니다.
Z검정과 t검정은 확률변수가 정규분포를 따르거나 표본크기가 30이상인 경우에 사용합니다.
확률변수가 정규분포를 따르지 않고 표본크기가 30미만인 경우는 비모수검정을 사용합니다.
모분산이 알려진 경우에는 표본크기와 관계없이 Z검정을 사용합니다. 모분산을 알면 모집단의 실제 변동성을 직접 반영할 수 있습니다. 따라서 자유도에 따른 보정이 필요하지 않습니다. 그러나 모분산을 아는 경우는 현실적으로 거의 없습니다. 모분산을 아는 경우는 장기간에 걸쳐 변동이 관측된 경우나 인위적으로 주어진 가우시안 노이즈인 경우가 있습니다.
모분산이 알려져 있는 경우, 우리는 모집단의 진정한 변동성을 알고 있으므로 표본의 변동성에 대한 추정치가 필요하지 않습니다. 따라서 Z검정은 모분산을 사용하여 정확한 통계량을 계산할 수 있습니다. 검정통계량이 표준 정규분포에 정확히 따르기 때문에, 작은 표본크기에서도 Z검정이 정확한 결과를 제공합니다.
Z검정 사용예: 표본평균과 모평균의 비교
확률변수($X$)가 정규분포를 따르거나 표본크기($n$)가 커서 $n \geq 30$인 경우, 표본평균($\bar X$)의 Z통계량은 다음과 같습니다.
$$Z = \dfrac{\bar{X} – \mu}{\dfrac{\sigma}{\sqrt{n}}} \sim Z(0,1)$$
여기서, $Z$는 Z통계량
$\bar{X}$는 표본평균(sample mean)
$\mu$는 모평균(population mean)
$\sigma$는 모표준편차(population standard devitation)
$n$은 표본크기
$Z(0,1)$은 평균은 0, 분산이 1인 표준정규분포
표본평균의 귀무가설에서의 Z검정통계량은 다음과 같습니다.
$$Z_{\text{test}} = \dfrac{\bar{X} – \mu_0}{\dfrac{\sigma}{\sqrt{n}}} \sim Z(0,1)$$
여기서, $Z_{\text{test}}$는 Z검정통계량
$\bar{X}$는 관측된 표본평균(observed sample mean)
$\mu_0$는 귀무가설에서의 모평균(population mean under the null hypothesis)
$\sigma$는 알고 있는 모표준편차(known population standard devitation)
$n$은 표본크기
$Z(0,1)$은 평균은 0, 분산이 1인 표준정규분포
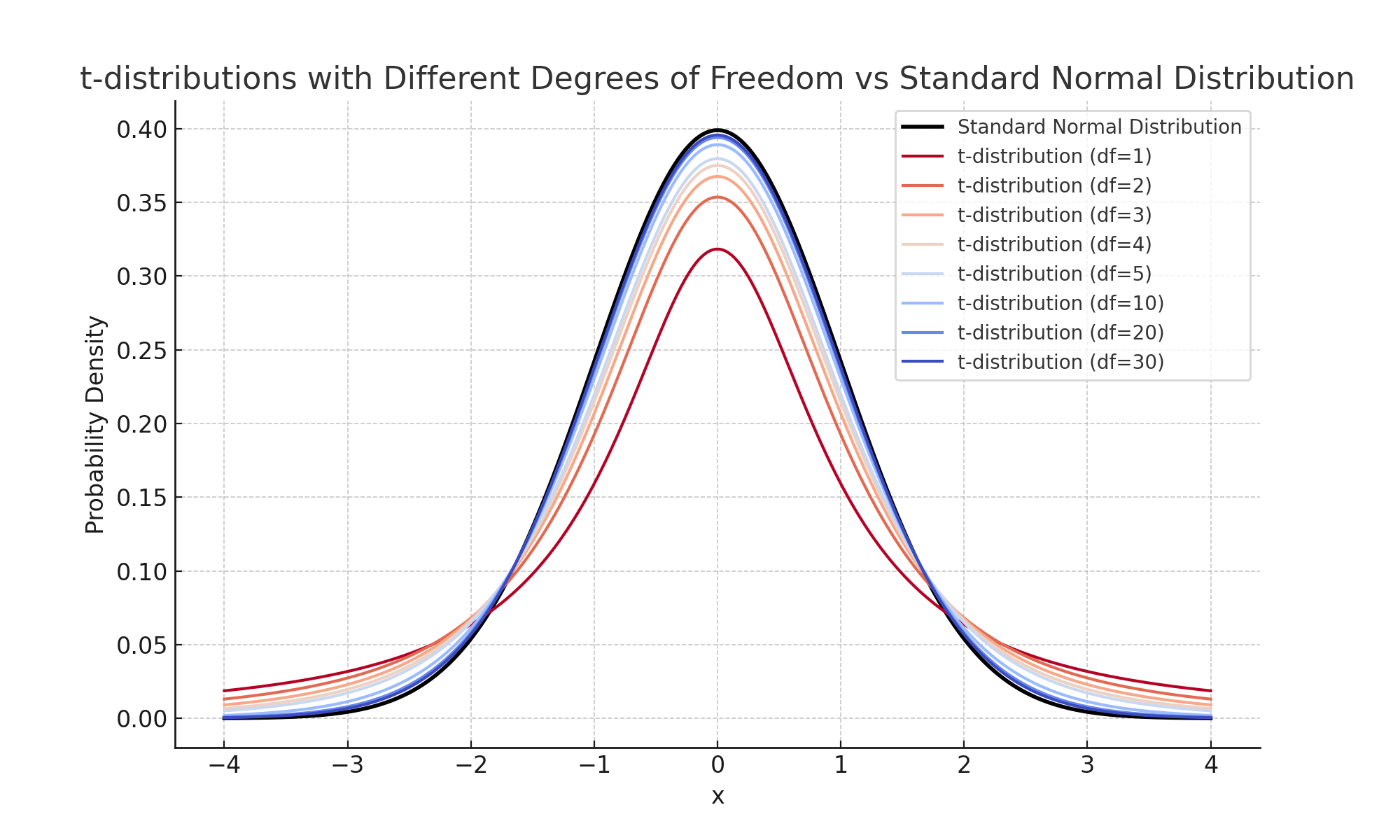
모분산을 모르는 경우, 표본크기와 관계없이 표본분산을 사용하여 t검정을 사용할 수 밖에 없습니다. 특히 작은 크기의 표본인 경우, t분포에서는 자유도에 따라 보정됩니다.
모분산을 모르는 경우, 표본분산을 사용하여 모집단의 분산을 추정할 수 밖에 없습니다. 그러나 표본분산은 표본 크기가 작을 때 모분산의 편향된 추정치가 될 수 있습니다. 이 때문에 t분포가 사용되며, 자유도에 따른 보정이 이루어집니다.
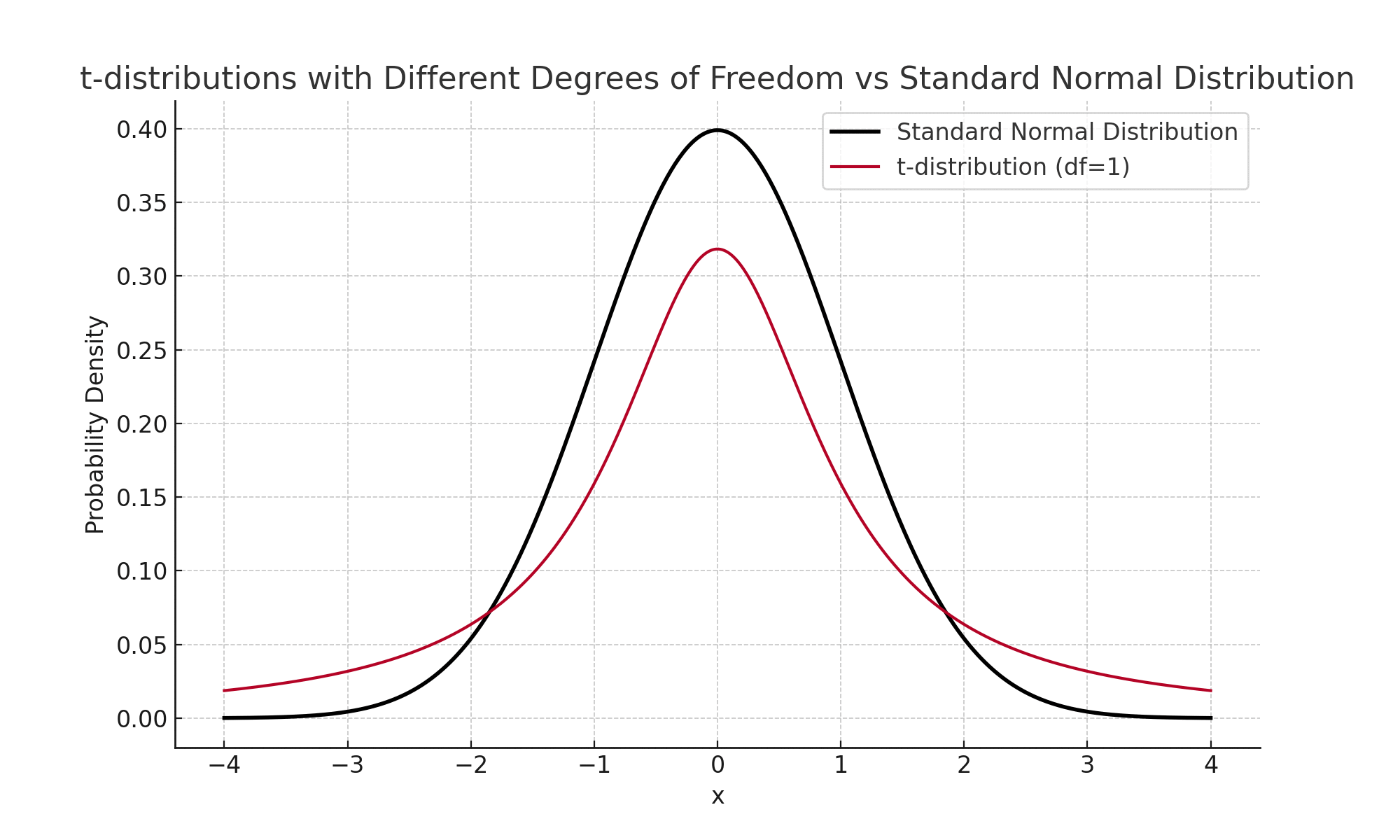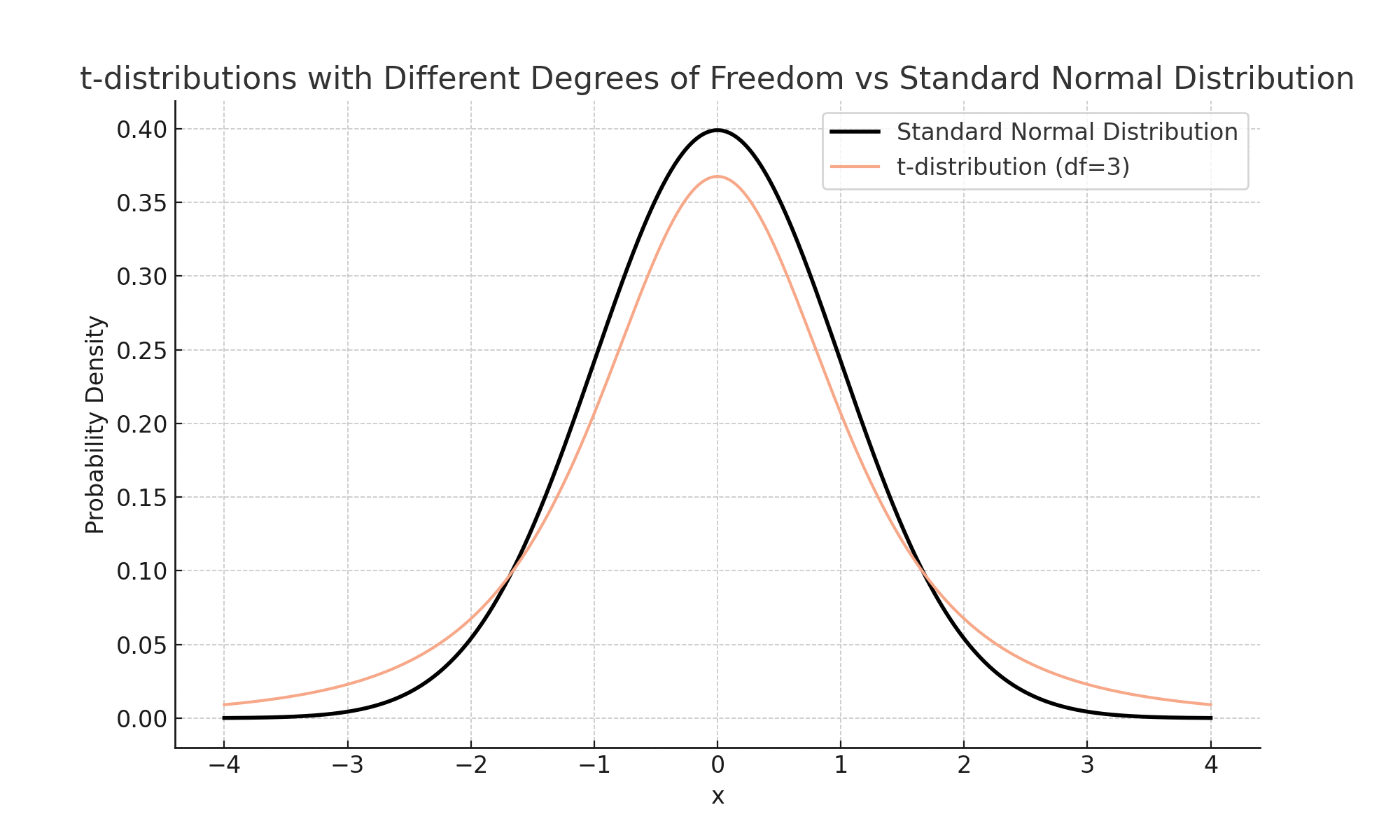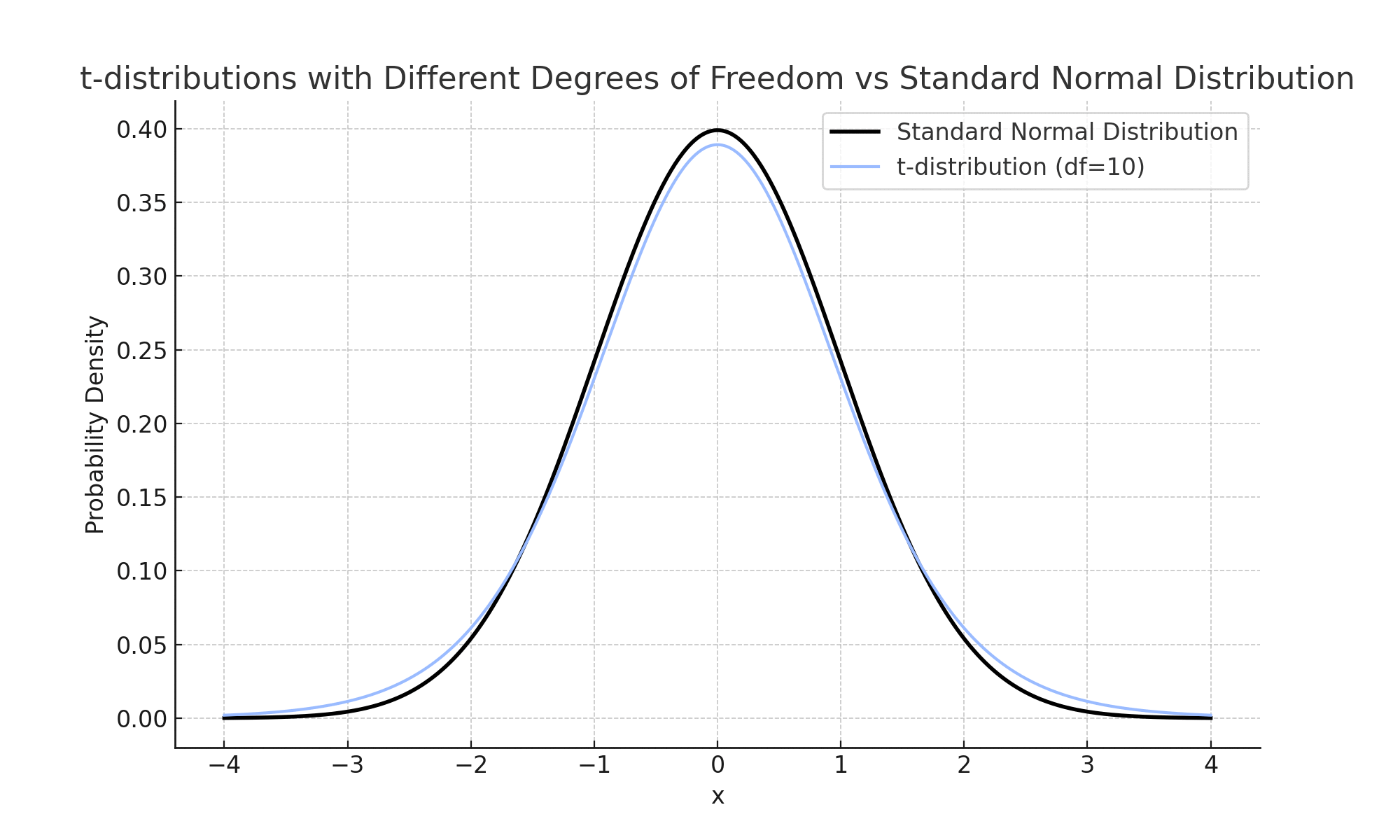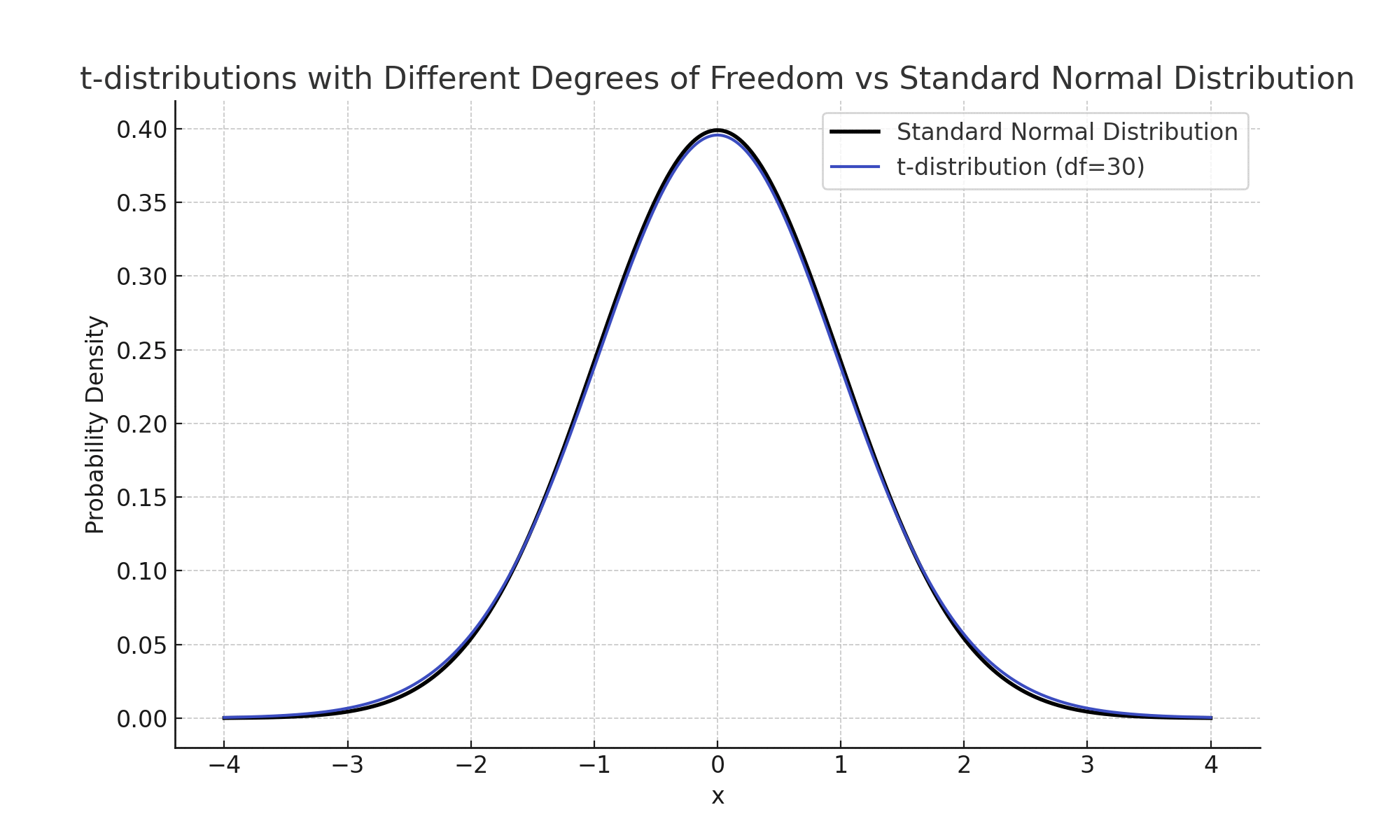
표본크기가 작을수록 t분포는 Z분포보다 꼬리가 두꺼운 형태를 나타냅니다. 이는 자유도가 낮아질수록 표본분산의 불확실성을 반영하려는 보정입니다. 따라서 t검정은 표본분산을 사용할 수밖에 없으며 특히 표본 크기가 작을 때 신뢰성을 확보하려는 방법입니다.
t검정의 사용예: 표본평균과 모평균의 비교
확률변수($X$)가 정규분포를 따르거나 표본크기($n$)가 커서 $n \geq 30$인 경우, 표본평균($\bar X$)의 t통계량은 다음과 같습니다.
$$t = \dfrac{\bar{X} – \mu}{\dfrac{s}{\sqrt{n}}}\sim t_{n-1}$$
여기서, $t$는 t통계량
$\bar{X}$는 표본평균(sample mean)
$\mu$는 모평균(population mean)
$s$는 표본표준편차(population standard devitation)
$n$은 표본크기
$n-1$은 표본의 자유도: 표본내 개체의 자유도
$t_{n-1}$은 자유도, {n-1}을 매개변수로 하는 t분포
표본평균의 귀무가설에서의 t검정통계량은 다음과 같습니다.
$$t_{\text{test}} = \dfrac{\bar{X} – \mu_0}{\dfrac{s}{\sqrt{n}}}\sim t_{n-1}$$
여기서, $t_{\text{test}}$는 t검정통계량
$\bar{X}$는 관측된 표본평균(observed sample mean)
$\mu_0$는 귀무가설에서의 모평균(population mean under the null hypothesis)
$s$는 관측된 표본표준편차(observed sample standard devitation)
$n$은 표본크기
$(n-1)$은 표본의 자유도: 표본내 개체의 자유도
$t_{n-1}$은 자유도, (n-1)을 매개변수로 하는 t분포