카이제곱은 표준정규분포에서 유도된 확률분포를 가지기 때문입니다.
표본분산을 카이제곱변환하는 과정에서 자유도의 정보가 포함됩니다.
유사하게, 표본평균을 Z변환하는 과정에서 표본크기의 정보가 포함됩니다.
확률변수의 확률분포: 정규분포로 모델링
$$Y \sim N(\mu_Y, \sigma^2_Y)$$
여기서, $Y$는 확률변수
$N(\mu_Y, \sigma^2_Y)$는 $\mu_Y$와 $\sigma^2_Y$를 매개변수로 하는 정규분포
$\mu_Y$는 확률변수 $Y$의 모평균
$\sigma^2_Y$는 확률변수 $Y$의 모분산
확률변수의 확률밀도함수
$$f_Y(x) = \frac{1}{\sqrt{2 \pi \sigma_Y^2}} \exp\left( -\frac{(x – \mu_Y)^2}{2 \sigma_Y^2} \right)$$
여기서, $f$는 정규분포의 확률밀도함수
$Y$는 확률변수
$x$는 확률밀도함수의 독립변수: $x=Y$
“Z변환된 확률변수”의 확률분포: 표준정규분포
$$\dfrac{Y-\mu_Y}{\sigma_Y} \sim N(0, 1)$$
여기서, $Y$는 정규분포를 나타내는 확률변수: $Y \sim N(\mu_Y, \sigma_Y)$
$\mu_Y$는 모평균
$\sigma_Y$는 모표준편차
모집단의 확률분포: 정규분포
$$N(\mu_Y, \sigma^2_Y)$$
여기서, $Y$는 확률변수
$N(\mu_Y, \sigma^2_Y)$는 $\mu_Y$와 $\sigma^2_Y$를 매개변수로 하는 정규분포
$\mu_Y$는 모집단의 평균
$\sigma^2_Y$는 모집단의 분산
표본의 확률분포: 정규분포
$$N(\bar Y, S^2_Y)$$
여기서, $Y$는 확률변수
$N(\bar Y, S^2_Y$)$는 $\bar Y$와 $S^2_Y$$를 매개변수로 하는 정규분포
$\bar Y$는 표본의 평균
$S^2_Y$는 표본의 분산
표본평균은 표본통계량이고 확률변수입니다.
$$\bar Y = \dfrac{1}{n} \sum_{i=1}^{n} (Y_i – \mu_Y)$$
여기서, $n$은 표본크기
$Y_i$는 $i$번째 확률변수값
$\mu_Y$는 모평균
표본크기가 무한대일 때 표본평균
$$\bar Y \xrightarrow{n \to \infty} \mu_Y$$
여기서, $\mu_Y$는 모평균
표본평균의 표집분포(sampling distribution): 정규분포
$$\bar Y \sim N \left(\mu_Y, \dfrac{\sigma^2_Y}{n} \right)$$
여기서, $\bar Y$는 표본평균
$N \left(\mu_Y, \dfrac{\sigma^2_Y}{n} \right)$은 $\mu_Y$와 $\dfrac{\sigma^2_Y}{n}$를 매개변수로 하는 정규분포
$\mu_Y$는 모평균
$\sigma^2_Y$는 모분산
$n$은 표본크기
표본평균의 확률밀도함수(PDF)
$$f_{\bar{Y}}(x) = \frac{1}{\sqrt{2\pi \frac{\sigma_Y^2}{n}}} \exp\left( -\frac{(x – \mu_Y)^2}{2 \frac{\sigma_Y^2}{n}} \right)$$
여기서, $f$는 정규분포의 확률밀도함수
$\bar Y$는 표본평균
$x$는 확률밀도함수의 독립변수: $x=\bar Y$
$\bar Y$는 표본평균: $x=\bar Y$
$\mu_Y$는 모평균
$\sigma_Y^2$은 모분산
$n$은 표본크기
Z변환된 표본평균의 표집분포(sampling distribution): 표준정규분포
$$\dfrac{\bar Y – \mu_Y}{\left(\dfrac{\sigma_Y}{\sqrt{n}}\right)}=\dfrac{\sqrt{n}(\bar Y – \mu_Y)}{\sigma_Y} \sim N(0,1)$$
여기서, $\sigma_Y$는 모표준편차
$n$은 표본크기
$N(0, 1)$은 표준정규분포
t변환된 표본평균의 표집분포(sampling distribution): t분포
$$\dfrac{\bar Y – \mu_Y}{\left(\dfrac{S_Y}{\sqrt{n}}\right)}=\dfrac{\sqrt{n}(\bar Y – \mu_Y)}{S_Y} \sim t_{n-1}$$
여기서, $S_Y$는 표본표준편차
$n$은 표본크기
$t_{n-1}$은 자유도가 $(n-1)$인 스튜던트 t분포
표본분산은 표본통계량이고 확률변수입니다. 표본분산을 다음과 같이 표현할 수 있습니다.
$$S_Y^2 = \dfrac{1}{n-1} \sum_{i=1}^{n} (Y_i – \bar{Y})^2$$
여기서, $n$은 표본크기
$Y_i$는 $i$번째 확률변수값
$\bar Y$는 표본평균
표본크기가 무한대일 때 표본분산
$$S_Y^2 \xrightarrow{n \to \infty} \sigma_Y^2$$
여기서, $\sigma^2_Y$는 모분산
표본분산의 표집분포(sampling distribution)
$$S_Y^2 \sim \text{Gamma}\left(\frac{n-1}{2}, \frac{2\sigma^2}{n-1}\right)$$
여기서, $n$은 표본크기
$\sigma_Y^2$은 모분산
$\frac{n-1}{2}$는 모양 매개변수
$\frac{2\sigma_Y^2}{n-1}$은 스케일 매개변수
표분분산의 확률밀도함수(PDF)
$$f_{S_Y^2}(x) = \frac{1}{\Gamma\left(\frac{n-1}{2}\right)} \left(\frac{n-1}{2\sigma_Y^2}\right)^{\frac{n-1}{2}} x^{\frac{n-1}{2} – 1} e^{-\frac{(n-1)x}{2\sigma_Y^2}}, \quad x > 0$$
여기서, $\Gamma( \,\,)$는 감마함수
$S_Y^2$은 표본분산
$x$는 감마함수의 독립변수: $x=S_Y^2$
$\frac{n-1}{2}$는 자유도와 관련된 매개변수
$\sigma_Y^2$는 모분산
카이제곱은 다음과 같이 정의됩니다.
$$\chi^2 = \sum_{i=1}^{k} Z_i^2$$
여기서, $\chi^2$은 카이제곱분포를 가지는 확률변수
$k$는 자유도
$Z_i$는 $i$번째 표준정규분포를 나타내는 확률변수
카이제곱변환된 표본분산의 표집분포: 카이제곱분포.
$$\dfrac{(n-1)S_Y^2}{\sigma_Y^2} \sim \chi^2_{n-1} \sim \text{Gamma} \left(\dfrac{n-1}{2}, 2 \right)$$
여기서, $n$은 표본크기
$(n-1)$은 표본의 자유도
$S_Y^2$은 확률변수 $Y$의 표본분산
$Y$는 확률변수이며 정규분포를 나타냄: $Y\sim N(\mu, \sigma_Y^2)$
$\sigma_Y^2$은 확률변수 $Y$의 모분산
$\chi^2_{n-1}$은 자유도 $(n-1)$인 카이제곱분포
$\Gamma \left(\dfrac{n-1}{2}, 2 \right)$는 매개변수가 $\dfrac{n-1}{2}$와 $2$인 감마함수
카이제곱분포의 확률밀도함수
$$f(x; k) = \dfrac{1}{2^{k/2} \Gamma(k/2)} x^{(k/2)-1} e^{-x/2} \quad \text{for} \quad x > 0$$
여기서, $f$는 확률밀도함수
$x$는 카이제곱분포를 나타내는 확률변수: $x \sim \chi^2$
$k$는 자유도
$\Gamma(k/2)$는 감마함수: $\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \quad \text{for} \quad \text{Re}(z) > 0$, $z$는 복소수
표본크기가 무한대일 때 카이제곱분포
$$\chi^2_k \xrightarrow{n \to \infty} N(k, 2k)$$
여기서, $n$은 표본크기
$k$는 표본내 개체의 자유도: $k=n-1$
“모분산으로 표준화된 표본분산”의 표집분포
$$ \dfrac{S^2_Y}{\sigma^2_Y} \sim \text{Gamma}\left(\frac{n-1}{2}, \frac{2}{n-1}\right)$$
여기서, $S_Y^2$은 확률변수 $Y$의 표본분산
$Y$는 정규분포를 나타내는 확률변수: $Y\sim N(\mu, \sigma_Y^2)$
$\sigma_Y^2$은 모분산
$\chi^2_{n-1}$은 자유도 $(n-1)$인 카이제곱분포
$\text{Gamma}\left(\frac{n-1}{2}, \frac{2}{n-1}\right)$는 매개변수가 $\frac{n-1}{2}$와 $ \frac{2}{n-1}$인 감마분포
“모분산으로 표준화한 표본분산”의 확률밀도함수
$$f\left(\frac{x}{k}; k\right) = \frac{1}{2^{k/2} \Gamma(k/2)} \left( \frac{x}{k} \right)^{(k/2 – 1)} e^{-\frac{x}{2k}}, \quad x > 0$$
여기서, $f(\frac{x}{k}; k)$은 자유도가 $k$인 카이제곱분포의 확률밀도함수
$x$는 확률변수: $x = \frac{S_Y^2}{\sigma_Y^2}$
$k$는 자유도
$\Gamma(k/2)$는 감마함수: $\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \quad \text{for} \quad \text{Re}(z) > 0$, $z$는 복소수
표본크기가 무한대일 때 모분산으로 표준화한 표본분산의 수렴값
$$\dfrac{S_Y^2}{\sigma_Y^2} \xrightarrow{n \to \infty} 1 $$
$S_Y^2$는 표본분산
$\sigma^2_Y$는 모분산
F통계량은 두 표본분산의 F변환된 확률변수입니다.
두 표본분산의 F의 변환식은 다음과 같습니다. 단, 모집단이 정규분포여야 합니다. 즉, 확률변수가 정규분포를 나타내야 합니다.
$$F = \dfrac{\left( \dfrac{S_1^2}{\sigma_1^2} \right)}{\left( \dfrac{S_2^2}{\sigma_2^2} \right)} = \dfrac{\dfrac{S_1^2}{\sigma_1^2}}{\dfrac{S_2^2}{\sigma_2^2}} \sim F_{\nu_1,\nu_2}$$
$S^2_1$과 $S^2_2$는 두 개의 독립적인 표본에서 계산된 표본분산
$\sigma^2_1$과 $\sigma^2_2$는 각각의 모집단 분산
$\nu_1$과 $\nu_2$는 각각 두 표본의 자유도: $\nu_1=n_1-1$, $\nu_2=n_2-1$
$n_1$과 $n_2$은 각각 두 표본의 크기
F분포의 확률밀도함수는 다음과 같습니다.
$$f(x; d_1, d_2) = \frac{\left( \frac{d_1}{d_2} \right)^{d_1/2} x^{d_1/2 – 1}}{B\left( \frac{d_1}{2}, \frac{d_2}{2} \right) \left( 1 + \frac{d_1}{d_2} x \right)^{(d_1 + d_2)/2}}, \quad x > 0$$
여기서, $B(a, b)$는 베타함수: $B(a, b) = \frac{\Gamma(a) \Gamma(b)}{\Gamma(a + b)}$
$k$는 자유도
$\Gamma(k/2)$는 감마함수: $\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \quad \text{for} \quad \text{Re}(z) > 0$, $z$는 복소
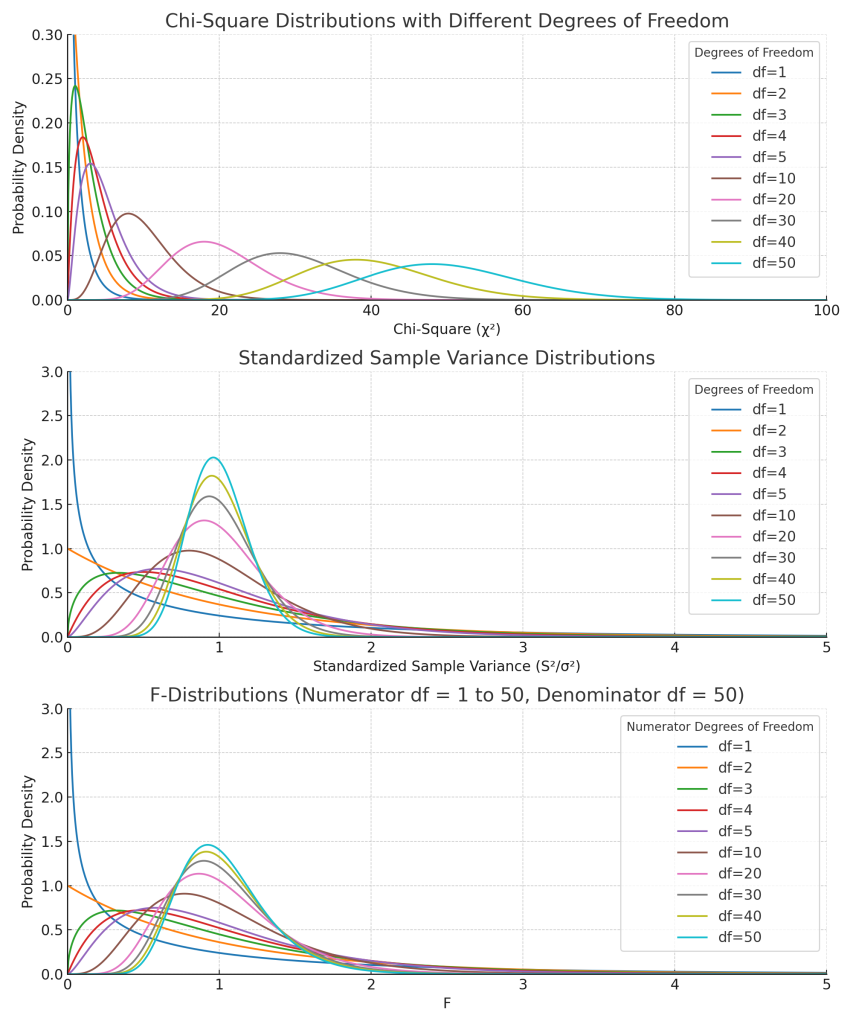
모분산 추정
모집단의 분산에 대한 신뢰구간을 설정할 때 카이제곱변환을 사용합니다. 표본분산을 카이제곱변환하면 주어진 신뢰수준에서 정확한 신뢰구간을 계산할 수 있습니다.
분산 검정
모분산이 특정 값과 다른지를 검정할 때, 표본분산을 카이제곱변환하여 카이제곱검정을 수행합니다. 이때, 카이제곱분포는 검정통계량의 분포를 제공하므로, 표본분산보다 더 직접적으로 검정에 활용될 수 있습니다.
분산분석(ANOVA) F검정
F변환을 사용하여 독립적인 집단의 두 표본분산을 F변환하여 F통계량을 구합니다. 분산분석(ANOVA)에서는 집단간분산과 집단내분산의 비를 검정할 때 F통계량을 사용합니다.