최대우도법은 주어진 데이터로 모델하는 확률분포의 모수를 계산하는 방법론입니다.
최대우도법(Maximum Likelihood Method)을 통해 최대가능도추정량이 도출됩니다.
최대가능도추정량(Maximum Likelihood Estimator, MLE)은 추출한 표본데이터에서 우도(가능도)를 최대로 하는 모수의 추정량을 나타내는 수식입니다.
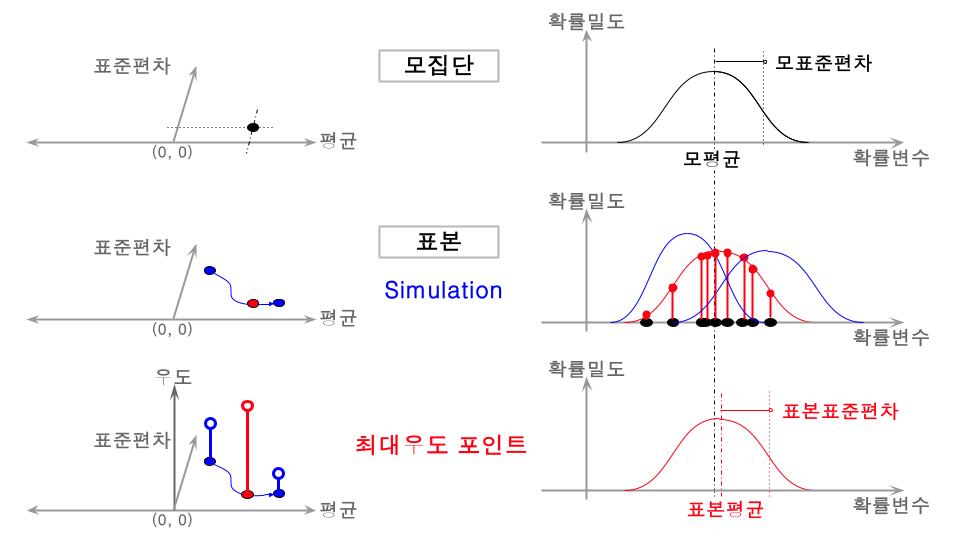
최대우도법(Maximum Likelihood Method, MLM)은 주어진 데이터를 가장 잘 설명하는 확률분포의 모수(parameter)를 점추정하는 방법론입니다. 최대우도법에서는 우도함수(likelihood function) $L$을 최대화하는 모수 값 $\hat {\theta_{MLE}}$을 최적화 알고리즘으로 찾습니다. 최적화 알고리즘에는 뉴턴-랩슨방법(Newton-Rapson Method), 경사하강법(Gradient Descent) 등이 있습니다. 우도함수는 주어진 데이터 $X$가 특정 모수 $\theta$에서 나올 확률을 의미합니다.
최대우도추정량(Maximum Likelihood Estimator, MLE)은 최대우도법을 적용하여 도출된 결과이며 다음식으로 표현됩니다. 최대우도추정량은 관측된 데이터 $x_i$로 $X$를 고정하고 $\theta$를 변화시키면서 우도함수(尤度函數)에 대입하며 최대가 되는 우도함수값 $\theta$를 찾는 수식표현입니다.
$$\hat{\theta}_{\text{MLE}} = \arg\max_{\theta} L(\theta \mid X)=\arg\max_{\theta} P(X \mid \theta)
$$
여기서, $L(\theta|X)$는 데이터 $X$에서 모수 $\theta$가 주어졌을 때의 우도함수(likelihood fuction)
P($X \mid \theta$)는 모수 $\theta$ 조건에서의 확률변수 $X$의 조건부확률분포함수
전체 표본의 우도함수는 개별 데이터($x_i$)에서의 확률밀도(또는 확률질량)의 곱으로 표현됩니다. 표본의 우도함수는 표본원소가 서로 독립이라는 가정하에 표본원소의 우도함수를 모두 곱한 함수입니다. 한 표본원소의 우도는 단일 관측값이 주어졌을 때의 우도함수입니다. 연속형 확률변수일때는 확률밀도함수 $f(x|\theta)$로 표현되며 이산형 확률변수에서는 확률질량함수 $P(x|\theta)$로 표현됩니다. 다음식은 표본크기가 $n$인 전체 표본의 우도함수를 표현한 식입니다.
\[
L(\theta \mid X) = \prod_{i=1}^n f(x_i \mid \theta)
\]
여기서, $L(\theta \mid X)$는 표본의 우도함수
$f(x_i \mid \theta)$는 개별 데이터 $x_i$의 우도함수이며 확률밀도함수 또는 확률질량함수
$n$은 관측된 데이터 수
우도(尤度)는 한국과 일본에서 “Likelihood”와 같은 의미로 쓰는 용어입니다. 尤(우)는 “더할 나위 없이” 또는 “특히”라는 의미를 지니며. 度(도)는 “정도”, “측정”의 의미를 갖습니다. 우도는 가능도(可能度)로 대체하여 사용하기도 합니다.
중국에서는 우도 대신에 시연(似然)이라는 용어를 사용합니다.