평균은 위치이고 분산은 양이며, 평균의 비교는 t검정으로 분산의 비교는 F검정으로 행합니다.
위치(位置, position)를 다루는 학문은 기원전 3000년경에 시작된 기하학(geometry)입니다. 양(量, quantity)을 다루는 학문은 기원전 2000년경 이후 성립된 산술(arithmetic)입니다.
이산형(discrete type) 데이터인 경우에도 평균/분산이라는 모수 개념이 성립하지만, 본질적으로 연속형(continuous type) 데이터에서 의미가 명확합니다. 연속형 데이터인 경우에 “평균”, “분산” 이라는 모수(parameter)를 부여하는 것이 더 자연스럽습니다.
위치를 평균(mean)으로 양을 분산(variance)으로 적용하면,
평균(위치)을 비교할 때 → t검정
분산(양)을 비교할 때 → F검정
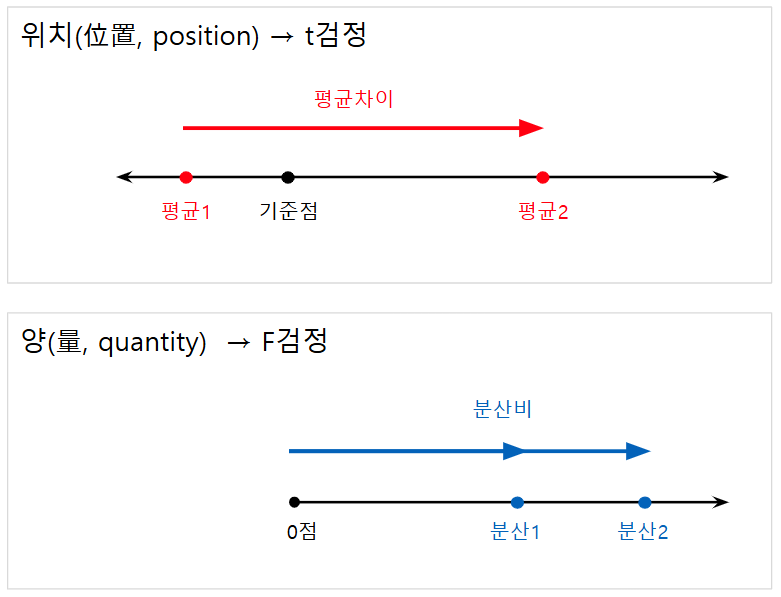
Fig. 1. 위치 또는 양을 검정
Table 1. 위치와 양의 가설검정
| 항목 | 위치 (이산) | 위치 (연속) | 양 (이산) | 양 (연속) |
|---|---|---|---|---|
| 성질 | 이산 (discrete) | 연속 (continuous) | 이산 (discrete) | 연속 (continuous) |
| 수 체계 | $\mathbb{Z}$ | $\mathbb{R}$ | $\mathbb{N}$, $\mathbb{Z}$ | $\mathbb{R}_{\geq 0}$ |
| 설명 | 수직선 위 정수 위치 | 수직선 위 연속 위치 | 셀 수 있는 개수의 변동성 | 연속적인 양의 변동성 |
| 비교 기준 항등원 | $0$ (기준점) | $0$ (기준점) | $0$ | $0$ |
| 비교 방법 (사칙연산) | 차이 ($-$) | 차이 ($-$) | 비율 ($\div$) | 비율 ($\div$) |
| “두 값이 같다” 가설 수식 | $\mu_1 – \mu_2 = 0$ | $\mu_1 – \mu_2 = 0$ | $\dfrac{\sigma_1^2}{\sigma_2^2} = 1$ | $\dfrac{\sigma_1^2}{\sigma_2^2} = 1$ |
| 영가설 ($H_0$) | $H_0: \mu_1 – \mu_2 = 0$ | $H_0: \mu_1 – \mu_2 = 0$ | $H_0: \sigma_1^2 = \sigma_2^2$ | $H_0: \sigma_1^2 = \sigma_2^2$ |
| 대립가설 ($H_1$) | $H_1: \mu_1 – \mu_2 \neq 0$ | $H_1: \mu_1 – \mu_2 \neq 0$ | $H_1: \sigma_1^2 \neq \sigma_2^2$ | $H_1: \sigma_1^2 \neq \sigma_2^2$ |
| 모수에의 적용 | – | 평균 (mean) | – | 분산 (variance) |
| 적용되는 검정 | 1표본/2표본 $t$-검정 | 1표본/2표본 $t$-검정 | 2표본 $F$-검정 | 2표본 $F$-검정 |
| 검정통계량 식 | $t = \dfrac{\bar{x}_1 – \bar{x}_2}{\sqrt{s_p^2\left(\dfrac{1}{n_1} + \dfrac{1}{n_2}\right)}}$ (단, $s_p^2 = \dfrac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}$) |
$t = \dfrac{\bar{x}_1 – \bar{x}_2}{\sqrt{s_p^2\left(\dfrac{1}{n_1} + \dfrac{1}{n_2}\right)}}$ (단, $s_p^2 = \dfrac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}$) |
$F = \dfrac{s_1^2}{s_2^2}$ | $F = \dfrac{s_1^2}{s_2^2}$ |
Table 2. t검정 비교
| 구분 | 1표본 t-검정 | 2표본 t-검정 |
|---|---|---|
| 비교 대상 | 하나의 표본 평균과 특정 값(모평균)을 비교 | 두 표본 평균 간 차이를 비교 |
| 사용 상황 | 한 집단의 평균이 기준값과 같은지 검정 | 두 집단의 평균이 서로 다른지 검정 |
| 예시 | “학생들의 평균 키가 160cm인가?” | “남학생과 여학생의 평균 키가 같은가?” |
| 표본 수 | 1개 ($n$) | 2개 ($n_1$, $n_2$) |
| 검정통계량 | $t = \dfrac{\bar{x} – \mu_0}{s/\sqrt{n}}$ | $t = \dfrac{\bar{x}_1 – \bar{x}_2}{\sqrt{s_p^2\left(\dfrac{1}{n_1} + \dfrac{1}{n_2}\right)}}$ (단, $s_p^2 = \dfrac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}$) |
| 기본 가정 | 표본은 정규분포, 독립적 표본 | 두 표본은 독립적, 각각 정규분포 |
| 모수에의 적용 | 모평균 $\mu$ | 두 모평균 $\mu_1$, $\mu_2$ |
비율검정(proportion test) 은 양인 “비율”을 다루는 검정이지만 검정통계량을 계산할 때는 **비율 간의 차이(difference)**를 이용합니다. 즉, “비율” 자체를 비교하는 것이 목적이지만 실제 검정에서는 비율 간 차이를 통계량으로 삼습니다.
비율검정은 “어떤 집단에서 특정한 성질을 가진 비율이 예상(기대)한 비율과 같은지”를 검정하는 방법입니다.
비율검정은 “비율이 특정 값과 같은지” 또는두 집단의 비율이 같은지”를 검정합니다.
주로, 성공률/불량률/투표율 등 “비율”을 다룰 때 사용합니다. 핵심은 “비율(확률)” 을 비교한다는 것입니다.
1표본 비율검정은 한 집단의 비율이 특정 비율과 같은지를 검정합니다.
– 제품 불량률이 5%라고 주장할 때
– 새 백신의 예방률이 95%라고 주장할 때
– 학생 중 남학생 비율이 50%라고 주장할 때
1표본 비율검정은 주장하는 비율이 맞는지 표본(sample)만 보고 모집단(population)의 비율을 추정하여 통계적으로 확인합니다.
2표본 비율검정은 두 집단의 비율이 서로 같은지를 검정합니다.
– A백신과 B백신의 예방률이 같다고 주장할 때
2표본 비율검정은 주장하는 비율이 맞는지 2표본(sample)을 보고 두 모집단(population)의 비율을 추정하여 통계적으로 확인합니다.
비율검정은 표본이 우연인지, 정말 비율이 다른 것인지를 통계적으로 확인합니다.
1표본 비율검정 (one-sample proportion test)
– 비교하는 것은 표본 비율 $\hat{p}$과 가설 비율 $p_0$
– 검정통계량 표본 비율과 가설 비율의 차이(difference)를 이용
$$z = \frac{\hat{p} – p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}$$
2표본 비율검정 (two-sample proportion test)
– 비교하는 것은 두 표본 비율 $\hat{p}_1$과 $\hat{p}_2$
– 검정통계량 두 표본 비율의 차이(difference)를 이용
$$z = \frac{\hat{p}_1 – \hat{p}_2}{\sqrt{p(1-p)\left(\dfrac{1}{n_1} + \dfrac{1}{n_2}\right)}}
$$
여기서, $p$는 두 표본을 합쳐서 계산한 합동 비율
비율은 양입니다. 두 비율의 비를 검정하는 귀무가설은 다음과 같습니다.
$$\dfrac{\hat{p}_1}{\hat{p}_2} = 1$$
두 비율을 양으로 비교하여 비를 살펴보면 분모인 $\hat{p}_2$의 값이 0에 가까운 경우, 비가 급격히 커져서 안정적인 검정이 어렵습니다.
$$\hat{p}_2 \approx 0 \quad \Rightarrow \quad \text{비율 발산 (unstable)}$$
따라서, 비율검정에서는 일부러 “차이”를 사용합니다. 차이(difference)를 비교하면 값이 작을 때나 클 때나 양쪽으로 대칭적이고 표준오차 계산이 쉬워서 검정 절차가 수학적으로 훨씬 안정적입니다.
$$ \hat{p}_1 – \hat{p}_2 = 0$$
반면, 차이(difference)는 $\hat{p}_1 – \hat{p}_2 = 0$을 기준으로 값이 항상 $-1$에서 $+1$ 사이에 존재하고 대칭적인 분포를 가지며 표준 정규분포로 근사하기 쉽습니다. 수학적으로 보면, 비율(ratio)은 scale-invariant(배율 불변) 특성을 가지지만 검정에서는 location-invariant(위치 불변) 특성이 훨씬 유리합니다. 차이(difference)는 “위치”를 비교하는 것이므로 귀무가설($H_0$)을 “차이 = 0″으로 세우기 쉽고, 안정적입니다.

Fig. 2. 차이와 비로 두 비율을 비