DATA SCIENCE : 27
DATA SCIENCE eISSN
네, 정규분포의 표본평균과 표본분산은 확률변수이고 독립입니다.
정규분포 $\mathcal{N}(\mu, \sigma^2)$ 에서 추출된 모든 $n \geq 2$의 표본에서 표본평균($ \bar{X}$)과 표본분산$(S^2)$은 독립입니다.
$$\bar{X} \perp S^2$$
표본의 평균과 분산이 독립이라는 것은 어느 표본의 평균값을 알아도 분산값을 예측할 수 없고 반대도 마찬가지라는 것입니다.
정규분포 $X \sim \mathcal{N}(\mu, \sigma^2)$의 확률밀도함수는 다음식으로 표현됩니다.
$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{(x – \mu)^2}{2\sigma^2} \right), \quad x \in \mathbb{R}$$
여기서, $x$는 확률변수이며 실수 수체계를 가짐
$\mu$는 평균: 분포의 중심위치
$\sigma^2$은 분산: 분포의 퍼짐 정도
Table 1. 정규분포의 성질
| 성질 | 설명 |
|---|---|
| 평균 = 중앙값 = 최빈값 | 중심이 모두 동일한 값 $\mu$ |
| 대칭성 | $x = \mu$를 기준으로 완벽히 대칭 |
| 선형성 보존 | 어떤 확률변수 $X$가 정규분포를 따른다면, $aX+b$와 같 선형변환한 결과도 역시 정규분포를 따름 $aX + b \sim \mathcal{N}(a\mu + b, a^2\sigma^2)$ |
| 표본평균 분포 | $\bar{X} \sim \mathcal{N}(\mu, \sigma^2/n)$ |
| 표본평균과 분산 독립 | $\bar{X} \perp S^2$ (정규분포만 가짐) |
| 정규분포의 합도 정규 | $X_1 + X_2 \sim \mathcal{N}(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$ |
| 표준정규변환 | $Z = \frac{X – \mu}{\sigma} \sim \mathcal{N}(0, 1)$ |
다변량 정규분포도 선형결합, 조건부분포, 주변분포가 정규분포 형태를 유지합니다.
$$\mathbf{X} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$$
여기서, $\boldsymbol{\mu}$는 평균벡터
$\boldsymbol{\Sigma}$는 공분산 행렬
다변량 정규분포(multivariate normal distribution)로의 확장이 가능한 이유는 다음과 같습니다.
1. 선형결합이 정규분포를 유지
$$\mathbf{X} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma}) \Rightarrow a^\top \mathbf{X} \sim \mathcal{N}(a^\top \boldsymbol{\mu}, a^\top \boldsymbol{\Sigma} a)$$
정규분포는 선형변환에 닫혀 있으므로, 고차원에서도 잘 정의됨
2. 이차형식이 자연스럽게 확장가능
단변량 정규분포의 밀도함수:
$$f(x) \propto \exp\left( -\frac{1}{2\sigma^2} (x – \mu)^2 \right)$$
다변량 정규분포는 다음과 같은 이차형식으로 일반화:
$$f(\mathbf{x}) \propto \exp\left( -\frac{1}{2} (\mathbf{x} – \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\mathbf{x} – \boldsymbol{\mu}) \right)$$
이차형식은 선형대수적으로 정의 가능하며, 회전·축척·이동 모두 수학적으로 다룰 수 있음
3. 공분산 행렬의 양의 정부호 성질
4. 지수족 구조 유지
5. 회전불변성과 구면 대칭성
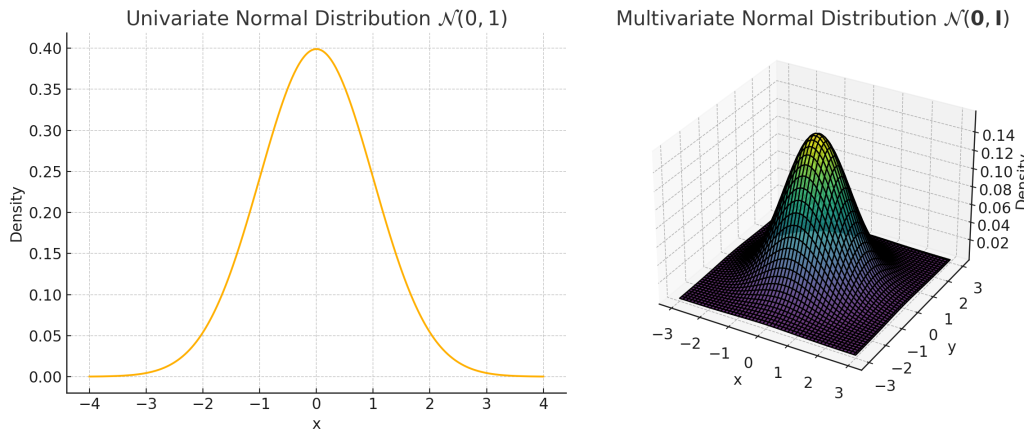
Fig. 1. 단변량 및 다변량 정규분포 시각화