네. 절편(intercept) 뿐만 아니라 기울기(slope)에도 영향을 줄 수 있습니다.
절편에 랜덤효과가 더해지면 각 집단의 회귀선이 평행이동합니다. : 랜덤절편모델 (Random intercept model)
기울기에 랜덤효과가 더해지면 각 집단의 회귀선이 회전합니다. : 랜덤기울기모델 (Random slope model)
절편과 기울기, 동시에 랜덤효과가 더해지면 각 집단의 회귀선의 절편과 기울기가 모두 달라집니다. : 랜덤절편기울기모델 (Random intercept and slope model)
랜덤절편모델 (Random intercept model)에서는 집단 $j$마다 절편만 달라지고, 기울기는 공통이기 때문에 각 집단의 회귀선은 평행합니다.
랜덤절편모델은 종속변수의 벡터를 집단에 공통된 고정효과($\beta_0, \beta_1$)와 집단마다 다른 랜덤 절편($u_{0j}$와 개체마다 다른 잔차 변동($\epsilon_{ij}$로 표현합니다.
\[
Y_{ij} \;=\; \beta_0 + u_{0j} + \beta_1 X_{ij} + \varepsilon_{ij},
\quad \operatorname{E}[u_{0j}] = 0,\;
\operatorname{Var}(u_{0j}) = \sigma_{u0}^2,\;
\varepsilon_{ij} \sim \mathcal{N}(0,\sigma_e^2)
\]
여기서, $Y_{ij}$는 $j$번째 집단에 속한 $i$번째 개체의 관측값(반응값): 예 학교의 학생의 시험점수, 목장의 소의 체중
$\beta_0$는 전체평균(절편, intercepti): 모든 집단에 적용되는 기저수준
$\beta_1$는 설명변수 $X_{ij}$에 대한 공통기울기
$X_{ij}$는 $j$번째 집단의 $i$번째 개체의 설명변수값: 예, 학생의 공부시간, 소의 연령
$u_{0j}$는 $j$번째 집단의 절편 (randdom intercept): 예 학교별 평균차이, 목장별 평균차이
$\epsilon_{ij}$는 개체수준의 잔차: 예 집단내에서 개체별 변동
PBLUP/GBLUP의 혼합선형모델은 “랜덤절편모델”입니다.
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z} \mathbf{u} + \mathbf{e},
\quad \mathbf{u} \sim \mathcal{N}\!\left(0, \sigma^2 \mathbf{A}\right) \; (\text{PBLUP}),
\quad \mathbf{u} \sim \mathcal{N}\!\left(0, \sigma^2 \mathbf{G}\right) \; (\text{GBLUP})
\]
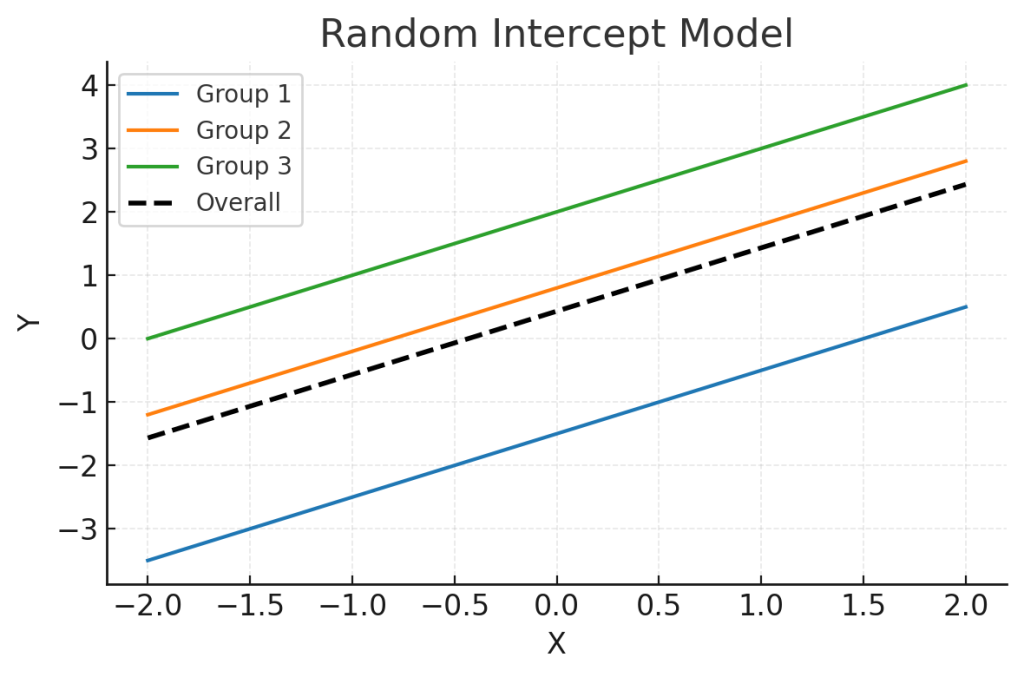
Fig. 1. 랜덤절편모델 (Random Intercept Model)
랜덤기울기모델 (Random intercept model)에서는 집단 $j$마다 기울기만 달라지고, 절편은 공통이기 때문에 각 집단의 회귀선은 평행하지 않고 전체절편을 중심으로 회전합니다.
이 모델은 “어떤 공변량 $W$”에 대해서 집단별로 반응 기울기가 다르다는 것을 허용합니다. 예를 들어 교육 연구에서는 “공부시간($W$)이 성적($Y$)에 미치는 효과가 학교마다 다르다.”가 있고, 유전육종학에서는 “온도 스트레스 지수(THI, $W$)가 산유량($Y$)에 미치는 민감도가 목장마다 다르다.”가 있습니다.
랜덤 기울기 모델은 종속변수의 벡터를 집단에 공통된 고정효과($\beta_0, \beta_1$)와 집단마다 다른 기울기($u_{1j}$와 개체마다 다른 잔차 변동($\epsilon_{ij}$로 표현합니다.
공변량 $W_{ij}$대한 집단별 기울기를 허용하며 실무에서는 $W$를 센터링($\widetilde{W} = W – \overline{W}$)하여 식별성과 해석력을 높입니다. 즉, 센터 기준점에서 절편과 기울기를 분리합니다.
\[
Y_{ij} = \beta_0 + \beta_1 X_{ij} + (\beta_W + u_{1j}) W_{ij} + \varepsilon_{ij},
\quad \operatorname{E}[u_{1j}] = 0,\;
\operatorname{Var}(u_{1j}) = \sigma_{u1}^2
\]
여기서, $Y_{ij}$는 $j$번째 집단에 속한 $i$번째 개체의 관측값(반응값): 예 학교의 학생의 시험점수, 목장의 소의 체중
$\beta_0$는 전체평균(절편, intercepti): 모든 집단에 적용되는 기저수준
$\beta_1$는 설명변수 $X_{ij}$에 대한 공통기울기
$\beta_W$는 설명변수 $W_{ij}$에 대한 공통기울기(평균적 효과)
$X_{ij}$는 $j$번째 집단의 $i$번째 개체의 설명변수값: 예, 학생의 공부시간, 소의 연령
$W_{ij}$는 $j$번째 집단의 $i$번째 개체의 집단마다 다른 랜덤 기울기를 허용하는 공변량(설명변수값): 예, 학생의 민감도, 소의 민감도
$u_{1j}$는 $j$번째 집단의 기울기 (randdom slope): 예 학교별 민감도, 목장별 민감도
$\epsilon_{ij}$는 개체수준의 잔차: 예 집단내에서 개체별 변동
유전평가에서의 예로는 반응규범(Reactin norm) PBLUP/GBLUP가 있습니다. 환경지표(THI=온열스트레스지수, 사료에너지 수준, 고도 등)를 $W$로 두고 개체별 민감도(기울기)를 랜덤화 합니다.
\[
\mathbf{y} = \mathbf{X}\boldsymbol{\beta}
+ \mathbf{Z} \mathbf{u}
+ \mathbf{Z}_b (\mathbf{b} \odot \widetilde{\mathbf{W}})
+ \mathbf{e}
\]
\[
\begin{bmatrix}
\mathbf{a} \\
\mathbf{b}
\end{bmatrix}
\sim \mathcal{N}\!\left(
\mathbf{0},\;
\begin{bmatrix}
\sigma_u^2 \mathbf{u} & \sigma_{ub}\mathbf{A} \\
\sigma_{ub}\mathbf{A} & \sigma_b^2 \mathbf{A}
\end{bmatrix}
\right)
\quad (\text{PBLUP})
\quad \text{또는} \quad
\mathbf{A} \;\to\; \mathbf{G}\; (\text{GBLUP})
\]
여기서, $\mathbf{b}W$는 환경 변화에 대한 개체별 반응 기울기
$\sigma_{ub}$는 기저수준과 민감도의 공분산: 기저 생산수준이 높은 개체가 스트레스에 더/덜 민감한가?
같은 개체라도 환경에 따라 증감 폭이 다름을 포착하며 이는 $\mathbf{G}\times \mathbf{E}$로 모델링합니다.
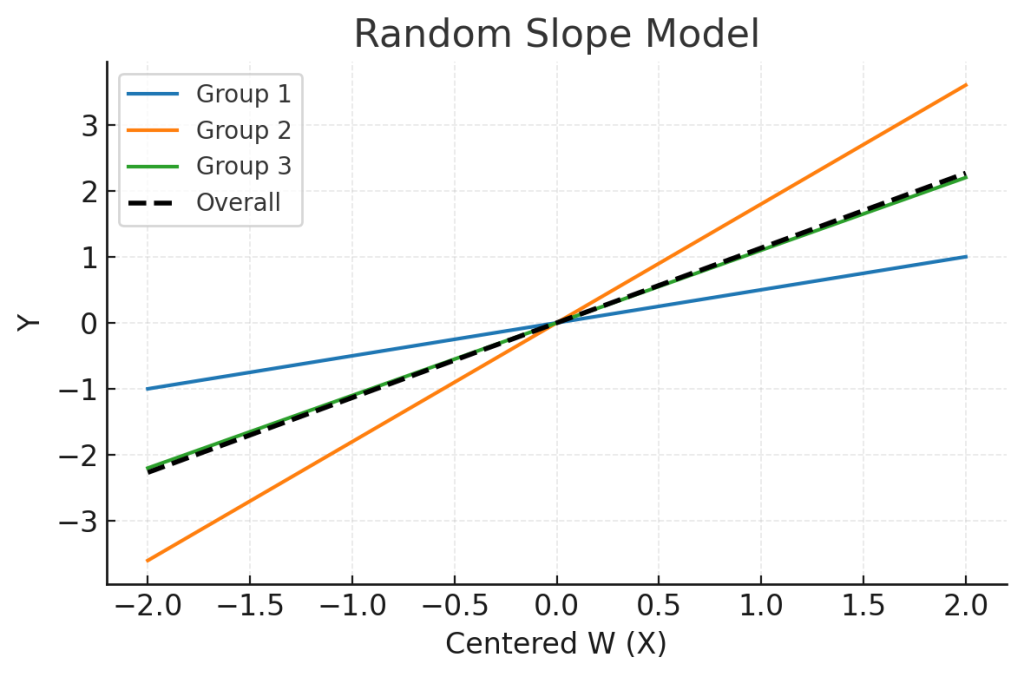
Fig. 2. 랜덤기울기모델 (Random Slope Model)
랜덤절편-기울기모델 (Random intercept-slope model)은 집단별 시작점(절편)도 다르고, 증가/감소 속도(기울기)도 다름을 모델링한 모델입니다.
공변량 $W_{ij}$대한 집단별 기울기를 허용하며 실무에서는 $W$를 센터링($\widetilde{W} = W – \overline{W}$)하여 식별성과 해석력을 높입니다. 즉, 센터 기준점에서 절편과 기울기를 분리합니다.
\[
Y_{ij} = \beta_0 + u_{0j} + \beta_1 X_{ij} + (\beta_W + u_{1j}) \widetilde{W}_{ij} + \varepsilon_{ij}
\]
\[
\begin{bmatrix}
u_{0j} \\
u_{1j}
\end{bmatrix}
\sim \mathcal{N}\!\left(
\begin{bmatrix}
0 \\
0
\end{bmatrix},\;
\begin{bmatrix}
\sigma_{u0}^2 & \sigma_{u01} \\
\sigma_{u01} & \sigma_{u1}^2
\end{bmatrix}
\right)
\]
여기서, $Y_{ij}$는 $j$번째 집단에 속한 $i$번째 개체의 관측값(반응값): 예 학교의 학생의 시험점수, 목장의 소의 체중
$\beta_0$는 전체평균(절편, intercepti): 모든 집단에 적용되는 기저수준
$\beta_1$는 설명변수 $X_{ij}$에 대한 공통기울기
$\beta_W$는 설명변수 $W_{ij}$에 대한 공통기울기(평균적 효과)
$X_{ij}$는 $j$번째 집단의 $i$번째 개체의 설명변수값: 예, 학생의 공부시간, 소의 연령
$W_{ij}$는 집단마다 다른 랜덤 기울기를 허용하는 공변량(설명변수값): 예, 학생의 민감도, 소의 민감도
$u_{0j}$는 $j$번째 집단의 랜덤 절편 (randdom slope): 예 학교별 차이, 목장별 차이
$u_{1j}$는 $j$번째 집단의 랜덤 기울기 (randdom slope): 예 학교별 민감도, 목장별 민감도
$\sigma_{u0}^2$는 절편의 분산 (집단 간 평균 차이의 크기)
$\sigma_{u1}^2$는 기울기의 분산 (집단 간 민감도 차이의 크기)
$\sigma_{u01}^2$는 절편과 기울기 사이의 공분산: 예 평균이 높은 집단이 변화에도 민감한지/덜 민감한지
$\epsilon_{ij}$는 개체수준의 잔차: 예 집단내에서 개체별 변동
유전평가에서의 예로는 랜덤회귀모델(Random Regression Model, RRM)이 있습니다. 낙농 test-day 산유량의 일수(또는 DIM)에 대한 레전드르 다항식 $\phi_k(\mathrm{DIM}_{it})$에 대한 랜덤 회귀모델은 다음과 같습니다.
\[
Y_{it} = \mathbf{x}_{it}^{\top}\boldsymbol{\beta}
+ \sum_{k=0}^{K} \phi_k(\mathrm{DIM}_{it}) \,(a_{ik} + p_{ik})
+ \varepsilon_{it}
\]
여기서, $\phi_k(\mathrm{DIM}_{it})$는 일수(DIM, Days in Milk)에 따른 기저 함수(예: 레전드르 다항식)
$u_{ik}$는 개체 $i$의 유전적 랜덤 회귀계수
$p_{ik}$는 개체 $i$의 영속환경(permanent environment) 랜덤 회귀계수
$\epsilon_{it}$는 잔차
Table 1. PBLUP·GBLUP의 유전적 관계, 반응규범, 랜덤회귀 비교
| 항목 | PBLUP | GBLUP |
|---|---|---|
| 유전적 관계 | $\mathbf{A}$ (혈통) | $\mathbf{G}$ (유전체) |
혼합선형모델 (랜덤 절편) | $\mathbf{y}=\mathbf{X}\boldsymbol{\beta}+\mathbf{Z}_a\mathbf{a}+\mathbf{e}$ | $\mathbf{y}=\mathbf{X}\boldsymbol{\beta}+\mathbf{Z}_g\mathbf{a}+\mathbf{e}$ $ |
반응규범(G×E) (랜덤 절편+기울기) | $ \begin{bmatrix}\mathbf{a}\\ \mathbf{b}\end{bmatrix} \sim \mathcal{N}\!\Big( \mathbf{0},\; \begin{bmatrix} \sigma_a^2\mathbf{A} & \sigma_{ab}\mathbf{A}\\ \sigma_{ab}\mathbf{A} & \sigma_b^2\mathbf{A} \end{bmatrix} \Big) $ | $ \begin{bmatrix}\mathbf{g}\\ \mathbf{b}\end{bmatrix} \sim \mathcal{N}\!\Big( \mathbf{0},\; \begin{bmatrix} \sigma_a^2\mathbf{G} & \sigma_{ab}\mathbf{G}\\ \sigma_{ab}\mathbf{G} & \sigma_b^2\mathbf{G} \end{bmatrix} \Big) $ |
| 랜덤회귀(RRM) | $\mathbf{A}\otimes\boldsymbol{\Omega}$ | $\mathbf{G}\otimes\boldsymbol{\Omega}$ |
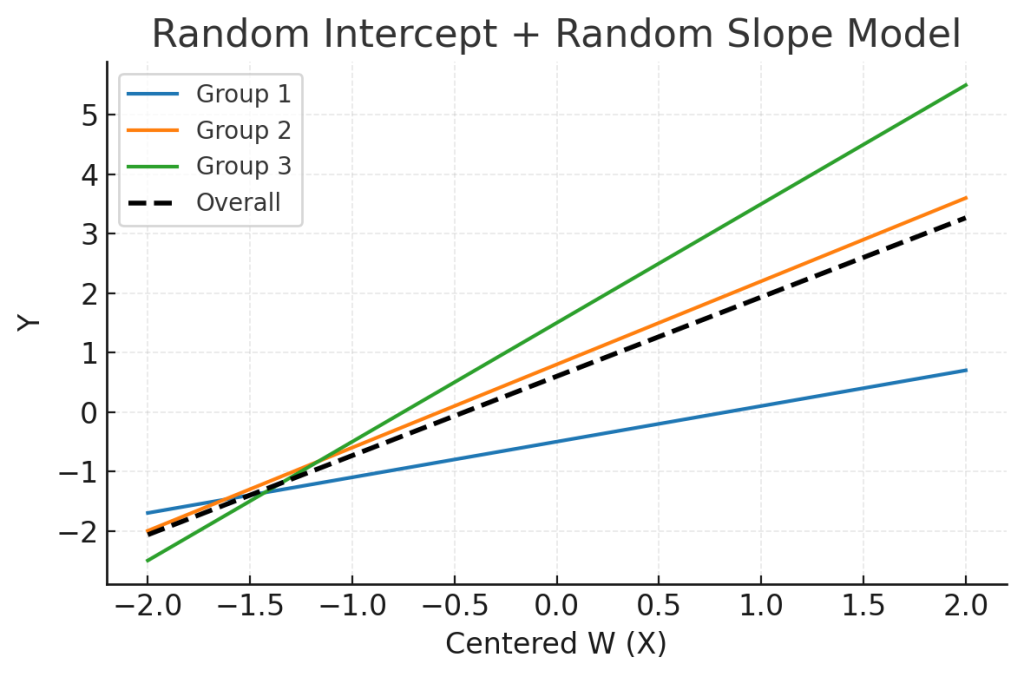
Fig. 3. 랜덤절편-기울기모델 (Random intercept-slope model)