네, 그렇습니다.
수학적 함수 관점에서는 우도함수의 종속변수는 우도이고 독립변수는 모수입니다.
확률분포함수(확률밀도함수 또는 확률질량함수)의 독립변수를 관측된 데이터로 고정하고 매개변수인 모수를 독립변수로 취급하는 함수가 우도함수입니다.
무엇보다 중요한 점은 우도함수는 함수값으로 확률을 나타내는 것이 아니라 우도를 나타낸다는 것입니다.
우도는 확률이 아니라 주어진 데이터에서의 모수의 그럴듯함의 정도라고 할 수 있습니다.
확률변수가 데이터로 실현되면 우도도 우도값으로 수치화할 수 있습니다.
확률분포함수는 확률변수가 연속형일 때는 확률밀도함수(probability density function, pdf)입니다. 즉, pdf는 연속형 확률변수의 분포를 나타내는 함수입니다.
$$f(y \mid \theta)$$
확률변수가 이산형일때는 확률질량함수(probability mass function, pmf)입니다. 즉, pmf는 이산형 확률변수의 분포를 나타내는 함수입니다.
$$P(y \mid \theta)$$
확률밀도함수와 확률질량함수를 통틀어서 확률분포함수(probability distribution function)라고 부릅니다.
확률밀도함수(probability density function, pdf)는 모수를 조건으로 하는 데이터의 함수인 데 이를 데이터를 고정으로하는 모수의 함수로 바꾸면 우도함ㅎ수가 됩니다.
$$L(\theta; y) = f(y \mid \theta)$$
마찬가지로 확률질량함수(probability mass function, pmf)는 모수를 조건으로 하는 데이터의 함수인 데 이를 데이터를 고정으로하는 모수의 함수로 바꾸면 우도함수가 됩니다.
$$L(\theta; y) = P(y \mid \theta)$$
확률분포의 형태를 결정하는 매개변수와 독립변수로 확률변수가 있는 확률분포함수에서 확률변수의 관측값으로 독립변수를 고정하고 매개변수인 모수의 함수로 재해석한 함수가 우도함수입니다.
1. 정규분포의 확률밀도함수 (PDF)
정규분포 \( \mathcal{N}(\mu, \sigma^2) \) 의 확률밀도함수는 다음과 같습니다.
$$
f(x \mid \mu, \sigma^2)
= \frac{1}{\sqrt{2\pi\sigma^2}}
\exp\left( -\frac{(x – \mu)^2}{2\sigma^2} \right)
$$
2. 표본이 여러 개인 경우
표본이 \( n \)개, 즉 \( x_1, x_2, \ldots, x_n \)이 독립이고 동일분포(i.i.d.)라고 하면,
공동확률밀도함수(joint pdf)는 곱으로 표현됩니다.
$$
f(x_1, \ldots, x_n \mid \mu, \sigma^2)
= \prod_{i=1}^n f(x_i \mid \mu, \sigma^2)
$$
3. 우도함수 (Likelihood function)
주어진 데이터 \( \mathbf{x} = (x_1, \ldots, x_n) \)에 대해
모수 \( \mu, \sigma^2 \)를 변수로 보는 함수가 바로 우도함수입니다.
$$
L(\mu, \sigma^2; \mathbf{x})
= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}
\exp\left( -\frac{(x_i – \mu)^2}{2\sigma^2} \right)
$$
4. 로그우도함수 (Log-likelihood function)
곱을 취급하기 편하게 로그를 취하면 다음과 같습니다.
$$
\ell(\mu, \sigma^2; \mathbf{x}) = \log L(\mu, \sigma^2; \mathbf{x})
$$
$$
= -\frac{n}{2} \log (2 \pi \sigma^2)
– \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i – \mu)^2
$$
5. 해석
– 우도함수 \( L(\mu, \sigma^2; \mathbf{x}) \) 는 데이터가 주어졌을 때, “이 데이터가 해당 모수값에서 얼마나 그럴듯하게 나왔는가”를 나타냅니다.
– 최대우도추정량(MLE)은 이 우도함수를 최대화하는 \(\mu, \sigma^2\)입니다.
$$
\hat{\mu} = \bar{x}, \quad
\hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (x_i – \bar{x})^2
$$
데이터(data)는 다음과 같습니다.
$$
y = [5.2, \; 4.8, \; 5.0, \; 5.4, \; 5.1]
$$
– 평균 (sample mean)
$$\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i
= \frac{5.2 + 4.8 + 5.0 + 5.4 + 5.1}{5}
= \frac{25.5}{5} = 5.10$$
– 분산 (MLE 기준, 표본크기=n)
$$\hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^{n} (y_i – \bar{y})^2= \frac{0.20}{5} = 0.04$$
– 가로축: 모수 $\mu$ (평균)
– 세로축: Likelihood $L(\mu; \text{data})$
– 파란색 곡선: 모수 값에 따른 우도함수
– 빨간 점선: 최대우도추정치 (MLE) $\hat{\mu} \approx 5.10$
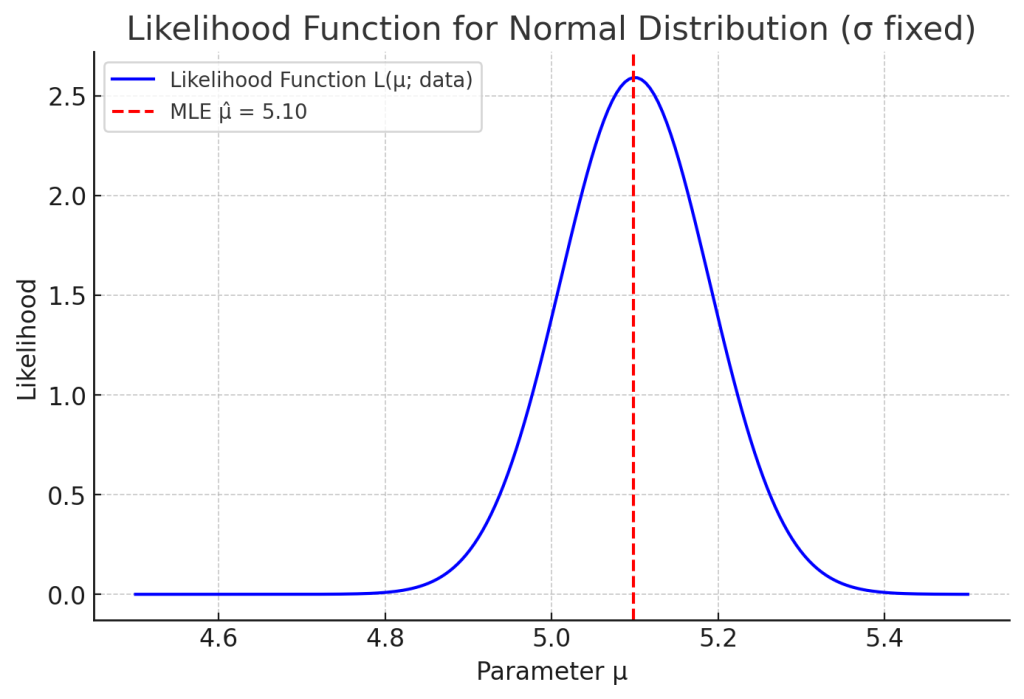
Fig. 1. 평균에 대한 우도함수 곡선 (분산고정)
– 가로축: 모수 $\sigma^2$ (분산)
– 세로축: Likelihood $L(\sigma^2; \text{data})$
– 녹색 곡선: 분산 값에 따른 우도
– 빨간 점선: 최대우도추정치 (MLE) $\hat{\sigma}^2 \approx 0.040$
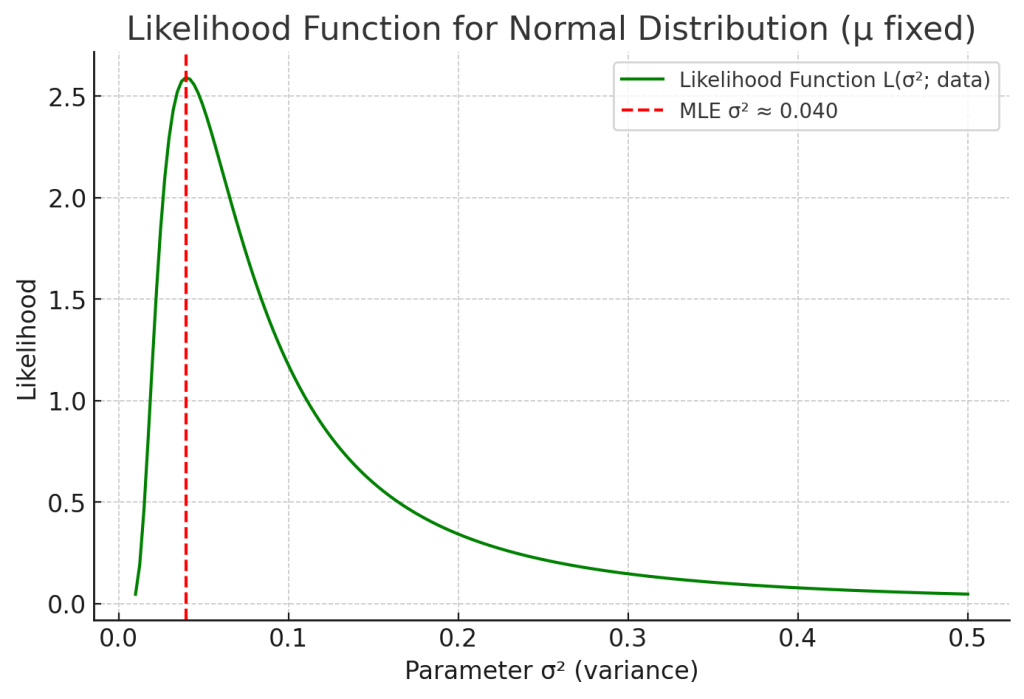
Fig. 2. 분산에 대한 우도함수 곡선 (평균고정)
– x축: 평균 $\mu$
– y축: 분산 $\sigma^2$
– 등고선: 같은 우도 값을 갖는 곡선
– 빨간 x 표시: 최대우도추정치 (MLE) $\hat{\mu} \approx 5.08, \; \hat{\sigma}^2 \approx 0.041$
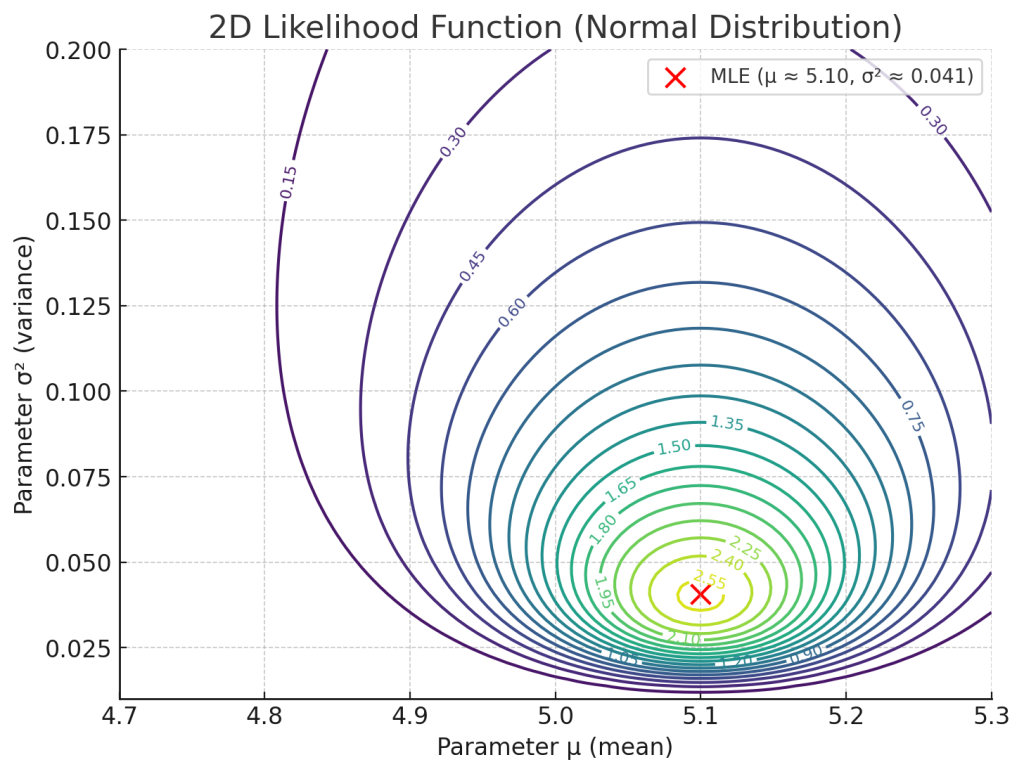
Fig. 3. 정규분포의 평균과 분산을 동시에 추정하는 2차원 우도함수
– x축: 평균 $\mu$
– y축: 분산 $\sigma^2$
– z축: 우도값 $L(\mu, \sigma^2; \text{data})$
– 곡면: 주어진 데이터에 대해 $(\mu, \sigma^2)$가 달라질 때의 우도함수 값
– 빨간 점: 최대우도추정치 (MLE) $\hat{\mu} \approx 5.10, \; \hat{\sigma}^2 \approx 0.039$
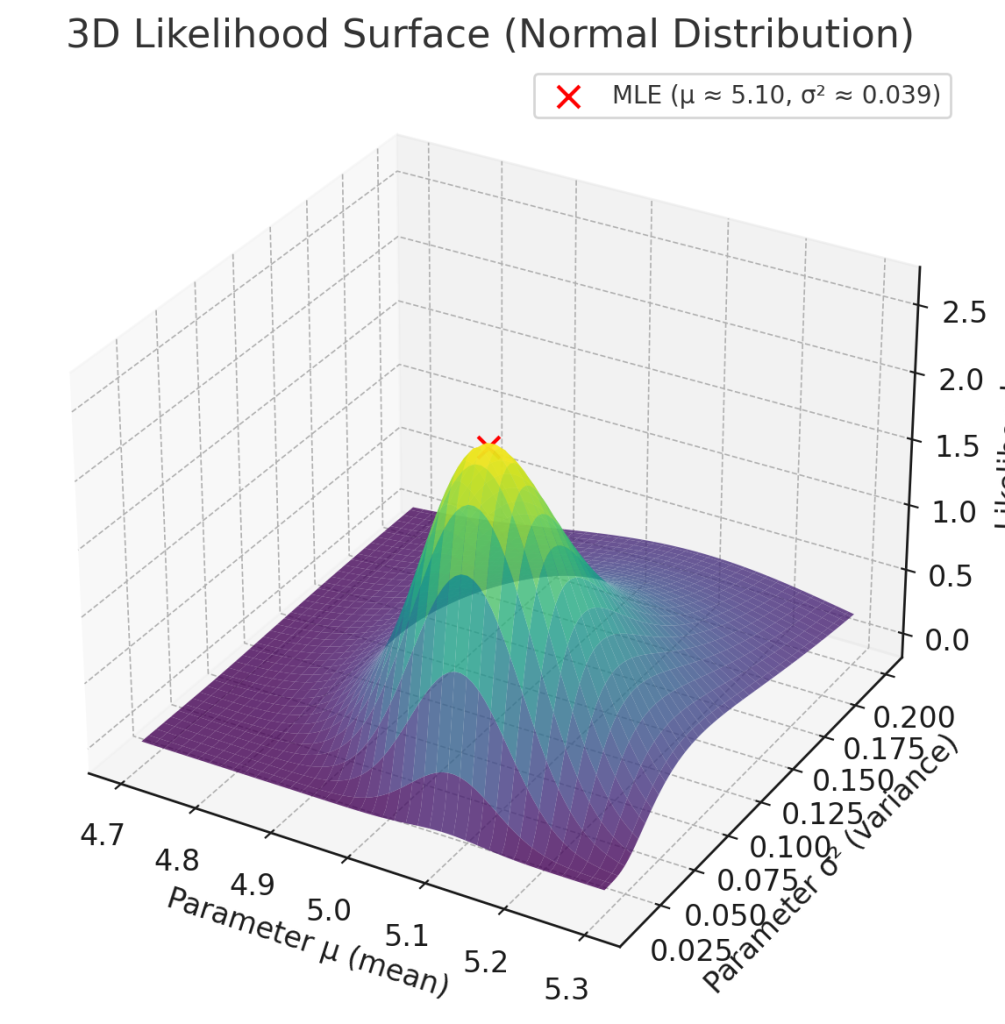
Fig. 4. 정규분포의 평균과 분산을 동시에 추정하는 3차원 우도함수
– x축: 평균 $\mu$
– y축: 분산 $\sigma^2$
– 등고선: 로그우도의 값
– 빨간 x: MLE $\hat{\mu} \approx 5.10, \; \hat{\sigma}^2 \approx 0.039$
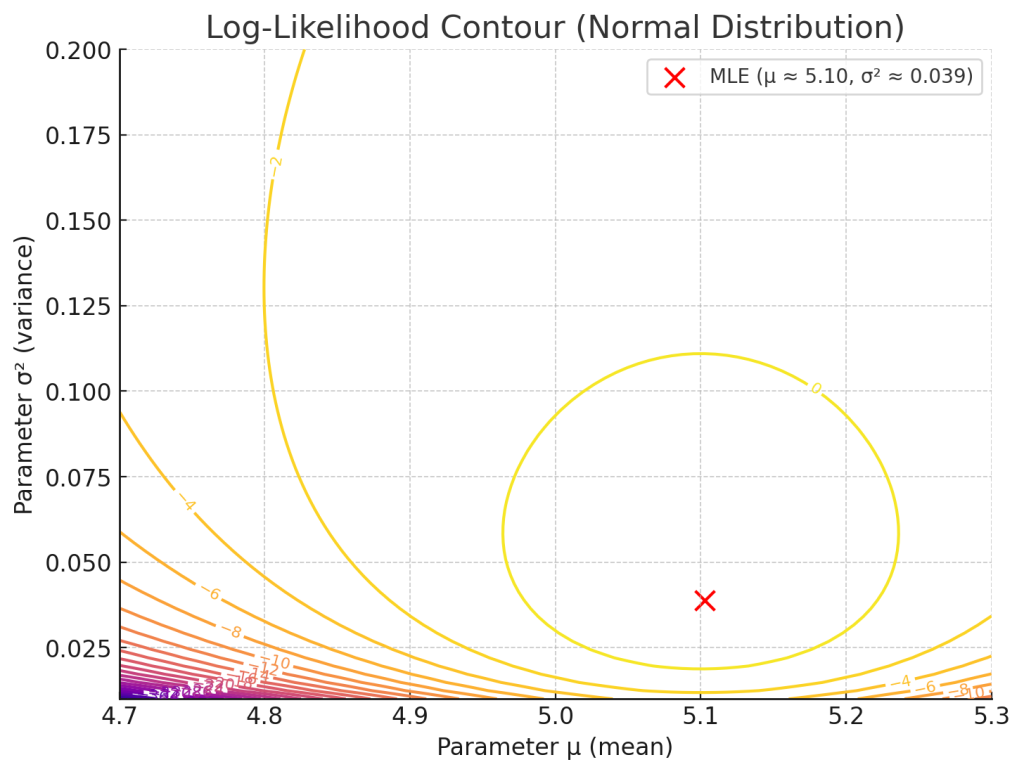
Fig. 5. 정규분포의 평균과 분산을 동시에 추정하는 2차원 로그우도함수
– x축: 평균 $\mu$
– y축: 분산 $\sigma^2$
– z축: 로그우도 $\ell(\mu, \sigma^2; \text{data})$
– 곡면: 로그우도의 값
– 빨간 점: 최대우도추정치 (MLE) $\hat{\mu} \approx 5.10, \; \hat{\sigma}^2 \approx 0.039$
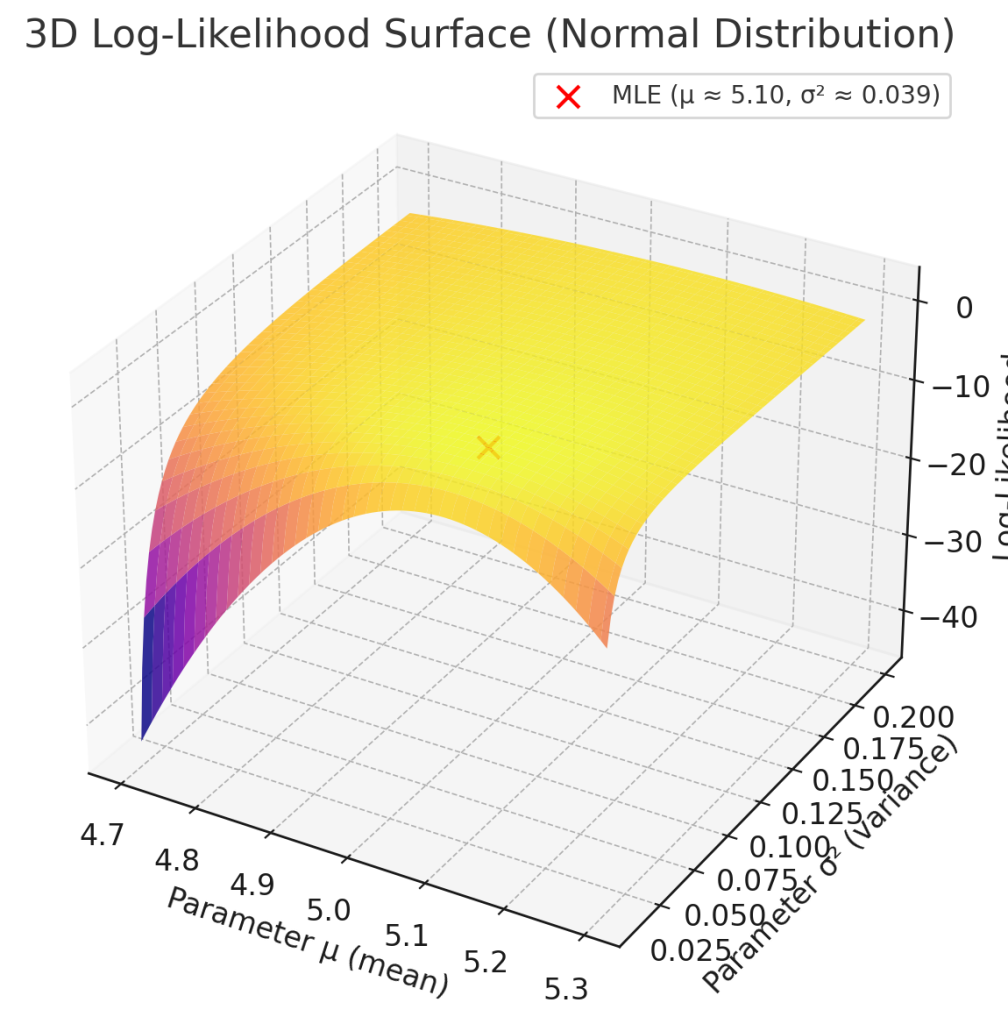
Fig. 6. 정규분포의 평균과 분산을 동시에 추정하는 3차원 로그우도함수