히스토그램과 확률밀도함수 ?
2.1. 히스토그램과 확률밀도함수
1. 애니메이션
2. 설명
2.1 히스토그램과 확률밀도함수
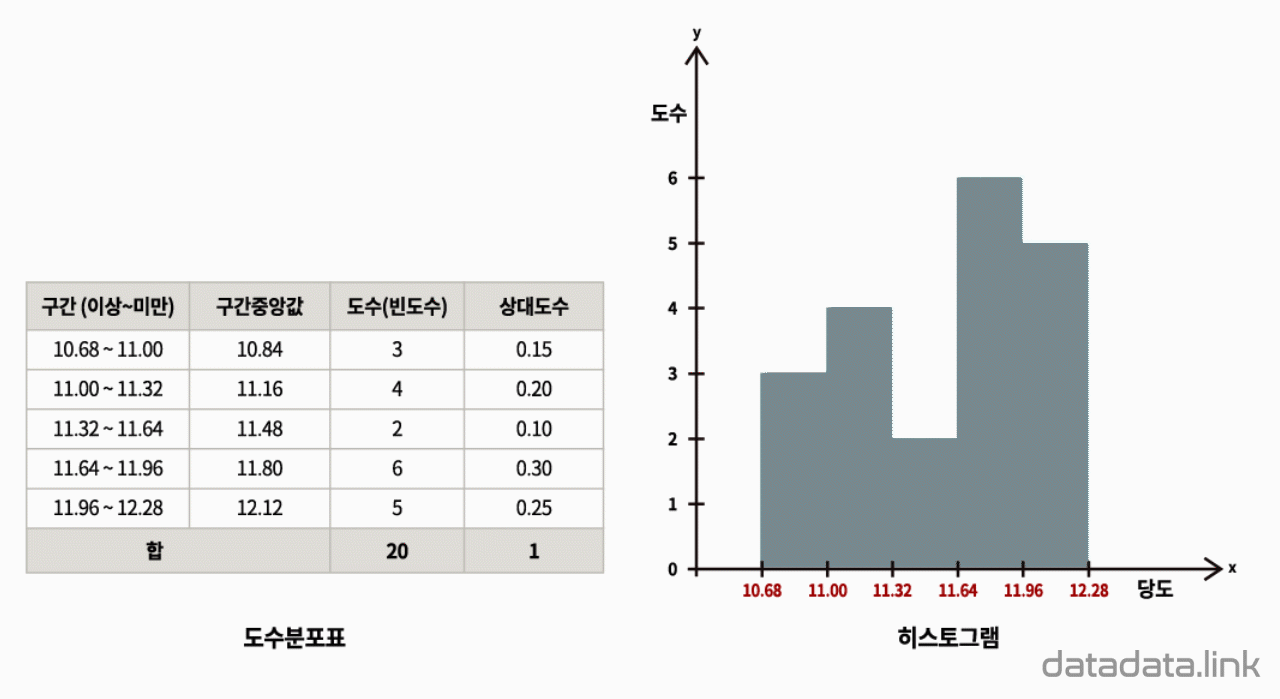
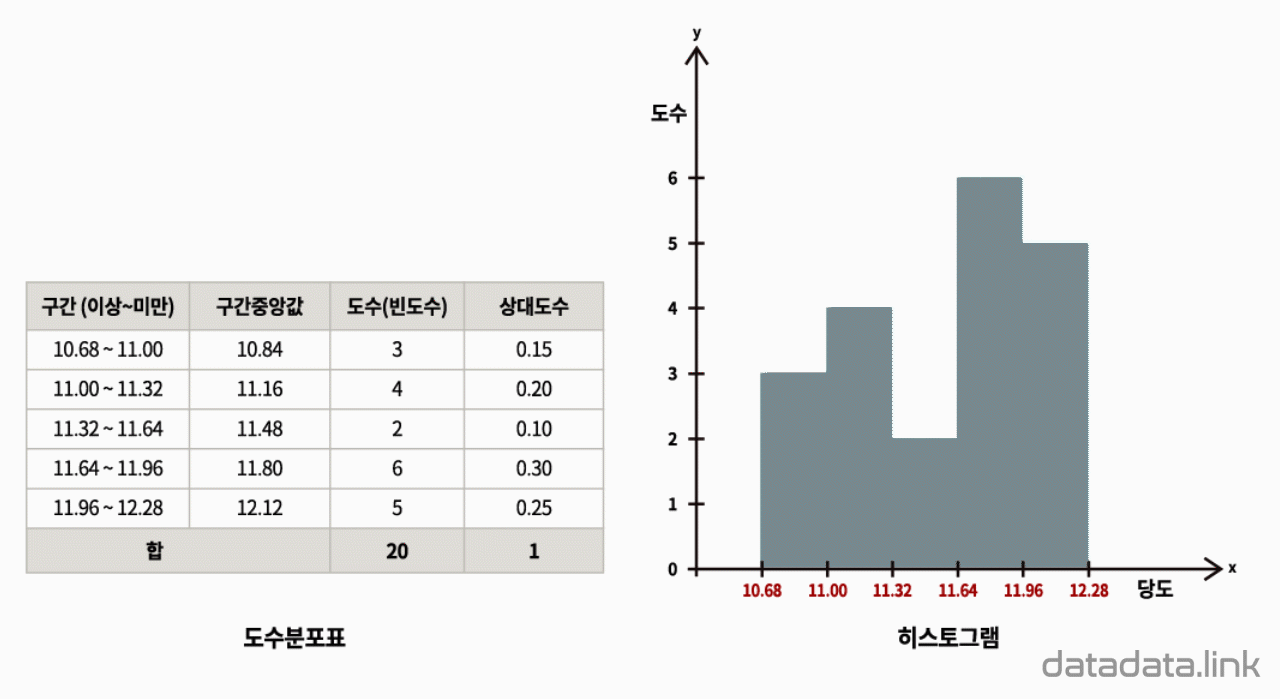
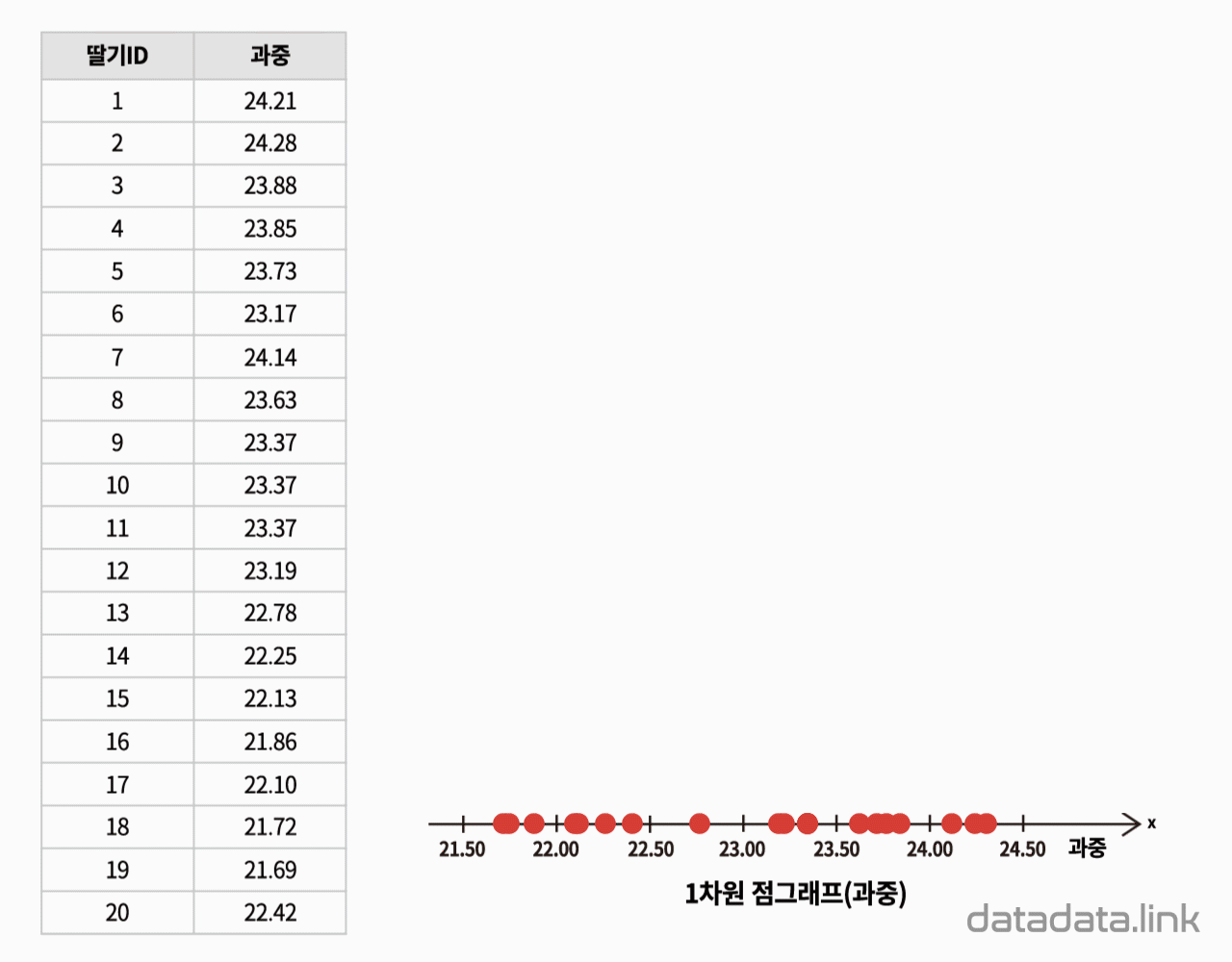
도수분포를 관찰하기 위하여 도수분포표를 만듭니다. 같은 간격으로 변수의 구간을 정하였을 때, 각 구간에 속하는 변수값(데이터)의 갯수를 도수(빈도수)라고 합니다. 도수는 각 구간에 변수가 나타나는 횟수입니다. 구간별로 도수를 나타내는 표가 도수분포표입니다.
도수분포표를 시각화하는 것이 히스토그램입니다. 히스토그램은 각 구간을 직사각형으로 표현하는데 밑변은 구간의 간격이 되고 높이는 빈도수를 나타냅니다. 여기서 빈도수를 상대 빈도수로 바꾸면 히스토그램을 이루는 직사각형의 높이는 그 구간을 대표하는 확률인 확률질량을 나타냅니다. 각 구간의 확률질량을 모두 더하면 1이 됩니다. 각 구간의 상대도수는 각 구간의 빈도수를 전체 빈도수로 나눈 값입니다. 즉, 전체 빈도수에서 각 구간의 빈도수가 차지하는 비율입니다.
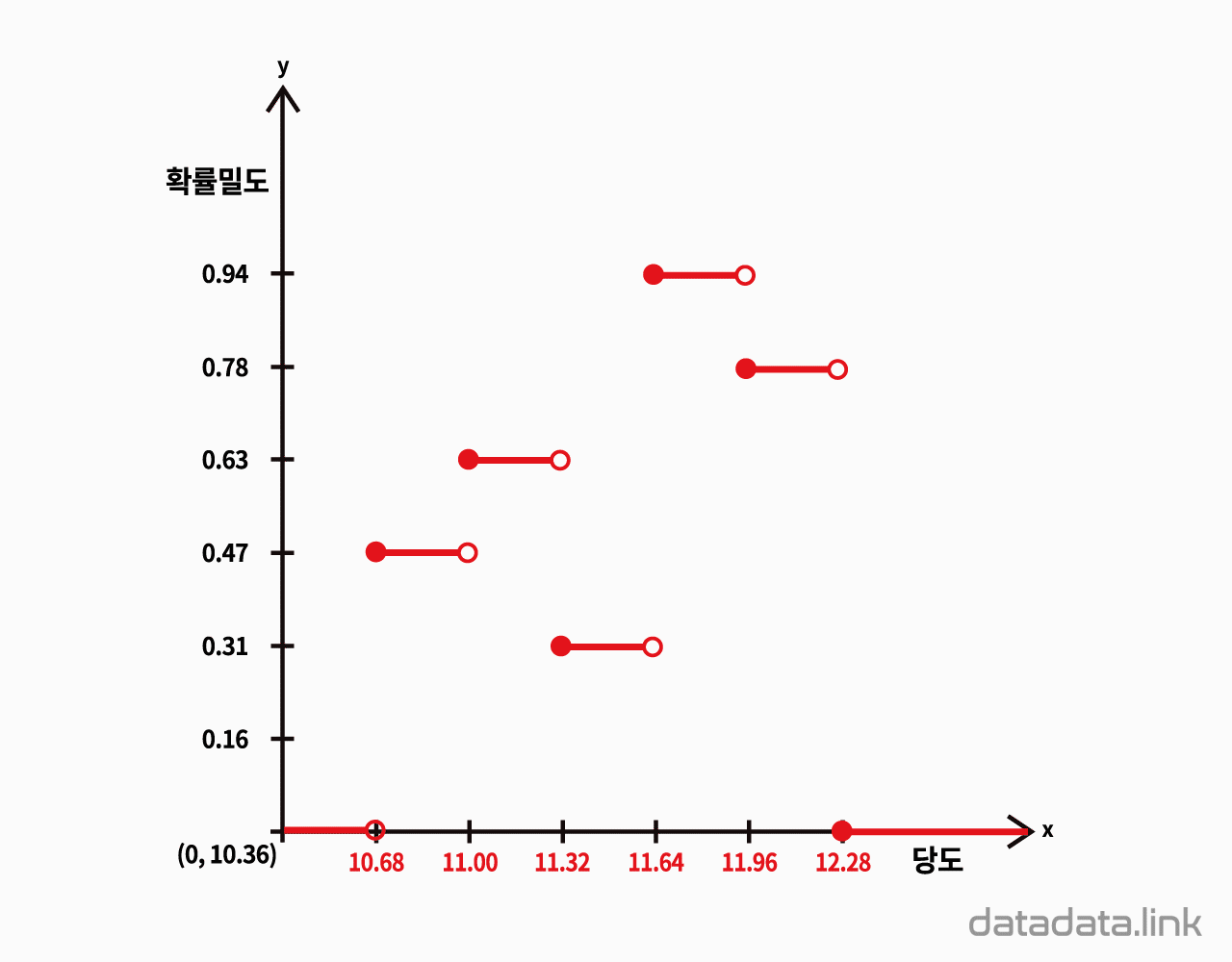
히스토그램이 나타내는 도수를 상대도수로 바꾼 것을 상대도수 히스토그램이라 하겠습니다. 상대도수 히스토그램을 다시 확률밀도 함수로 바꾸어 봅니다. 상대도수 히스토그램에서 구간의 간격으로 상대도수를 나누면 상대도수 히스토그램은 확률밀도함수를 나타냅니다. 즉, 상대도수를 구간의 간격으로 나눈 값이 확률밀도가 됩니다. 각 구간의 직사각형의 윗변의 처음과 시작을 이상과 미만으로 표시하면 확률밀도함수를 나타냅니다. 이 확률밀도함수는 모양은 이산(discrete)로 나타남으로 이산확률밀도함수입니다.
만일, 상대도수 히스토그램의 간격이 무한소가 되면서 동시에 상대도수를 구간의 간격으로 나눈다면 상대도수 히스토그램은 연속확률밀도함수로 변화합니다.
3. 실습
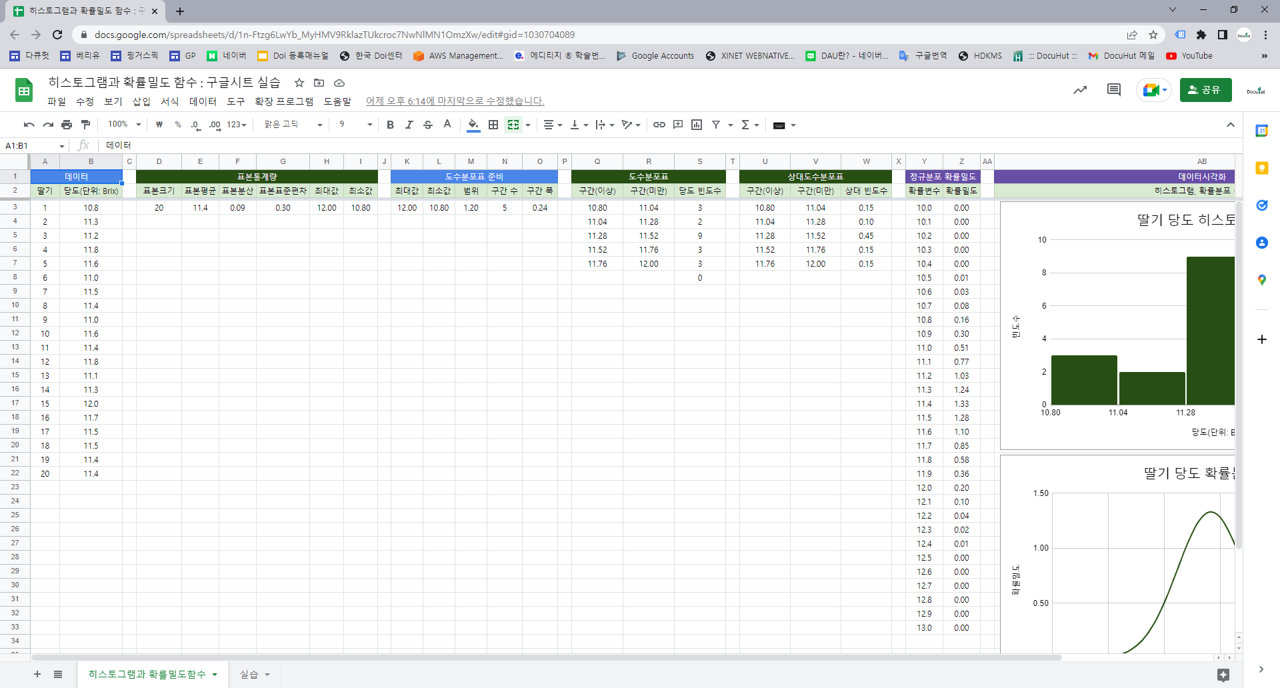
3.2. 구글시트 함수
=COUNT(B3:B22) : 데이터 개수. B3에서 B22에 있는 숫자로 표시된 데이터의 개수.
=AVERAGE(B3:B22) : 평균. B3에서 B22에 있는 데이터의 평균.
=VAR.S(B3:B22) : 표본분산. B3에서 B22에 있는 데이터의 표본분산. 편차제곱합을 데이터 개수 -1로 나눔.
=STDEV.S(B3:B22) : 표본표준편차. B3에서 B22에 있는 데이터의 표본표준편차. 표본분산의 제곱근.
=MIN(B3:B22) : 최소값. B3에서 B22에 있는 데이터 중에서 최소값을 표시함.
=MAX(B3:B22) : 최대값. B3에서 B22에 있는 데이터 중에서 최대값을 표시함.
=SQRT(D3) : 제곱근. D3값의 제곱근.
=ROUNDUP(SQRT(D3)) : 올림. D3값의 제곱근의 올림값.
=ROUND(M3/N3,2) : 반올림. M3값을 N3값으로 나눈 값을 반올림해서 소수점 2번째자리까지 표시.
=FREQUENCY(B3:B22,R3:R7) : 빈도수. B3에서 B22에 있는 데이터를 R3에서 R7까지의 구간에 맞춰 빈도수를 구함.
=S3/SUM(S3:S7) : 합계. S3에서 S7에 있는 데이터의 합계.
=NORMDIST(Y3,E3,G3,FALSE) : 정규분포 확률밀도. E3가 평균, G3가 표준편차인 정규분포 상에서 Y3값의 확률밀도를 계산함. FALSE 대신 TRUE를 넣으면, 누적확률밀도를 계산함.
3.3. 실습강의
– 데이터
– 표본통계량
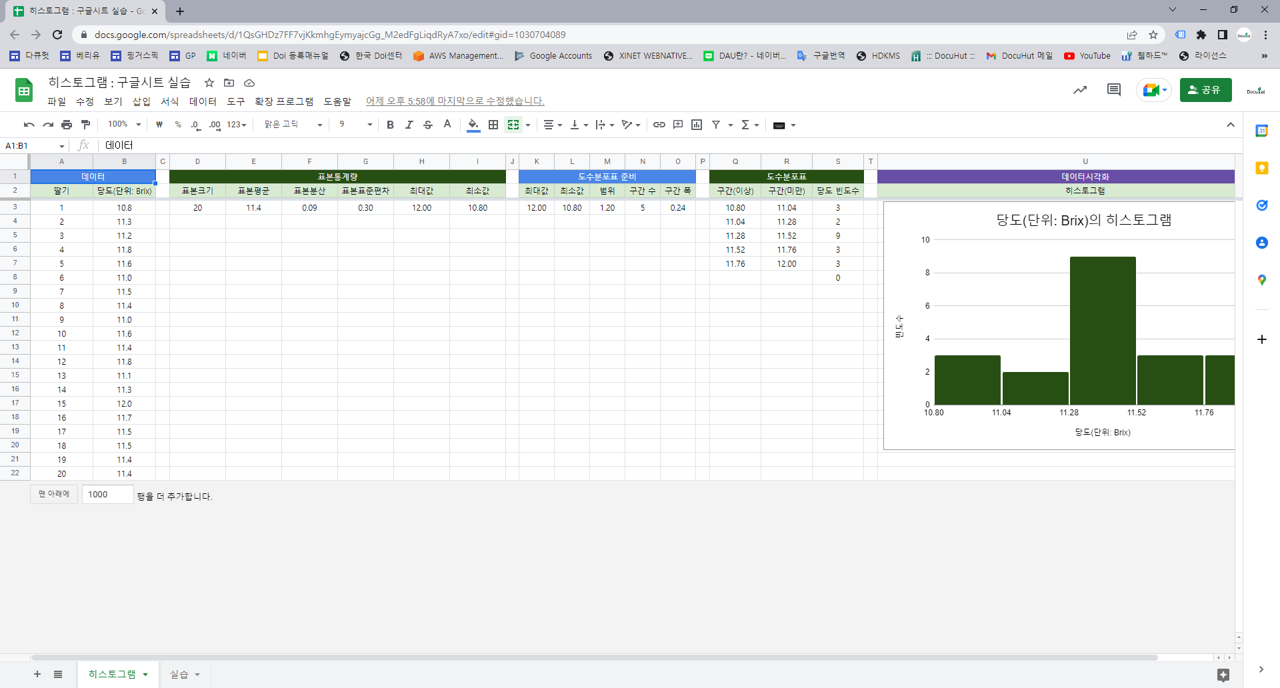
– 도수분포표
– 히스토그램
– 상대도수 히스토그램
– 정규분포
– 실습 안내
4. 용어와 수식
4.1 용어
히스토그램
데이터값의 분포를 표현하는 방식중의 하나입니다. 연속확률변수의 확률값을 막대그래프 모양으로 표현한 것입니다. Karl Pearson에 의해 처음 소개되었습니다.
히스토그램을 작성하려면 먼저 변수 범위를 구간(“bin”또는 “bucket”)으로 나눕니다. 그리고 각 구간에 몇 개의 데이터 값이 속하는 지를 정리합니다. 구간은 연속적이고 겹치지 않고 인접해야 하며 같은 간격이면 분석에 용이합니다.(구간 간격이 꼭 같아야 하는 것은 아닙니다.)
직사각형(막대)의 높이에 비례하는 빈도수는 상대빈도수로 정규화될 수 있습니다. 구간들이 동일한 간격이고 간격이 1인 경우, 빈도수를 정규화하게 되면 각 직사각형의 높이는 상대빈도수를 표현하는 확률이 되어 각 직사각형의 높이의 합은 1이 됩니다. 그러나 구간은 동일한 폭(구간크기)일 필요는 없습니다. 이 경우 직사각형(막대)은 구간의 빈도수에 비례하는 면적을 갖도록 정의됩니다 . 수직축은 빈도수가 아니라 빈도수밀도(수평축상의 변수의 단위당 경우의 수)입니다. 모양은 막대 그래프의 막대가 서로 인접한 모양으로 변수가 연속적으로 표현되었다는 것이 중요합니다.
히스토그램은 데이터의 기본 확률분포밀도를 대략적으로 나타내며, 확률밀도 추정시 자주 사용됩니다 . 즉, 기본 확률변수의 확률밀도함수를 나타냅니다 . 확률 밀도에 사용되는 히스토그램의 총 면적은 항상 1로 정규화됩니다. $X$ 축의 간격이 모두 1이면 히스토그램은 상대빈도 막대그래프와 동일합니다 . 히스토그램은 통계적 속성을 모델링해야 할 때 통계 패키지 프로그램에서 자주 쓰입니다. 예를 들면, 커널 밀도 추정치의 상관 관계 변이는 수학적으로 설명하기가 매우 어렵지만 각 구간이 독립적으로 변하는 히스토그램에서는 이해하기가 쉽습니다. 커널 밀도 추정의 대안은 평균 이동된 히스토그램입니다 계산 속도는 빠르며 커널을 사용하지 않고 밀도를 부드럽게 계산할 수 있습니다.
히스토그램은 때때로 막대그래프와 혼동됩니다.히스토그램은 연속 데이터에 사용되기 때문에 막대는 붙어 있게 됩니다. 그래서 구별을 분명히 하기 위해 막대그래프는 막대 사이에 간격을 줍니다.
Reference
확률밀도함수
확률에서 확률밀도함수(PDF) 또는 연속확률변수의 밀도는 표본공간의 임의의 표본(또는 점)의 확률변수의 값이 같다면 같은 확률을 가진다는 것입니다. 다른 말로 하면, 임의의 연속확률변수에 대한 확률값은 0이지만 두 개의 서로 다른 확률변수 값에서 PDF의 값을 사용하여 유추할 수는 있습니다. PDF는 임의의 확률변수에서의 확률값을 취하는 것보다는 특정 확률변수 범위 내에서 임의의 확률변수가 있을 확률을 나타내는데 사용됩니다. 확률은 확률변수의 범위에 대한 PDF의 적분값으로 주어집니다. 확률밀도함수는 모든 곳에서 음수가 아니며 전체 확률변수범위에 대한 적분은 1이 됩니다.
“확률분포함수”와 “확률함수”라는 용어는 때로는 확률밀도함수를 의미하기도 하지만 이 용어는 표준이 아닙니다. 한편, 확률질량함수(PMF)는 이산확률변수 (불연속 확률변수)에서 사용되는 반면, 확률밀도함수(PDF)는 연속확률변수에서 사용됩니다.
Reference
Probability density function – Wikipedia