정규분포 ?
Normal distribution ?
1.1. 정규분포
4.1. 참조
1. 애니메이션
2. 설명
2.1. 이항분포
확률변수인 성공횟수($K$)가 시행횟수($N$)와 성공확률($P$)을 매개변수(parameter, 모수)로 가지는 이항분포를 따르면
$$K\sim B\left({n,p}\right)$$
$n$번 시행중에 $k$번 성공할 확률은 다음과 같이 확률질량함수로 주어집니다.
$$Pr\left({{K}{=}{k}}\right){=}{f}\left({k\,;n,p}\right){=}\left({\frac{n}{k}}\right){p}^{k}{\left({{1}{-}{p}}\right)}^{{n}{-}{k}}$$
확률변수 $X$가 이항분포를 따른다고 하면 다음과 같이 표현합니다.
$$X \sim B\left({n,p}\right)$$
$X$의 기대값은 다음과 같습니다.
$$\mathrm{E}\left[{X}\right]=np$$
분산은 다음과 같습니다.
$$\mathrm{Var}\left(X\right)=np\left({1-p}\right)$$
기대값은
$$\mathrm{E}\left[{X}\right]=\sum\limits_{i=1}^{n}{x_{i}\cdot p_{i}}$$
분산은
$${\rm Var}\left({X}\right)=\sum\limits_{i=1}^{n}{{\left({x_{i}-\mathrm{E}[X]}\right)}^{2}}\cdot p_{i}=\sum\limits_{i=1}^{n}{{x_{i}^{2}\cdot p_{i}}}-{\mathrm{E}[X]}^{2}$$
여기서, $\sum\limits_{i=1}^{n}x_i^2 \cdot p_i={\rm E}[X^2]$
분산등식은
분산 = 제곱의 평균 – 평균의 제곱
분산등식을 수식으로 표현하면
$$\rm{Var}\left({X}\right)=\mathrm{E}\left[{X^{2}}\right]-\mathrm{E}{\left[{X}\right]}^{2}$$
2.2. 이항분포 ~ 정규분포
$X\sim B\left({n,p}\right)$ 에서 $n$이 충분히 클 때 $X\sim N\left({np,\sqrt{np\left({1-p}\right)}}\right)$로 근사합니다.
$X\sim N\left({\mu ,\sigma^{2}}\right)$
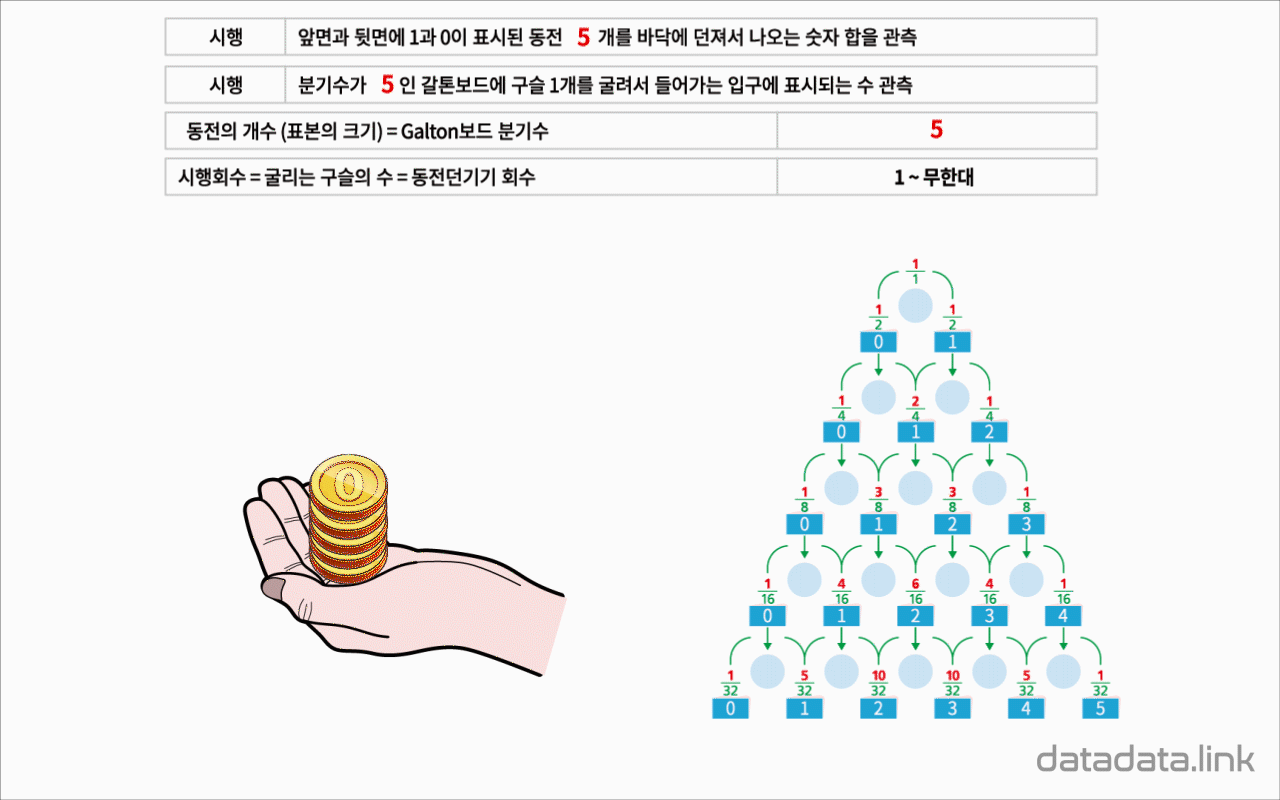
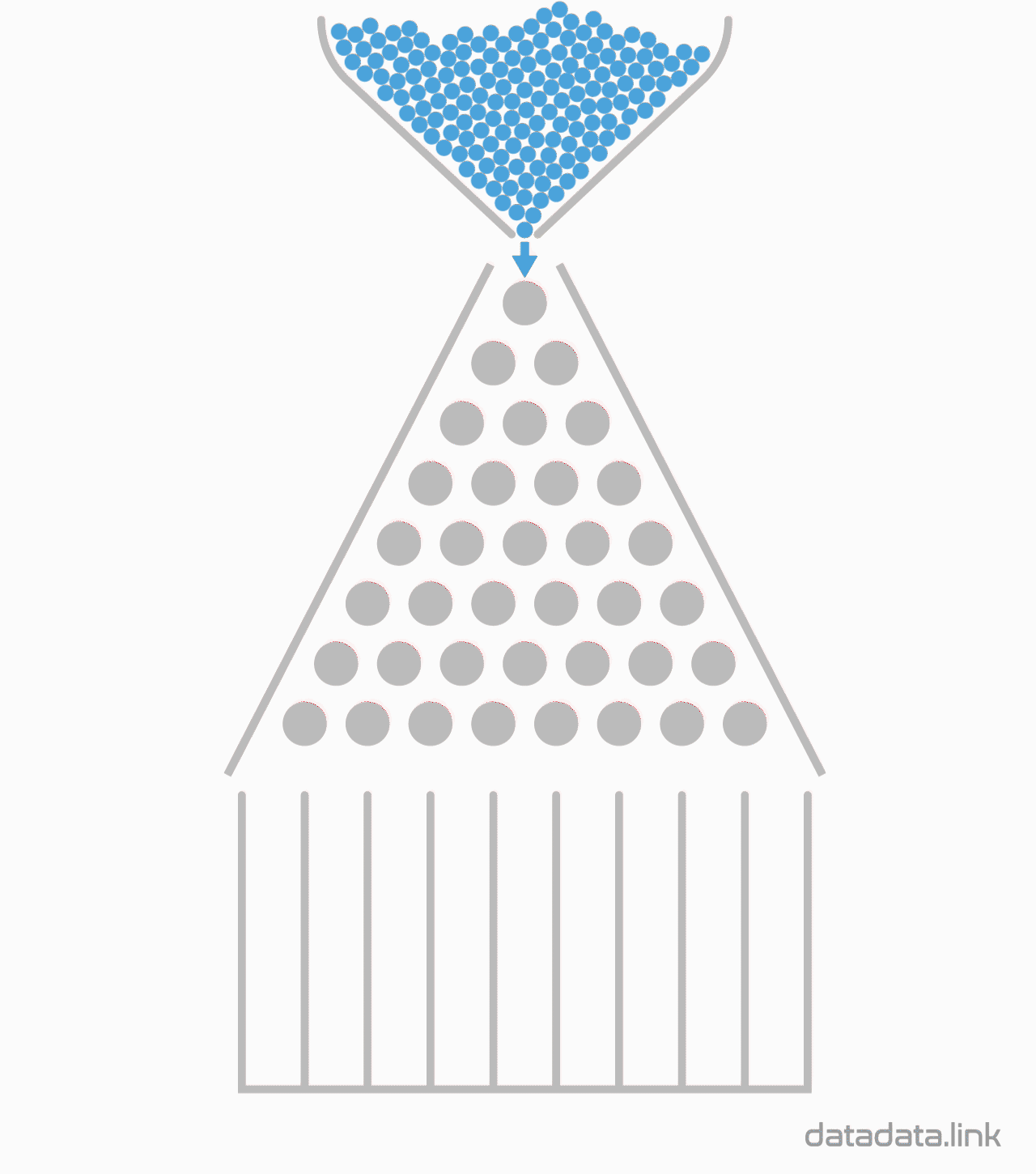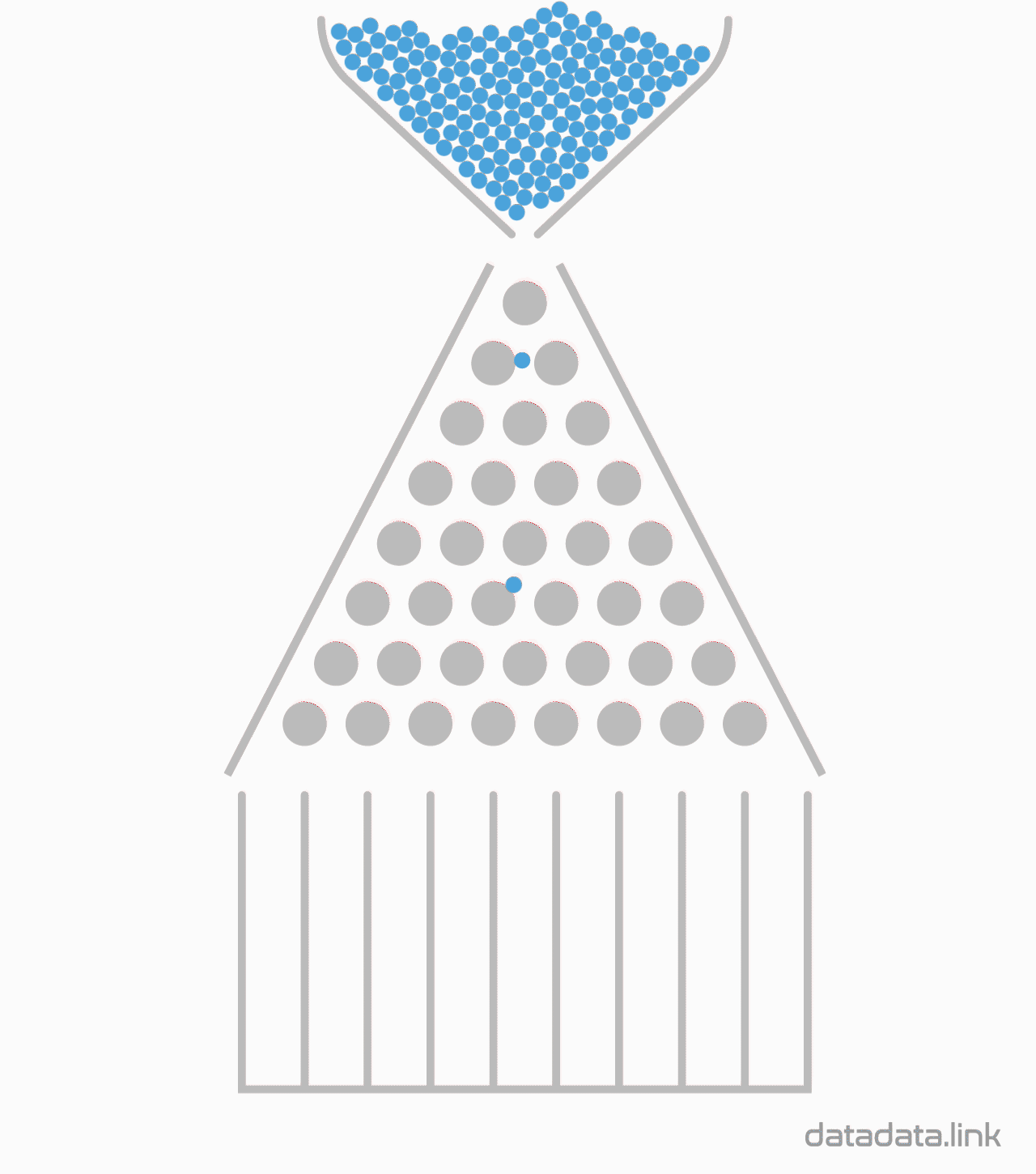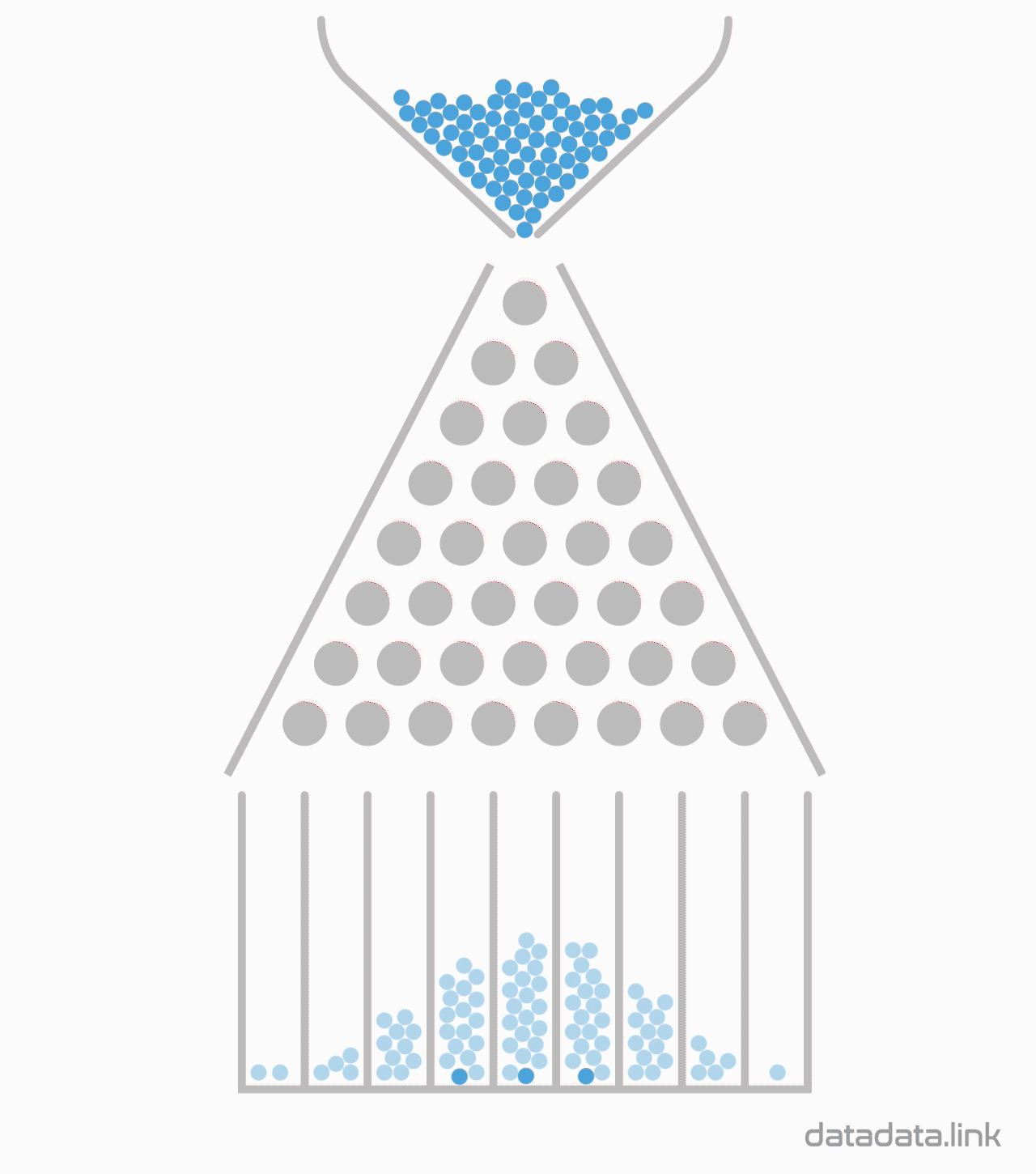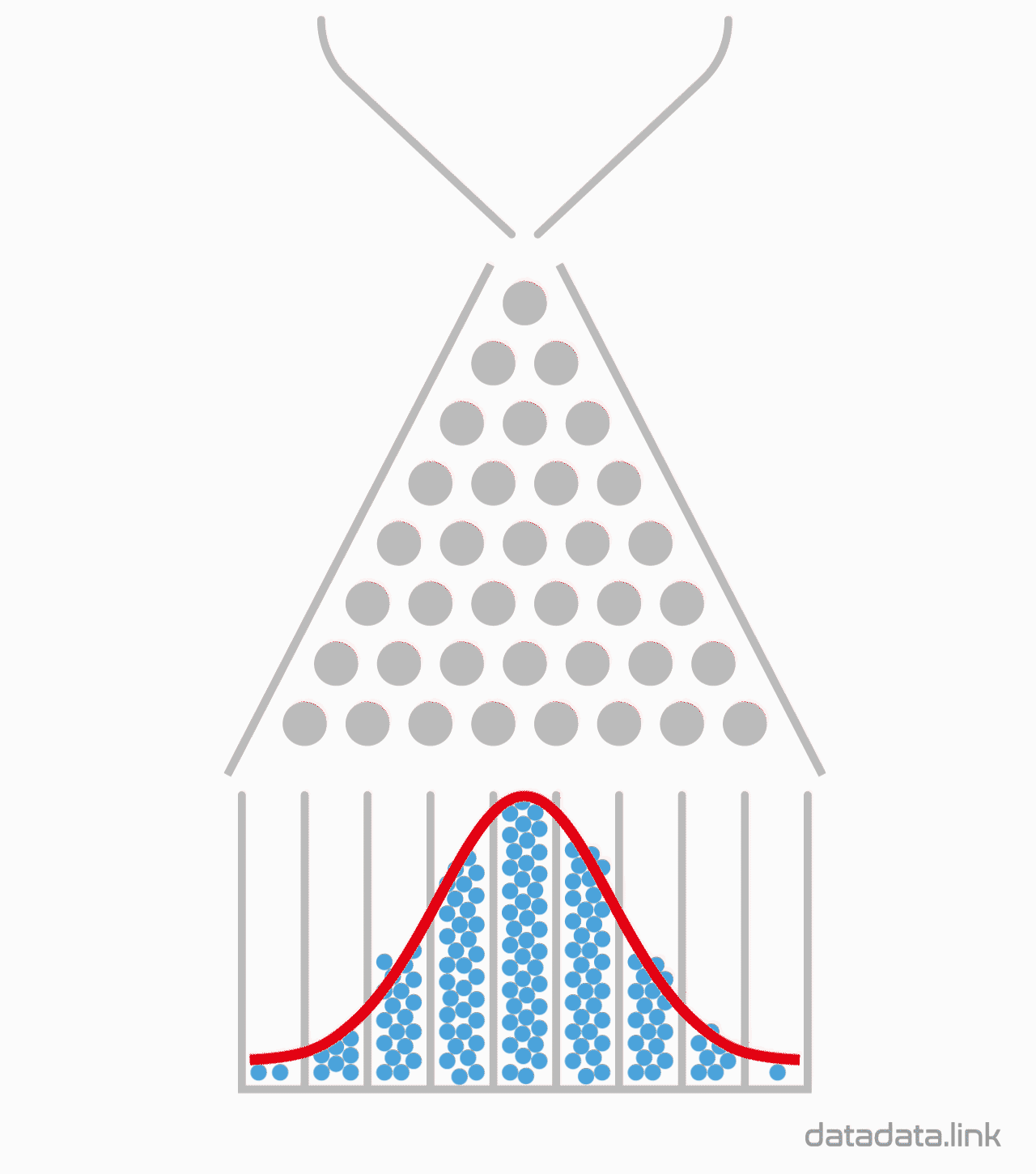
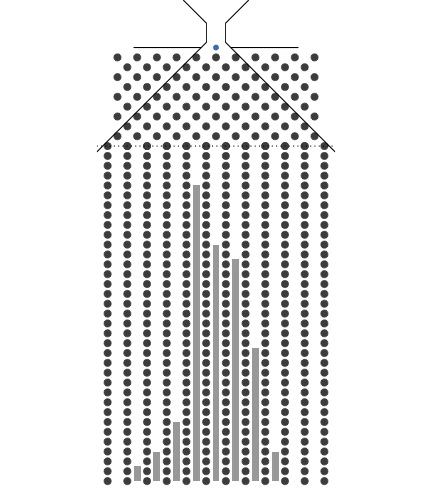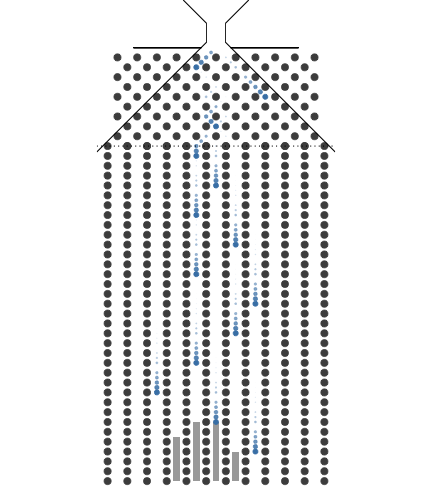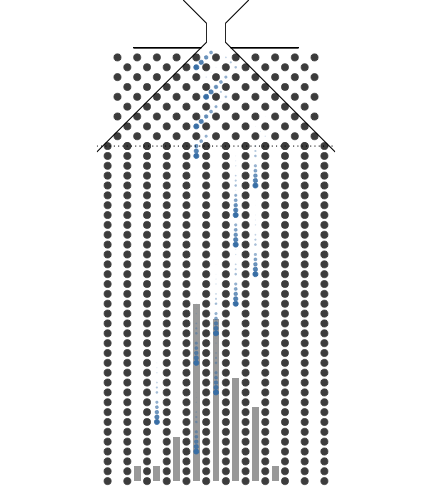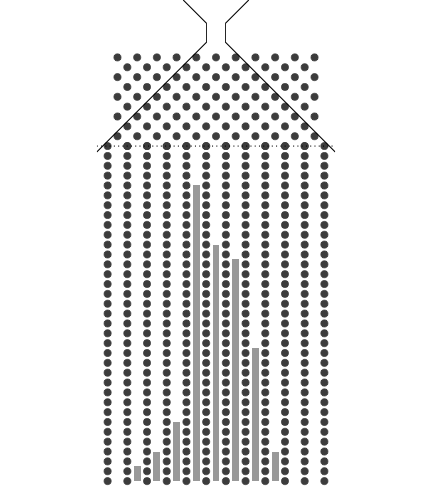
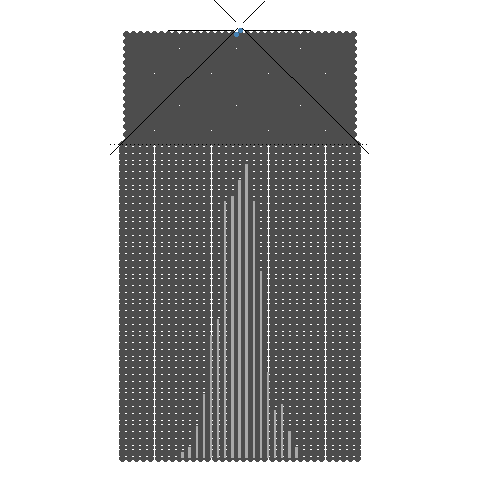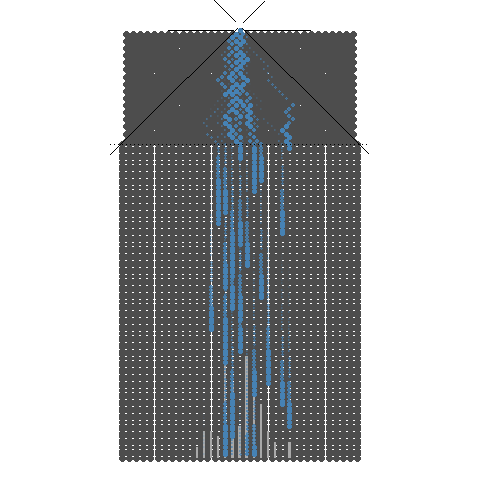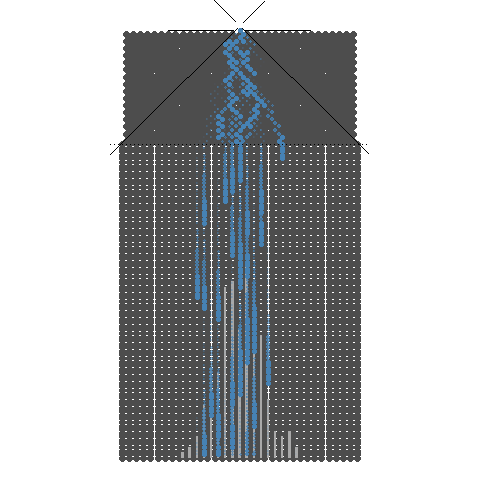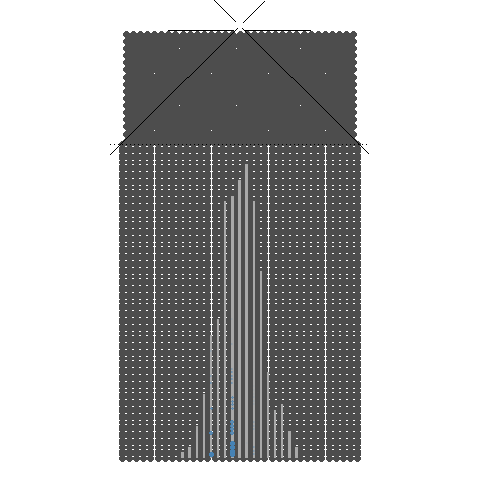
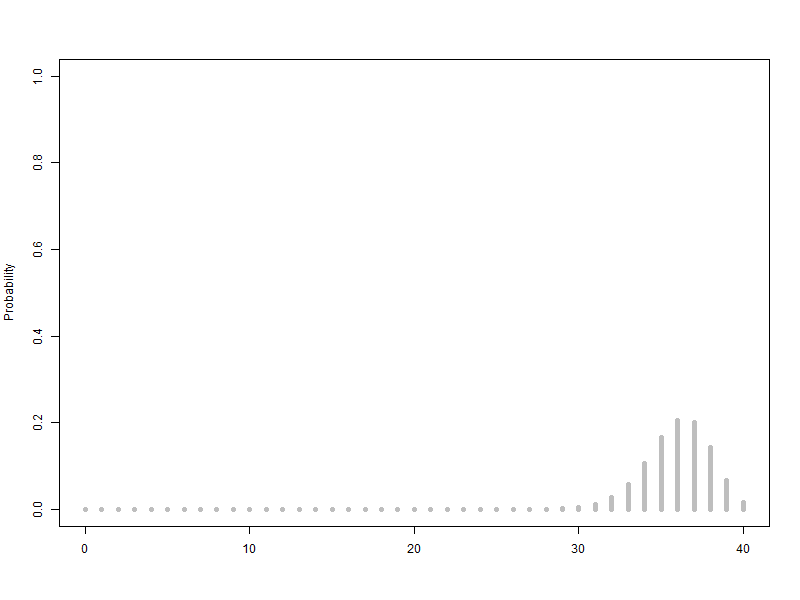
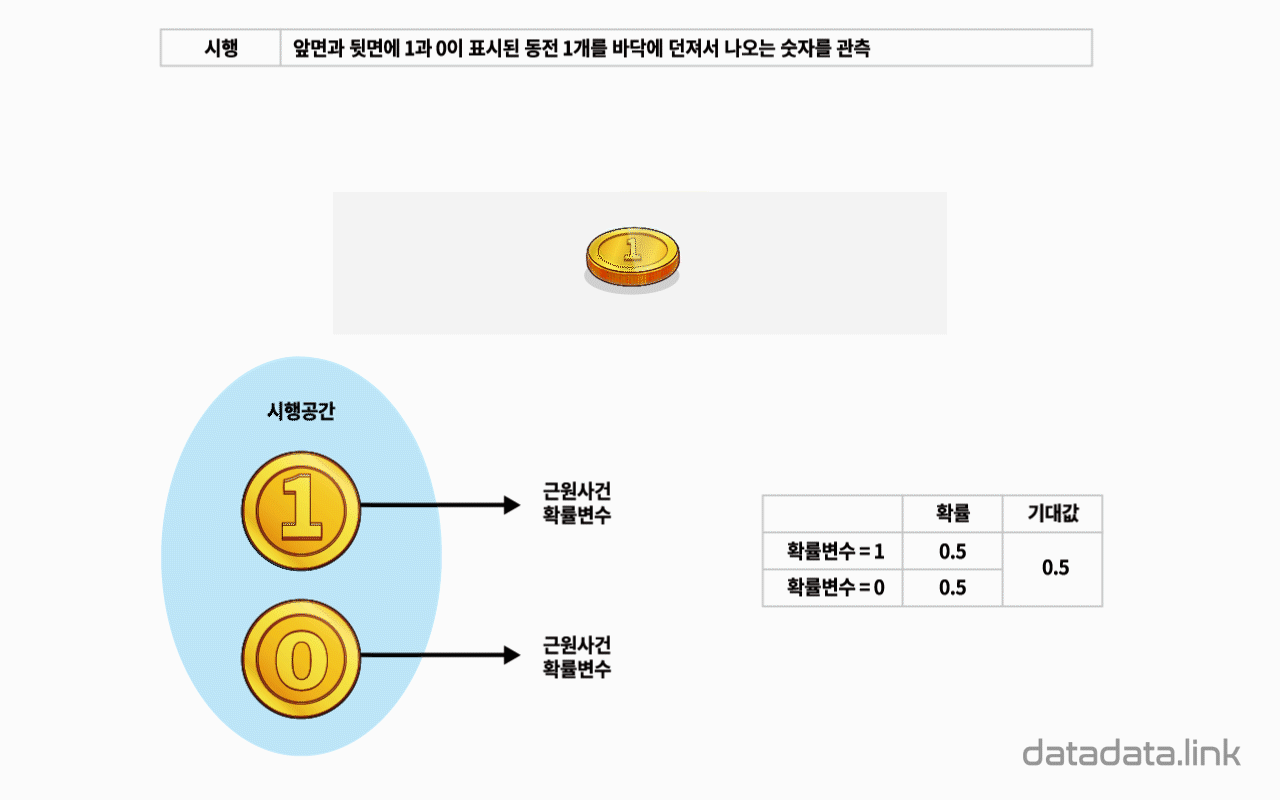
이항분포 ANIMATION : 0과 1의 시행과 확률p를 갖는 시행을 n번하여 그 합을 확률변수로 합니다. 무한번 시행하고 확률을 막대그래프로 표현할 수 있습니다. 이 때 확률변수는양의 정수가 됩니다.
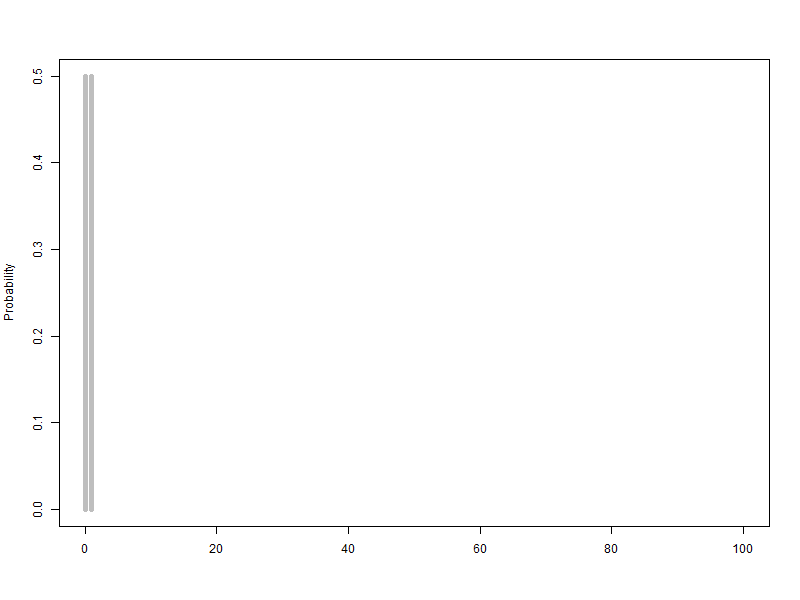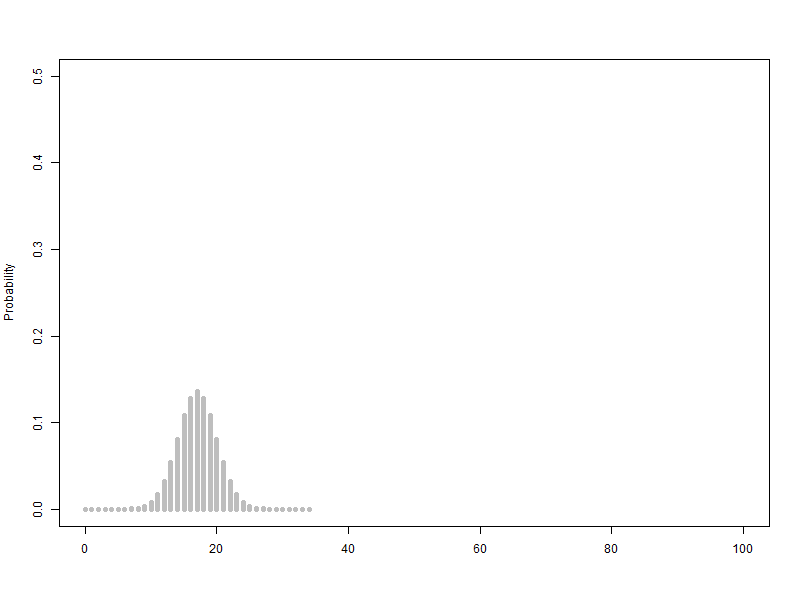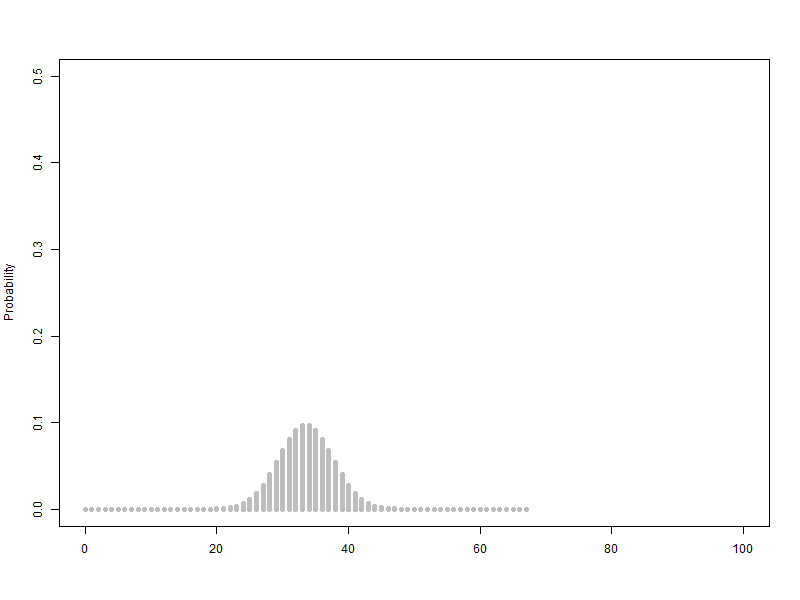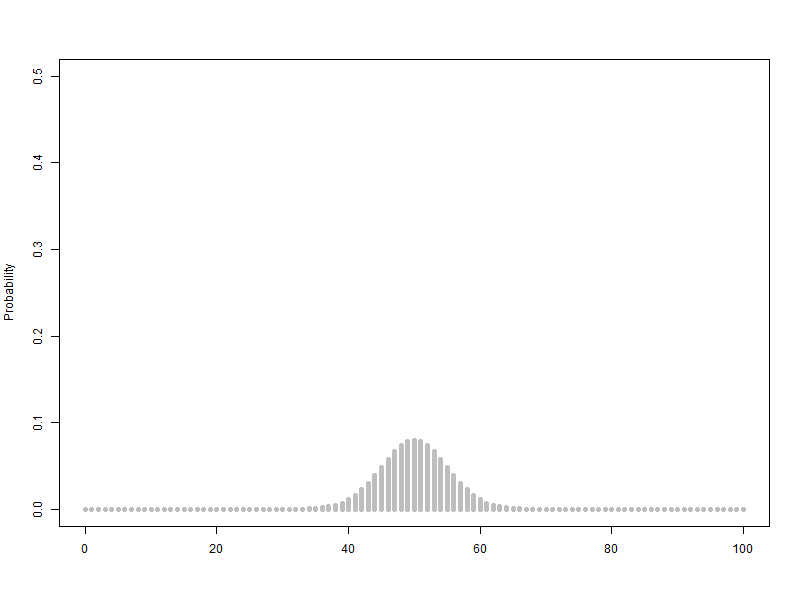
n이 점점 커질때 ( 동전의 개수, 갈톤의 분기점의 개수) -> 이항분포가 정규분포로 근사합니다.
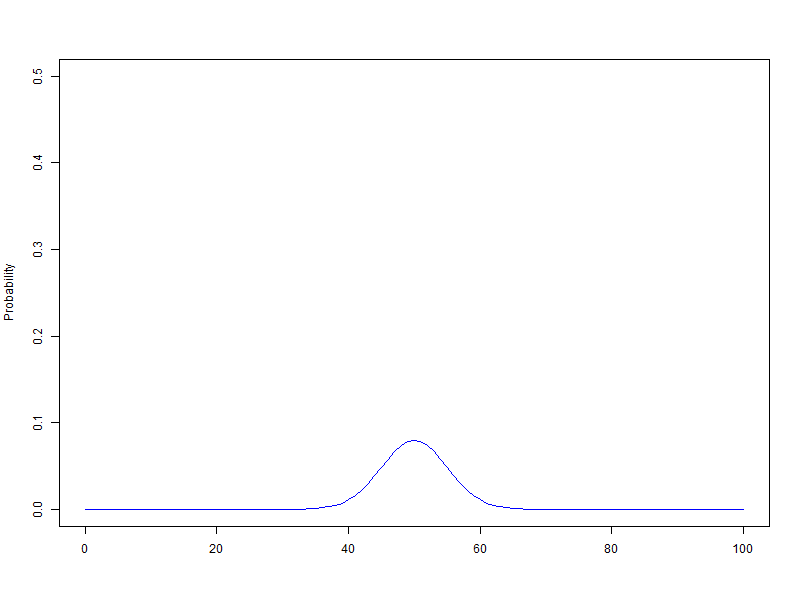
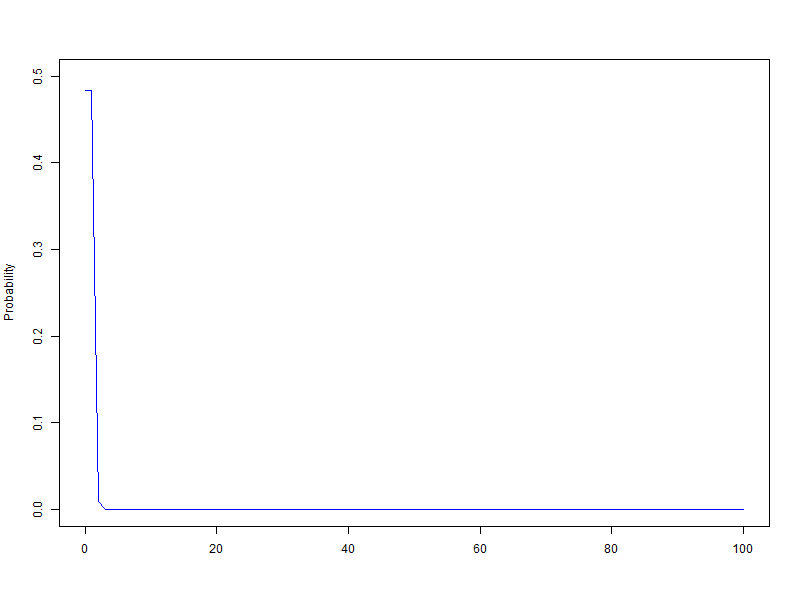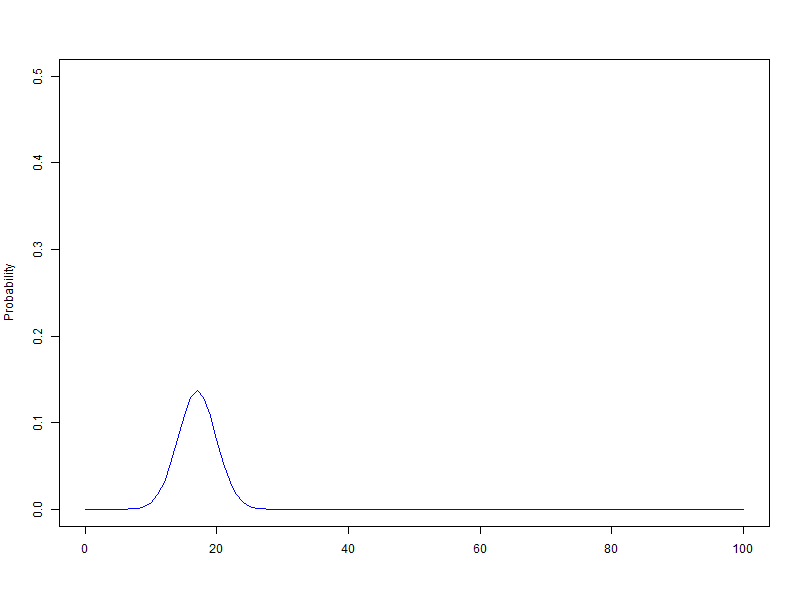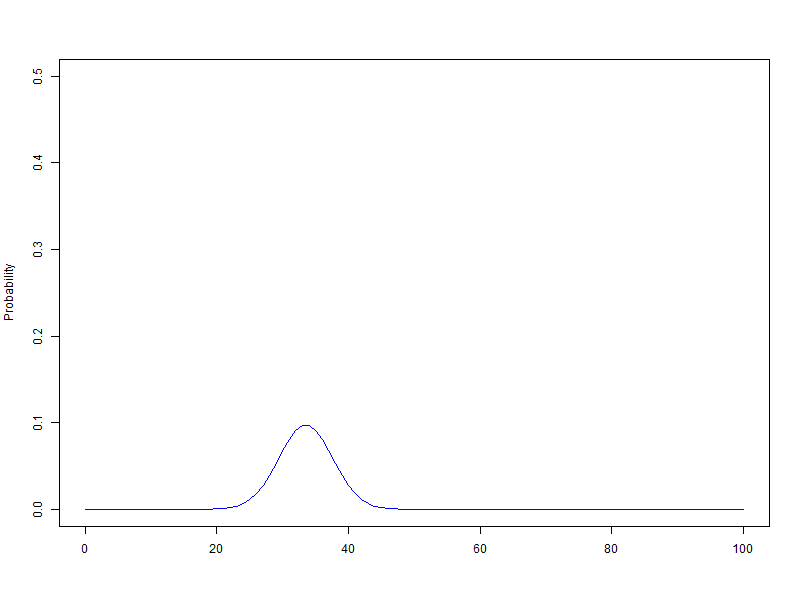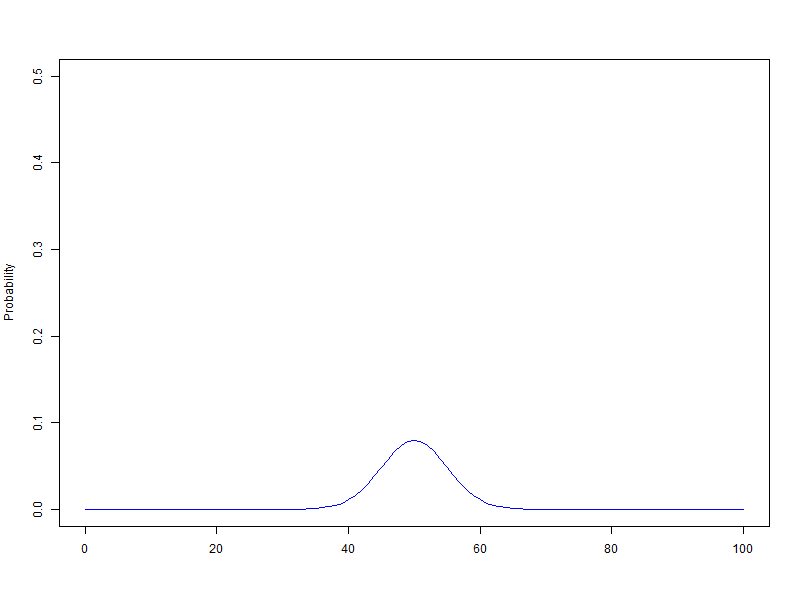
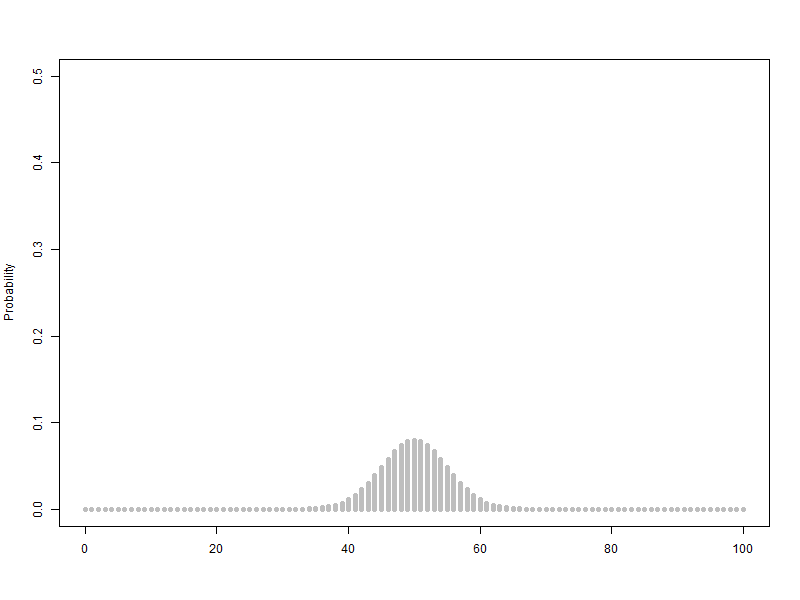
확률변수 단위를 1로하고 범위를 100으로 하여 n을 1에서 100까지 animation, 막대그래프의 범위는 가로축은 0~100, 세로축은 0.5
$B\left({1\sim100,\ 0.5}\right)$
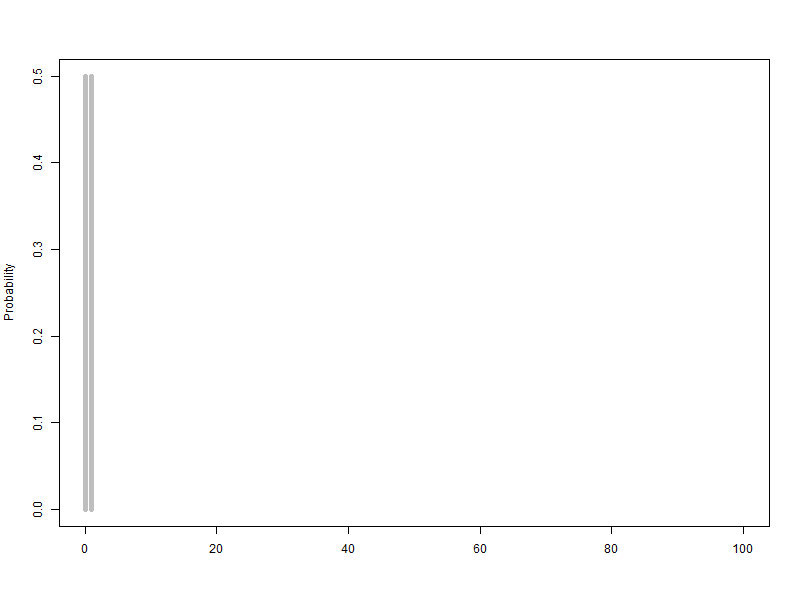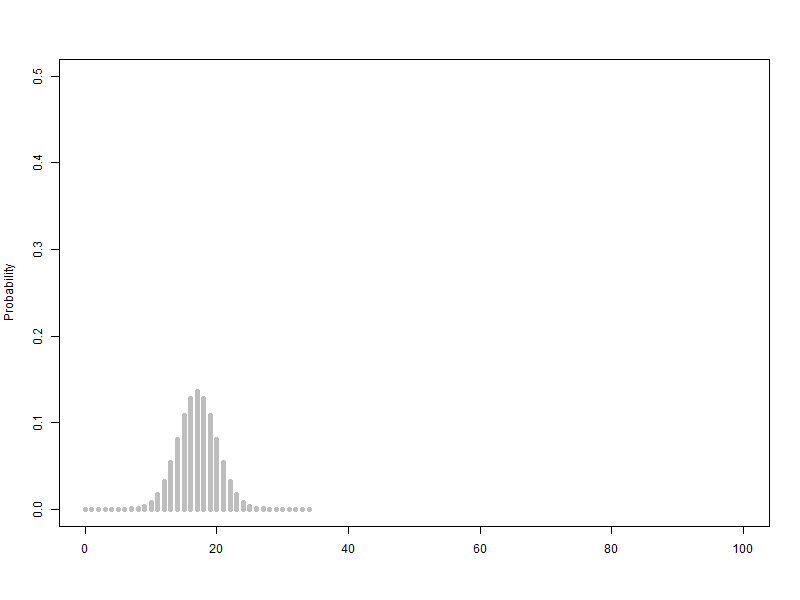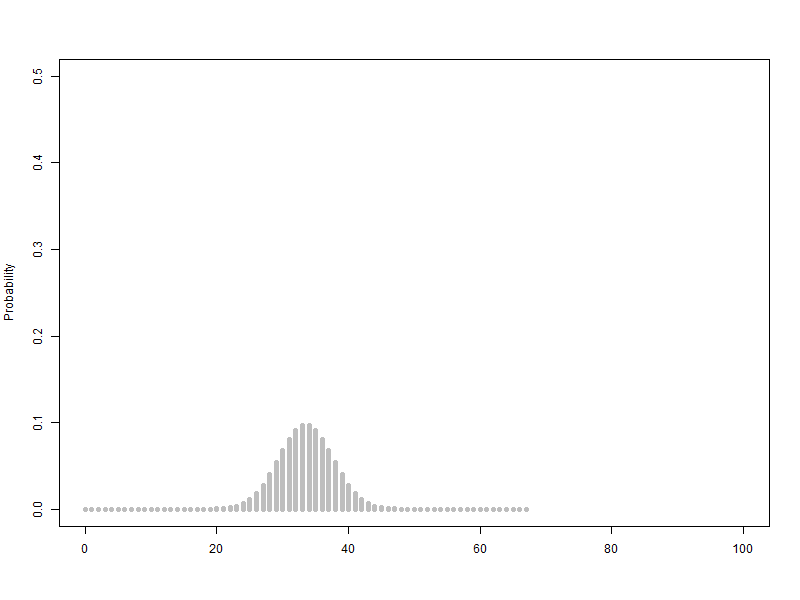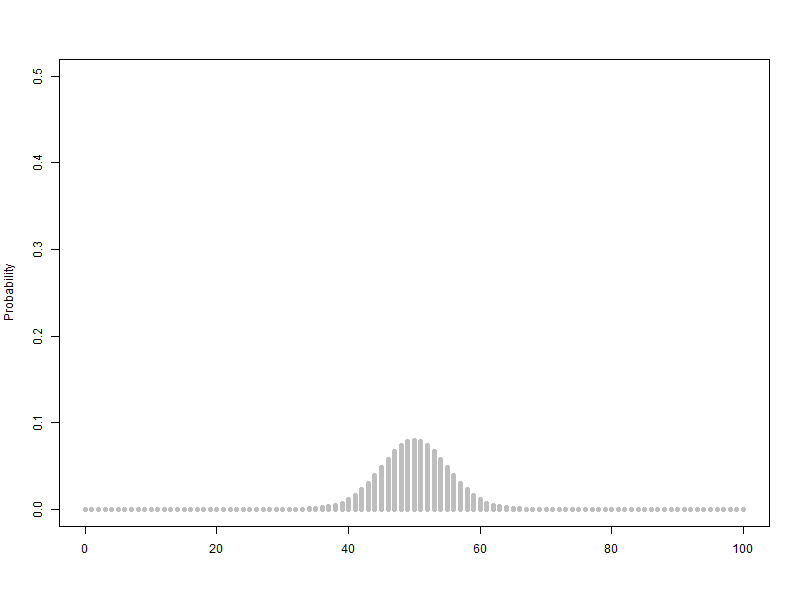
범위를 1로 고정시키고 단위를 1/n 으로 함. n을 1에서 100까지 animation, 막대그래프의 범위는 가로축은 0~1, 세로축은 0.5
$B\left({1\sim{{1}\over{100}},\ 0.5}\right)$
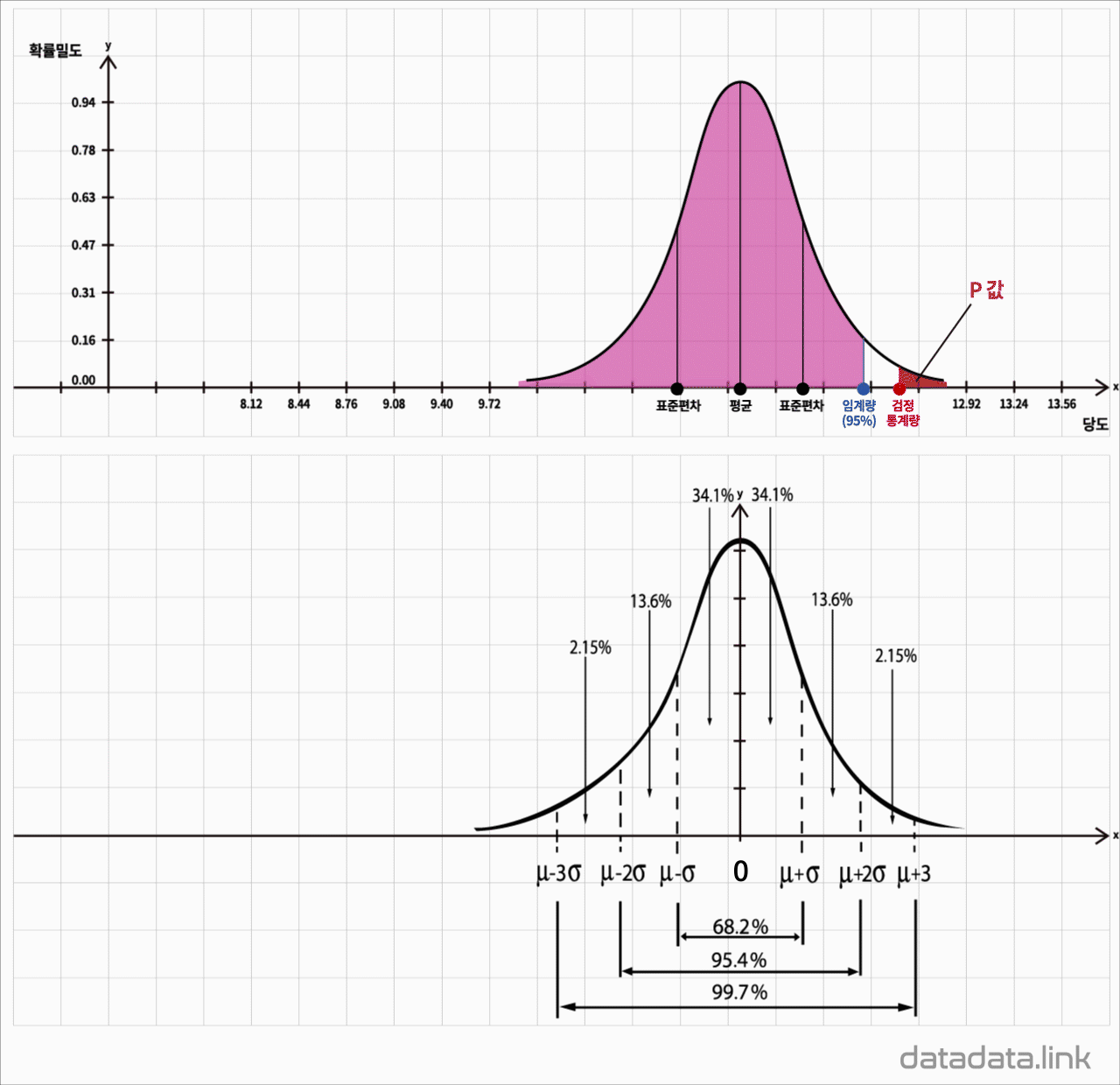
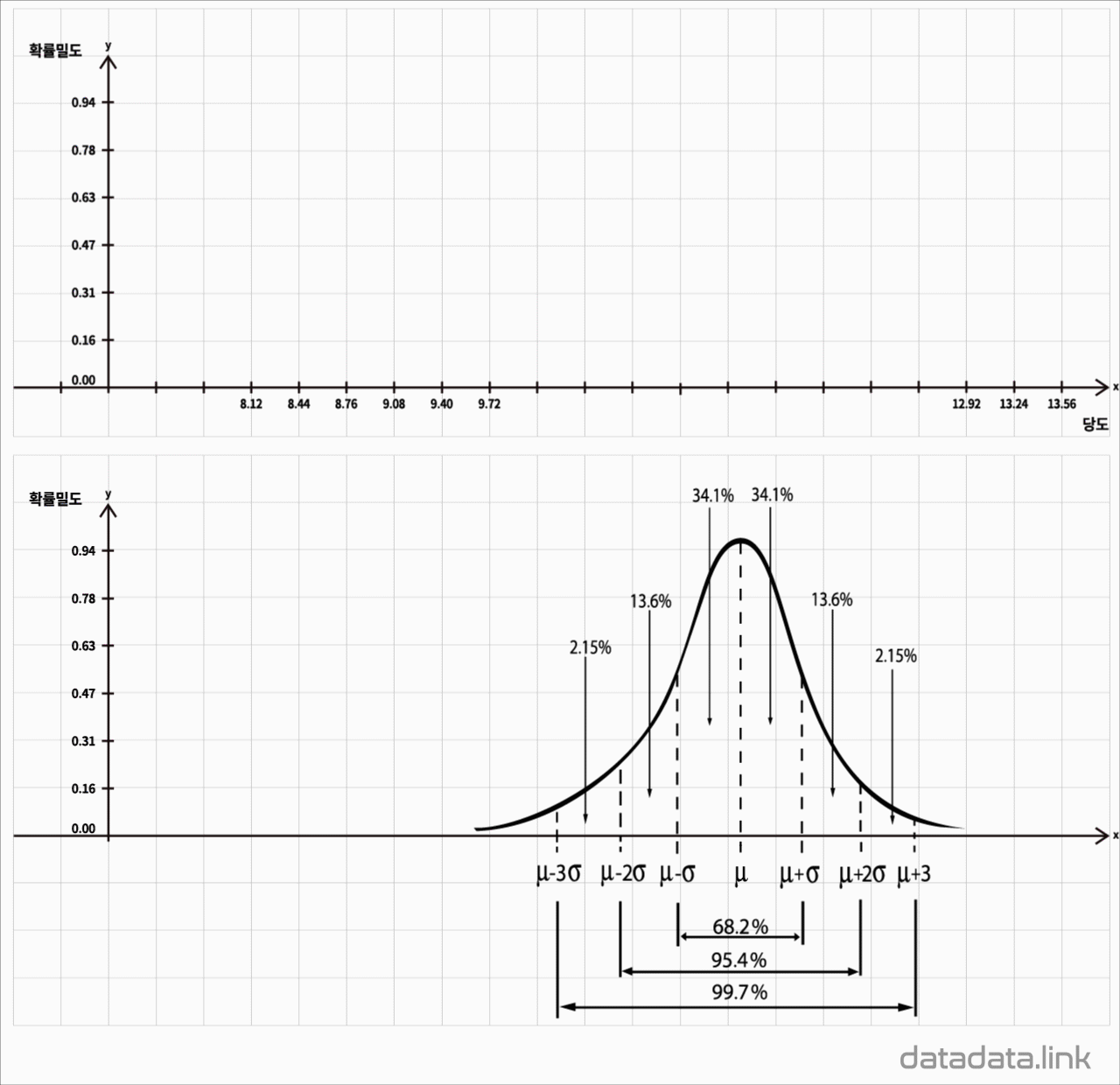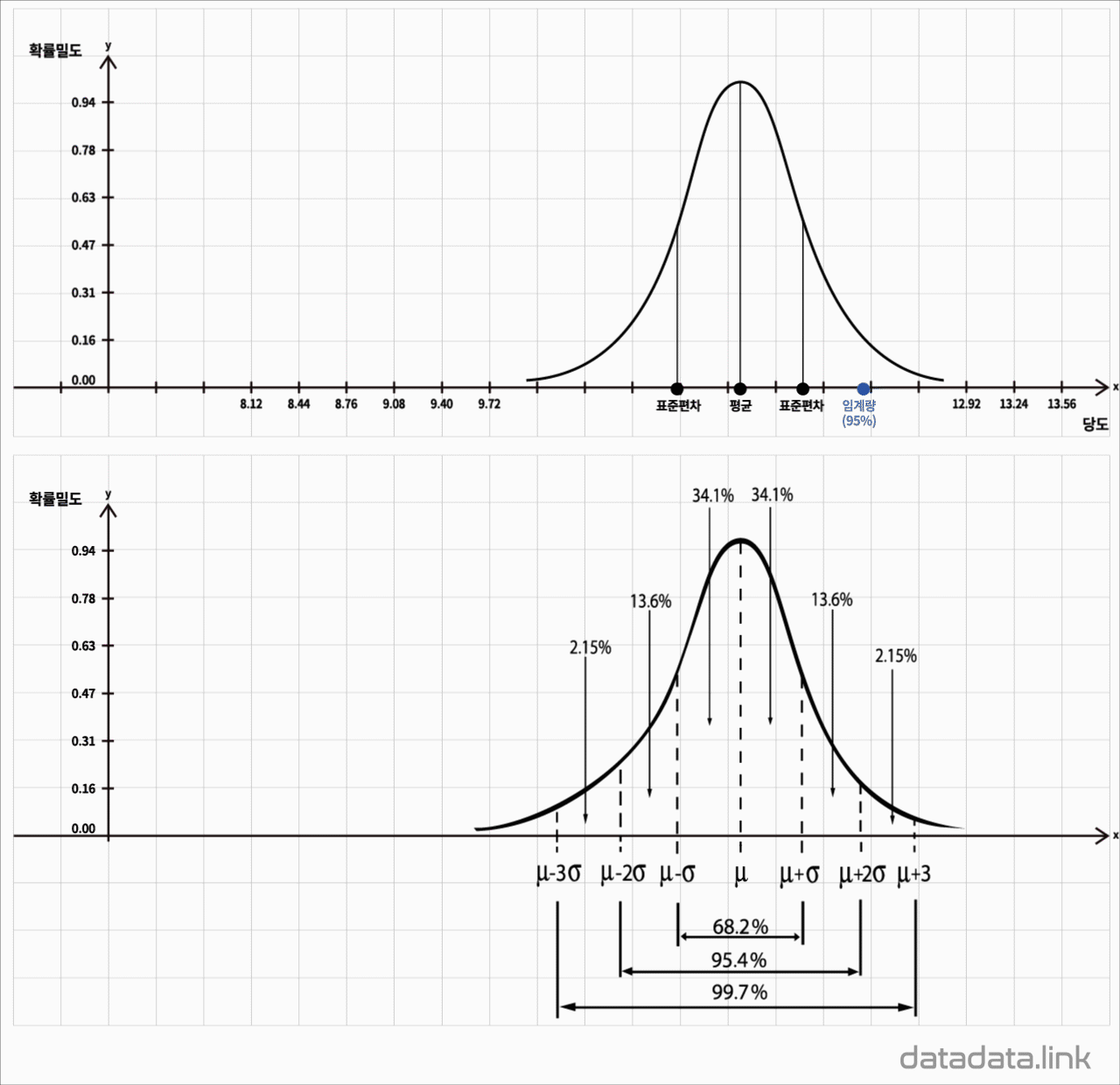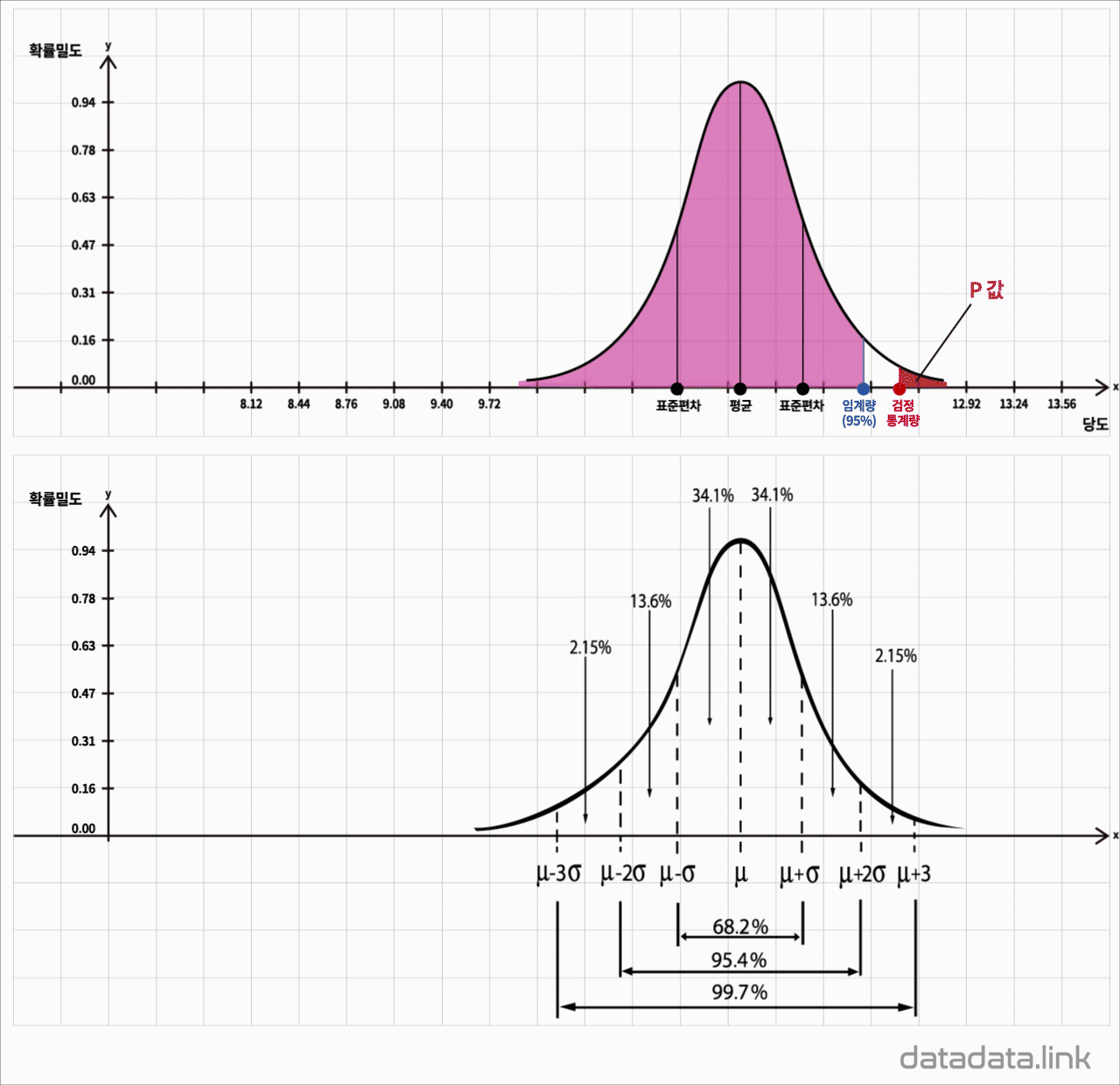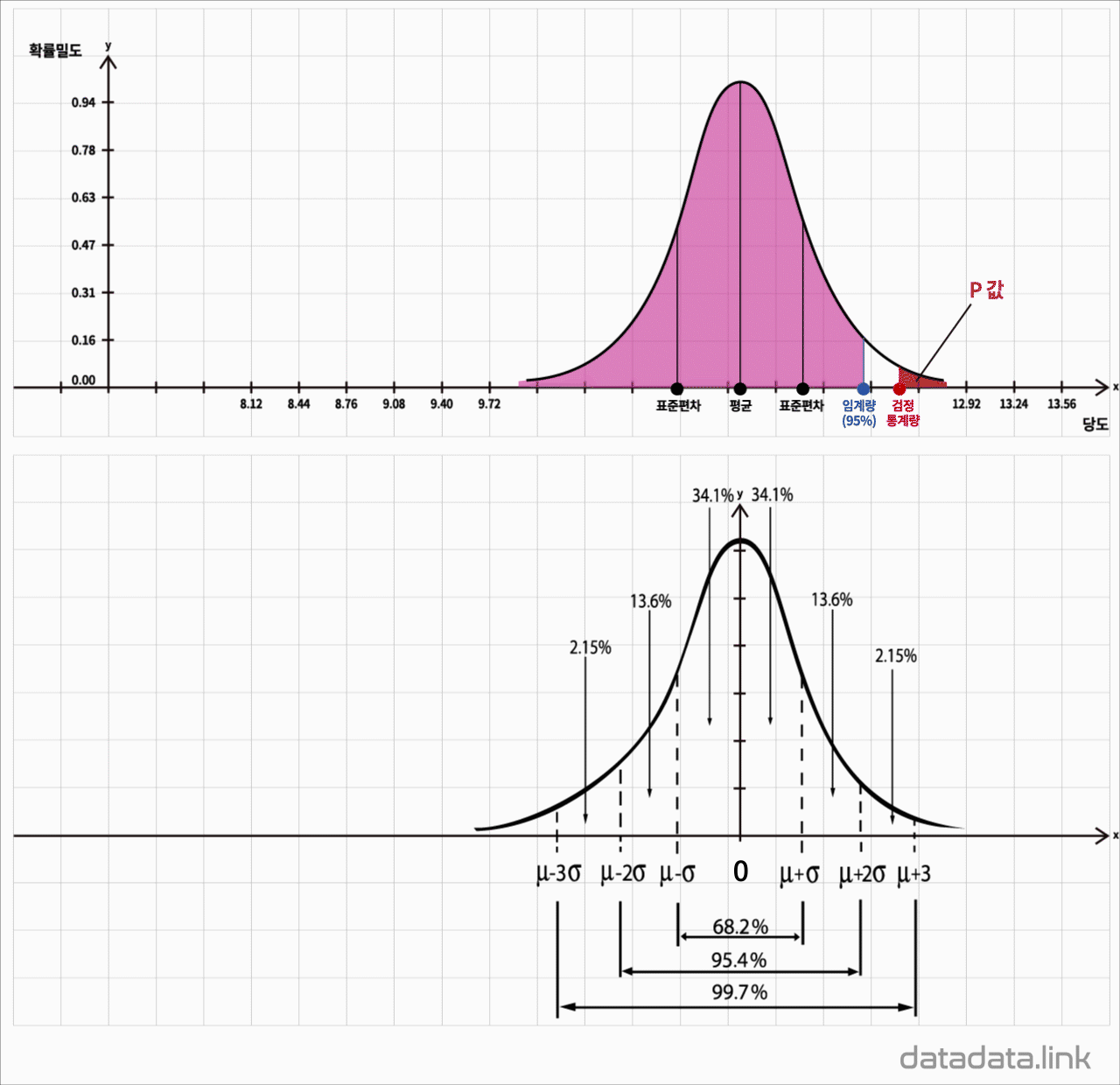
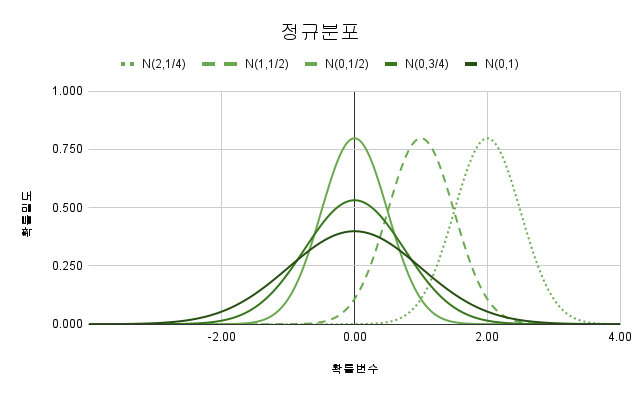
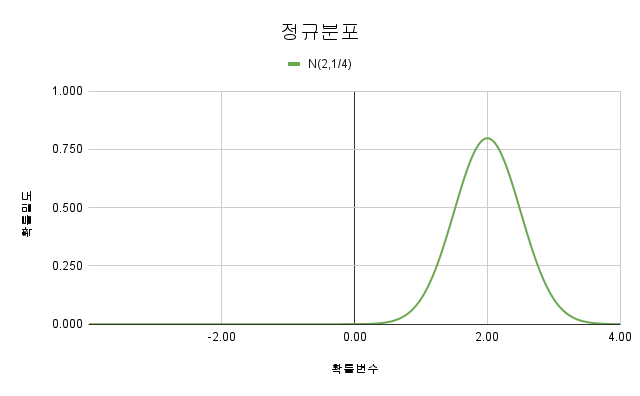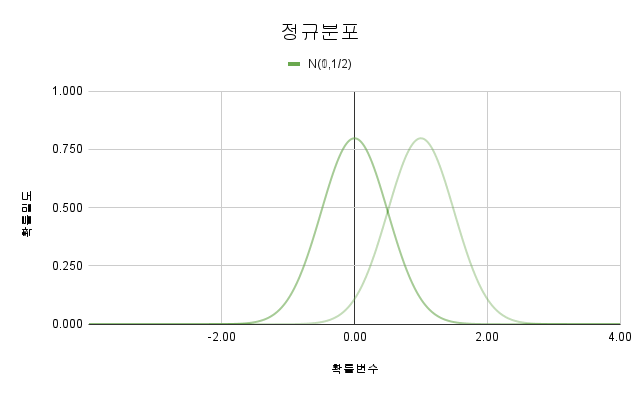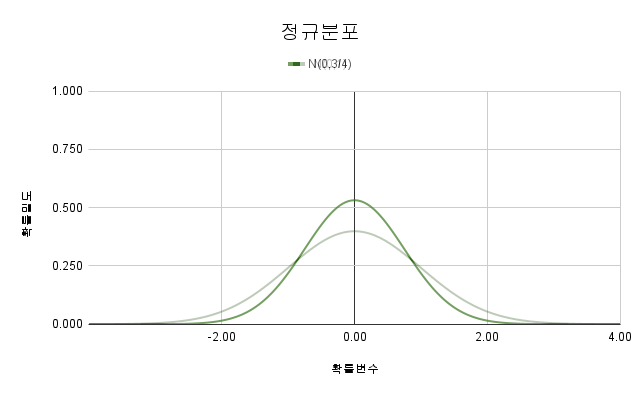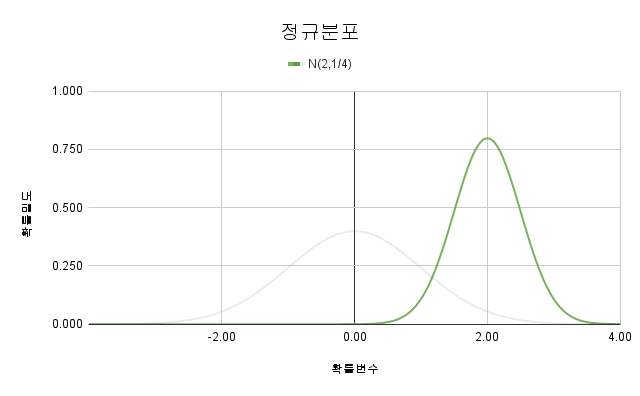
2.3. 정규분포
표준정규분포는 다음과 같습니다.
$y={1\over \sqrt{2\pi}}e^{-{1\over 2}x^2}$
평균 $\mu$와 분산 $\sigma^{2}$ 를 모수로 하고 정규분포를 가지는 모집단의 확률밀도함수입니다.
$f\left({X}\right)={{1}\over{\sqrt{2\pi}\sigma}}e^{-{{{\left({x-\mu}\right)}^{2}}\over{2\sigma^{2}}}},\ -\infty\leq X\leq+\infty$
이항분포
확률변수 $k$가 매개변수 $n$과 $p$를 가지는 이항분포를 따른다면, $k\sim B\left({n,p}\right)$라고 쓴다. $n$번 시행중에 $k$번 성공하는 확률변수의 확률질량함수는
$Pr\left({{K}{=}{k}}\right){=}{f}\left({k;n,p}\right)$
${=}{n \choose k}{p}^{k}{\left({{1}{-}{p}}\right)}^{{n}{-}{k}}$
만약 $X\sim {\rm B}\left({n,p}\right)$라면, $X$의 기대값은
${\rm E}\left[{X}\right]=np$
이고 분산은
$\rm{Var}\left[{X}\right]={\rm E}\left[{X^{2}}\right]-E{\left[{X}\right]}^{2}$
$=np(1-p)$
이항분포 ~ 정규분포
$X\sim {\rm B}\left({n,p}\right)$에서 $n$이 충분히 클 때 $X\sim{\rm N}\left({np,\sqrt{np\left({1-p}\right)}}\right)$로 근사합니다.
$X\sim{\rm N}\left({np,\sqrt{np\left({1-p}\right)}}\right)$
$X\sim {\rm N}\left({\mu ,\sigma^{2}}\right)$
정규분포
표준정규분포
$y=\dfrac{1}{\sqrt{2\pi}}{\rm exp}^{-\dfrac{1}{2}{x^2}}$
평균, $\mu$와 분산, $\sigma^{2}$를 모수로 하는 정규분포를 나타내는 확률변수, $X$의 확률밀도함수 $f(X)$는 다음과 같습니다.
$f(X)=\dfrac{1}{\sigma\sqrt{2\pi}}{\rm exp}^{-\dfrac{1}{2}\dfrac{\left({x-\mu}\right)^2}{\sigma^2}}$
여기서, $-\infty\leq X\leq+\infty$
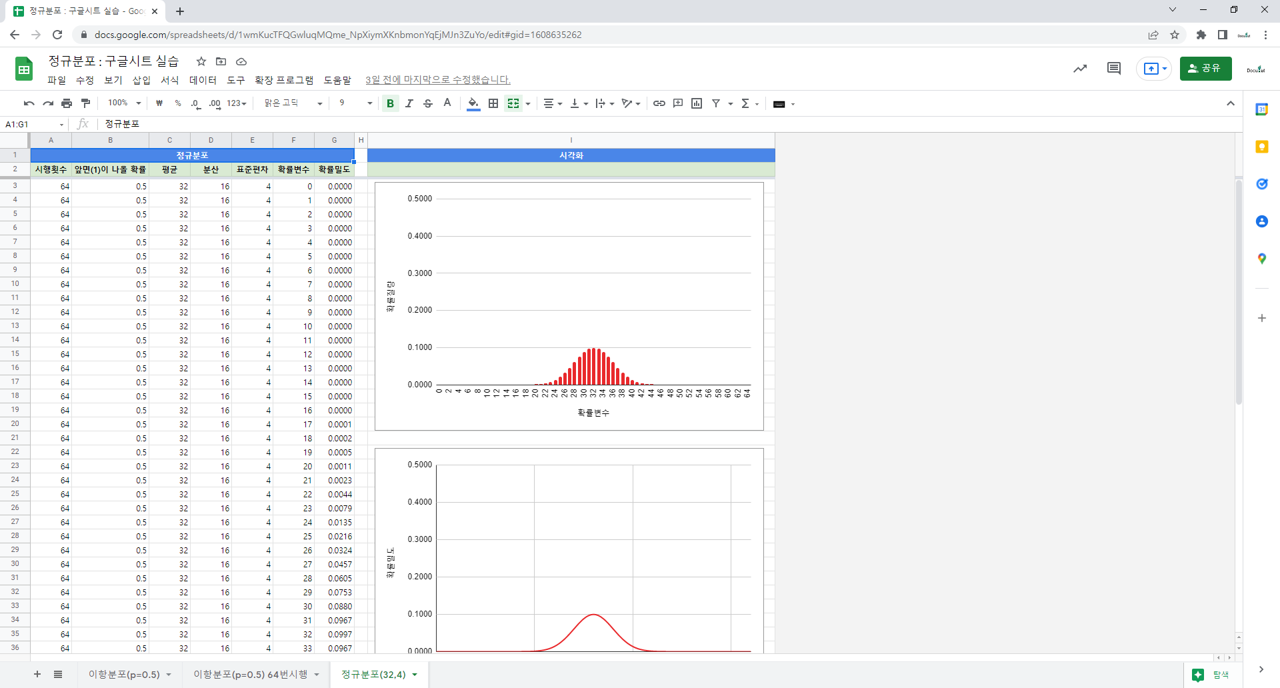
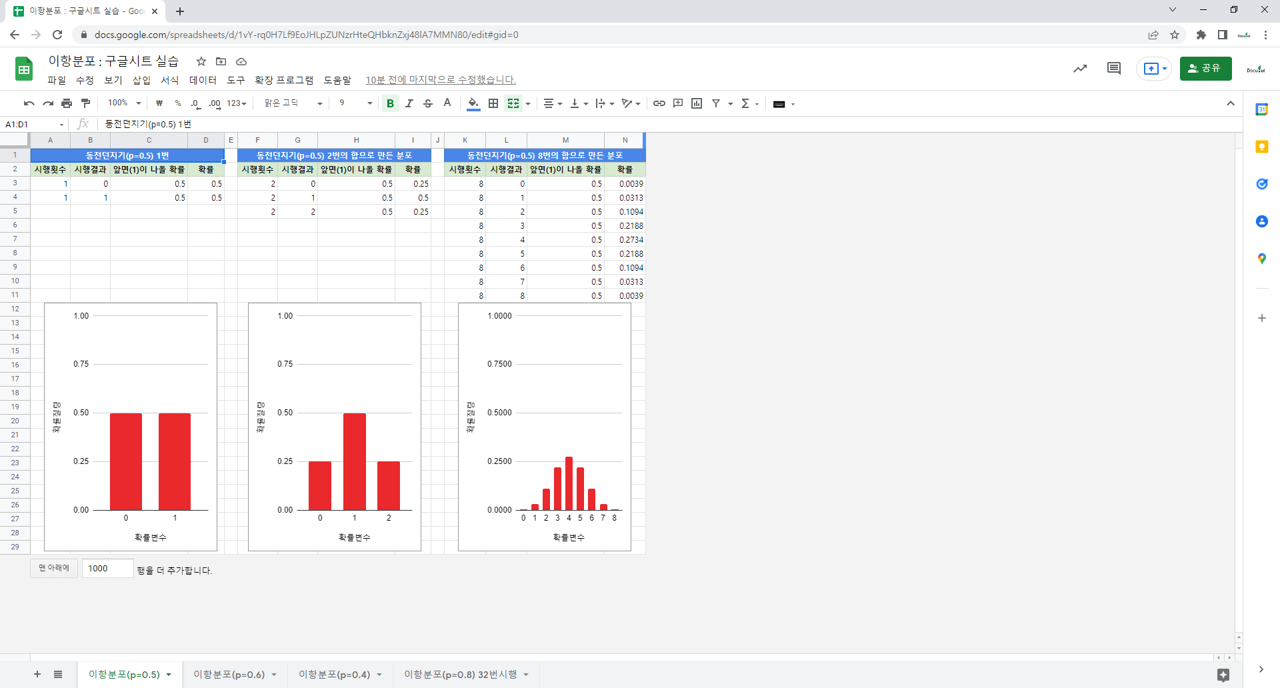
3. 실습
3.2. 함수
=FACT(A3) : 숫자의 계승. A3에 있는 숫자의 계승을 계산함. 예를 들어, A3에 있는 숫자가 2이면, 2×1(2곱하기 1)의 값을 계산해서 표시함. A3에 있는 숫자가 3이면, 3×2×1(3곱하기2곱하기 1)의 값을 계산해서 표시함.
=POWER(C3,B3) : 거듭제곱. C3의 값을 B3의 값만큼 거듭제곱한 값을 계산해서 표시함.
=SQRT(D3) : 제곱근. D3에 있는 값의 제곱근을 계산해서 표시함.
=NORMDIST(F3,C3,E3,FALSE) : 정규분포 확률밀도. C3가 평균, E3가 표준편차인 정규분포에서 F3가 확률변수일때의 확률밀도를 계산해서 표시함. FALSE를 TRUE로 변경하면 누적확률밀도를 계산해서 표시함.
3.3. 실습강의
– 동전던지기
– 동전던지기 결과의 합
– 이항분포
– 정규분포