단순선형회귀분석 – 회귀직선 : 독립표본 구간추정
애니메이션 그림 단순선형회귀모형 사례 단순선형회귀모형 사례 단순선형회귀분석 단순선형회귀모형 사례 단순선형회귀모형 사례 단순선형회귀분석 단순선형회귀모형 사례 단순선형회귀모형 사례 단순선형회귀분석 단순선형회귀모형 사례 단순선형회귀모형 사례 단순선형회귀분석 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1.단순선형회귀(Simple linear regression) 모형 사례 단순선형회귀(simple linear regression) 모델은 요인변수(factor, 설명변수, 독립변수)가 연속형인 경우의 […]
원점을 지나는 단순선형회귀모형 – 회귀직선 : 단일표본 구간추정
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 준비 중입니다. 주제어 1.제목 원점을 지나는 단순선형회귀모형은 다음식으로 나타냅니다. $Y_{i}=beta_{1}X_i+epsilon_{i}$$ $$bf{Y}{=}bf{X}boldsymbol{beta}{+}boldsymbol{mathit{epsilon}}$$ $bf{Y}=left[{begin{array}{c}{{Y}_{1}}\{{Y}_{2}}\{vdots}\{{Y}_{n}}end{array}}right]$, $bf{X}=left[{begin{array}{cc}{1}&{{X}_{1}}\{1}&{{X}_{2}}\{vdots}&{vdots}\{1}&{{X}_{n}}end{array}}right]$, $boldsymbol{beta}=left[{begin{array}{c}{{beta}_{0}}\{{beta}_{1}}end{array}}right]$, $boldsymbol{epsilon}=left[{begin{array}{c}{{epsilon}_{1}}\{{epsilon}_{2}}\{vdots}\{{epsilon}_{n}}end{array}}right]$ 여기서, $i$는 $1, … , n$ $beta_0=0$ $n$은 집단의 크기 원점을 지나는 중선형회귀모형은 다음식으로 나타냅니다. $$Y_{i}=beta_{1}X_{i1}+cdots+beta_{k}X_{ik}+epsilon_{i}$$ $$bf{Y}{=}bf{X}boldsymbol{beta}{+}boldsymbol{mathit{epsilon}}$$ $bf{Y}=left[{begin{array}{c}{{Y}_{1}}\{{Y}_{2}}\{vdots}\{{Y}_{n}}end{array}}right]$, $bf{X}=left[{begin{array}{ccccc}{1}&{{X}_{11}}&{{X}_{12}}&{cdots}&{{X}_{1k}}\{1}&{{X}_{21}}&{{X}_{22}}&{cdots}&{{X}_{2k}}\{vdots}&{vdots}&{vdots}&{ddots}&{vdots}\{1}&{{X}_{n1}}&{{X}_{n2}}&{cdots}&{{X}_{nk}}end{array}}right]$, $boldsymbol{beta}=left[{begin{array}{c}{{beta}_{0}}\{{beta}_{1}}\{vdots}\{{beta}_{k}}end{array}}right]$, $boldsymbol{epsilon}=left[{begin{array}{c}{{epsilon}_{1}}\{{epsilon}_{2}}\{vdots}\{{epsilon}_{n}}end{array}}right]$ 여기서, $i$는 $1, […]
위치와 양을 비교하는 가설의 검정은?
목차 평균은 위치이고 분산은 양이며, 평균의 비교는 t검정으로 분산의 비교는 F검정으로 행합니다. 1. 위치와 양의 가설검정 위치(位置, position)를 다루는 학문은 기원전 3000년경에 시작된 기하학(geometry)입니다. 양(量, quantity)을 다루는 학문은 기원전 2000년경 이후 성립된 산술(arithmetic)입니다. 이산형(discrete type) 데이터인 경우에도 평균/분산이라는 모수 개념이 성립하지만, 본질적으로 연속형(continuous type) 데이터에서 의미가 명확합니다. 연속형 데이터인 경우에 “평균”, “분산” 이라는 모수(parameter)를 부여하는 […]
여러 범주형 확률변수가 생성하는 항목 간 조건부 확률분포 비교: 연관분석 카이제곱검정
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 통계량을 통한 모수 추정에서, 확률변수의 모평균, 모분산, 모표준편차는 각각 표본평균, 표본분산, 표본표준편차를 통해 추정됩니다. 상관분석은 두 변수 간의 선형적 관계를 측정하며, 피어슨상관계수는 이 관계의 강도와 방향을 수치화합니다. 공분산은 두 변수 간의 변동성을 나타내며, 상관계수는 공분산을 표준화한 값입니다. […]
단순선형회귀에서 오차의 분산이 작아지면 종속변수와 독립변수의 분산의 비는 무엇과 같아지나?
목차 기울기의 제곱과 같아집니다. 오차가 거의 없어진다면, 종속변수 $Y$ 의 변동성은 거의 전적으로 독립변수 $X$에 의해 설명됩니다. 이때 분산의 비는 바로 기울기의 제곱과 같아집니다. [dfrac{mathrm{Var}(Y)}{mathrm{Var}(X)} to beta_1^2 quad text{as } sigma^2 to 0] 단순선형회귀에서 오차항의 표준편차가 작아지면 종속변수와 독립변수의 표준편차의 비는 기울기와 같아집니다. [frac{mathrm{SD}(Y)}{mathrm{SD}(X)} to |beta_1| quad text{as } sigma to 0] 1. 단순선형회귀모델의 분산 관계 […]
두 연속형 확률변수의 회귀계수 비교: 회귀분석 t검정
애니메이션 그림 목차 요약영상 1 Videos 준비중 0:03 저자정보 출판이력 DOI 인용 다운로드 Print 구글문서 Print 구글문서 요약 통계량을 통한 모수 추정에서, 확률변수의 모평균, 모분산, 모표준편차는 각각 표본평균, 표본분산, 표본표준편차를 통해 추정됩니다. 상관분석은 두 변수 간의 선형적 관계를 측정하며, 피어슨상관계수는 이 관계의 강도와 방향을 수치화합니다. 공분산은 두 변수 간의 변동성을 나타내며, 상관계수는 공분산을 표준화한 값입니다. […]
일원분산분석에서 F통계량, F검정통계량, F검정통계값의 관계는?
CONTENTS 귀무가설을 통해 , F통계량의 변수의 수를 줄여 F검정통계량을 구합니다. 여기서, 귀무가설은 알 지 못하는 모수에 대한 가설입니다. F검정통계량은 확률변수이며 정의된 확률분포함수로 표현합니다. 표본데이터를 통해, F검정통계량의 함수값인 F검정통계값을 구합니다. 일원분산분석에서 F통계량 일원분산분석에서의 F통계량을 함수로 보면 다음과 같이 표현할 수 있습니다. $$F(chi^2_B, df_B, chi^2_W, df_W) = dfrac{dfrac{chi^2_B}{df_B}}{dfrac{chi^2_W}{df_W}}= dfrac{dfrac{S_{B}^2}{sigma_{B}^2}}{dfrac{S_{W}^2}{sigma_{W}^2}}$$ 여기서, $chi^2_B$는 표본내 집단의 카이제곱: $chi^2_B=df_Bdfrac{S_B^2}{sigma_B^2}$ $chi^2_W$는 표본내 […]
t통계량, t검정통계량, t검정통계값의 관계는?

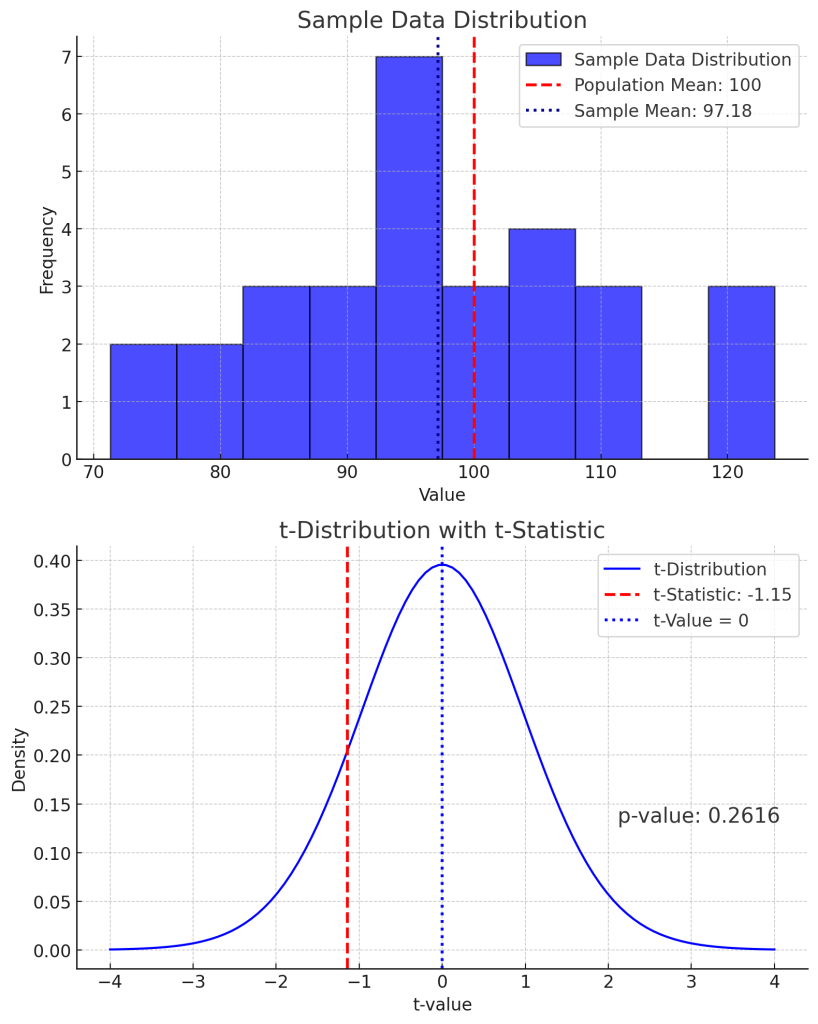
CONTENTS 귀무가설을 통해 , t통계량의 변수의 수를 줄여 t검정통계량을 구합니다. 여기서, 귀무가설은 알 지 못하는 모수에 대한 가설입니다. t검정통계량은 확률변수이며 정의된 확률분포함수로 표현합니다. 표본데이터를 통해, t검정통계량의 함수값인 t검정통계값을 구합니다. t통계량, t검정통계량, t검정통계값의 관계 t통계량을 함수로 보면 다음과 같습니다. $$t(bar{X}, mu, s, n) = dfrac{bar{X} – mu}{dfrac{s}{sqrt{n}}}$$ 여기서, $t$는 t통계량 $nu$는 자유도: $nu=n-1$ $n$은 표본크기 $Gamma(,,,)$는 […]
모분산을 알고 표본크기가 작은 경우, Z검정과 t검정 중, 어느 검정?

CONTENTS Z검정입니다. Z검정과 t검정은 확률변수가 정규분포를 따르거나 표본크기가 30이상인 경우에 사용합니다. 확률변수가 정규분포를 따르지 않고 표본크기가 30미만인 경우는 비모수검정을 사용합니다. Z검정은 모분산을 아는 경우에 사용 모분산이 알려진 경우에는 표본크기와 관계없이 Z검정을 사용합니다. 모분산을 알면 모집단의 실제 변동성을 직접 반영할 수 있습니다. 따라서 자유도에 따른 보정이 필요하지 않습니다. 그러나 모분산을 아는 경우는 현실적으로 거의 없습니다. 모분산을 […]
검정통계량(Test statistic)은 확률변수?
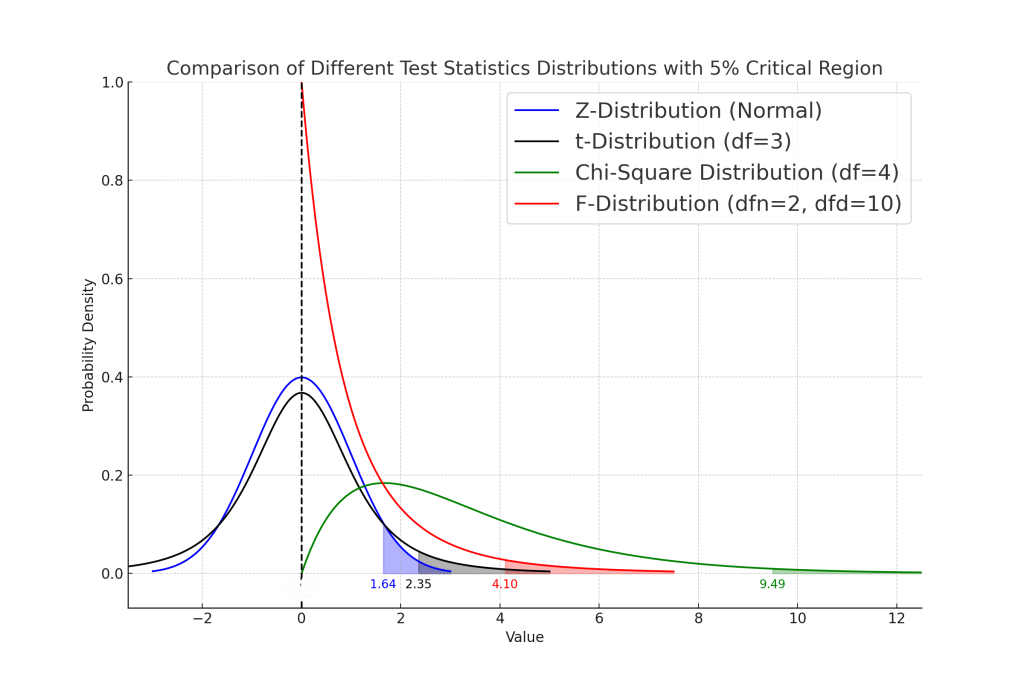
CONTENTS 네, 검정통계량은 확률분포를 가지는 확률변수입니다. 무작위 표본으로부터 계산되는 통계량이기 때문입니다. 검정통계량은 무엇? 검정통계량은 주어진 표본 데이터에서 계산되는 통계량 중 하나입니다. 이 통계량은 모집단의 모수를 추정하거나 가설을 검정하는 데 사용되어 검정통계량이라고 부릅니다. 검정통계량은 특정 확률변수를 검정의 종류에 따른 확률분포의 확률변수로 변환하는 식이며, 이는 표본의 구성이나 크기에 따라 달라집니다. 예를 들어, t검정에서 사용되는 t통계량은 표본의 표본평균 […]

