설향이라는 우리나라의 대표적인 딸기 품종이 있습니다.

이 품종의 당도 평균을 알고 싶은데, 모든 설향을 다 측정할 수는 없어서, 스무알만 추출해서 당도를 측정해보았습니다.

설향 스무알의 당도 평균은 11.56, 분산 0.21, 표준편차 0.46이 나왔습니다.

그런데, 이 샘플로부터 얻은 평균을 전체 평균과 동일하다고 단언하기가 힘들어서, 95% 신뢰구간으로 표현해 보았습니다.

11.35 ~ 11.76

그럼, 전체 설향 중 95%의 당도는 이 범위 내에 있을까요?

이 신뢰구간은 다음의 가정을 내포하고 있습니다.

우리가 설향 스무알을 추출한 방식이 랜덤해야 합니다. 

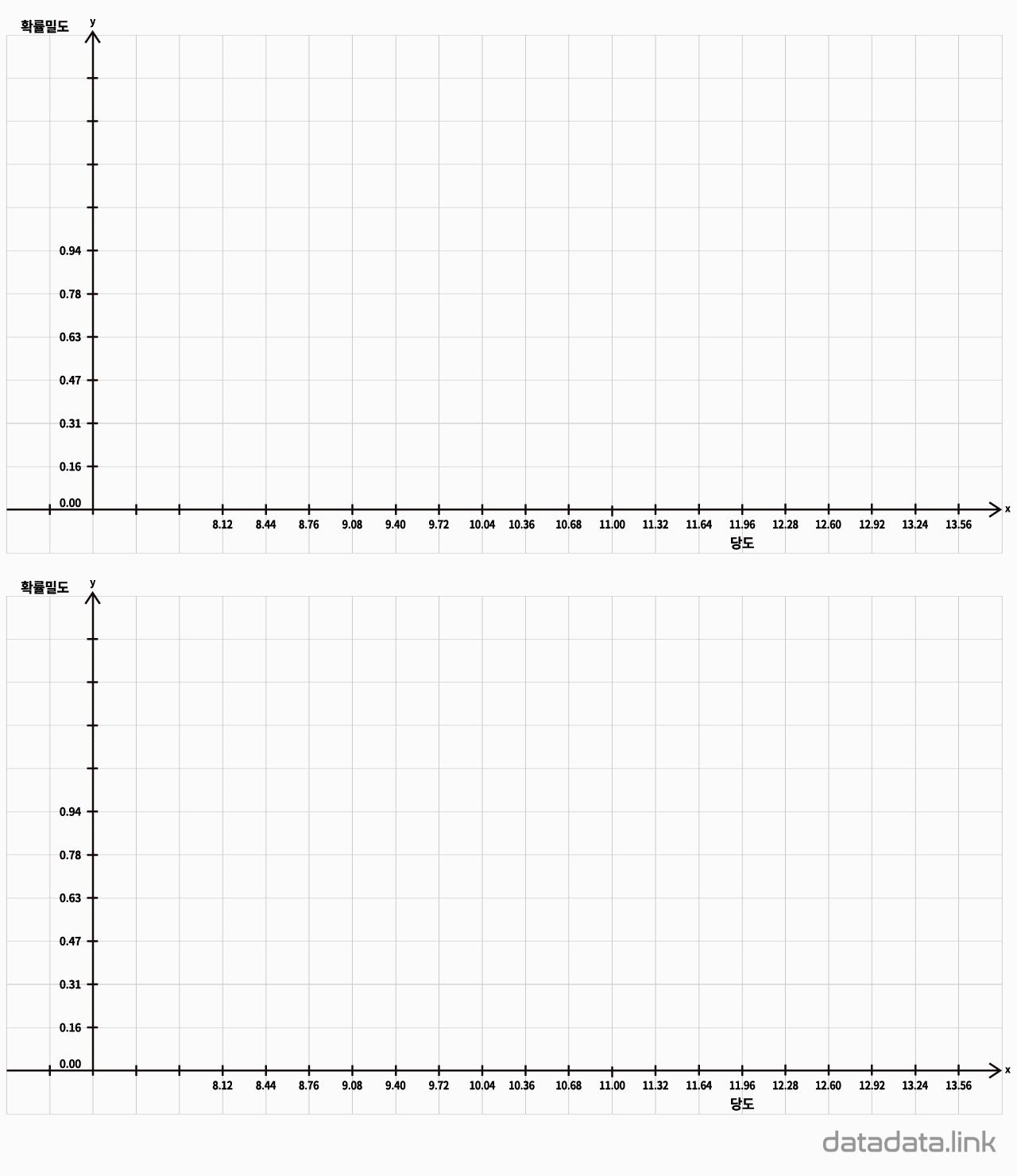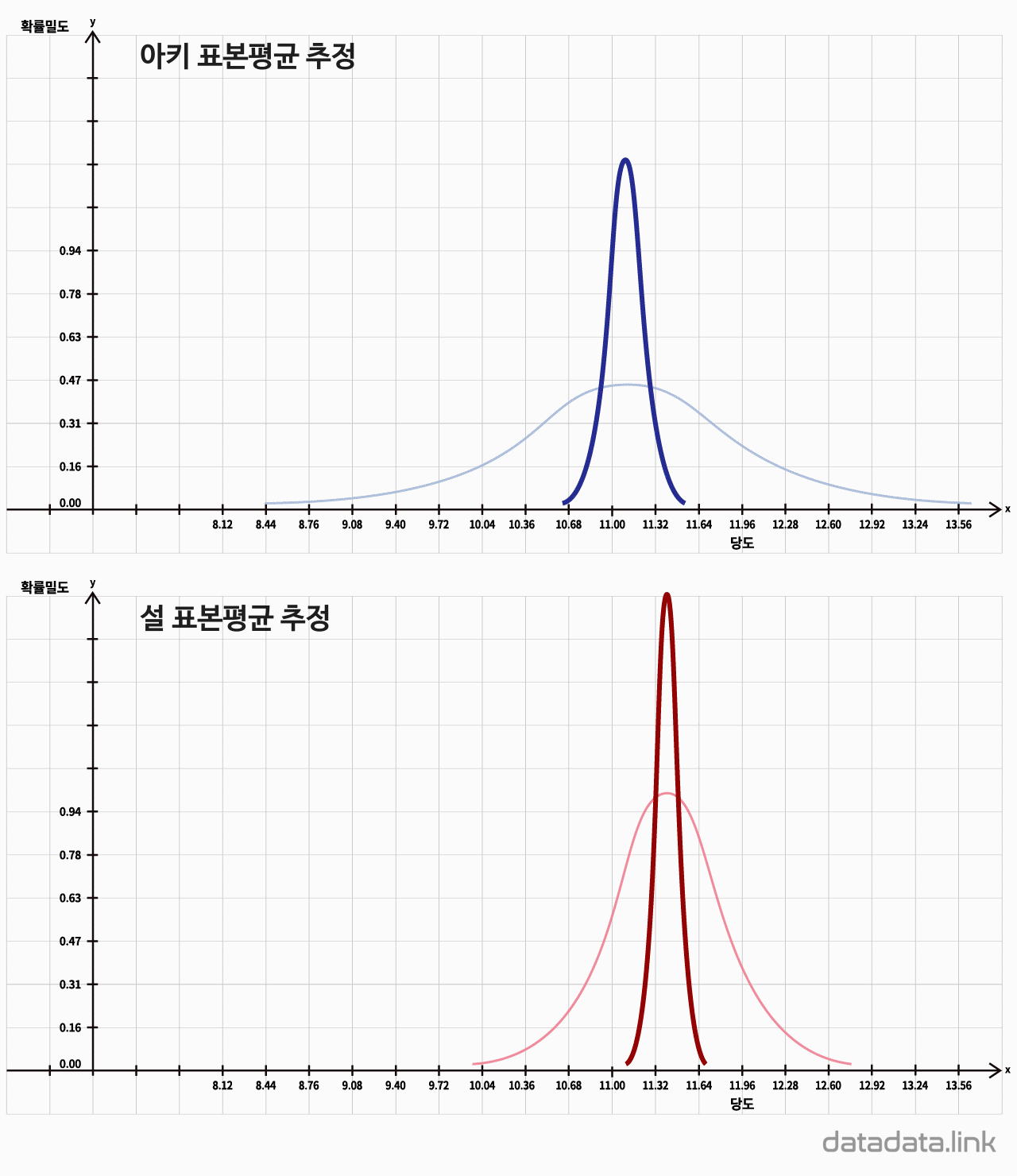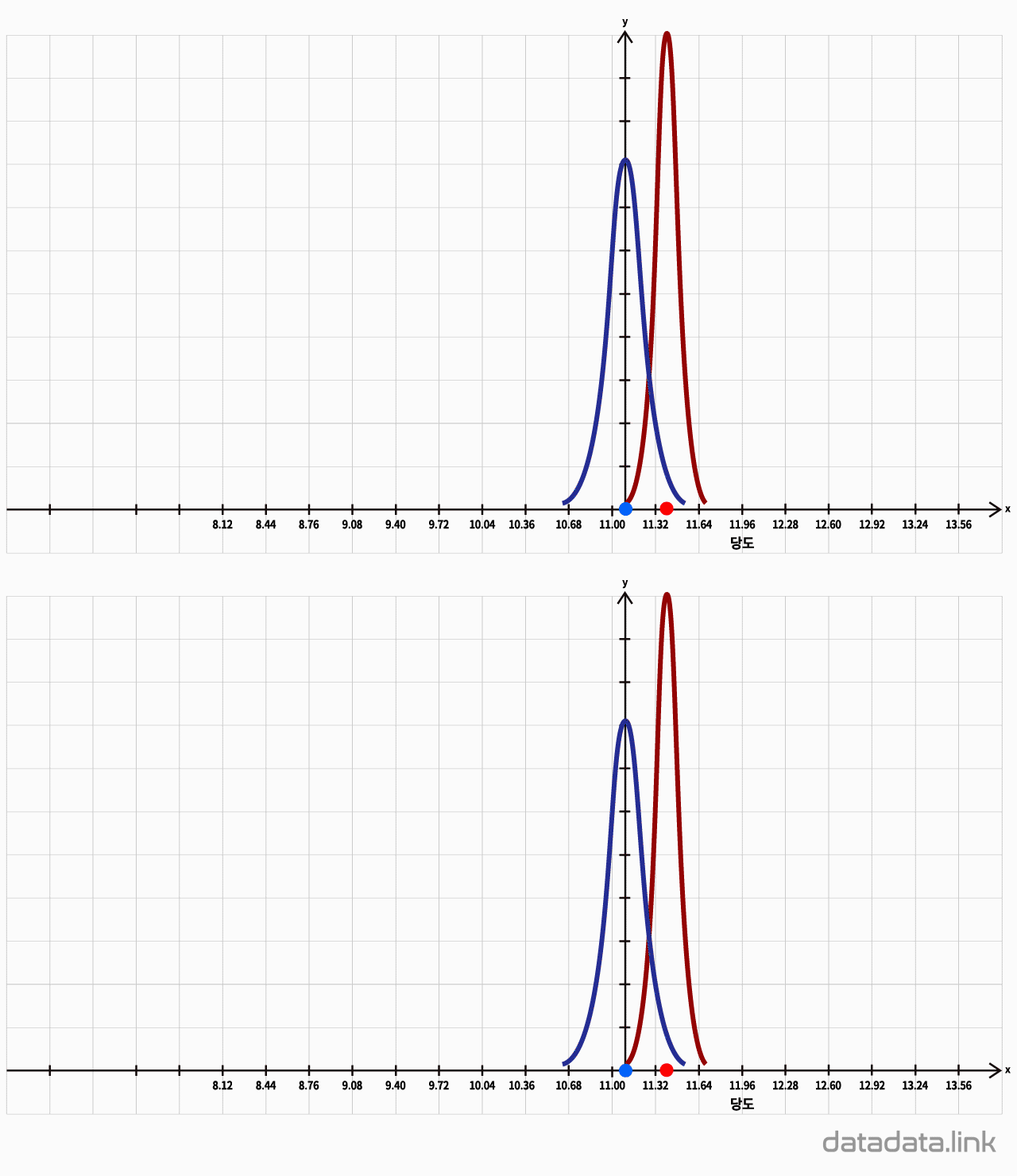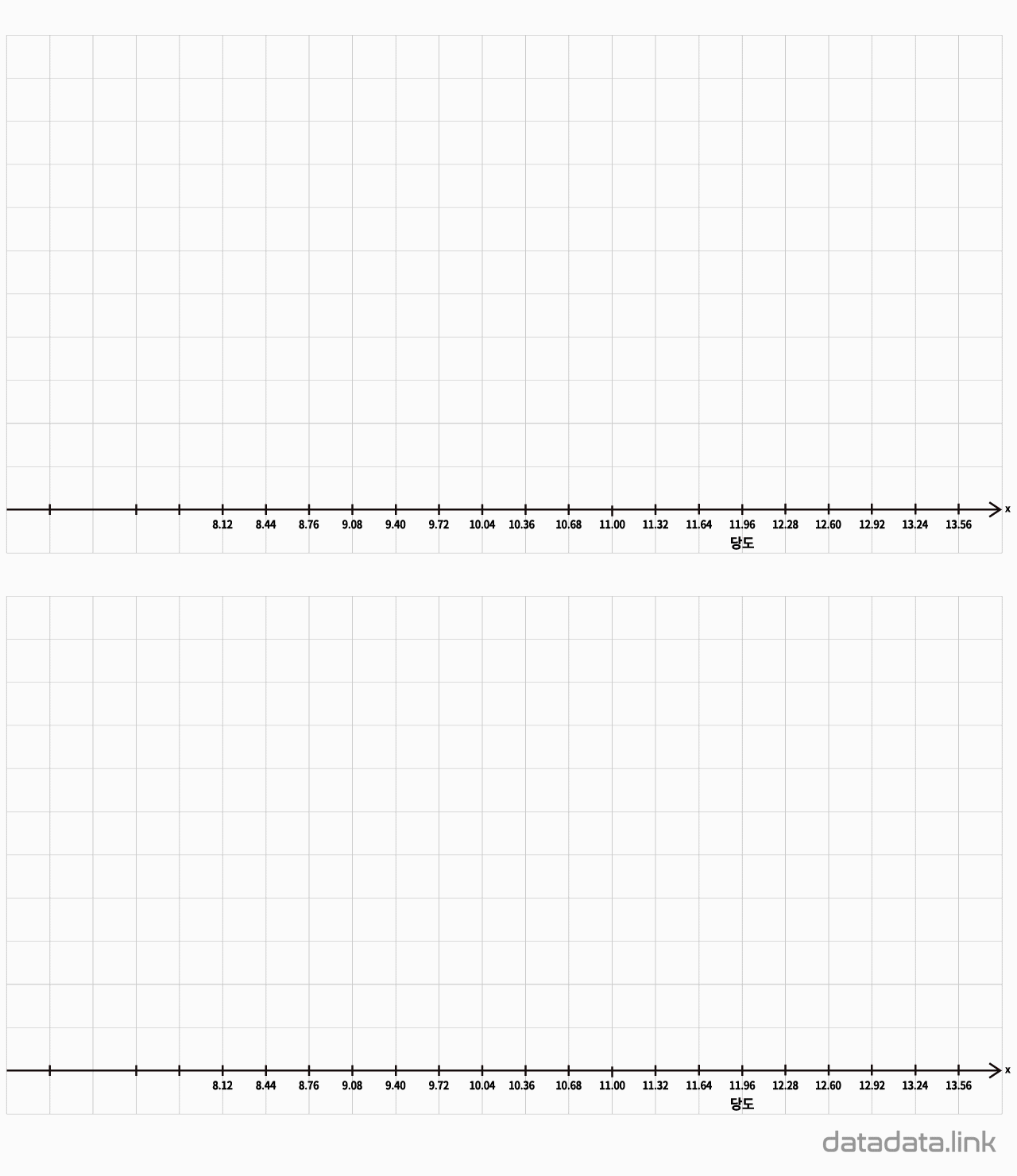
우리가 추출한 스무알의 샘플은 무한하게 추출할 수 있는 샘플들 중 하나입니다. 

샘플의 평균은 수많은 샘플의 평균들 중 하나입니다.

샘플의 평균은 샘플을 추출할 때마다 달라지게 되고, 그 샘플로부터 구한 신뢰구간도 달라지게 됩니다.

전체 설향의 당도 평균은 이 신뢰구간 내에 있을 수도 있고, 아닐 수도 있습니다.

95% 신뢰수준이란, 샘플을 랜덤하게 추출해서, 95% 신뢰구간을 구하면, 스무번 중 한 번은 전체 평균이 벗어날 수 있다는 의미입니다. 스무번 중 한 번이란 확률적으로는 5%이고, 이를 유의수준이라고 표현합니다. 

Block "2934" not found