표본분산의 표집 ?
1.1.
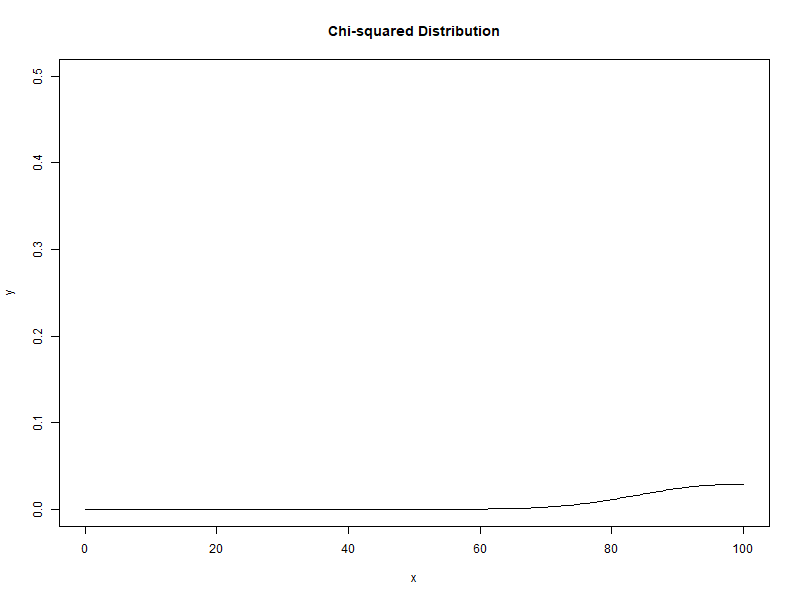
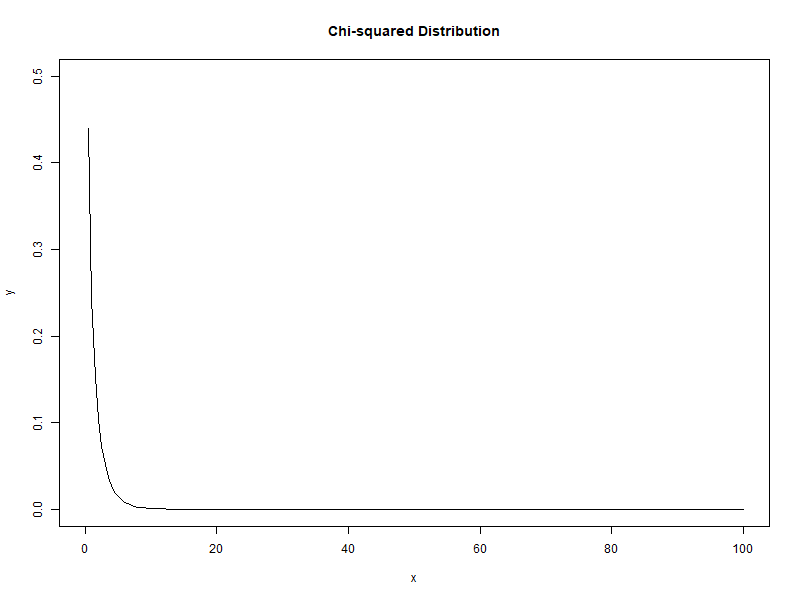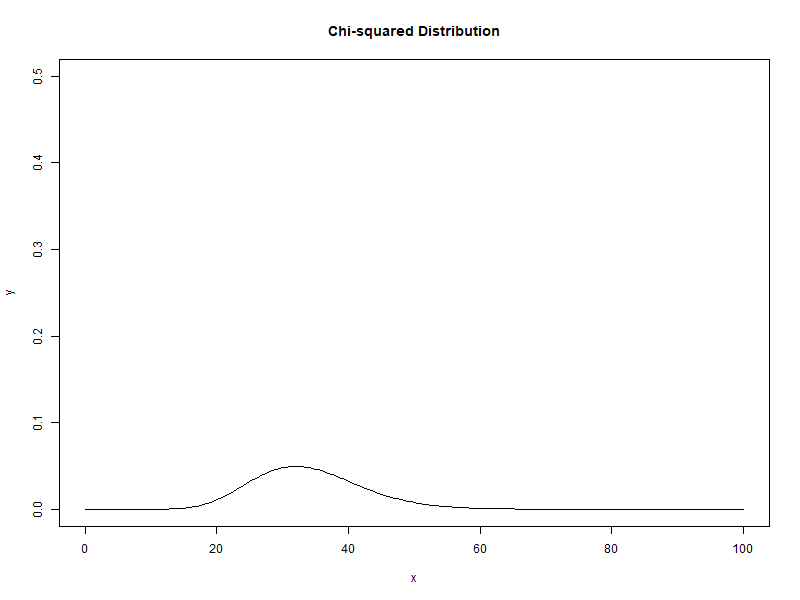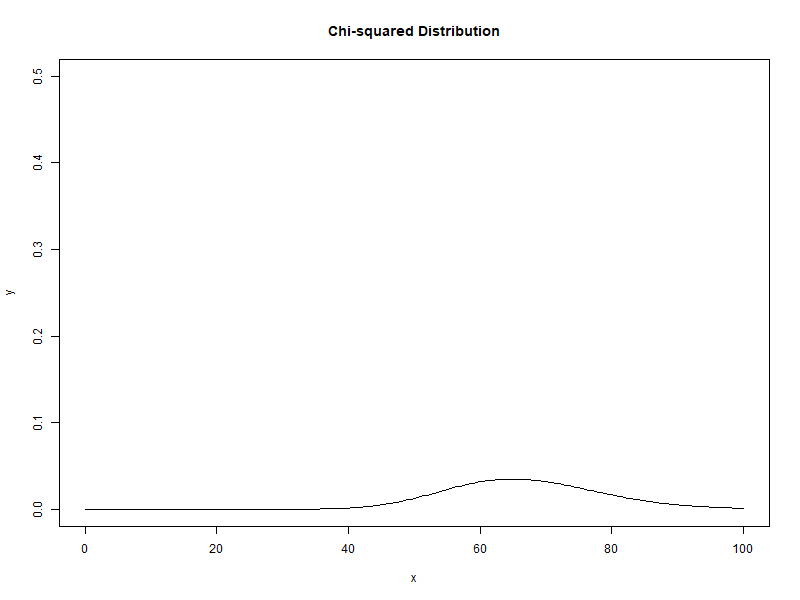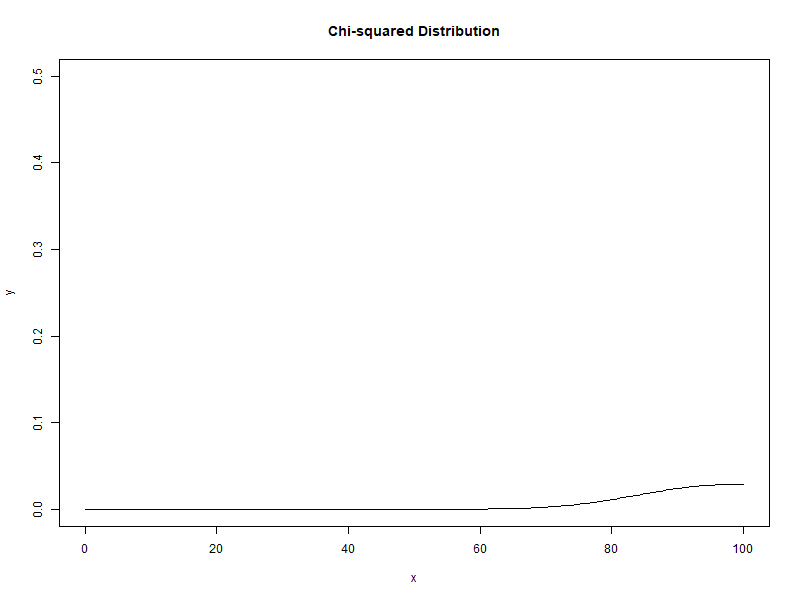
자유도가 1에서 100으로 증가할 때 카이제곱분포의 변화
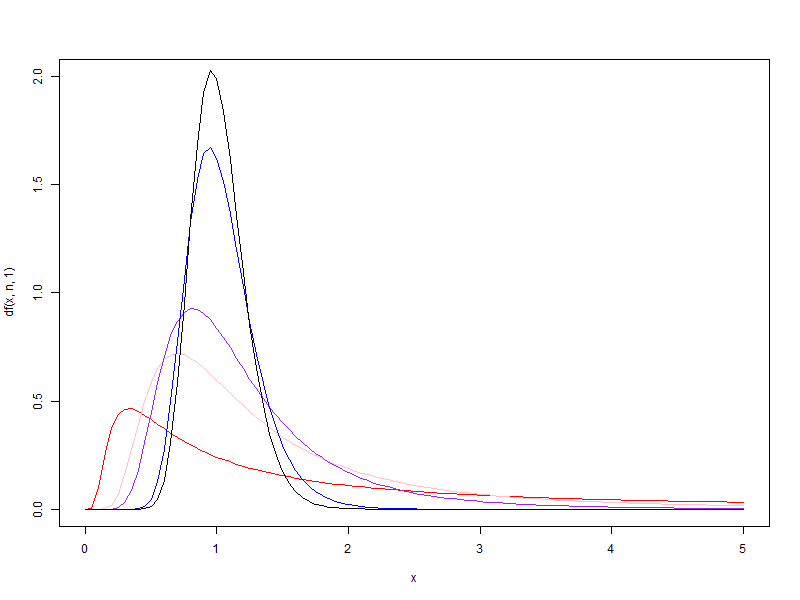
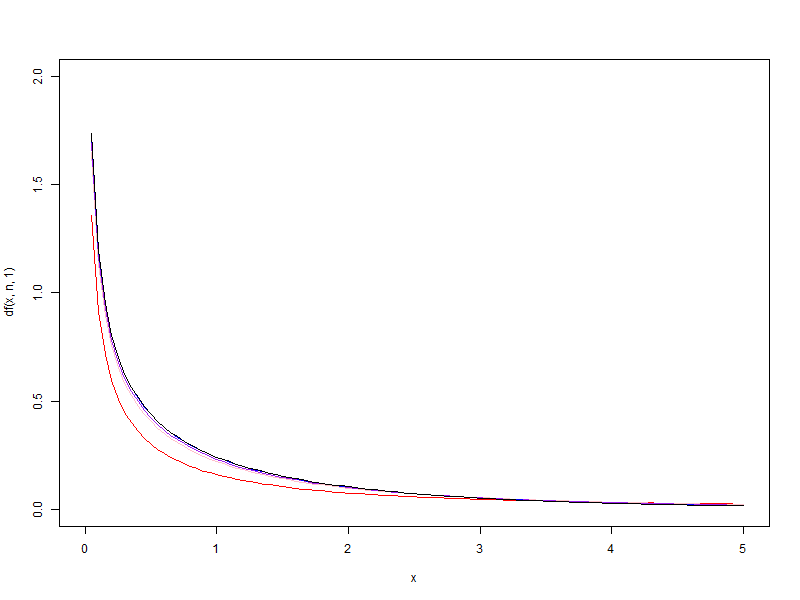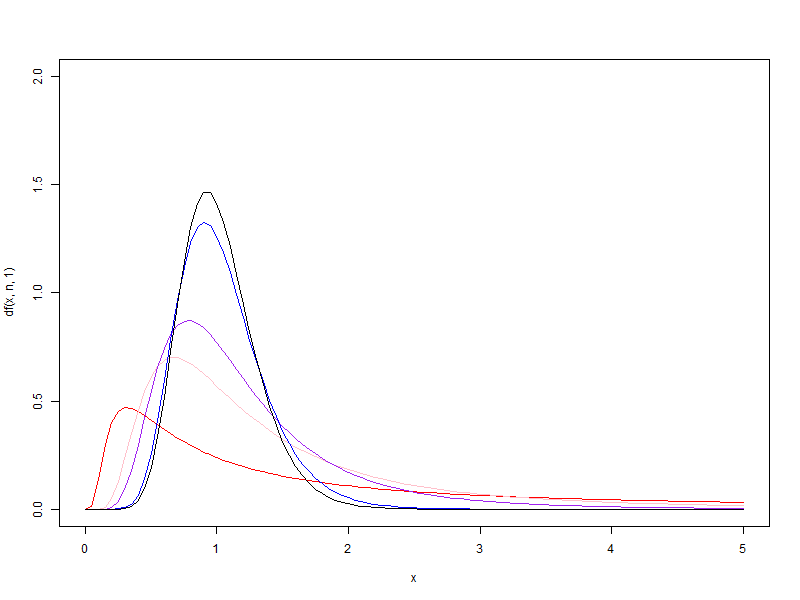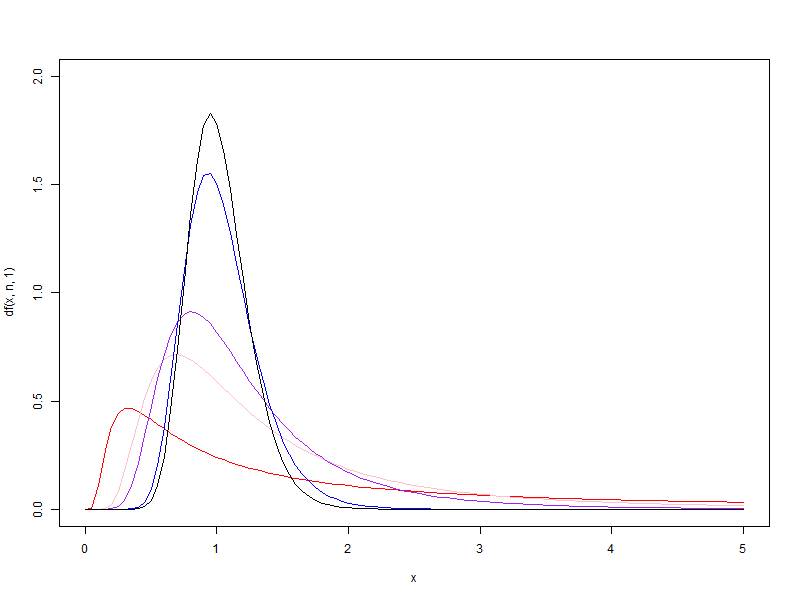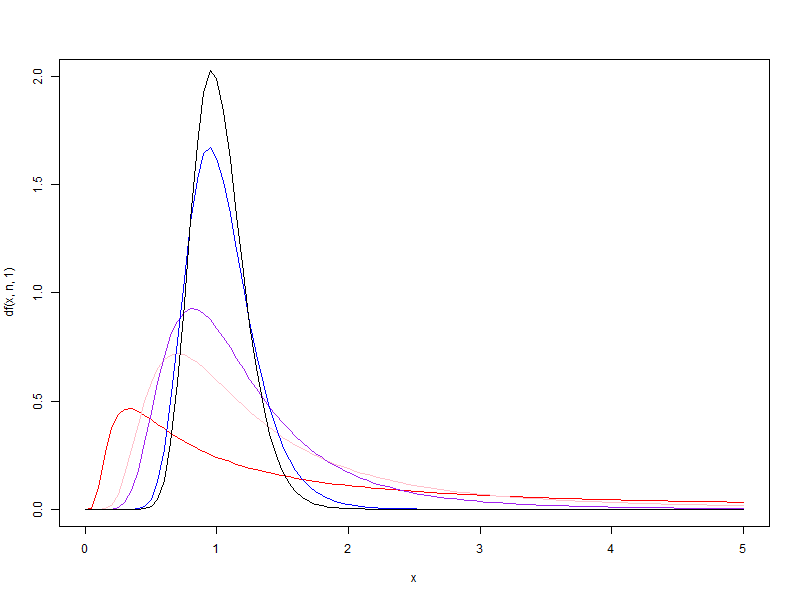
1.2. d2 가 1, 5, 10, 50, 100 일때 각각 d1 을 1에서 100으로 증가시킬 때 F분포의 변화
4.1. 용어
1. 애니메이션
2. 설명
2.1. 표본분산
확률변수가 $X$이고 집단의 모평균과 모분산이 각각 $\mu_X$, $\sigma_X^2$인 집단이 있습니다. 이 집단에서 추출한 표본의 크기가 $n$인 표본을 확률변수로 표현하면 다음과 같습니다.
{${X_1}, {X_2}, … , {X_n}$}
여기서, ${X_1}, {X_2}, … , {X_n}$은 $X$로써 같은 확률변수
표본분산($S^2$)은 표본평균($\bar X$)와 마찬가지로 확률변수입니다. 표본분산의 기준은 표본평균입니다. 따라서 표본크기가 n이라면 표본분산의 자유도는 (n-1)이 됩니다. 즉, 표본평균을 구하는데 표본크기 중 하나를 사용하여 자유도는 하나가 줄게 됩니다. 표본분산의 기대값은 집단의 모분산($\sigma^2$)입니다. 참고로, 표본평균의 기대값은 집단의 모평균($\mu$)입니다.
표본분산의 추정량(Estimator)은 다음과 같습니다.
$S_X^2=\dfrac{({X_1}-{\bar X})^2+({X_2}-{\bar X})^2+ , … , + {(X_n}-{\bar X})^2}{n-1}=\dfrac{1}{n-1}\sum\limits_{i=1}^{n}({X_i}-{\bar X})^2$
표본분산의 기대값(Expected value)은 다음과 같습니다.
${\rm E}[S^2]=\sigma^2$
참고로, 표본평균의 추정량(Estimator)은 다음과 같습니다.
${\bar X}=\dfrac{{X_1}+{X_2}+ , … , +{X_n}}{n}=\dfrac{1}{n}\sum\limits_{i=1}^{n}{X_i}$
참고로, 표본평균의 기대값(Expected value)은 다음과 같습니다.
${\rm E}[\bar X]=\mu_X$
2.2. 표본분산의 표집
집단이 정규분포를 이룬다면 표본분산의 표집은 카이제곱분포를 모분산과 자유도와 모분산의 비($\frac{n-1}{\sigma^2}$)로 표준화한 분포를 따릅니다. 표본분산의 표집의 모평균(표본분산의 기대값)은 집단의 모분산과 같고 표본분산 표집의 모분산은 다음과 같은 근사값을 가집니다.
표본분산 표집의 모평균 : 표본분산 기대값
${\rm E}[S_{X}^2]=\mu_{S_{X}^2}∼\sigma_X^2$
표본분산 표집의 모분산
${\rm Var}(S_{X}^2)=\sigma_{S_{X}^2}^2∼\dfrac{2\sigma_X^4}{n-1}$
여기서, $n$은 표본크기
표본분산 표집의 모표준편차
${\rm SD}(S_{X}^2)=\sigma_{S_{X}^2}∼\sqrt{\dfrac{2\sigma_X^4}{n-1}}$
참고로, 집단이 정규분포를 이룬다면 표본평균의 표집은 정규분포를 이룹니다, 표본평균 표집의 모평균(표본평균의 기대값)은 집단의 모평균과 같고 표본평균 표집의 모분산은 집단의 모분산을 표본의 자유도로 나눈 값과 같습니다.
2.3. 확률변수인 표본분산을 무차원 확률변수인 카이제곱으로 변환 후 카이제곱분포를 표본분산의 표집분포 분석에 사용
표본분산을 무차원 확률변수인 카이제곱으로 변환하면 다음과 같습니다.
$\chi_{n-1}^2=(n-1)\dfrac{S^2}{\sigma^2}$
위식의 카이제곱분포의 모수인 자유도(degree of freedom, $df$)는 다음과 같습니다.
$df = n-1$
표본의 크기가 n인 표본의 분포값을 표본분산(variance) $\rm S^2$이라고 합니다. 표본평균과 마찬가지로 표본분산($\rm S^2$)도 확률변수이며 따라서 확률분포인 표집분포(sampling distribution of sample variances)를 가집니다. 표본분산과 모집단의 관계를 알 수 있다면 표본에서 구할 수 있는 표본분산으로 모집단의 모분산을 추정할 수 있습니다.
표본분산의 확률분포를 표본분산의 표집분포(sampling distribution of sample variances)라 합니다. 확률변수인 표본분산은 음수일 수도 있는 표본평균과 달리 음수가 아닌 0과 양의 실수입니다. 그리고 표본분산은 큰 값을 갖는 확률보다는 0에 가까운 작은 값을 갖는 확률이 더 큰 비대칭분포를 보입니다. 그리고 표본분산($\rm S^2$)을 모분산으로 나누어서 표준화를 하고 표본의 자유도(n-1)를 곱한 값을 카이제곱($\chi_{n-1}^{2}$)이라하고 아래식처럼 표현할 수 있습니다.
$\chi_{n-1}^{2}=\left({n-1}\right){\dfrac{S^{2}}{\sigma^{2}}}$
새로운 확률변수인 카이제곱($\chi_{n-1}^{2}$)은 카이제곱분포(chi-squared distribution)를 나타냅니다. 카이제곱분포는 자유도(degree of freedom)이라는 모수(parameter)를 가지며, t분포와 마찬가지로 자유도마다 확률분포가 있으며, 따라서 무수히 많은 확률분포를 가집니다.
정리하면, 집단이 $\sigma^2$인 정규분포를 나타내고 표본의 크기가 n인 표본을 단순임의복원추출하면, 확률변수인 표본분산($\rm S^2$)을 집단의 모분산($\sigma^2$)으로 표준화하고 자유도(n-1)를 곱한 새로운 확률변수인 카이제곱( $\chi^2$)은 자유도에 따른 카이제곱분포를 따릅니다.
3. 실습
3.2. 구글시트 함수
=FACT(A3) : 숫자의 계승. A3에 있는 숫자의 계승을 계산함. 예를 들어, A3에 있는 숫자가 2이면, 2×1(2곱하기 1)의 값을 계산해서 표시함. A3에 있는 숫자가 3이면, 3×2×1(3곱하기2곱하기 1)의 값을 계산해서 표시함.
=POWER(C3,B3) : 거듭제곱. C3의 값을 B3의 값만큼 거듭제곱한 값을 계산해서 표시함.
=SQRT(D3) : 제곱근. D3에 있는 값의 제곱근을 계산해서 표시함.
=COUNTIF(J3:J10,L3) : 범위에서 조건에 맞는 개수. J3에서 J10에서 L3의 값을 가진 데이터의 개수를 표시함. $표시를 알파벳 앞뒤로 넣으면, 셀을 복사해도 그 값이 바뀌지 않음.
=AVERAGE(R3:S3) : 평균. R3에서 S3에 있는 데이터의 평균을 계산해서 표시함.
=VARP(R3:S3) : 모분산. R3에서 S3에 있는 데이터의 모분산을 계산해서 표시함. 편차제곱합을 데이터의 개수로 나눠서 구함.
=VAR.S(R3:S3) : 표본분산. R3에서 S3에 있는 데이터의 표본분산을 계산해서 표시함. 편차제곱합을 (데이터의 개수-1)로 나눠서 구함.
=SUM(AF3:AF9) : 합계. AF3에서 AF9에 있는 데이터의 합계.
3.3. 실습강의
이항분포
이항분포에서 실현된 집단
집단으로부터 가능한 모든 표본
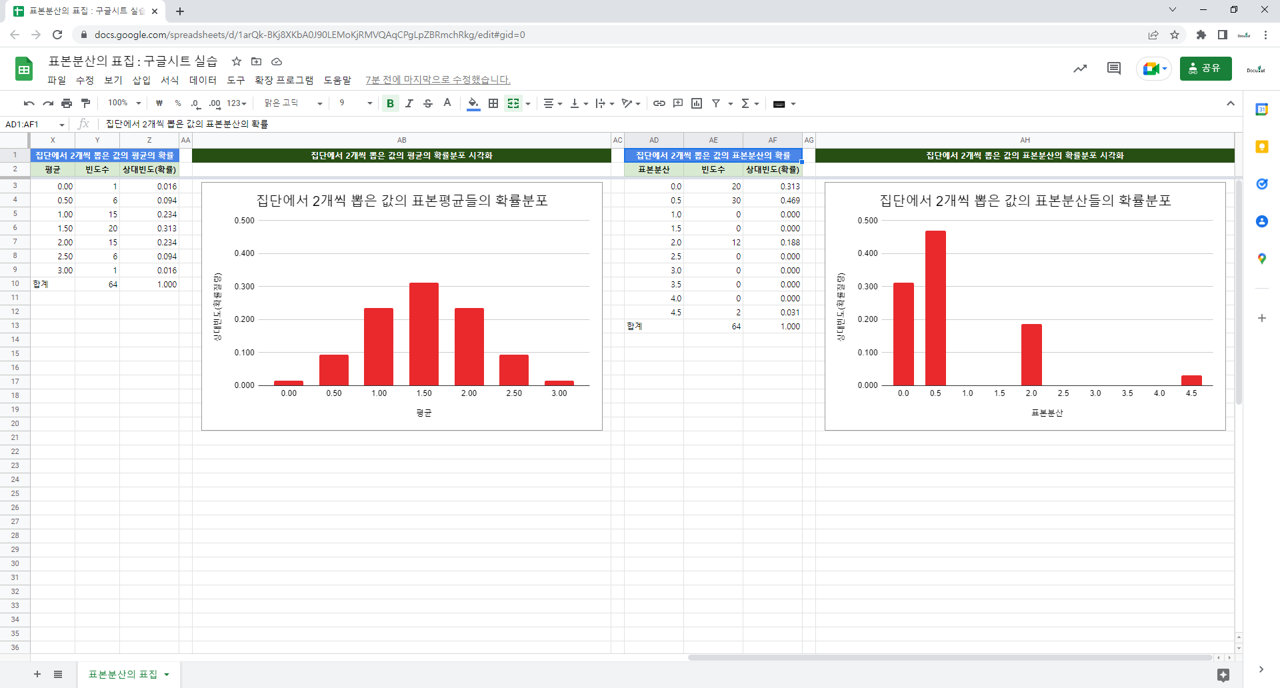
표본분산
표본분산의 표집
4. 용어와 수식
4.1 용어