표본비율의 표집 ?
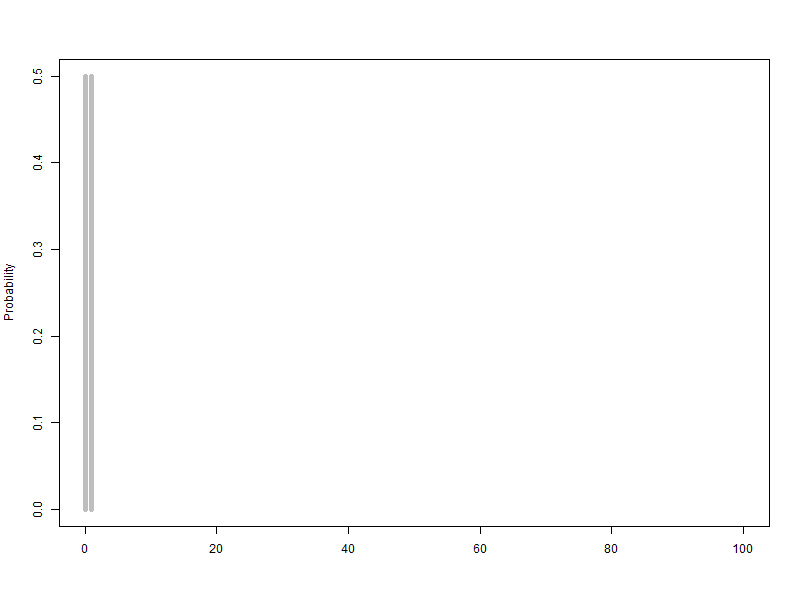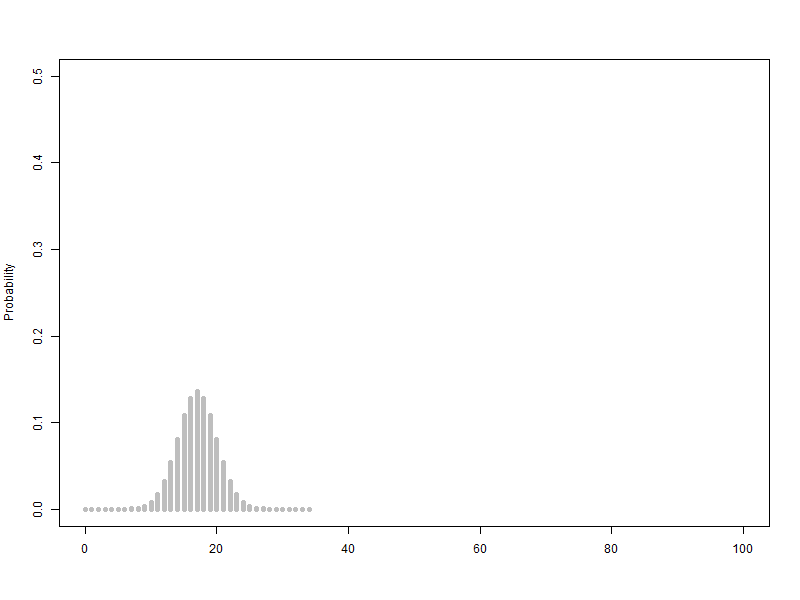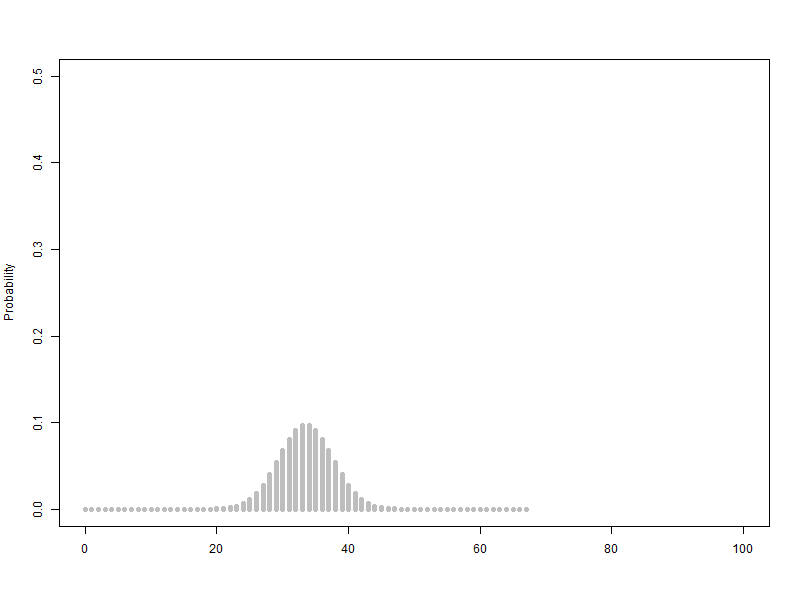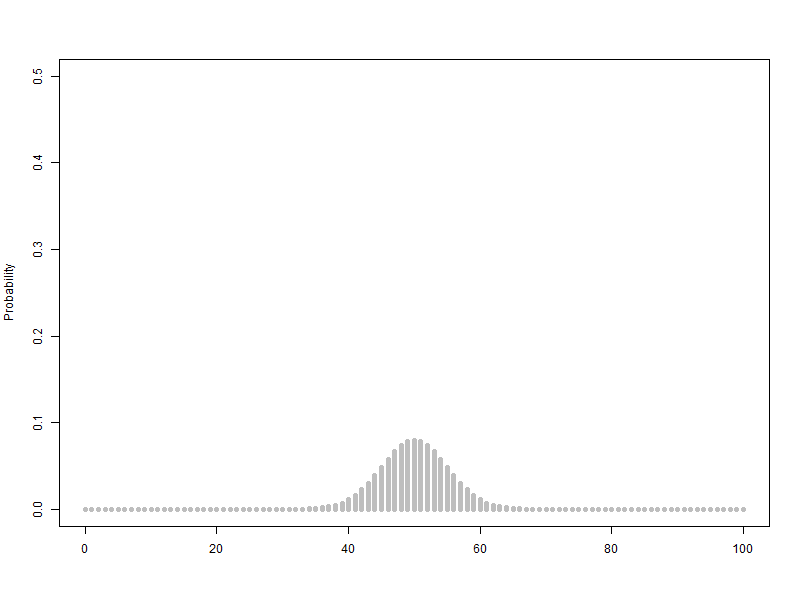
1.1. 베르누이 확률변수를 2개에서 100개까지 늘리는 이항분포(p=0.5) 애니메이션
4.1. 용어
1. 애니메이션
2. 설명
2.1. 표본비율(Sample Proportion)
표본을 나타내면
${\textstyle \{x_{1},\ldots ,x_{n}\}}$
표본을 베르누이 시행의 결과라고 생각하면 다음과 같이 표현할 수 있습니다.
$$x \sim B(성공,실패;n,{\hat p})$$
여기서, 확률변수 $x$는 성공과 실패 두가지 값을 가짐
$n$은 표본크기
베르누이 시행의 확률분포를 나타내 보면 다음과 같습니다.
$$\mathrm{P}(x=성공)=\hat p$$
$$\mathrm{P}(x=실패)=1-\hat p$$
표본비율의 추정량(Estimator)은 다음과 같습니다.
$$\hat p= \dfrac {X}{n}$$
여기서, $\hat p$는 표본비율
$X$는 베르누이 시행에서 성공횟수 ; 성공을 값으로 가지는 표본원소의 수
$n$은 표본크기
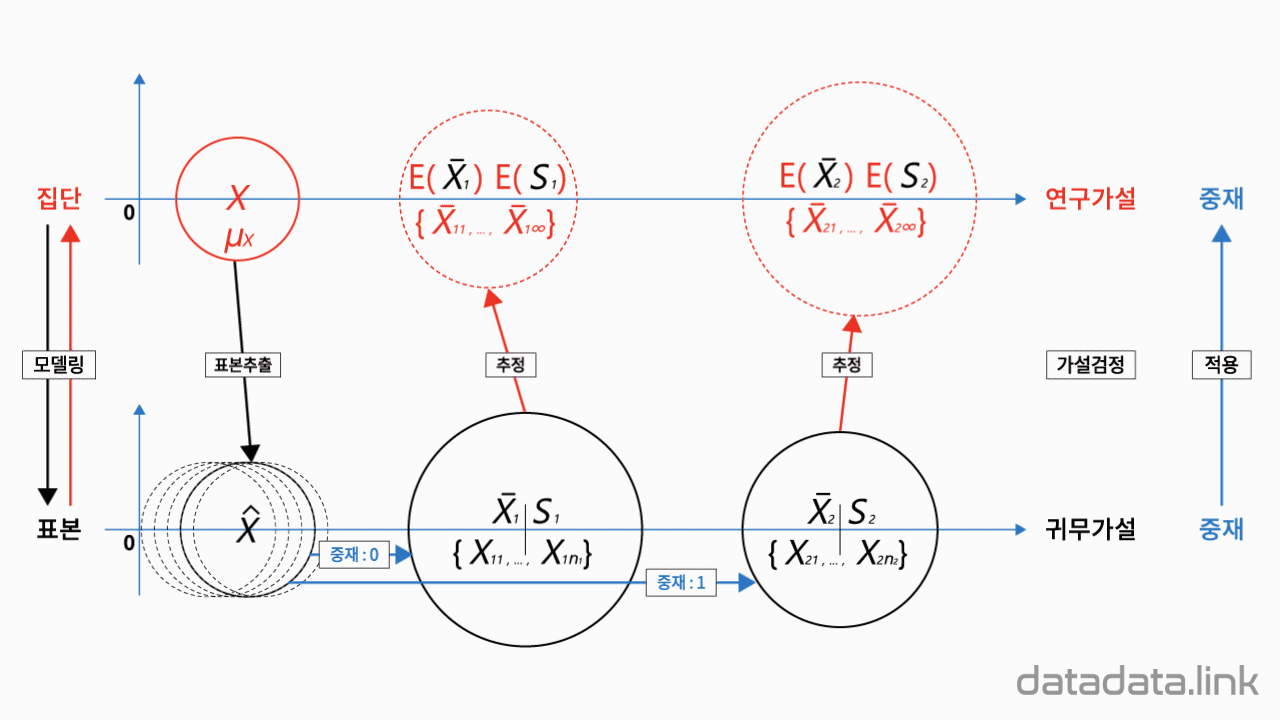
표본비율($\hat{p}$)은 모비율($p$)의 비편향, 효율, 일치 추정량입니다. 표본비율($\hat{p}$)은 모비율($p$) 추정시 좋은 추정량의 조건을 모두 가지고 있습니다. 그래서, 모비율의 점추정에는 표본비율을 사용합니다. 베르누이 시행에서의 성공확률을 표본비율이라고 할 수 있습니다. 표본비율 표집의 모평균(표본비율의 기대값)과 표본비율 표집의 모분산은 다음과 같습니다.
$${\rm E}(\hat p)=p$$
$${\rm Var}(\hat p)={\rm Var}(\dfrac{X}{n})=\dfrac{1}{n^2}{\rm Var}(X)=\dfrac{1}{n^2}np(1-p)=\dfrac{p(1-p)}{n}$$
여기서, $X$는 베르누이 시행에서 성공횟수
$n$은 표본크기
$\dfrac{X}{n}$은 표본비율($p$)
표본비율의 표준오차는 표본비율 표집의 모표준편차와 같으며 다음과 같이 정의합니다.
$${\rm SE}(\hat p)=\sigma_{\hat p}=\dfrac{\sigma_p}{\sqrt n}=\dfrac{\sqrt{p(1-p)}}{\sqrt n}=\sqrt{\dfrac{p(1-p)}{n}}$$
모비율($p$)은 일반적으로 모르는 경우가 많은 미지수이므로 $\hat{p}$로 대치하여 표준오차의 추정량을 구합니다. $\hat{p}$의 표준오차(Standard Error) 추정량은 다음과 같습니다.
$${\rm SE}(\hat p) \sim \sqrt{\dfrac{{\hat p}(1-{\hat p})}{n}}=\dfrac{1}{n}\sqrt{\dfrac{X(n-X)}{n}}$$
여기서, $X$는 베르누이 시행에서 성공횟수
$n$은 표본크기
$n-X$는 베르누이 시행에서 실패횟수
표본비율($p$)은 $\dfrac{X}{n}$
표준오차의 추정량은 t분포를 이용한 구간추정에 사용할 수 있습니다.
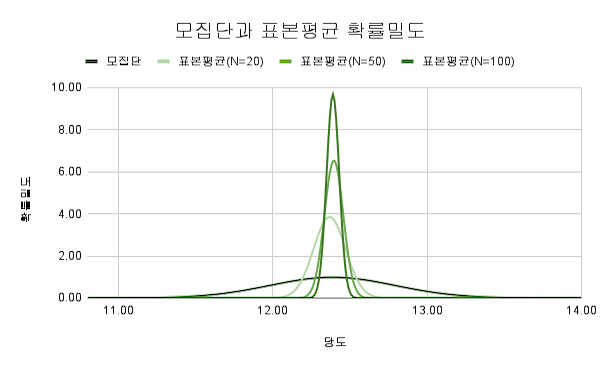
2.2. 표본비율($\hat p$) 표집
표본비율($\hat p$) 표집의 확률밀도함수는 다음과 같습니다.
$${N}\left({p,\dfrac{{p}{(}{1}{-}{p}{)}}{n}}\right)$$
여기서, $p$는 집단의 모비율
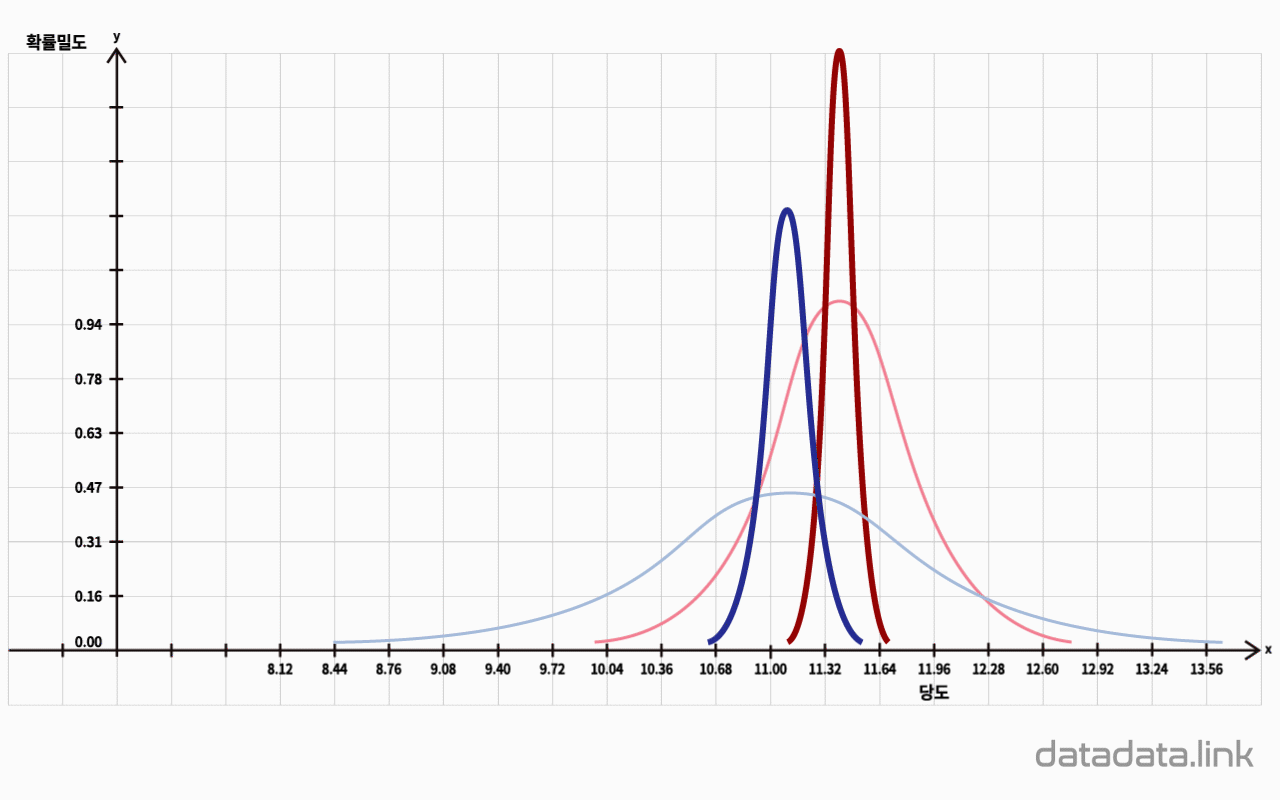
표본크기가 충분히 클 때 표본비율($\hat{p}$)의 확률밀도함수는 평균이 $\hat{p}$, 분산이 $\dfrac{{\hat p}(1-{\hat p})}{n}$인 정규분포에 근사합니다.
$${\hat p}\sim N\left({\hat p},\dfrac{{\hat p}(1-{\hat p})}{n}\right)$$
여기서, $0 < {\hat p} < 1$
한편, 유한개($N$)의 원소를 가지는 유한집단에서 비복원추출하는 경우에는 표본비율($\hat{p}$) 표집의 모분산에 수정항인 $(N-n)/(N-1)$을 곱하여 보정합니다. 신뢰구간을 추정할 때 표본크기($n$)가 충분히 크다고 할 수 있는 기준은 다음과 같습니다.
${n}\hat{p}{>}{5}{,}\hspace{0.33em}{n}\left({{1}{-}\hat{p}}\right){>}{5}$
표본크기가 충분히 크면 표본비율 ($\hat{p}$)의 분포는 정규분포에 근사하게 된다는 사실로부터 모비율($p$)의 구간추정은 다음과 같이 할 수 있습니다.
모비율($p$)의 $100(1-\alpha)%$ 신뢰구간 – 크기가 큰 표본인 경우
$\left[{\hat{p}{-}{z}_{\mathit{\alpha}{/}{2}}\sqrt{\dfrac{\hat{p}\left({{1}{-}\hat{p}}\right)}{n}}{,}\hspace{0.5em}{\hat{p}{+}{z}_{\mathit{\alpha}{/}{2}}\sqrt{\dfrac{\hat{p}\left({{1}{-}\hat{p}}\right)}{n}}}}\right]$
표본크기가 작은 경우에는 비모수 검정을 행합니다.
3. 실습
3.2. 구글시트 함수
=FACT(A3) : 숫자의 계승. A3에 있는 숫자의 계승을 계산함. 예를 들어, A3에 있는 숫자가 2이면, 2×1(2곱하기 1)의 값을 계산해서 표시함. A3에 있는 숫자가 3이면, 3×2×1(3곱하기2곱하기 1)의 값을 계산해서 표시함.
=POWER(C3,B3) : 거듭제곱. C3의 값을 B3의 값만큼 거듭제곱한 값을 계산해서 표시함.
=COUNTIF(J3:J10,L3) : 범위에서 조건에 맞는 개수. J3에서 J10에서 L3의 값을 가진 데이터의 개수를 표시함. $표시를 알파벳 앞뒤로 넣으면, 셀을 복사해도 그 값이 바뀌지 않음.
=COUNT(R3:S3) : 데이터개수, R3에서 S3에 있는 수치화된 데이터의 개수.
=AVERAGE(R3:S3) : 평균. R3에서 S3에 있는 데이터의 평균을 계산해서 표시함.
=VARP(R3:S3) : 모분산. R3에서 S3에 있는 데이터의 모분산을 계산해서 표시함. 편차제곱합을 데이터의 개수로 나눠서 구함.
=SUM(AF3:AF9) : 합계. AF3에서 AF9에 있는 데이터의 합계.
3.3. 실습강의
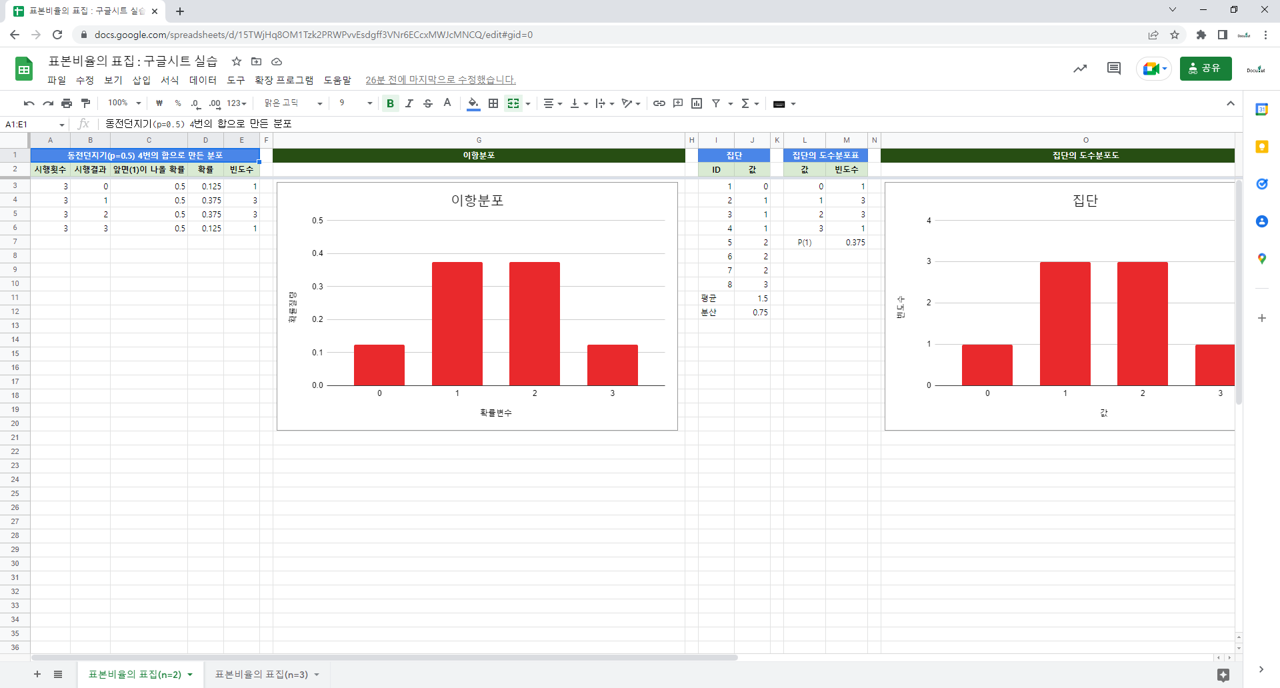
이항분포
이항분포에서 실현된 집단
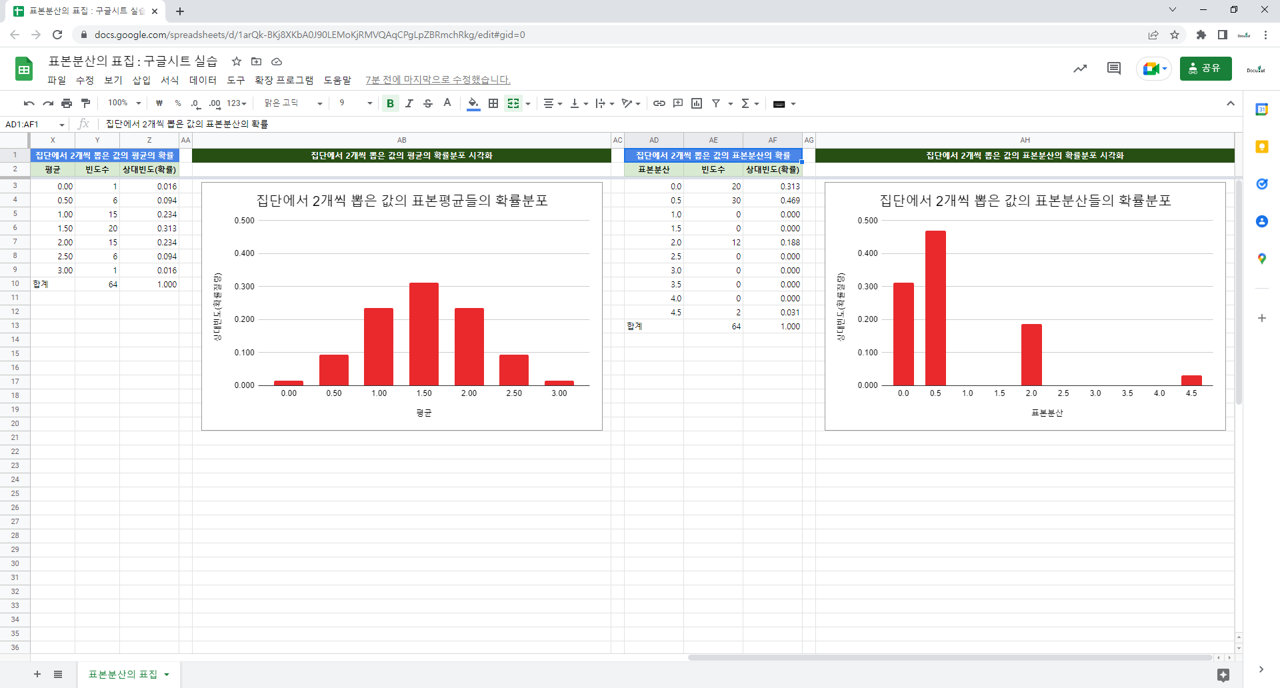
집단으로부터 가능한 모든 표본
표본비율
표본비율의 표집
4. 용어와 수식
4.1 용어