표본크기 결정 ?
1. 애니메이션
2. 설명
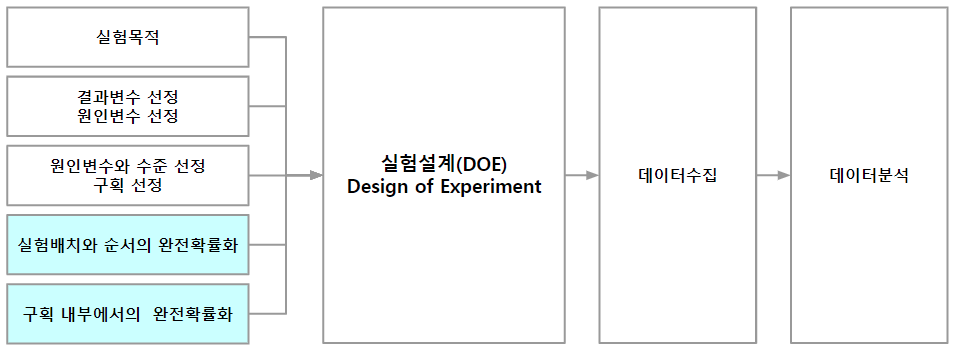
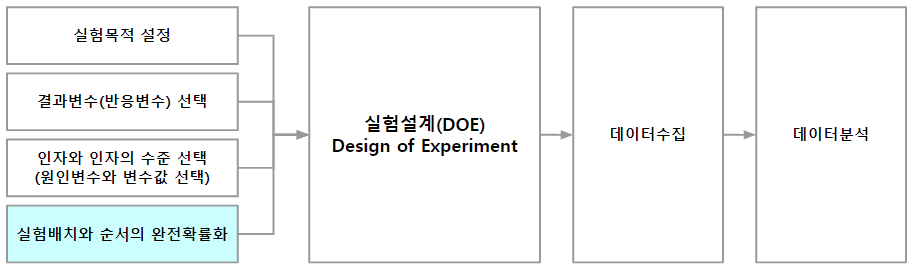
실험설계에서는 표본을 추출하기 전에 표본크기를 얼마로 할 것인가를 정해야 합니다. 표본크기를 크게 할수록 표준오차는 작아지고 추정의 정밀도는 더욱 높아집니다. 일반적으로 표본크기가 클수록 모수를 구간추정할 때 같은 유의수준이라도 신뢰구간이 커집니다. 표본크기를 늘리는 것은 실험의 비용을 늘리기 때문에 먼저 추정의 유의수준과 신뢰구간을 미리 설정하여 표본크기의 방정식을 만들어 최소한의 표본의 크기를 결정합니다.
모평균 추정시 표본크기 결정
모평균의 $100(1-\alpha)$% 신뢰구간은 다음과 같습니다.
$\left[\bar{X}-z_{\frac{\alpha}{2}}\dfrac{{\sigma_X}}{\sqrt{n}},\bar{X}+z_{\frac{\alpha}{2}}\dfrac{{\sigma_X}}{\sqrt{n}}\right]$
여기서, $\mu_X$은 모평균
$\sigma_X$은 모표준편차
${z}_{\frac{\alpha}{2}}\dfrac{\mathit{\sigma}}{\sqrt{n}}$ 를 오차의 한계(bound on the error of estimation)또는 최대허용오차(maximum allowable error)라고 합니다. 오차의 한계를 $d$로 하기 위한 표본크기는 다음 방정식을 $n$에 관하여 풀면 됩니다.
${z}_{\frac{\alpha}{2}}\dfrac{\mathit{\sigma}}{\sqrt{n}}=d$
모평균 추정시 표본크기의 결정
$n=\left(\dfrac{z_{\frac{\alpha}{2}}\sigma_X}{d}\right)^2$
위 식에서 모표준편차 $\sigma_X$는 알 수가 없으므로 $X$의 범위를 추정하고 4로 나눈 값을 사용합니다.
모비율 추정시 표본크기 결정
비슷한 방법으로 모비율 $p$의 100(1-$\alpha$)% 신뢰구간은 다음과 같습니다.
$\left[{\hat{p}{-}{z}_{\frac{\alpha}{2}}\sqrt{\dfrac{\hat{p}{(}{1}{-}\hat{p}{)}}{n}}{,}\hspace{0.33em}\hat{p}{+}{z}_{\frac{\alpha}{2}}\sqrt{\dfrac{\hat{p}{(}{1}{-}\hat{p}{)}}{n}}}\right]$
따라서 오차한계가 $d$가 되기 위해 아래의 방정식을 표본크기($n$)에 대하여 풉니다.
${z}_{\frac{\alpha}{2}}\sqrt{\dfrac{\hat{p}{(}{1}{-}\hat{p}{)}}{n}}{=}{d}$
모비율 추정시 표본의 크기 결정
${n}{=}\hat{p}{(}{1}{-}\hat{p}{)(}\dfrac{{z}_{\frac{\alpha}{2}}}{d}{)}^{2}$
위 식에서 $\hat{p}$는 구하기 전이고 모비율은 알 수 가 없으므로 $\hat{p}$를 보통 0.5로 합니다. 그 이유는 $p=0.5$일 때 자연현상에서 가장 흔한 대칭이기 때문입니다.
3. 실습
3.2. 구글시트 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
=RANDBETWEEN(1,100) : 두 값 사이(두 값 포함)의 고르게 분산된 정수인 난수를 반환.
=INDIRECT(D3&”:”&E3) : 문자열로 지정된 셀 참조를 반환.
=COUNTIF(F2:F2, ROW(D3:E3)) : 범위에서 조건에 맞는 개수를 표시.
=NOT(논리표현식) : 논리 값의 역을 반환.
=LARGE(데이터집합, n) : 데이터 집합에서 n번째로 큰 요소를 반환.
=ARRAYFORMULA : 배열 수식에서 여러 행 또는 열에 반환된 값을 표시.
=ARRAY_CONSTRAIN : 배열 결과를 지정된 크기로 제한.
=VLOOKUP(H3,A:B,2,FALSE) : 열 방향 검색. A:B열의 첫 번째 열에서 H3값이 있는 행의 2번째 값을 표시합니다. FALSE를 입력하면, 완전히 일치된 값만 표시합니다. FALSE가 아닌 TRUE를 입력하면, H3에 근접한 값(H3보다 작거나 같은 값)이 있는 행의 2번째 값을 표시합니다.
=AVERAGE(B3:B1002) : 평균. B3에서 B1002에 있는 데이터의 평균.
=VARP(B3:B1002) : 모분산. B3에서 B1002에 있는 데이터의 모분산. 편차제곱합을 데이터 개수로 나눔.
=STDEV.P(B3:B1002) : 모표준편차. B3에서 B1002에 있는 데이터의 모표준편차. 모분산의 제곱근.
=COUNT(I3:I22) : 데이터 개수. I3에서 I22에 있는 숫자로 표시된 데이터의 개수.
=VAR.S(I3:I22) : 표본분산. I3에서 I22에 있는 데이터의 표본분산. 편차제곱합을 데이터 개수 -1로 나눔.
=STDEV.S(I3:I22) : 표본표준편차. I3에서 I22에 있는 데이터의 표본표준편차. 표본분산의 제곱근.
=AK3/SQRT(AH3) : AK3 값을 AH3의 제곱근으로 나눔. 이 실습에서는 표준오차를 계산함.
=T.INV(1-(1-AN3)/2,AH3-1) : T확률분포에서 T값을 계산. T.INV(확률, 자유도)로 구성. 이 실습에서는 AN3에 95% 신뢰수준을 입력하였는데, 양측검정에서는 양쪽 끝 확률이 각각 2.5%가 되어야 함. 따라서, 1-(1-0.95)/2를 하면 누적확률밀도가 0.975, 즉 97.5%가 되어서, 양쪽 끝 확률이 각각 2.5%인 T값을 얻을 수 있음.
=AND(AR3>AP3, AR3<AQ3) : 입력된 조건이 모두 참이면 TRUE, 입력된 조건 중 하나라도 거짓이면, FALSE를 표시. AR3값이 AP3 초과이고, AQ3 미만이면 TRUE를 표시함.
=NORMSINV(1–(1–AP3)/2) : 표준정규분포의 역함수. 괄호안의 값을 누적확률로 가지는 표준정규분포 상의 확률변수를 구함. 이 실습에서는 AP3에 0.95, 즉 95% 신뢰구간 값을 넣었는데, 좌우대칭의 양 끝 확률이 0.25 (2.5%)가 되도록 하기 위해, 1–(1–AP3)/2=0.975 (97.5%)로 계산해서 입력함.
3.3. 실습강의
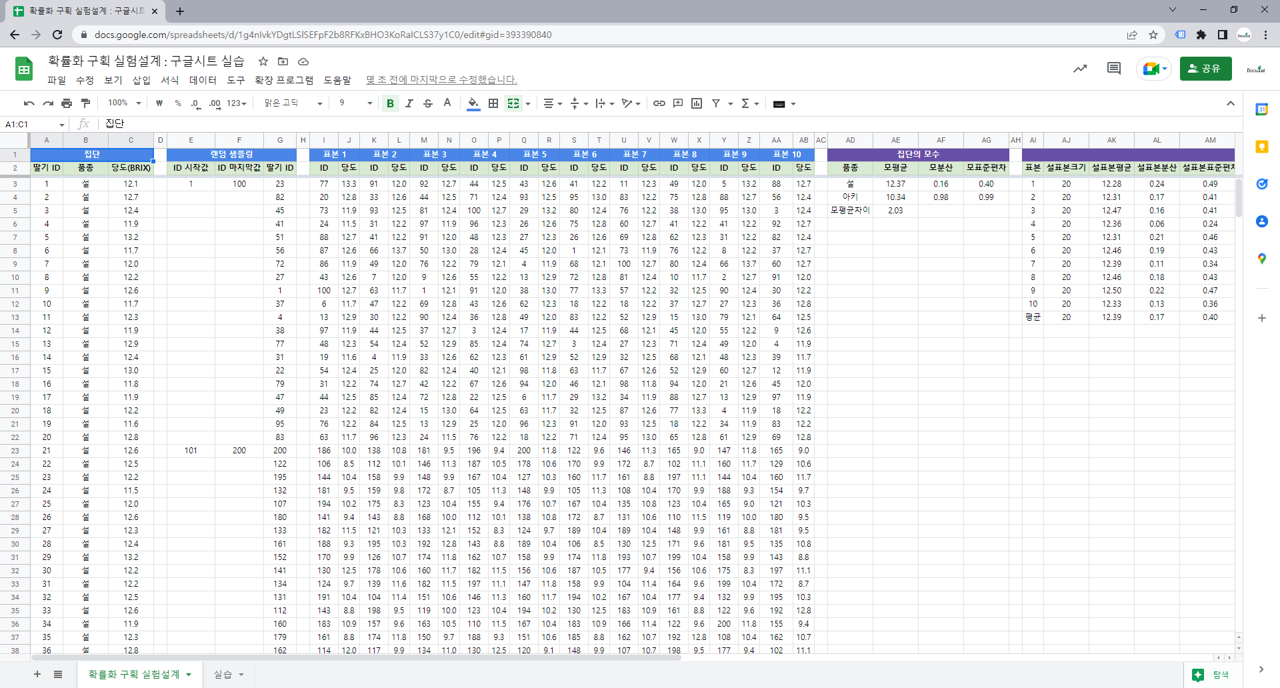
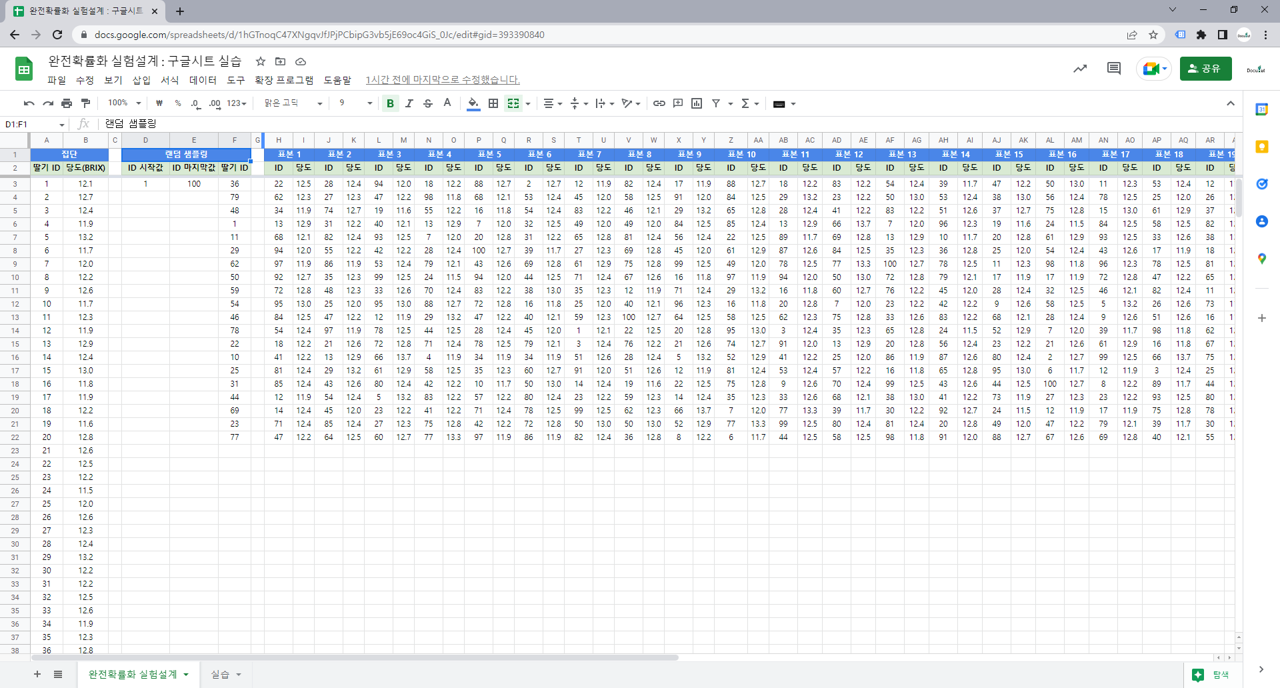
– 집단
– 랜덤 샘플링 : 무작위로 표본추출
– 표본통계량
– 표본통계량으로 모수 추정(점, 구간)
– 표본크기에 따른 표준오차 비교
– 표본크기 결정
– 실습 안내