2차원 좌표계 ?
2D coordinate system ?
1.1. 2차원 직교좌표계
1. 애니메이션
2. 설명
2.1. 2차원 좌표계
두 변수를 가지는 개체(요소, 객체, object, element)를 시각화 할 때, 2차원 좌표계를 사용할 수 있습니다. 2차원 좌표계에는 대표적으로 직교좌표계(Cartesian coordinate system, Descartes coordinate system)와 극좌표계(원형좌표계, polar coordinate system)가 있습니다.
2.2. 2차원 직교좌표계
2차원 직교좌표계의 두 좌표축(axis)은 직각으로 위치하며 두 좌표축은 서로 영향을 주지 않는 독립을 나타냅니다.
개체의 표현
변수값의 속성이 범주형이 아니라 이산형이나 연속형과 같은 수치를 나타내는 경우, 이때의 변수값을 변량(variate)이라고 합니다. 변량은 간격척도나 비례척도가 적용된 관측도구로 측정되어 양적 데이터가 됩니다. 변량은 수치로 실현되는 변수값을 의미합니다. 따라서, 변량은 좌표계에서 점으로 표현할 수 있습니다.
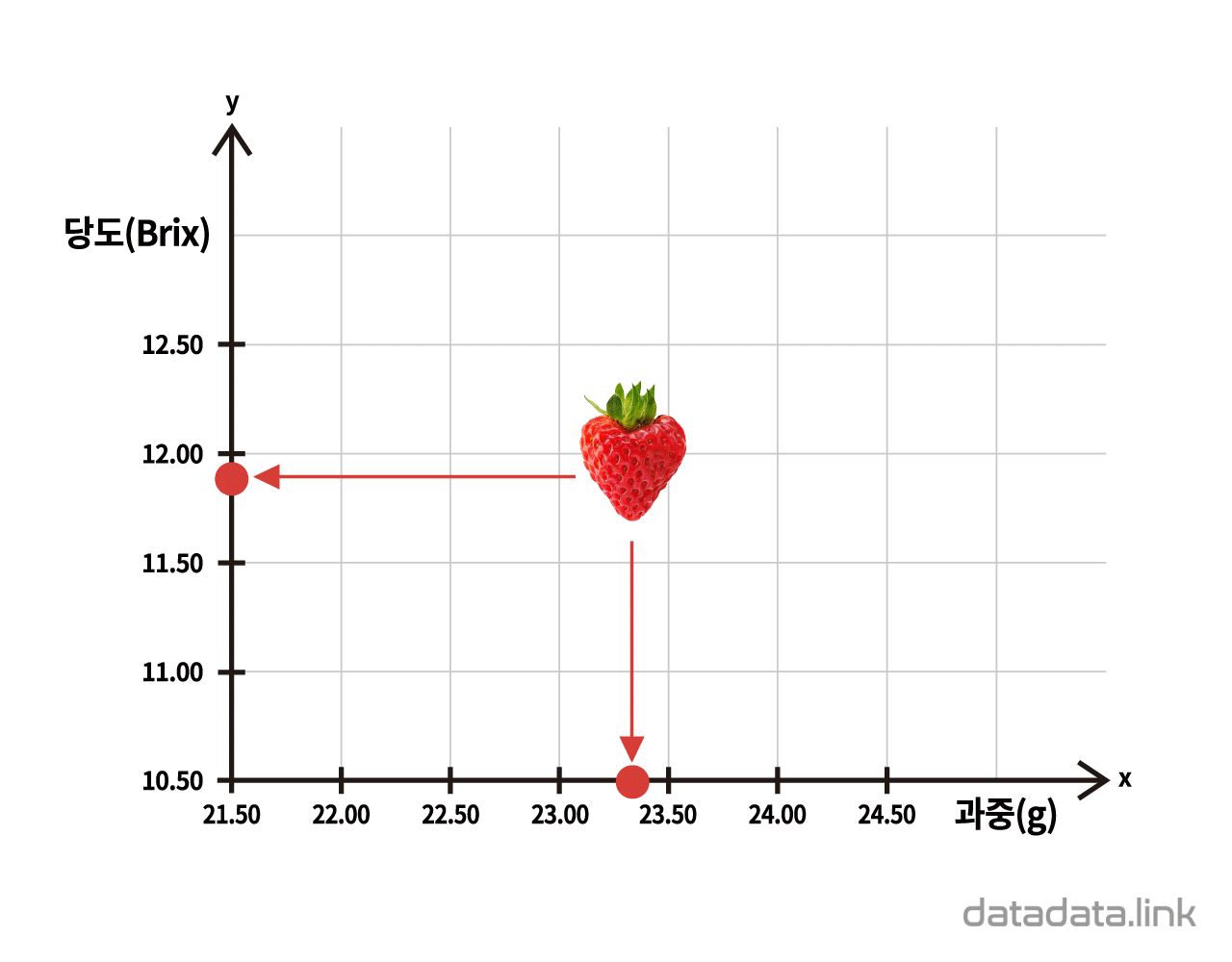
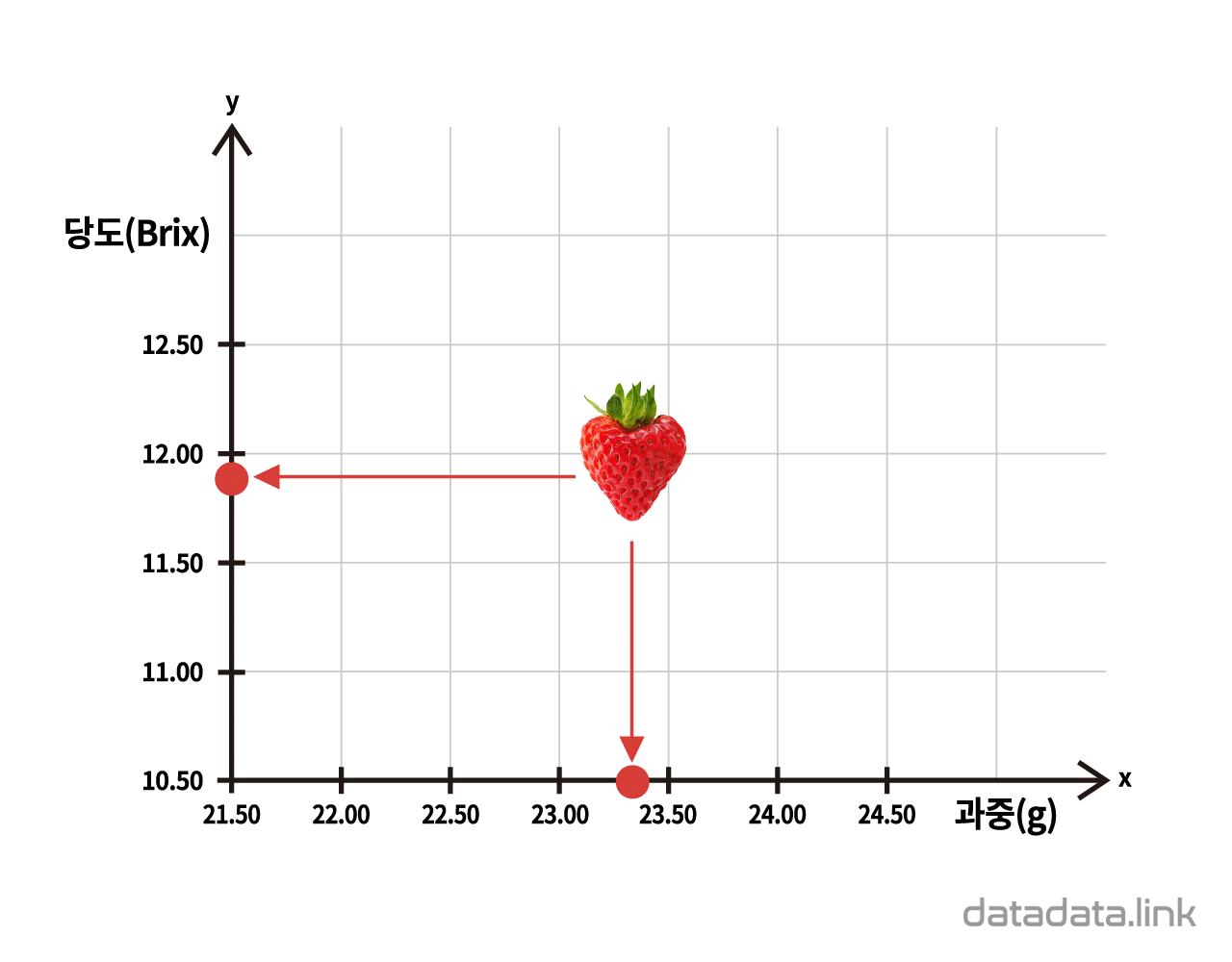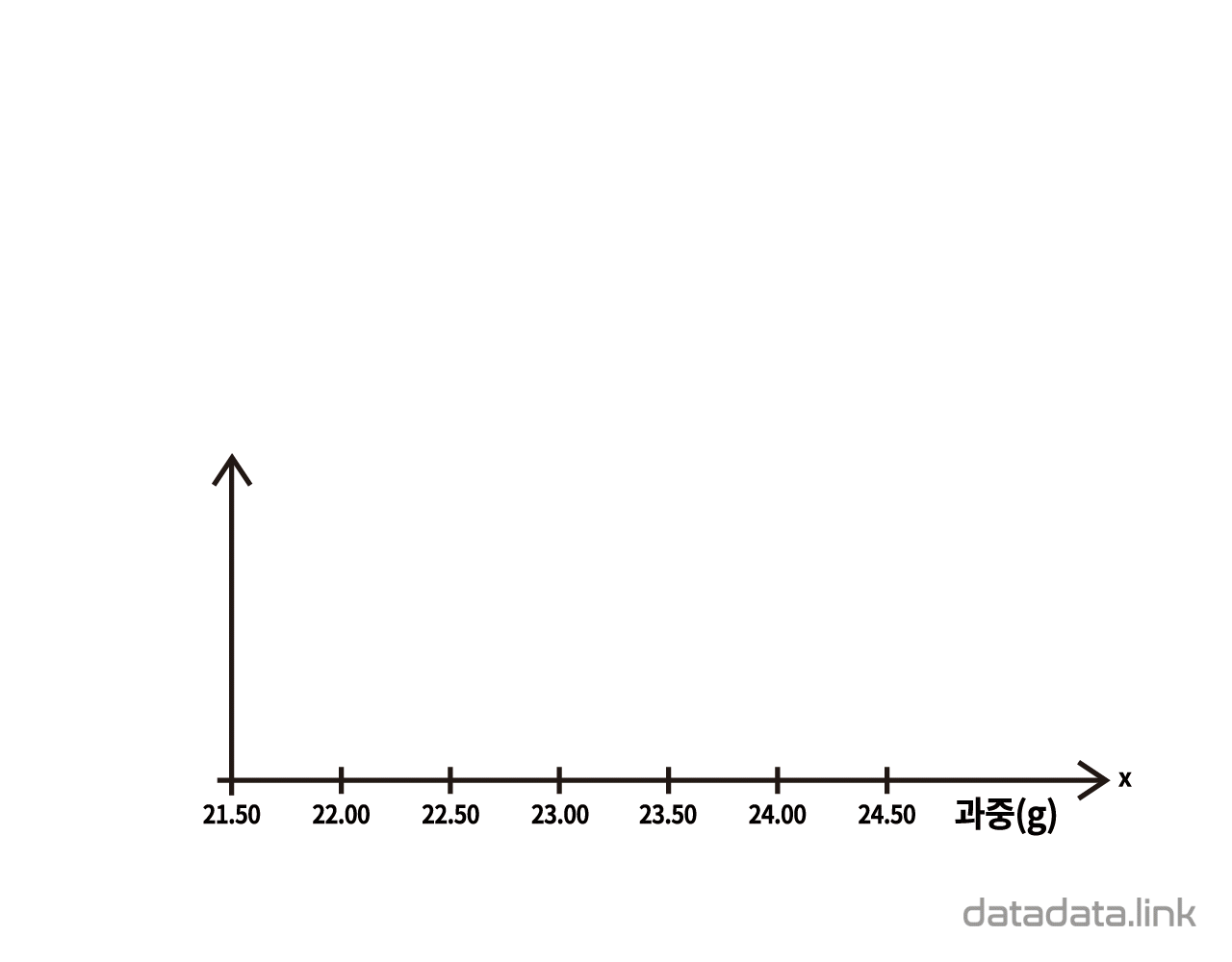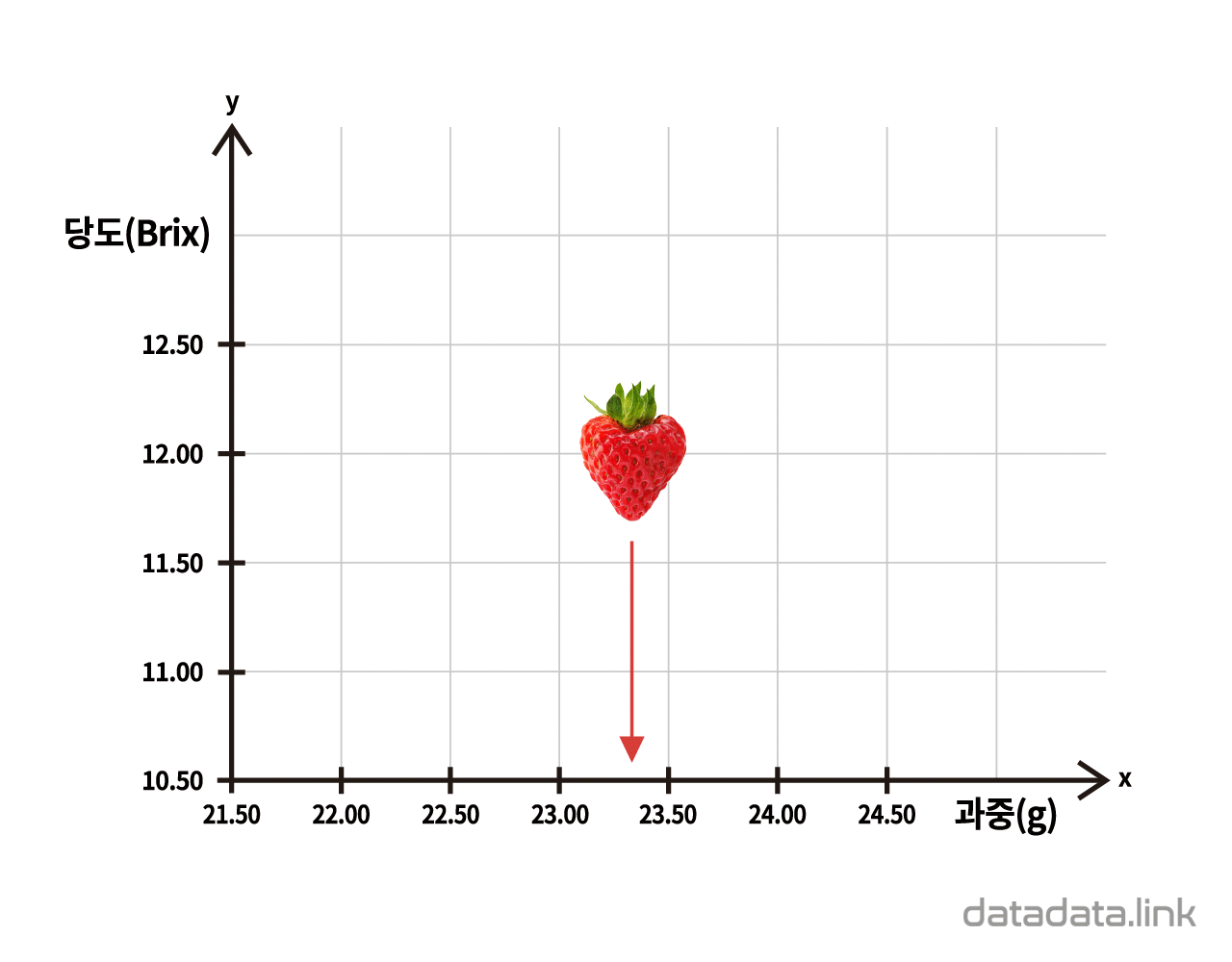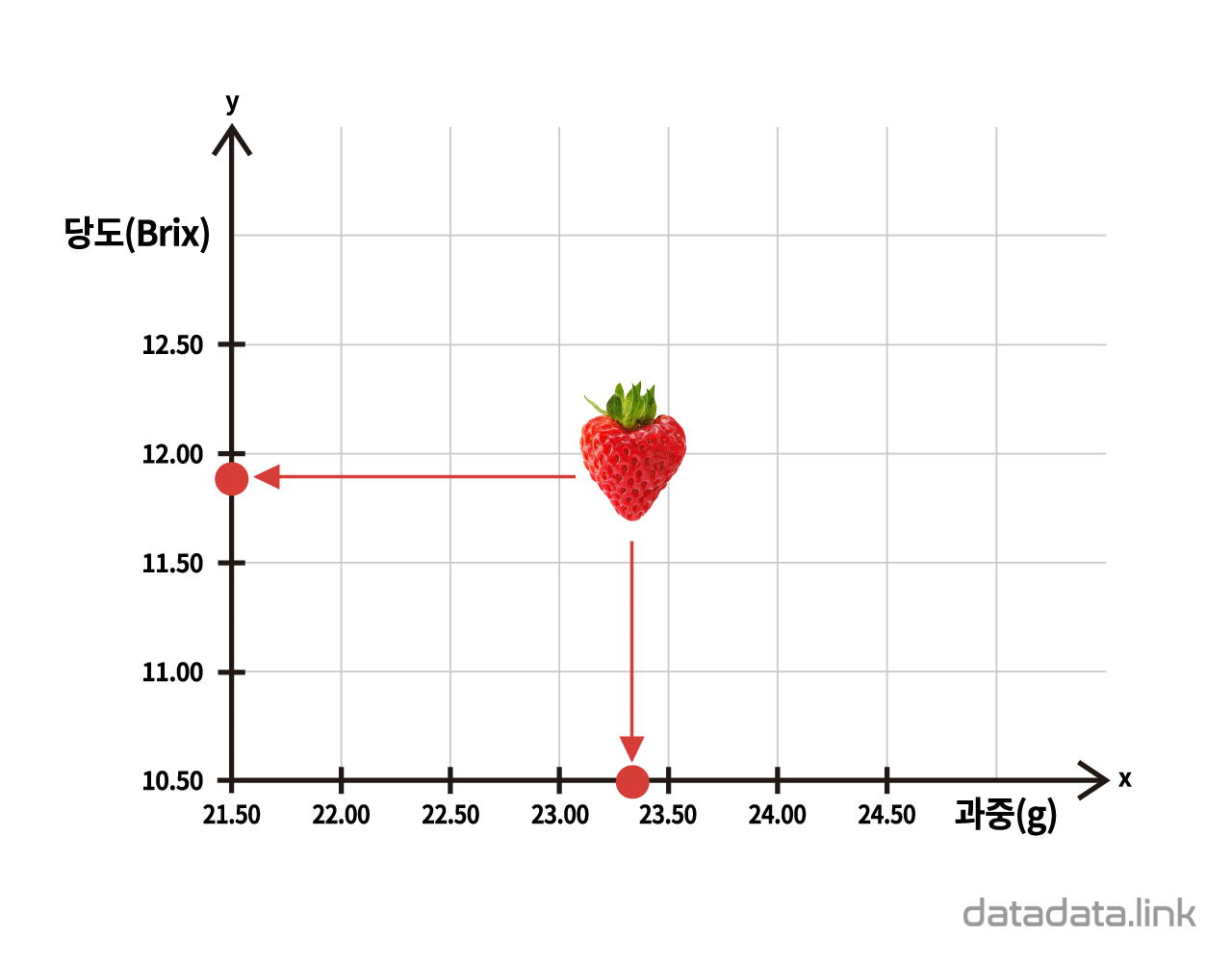
2차원 직표좌표계에 위치한 한 점은 두 좌표값으로 표현할 수 있습니다. 2차원 직교좌표계의 한 점은 좌표축(coordinate axes)에 투영할 수 있습니다. 이때 투영한 점이 좌표축의 좌표(coordinates)가 됩니다. 그리고 0을 기준(origin)으로 양수는 값이 증가하는 방향에 있고 음수는 양이 감소하는 방향에 있습니다. 정리하면 2차원 직교좌표계에 있는 한 점은 두 개의 변수값을 가지며 특별히 변수값의 속성이 수치인 경우, 두 변량을 가집니다.
예를 들어 딸기를 범주명으로 본다면 그 범주에 포함되는 개체를 딸기ID로 구분할 수 있습니다. 딸기 개체는 당도와 과중이라는 속성을 가지고 그 속성을 변수(variable)로 모델링할 수 있습니다. 이때 딸기 개체를 점(point)으로 생각한다면 딸기의 속성인 당도와 과중을 두 축으로 하는 2차원 직교좌표계를 사용하여 딸기 개체를 점으로 표현할 수 있습니다.
집단의 표현
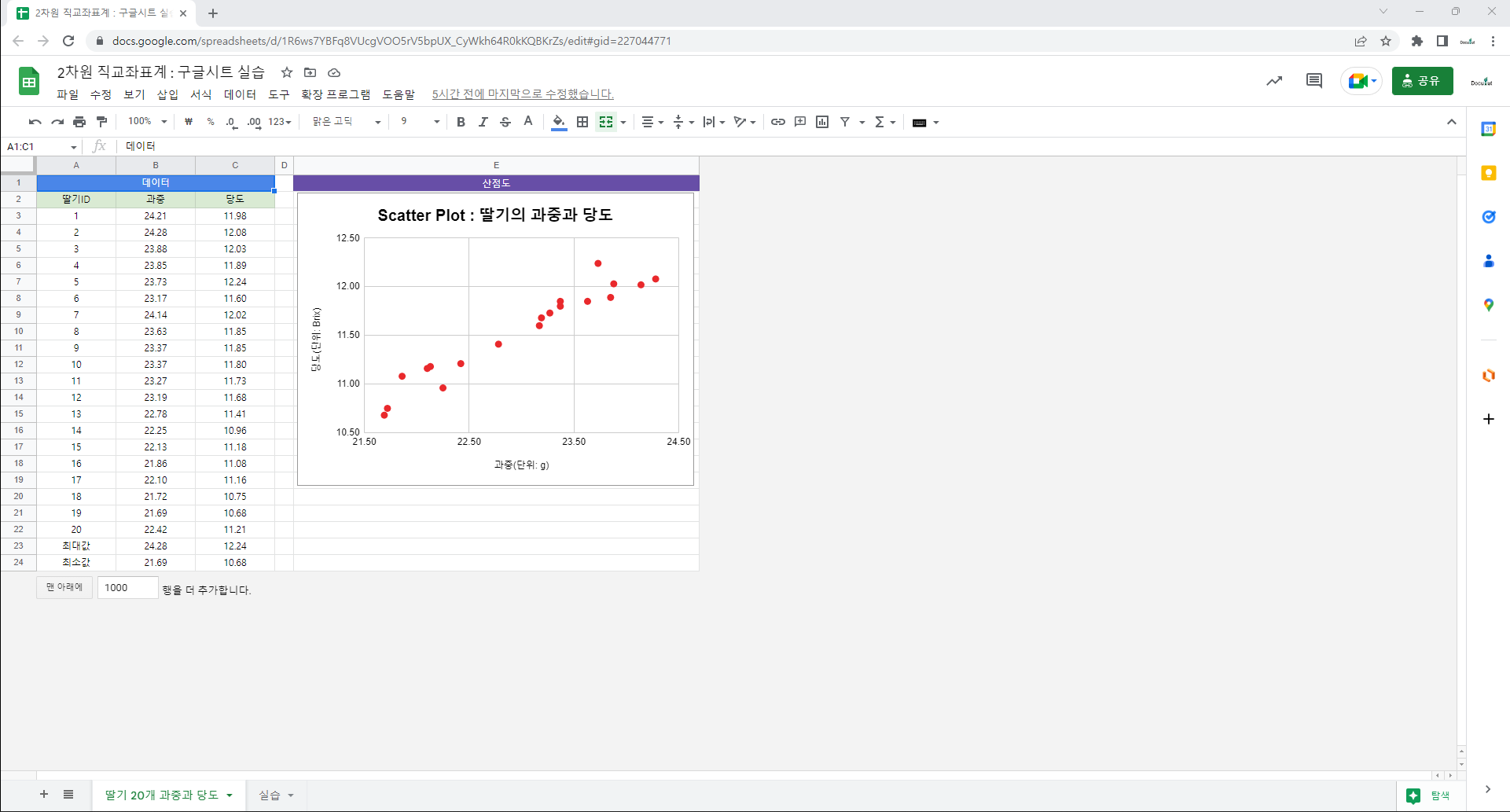
개체를 개체의 속성이 만드는 공간의 점으로 모델링하여 개체가 모인 집단을 산점도로 집단을 시각화할 수 있습니다. 예를 들어 딸기 집단을 딸기의 속성인 과중과 당도가 만드는 2차원 직각좌표계에서 점의 집합으로 표현할 수 있으며 이를 2차원 산점도라고 합니다.
1개의 독립변수와 종속변수의 관계를 나타내는 함수(function)를 표현할 때, 함수는 총 2개의 변수로 표현되므로 2차원 직교좌표계를 사용하여 시각화 할 수 있습니다. 함수를 서로 직교하는 좌표축에서 표현할 때, 연속형 함수는 연속적으로 이어진 점들의 집합으로 그려집니다.
2.3. 2차원 극좌표계
2차원 극좌표계는 원점(origin)에서의 거리(radius)와 거리를 나타내는 방향(radial direction)과 그 방향의 기준이 되는 극축(polar axis)과의 각도가 좌표입니다. 여기서, 극축은 원점에서 시작되며 보통 가로선으로 표현합니다. 정리하면, 극좌표계는 원점의 위치와 원점의 방향이 기준이 되며 원점의 위치에서의 거리와 원점의 방향(극축)과의 각도가 좌표가 됩니다. 2차원 극좌표계에서는 원점에서의 거리와 극축에서의 각도 1개를 좌표로 가집니다. 참고로 3차원 극좌표계에서는 각도가 2개의 좌표로 구성됩니다. 극좌표계에서는 직교좌표계와 마찬가지로 좌표는 서로 영향을 주지 않는 독립입니다.
개체의 표현
변수값의 속성이 범주형이 아니라 이산형이나 연속형과 같은 수치를 나타내는 경우, 이때의 변수값을 변량(variate)이라고 합니다. 변량은 간격척도나 비례척도가 적용된 관측도구로 측정되어 양적 데이터가 됩니다. 변량은 수치로 실현되는 변수값을 의미합니다. 따라서, 변량은 좌표계에서 점으로 표현할 수 있습니다.
2차원 극좌표계에 위치한 한 점은 두 좌표값인 거리와 각도로 표현할 수 있습니다. 2차원 극좌표계의 한 점은 원점에서의 방향과 거리로 표현한다고 할 수 있고 모두 양수입니다. 는 데 특히, 점들의 집합을 이루는 점들의 원점과의 거리들은 집합의 퍼짐을 나타내는 측도(measure)로 사용할 수 있습니다. 원점을 0으로 한다면 거리는 항상 양수이고 각도는 회전방향에 따라 양수 또는 음수로 표현되며 0($0$rad)과 1회전($2\pi$rad) 사이의 수치로 계량화합니다.
예를 들어 딸기를 범주명으로 본다면 그 범주에 포함되는 개체를 딸기ID로 구분할 수 있습니다. 딸기 개체는 당도와 과중이라는 속성을 가지고 그 속성을 변수(variable)로 모델링할 수 있습니다. 이때 딸기 개체를 점(point)으로 생각한다면 딸기의 속성인 당도의 제곱과 과중의 제곱의 합의 제곱근은 원점에서의 거리이고 이 거리는 의미가 있을 수 있습니다. 한편 딸기 개체의 두 속성을 당도와 출하월이라 한다면 당도는 항상 양수이므로 원점에서의 거리($r$)로 모델링하고 출하월은 1년이라는 주기성을 가지므로 각도($\theta$)로 모델링한다면 극좌표로 표현할 수 있습니다.
$$\text{딸기ID}=(r, \theta)$$
여기서, $r$은 당도
$\theta$는 출하월
집단의 표현
개체를 개체의 속성이 만드는 공간의 점으로 모델링하여 개체가 모인 집단을 산점도로 집단을 시각화할 수 있습니다. 예를 들어 딸기 집단을 딸기의 속성인 과중과 출하월이 만드는 2차원 극좌표계에서 점의 집합으로 표현할 수 있으며 이를 2차원 산점도라고 합니다.
극좌표계에서 원을 나타내는 함수의 표현
원의 중심이 원점인 ($0. 0$)에 있고 반지름이 $r$인 원의 경우, 극좌표계에서의 표현식은 다음과 같습니다. 모든 점에서 원점에서의 거리가 일정함을 표현하고 있습니다.
$$\rho=r$$
여기서, $\rho$는 원점으로부터의 거리
$r$은 원의 반지름
원의 중심이 극좌표계에서 ($r_0,\theta_0$)에 위치하고 반지름이 $r$인 경우, 원의 방정식은 다음과 같이 나타낼 수 있습니다.
$$\rho^2 – 2r_0\rho\cos(\theta – \theta_0) + r_0^2 = r^2$$
여기서, $\rho$는 원점으로부터의 거리
$r$은 원의 반지름
($r_0,\theta_0$)는 원의 중심
3. 실습
3.2. 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
3.3. 실습강의
– 실습강의 목차
– 데이터
– 범위
– 산점도