딸기의 과중과 당도를 측정하고, 엑셀을 이용하여 평균과의 편차를 구한 후 상관계수를 계산합니다.

엑셀은 별도의 프로그램 설치가 필요합니다. 여기에서는 엑셀과 사용방법이 동일한 구글시트로 딸기의 당도와 과중의 상관관계를 분석해보겠습니다. Chrome에서 아래의 구글시트 가져가기를 하시면, 직접 실습을 해보실 수 있습니다. 

딸기의 과중과 당도의 대표값을 구하고, 각 딸기의 과중과 당도가 평균으로부터 얼마나 차이가 나는지를 구합니다.

average 함수를 이용해서, 과중과 당도의 대표값 중 산술평균을 구합니다. 각 딸기의 당도와 당도 평균, 과중과 과중 평균의 편차를 각각 구합니다.

과중과 당도의 편차의 곱 합계와 과중 편차제곱 합계의 비율이 회귀선의 기울기가 됩니다.

과중을 X축으로 하고, 당도를 Y축으로 하는 산점도 상에 회귀선을 그리게 되면, 그 기울기는 과중이 변화할 때 당도가 얼마나 변화하는지를 나타냅니다. 이는 과중과 당도의 편차의 곱 합계를 과중 편차제곱 합계로 나눈 값이 됩니다.

과중과 당도의 상관계수가 유의한지는 표본의 크기, 상관계수에 의해 좌우됩니다.

딸기 20알의 과중과 당도의 상관계수가 유의미한지를 검정하기 위해, 검정통계량 t를 구합니다. t분포 상에서 검정통계량의 확률밀도를 구하고, 그것이 유의수준보다 작으면, 과중과 당도의 상관관계가 유의하다고 할 수 있습니다.

회귀선은 상관관계를 가지는 두 변수를 대표하는 정보를 나타내지만, 각 딸기와 회귀선과의 거리(분포정도)에 대한 정보를 가지고 있지는 않습니다.

위의 예에서, 딸기 500알의 당도와 과중 데이터는 딸기 ID 500개, 당도 500개, 과중 500개를 합하면 모두 1,500개가 됩니다. 1,500개의 데이터를 기울기와 절편이라는 2개의 값으로 나타낸 것이 회귀선입니다. 회귀선을 이용하면, 큰 데이터를 간단하게 표현할 수 있는 반면, 회귀선으로부터 각 딸기와의 거리, 잔차에 대한 정보는 잃게 됩니다. 

변수란 변하는 것입니다.

영어로는 Variable 입니다. 변하는 것에 이름을 붙인 것이 변수명입니다.

예를들면  500알의 딸기의 당도를 측정하면,  당도는 500개의 숫자로 이루어 집니다. 이와 같이 변하는 “당도”를 변수라고 합니다. 변수의 이름을 “딸기의 당도”로 하면 이해가 쉽겠지요. 그리고 수식에 사용하는 변수명은 x와 y등 알파벳 기호를 많이 사용합니다. 

1개의 동전의 양면에 각각 0과 1을 쓰고, 동전을 바닥에 던져서 위로 향한 숫자를 보면   0 혹은 1이 나오게 됩니다. 즉, “윗면의 수”를 변수로 한다면  변수가 가지는 값은 0과 1로만 구성됩니다.

확장해서, 동전 4개의 양면에 각각 0과 1을 쓰고, 동전을 바닥에 던져서 위로 향한 숫자를 더하면  0, 1, 2, 3, 4 다섯개 숫자 중에서 하나가  됩니다. 여기서 변수를 “동전 3개를 던져서 나타난 동전 윗면의 합”이라고 할 수 있습니다.

동전의 앞면과 뒷면이 나올 확률이 반반인 동전 4개를 여러번 던지다 보면, 경험을 통해 윗면의 합이  2가 나올 확률이 0이나 4가 나올 확률보다 높다는 것을 알 수 있습니다.

확률변수란 확률을 가지는 변수입니다.

“설의 당도”라는 변수는 0에서 100사이에 반드시 존재하기에 확률변수입니다.

“설”이라는 품종의 딸기 중 500개의 딸기를 표본추출해서 당도를 측정해본 결과  “설의 당도”는 9.64부터 12.96 사이에 95%가 존재하며, 이 범위를 벗어나는 것은 5%라는 결과를 얻게 되었습니다.  “설의 당도”는 확률변수이기 때문에 합해서 항상 100%가 됩니다. 

변수의 상대적인 개념은 상수입니다.

우리가 추출한 표본의 평균과 분산은 표본을 추출할 때마다 변하는 값, 즉 변수입니다. 반대로 표본의 모집단의 평균과 분산은 변하지 않는 상수로 가정하고 모델링을 하는 경우가 많이 있습니다.

변수와 상수의 차이, 변수와 상수의 비율도 변수입니다.

모집단의 평균과 표본평균의 차이, 모집단의 분산과 표본분산의 비율은 표본을 추출할 때마다 변하고, 확률을 가지고 설명할 수 있는 확률변수입니다. 

당도를 기준으로 품종을 판정하기로 합니다.

우리나라의 농림수산식품부 국립종자원에서는 딸기 신품종 심사를 위해 48가지의 특성으로 기존품종과 대조품종을 비교하는 방안을 제시하고 있습니다. 이러한 기준은 현재의 사람들의 인식과 기술수준 등을 고려하여 정하는 것으로 불변의 것은 아닙니다.

소비자들은 과일을 선택할 때, 맛을 기준으로 선택하는 소비자가 대다수입니다. 맛에 영향을 주는 것에는 과일의 당도, 산도, 식감 등이 있는데, 여기에서는 당도를 기준으로 품종을 판정한다고 가정해보겠습니다.

표본의 당도를 측정, 한국딸기와 일본딸기의 평균을 추정해서 비교해보면, 두 딸기는 다른 품종입니다.

두 딸기가 같은 품종인가를 판정하기 위해 두 가지 기준을 정해보았습니다.

품종이 같거나 다름을 판정할 때 당도의 평균과 분포로 판정하기로 합니다.

두 딸기의 같은 품종이라고 가정하고, 같을 확률이 5%보다 낮다면 두 딸기는 다른 품종이라고 하기로 합니다.

12월 25일부터 다음 해 4월 25일까지 총 5번 나온 딸기를 구매해서 각각 100알씩 당도를 측정했습니다. 설 500개의 당도 평균은 11.3 Brix, 표준편차는 0.85이며, 아키 500개의 당도 평균은 10.0 Brix, 표준편차는 1.06입니다.

표본평균, 표본분산, 표본크기로 모평균의 95% 신뢰구간을 구했습니다.

500개씩의 표본으로 추정한, 설의 모집단 당도 평균의 95% 신뢰구간은 11.27~11.42이고, 아키의 모집단 당도 평균의 신뢰구간은 9.89~10.07이다. 두 딸기의 모집단 당도 평균의 95% 신뢰구간이 겹치지 않는다는 것을 알 수 있습니다. 두 딸기는 다른 품종입니다.

설향 vs 아키히메

2018년 평창 동계올림픽에 참여한 일본의 컬링 선수들이 우리나라 딸기를 먹고 극찬한 데 대해, 일본의 농림수산상이 2018년 3월 국무회의에서 “한국 딸기 뿌리는 일본 품종이다”라고 한 사실이 있습니다.

2000년대 초 주로 판매되던 아키히메와 레드펄은 일본 품종으로 주로 3~5월에 수확을 합니다.

2005년 아키히메와 레드펄을 교배하여 개발한 설향이라는 품종은 재배가 쉽고 맛이 좋아 전국의 딸기 재배 농가에 빠르게 퍼져 나갔습니다. 그 결과 2005년 약 9%에 머물던 설향, 매향, 금향 등의 국내 육성종이 2013년 이후에는 우리나라 딸기 재배면적의 78%를 차지하게 되었습니다.

Reference

농림축산식품부, 국립종자원. 2019. 신품종 심사를 위한 작물별 특성조사기준(딸기)

출하일과 당도의 산점도를 그려보면, 12월 25일에 나온 딸기가 가장 맛있습니다.

12월 25일부터 다음 해 4월 25일까지 총 5번 나온 딸기를 구매해서 각각 4알씩 당도를 측정했습니다.

X축은 출하일, Y축은 당도로 산점도를 그렸습니다. 산점도 상에서 12월 25일에 나온 딸기의 당도가 높으면서도 균일하다는 것을 알 수 있습니다.

과중과 당도의 산점도를 그려보면, 딸기는 무거울수록 맛있습니다.

이번에는 딸기의 과중과 당도를 함께 측정했습니다. X축은 과중, Y축은 당도로 산점도를 그려보았습니다. 과중이 클수록 당도가 높다는 것을 알 수 있습니다.  

과중이 1g 늘어나면, 당도는 0.516 브릭스 늘어납니다.

이번에는 딸기의 500알의 과중과 당도를 측정했습니다. X축은 과중, Y축은 당도로 산점도를 그린 후, 과중과 당도의 관계를 대표하는 직선을 그렸습니다.

이 직선의 기울기는 0.516이고 절편은 0.521입니다. 과중이 1 늘어나면, 당도는 0.516이 늘어납니다.

우리나라의 딸기품종 설향은 겨울철에 맛있습니다.

딸기는 전년도 늦가을부터 다음해 초여름까지 재배하면서 4~5번 정도 열매를 수확합니다. 우리나라에서 유통되는 딸기의 70% 이상을 차지하는 설향은 추위에 강합니다. 겨울에 수확하는 설향은 익는데, 시간이 좀 더 걸리고 광합성을 오래함으로써, 봄철에 수확하는 설향에 비해 당도가 높습니다.

위에 사용한 데이터는 설향을 특성을 반영하여 학습용으로 가공한 데이터입니다.

평균 수심 150cm, 강을 건너도 될까요?

군인들이 목적지로 빨리 가기 위해, 눈 앞의 강을 건너야 합니다. 군인들의 키의 평균은 180cm이고, 강의 수심 평균은 150cm라는 정보를 얻게 되었습니다.

지휘관은 모든 군인에게 강을 건널 것을 명령햇습니다. 그런데, 군인들이 한 명, 두 명 물 속에 빠져서 허우적거리는 것을 목격하게 되었습니다. 지휘관은 급히 회군을 명령했습니다.

다시 조사해보니, 이 강의 최대 수심은 200cm이고, 군인 중 키가 200cm를 넘는 사람은 없었습니다.

수심의 최대값이 인간의 키 최대값보다 크기 때문에 강을 건너면 안 됩니다.

범위는 최대값과 최소값으로 표현할 수 있습니다. 수심의 범위는 100~200cm이고, 군인 들 키의 범위는 175~185cm라는 것을 미리 알았다면, 강을 건너지 않고, 다른 선택을 했을 것입니다.

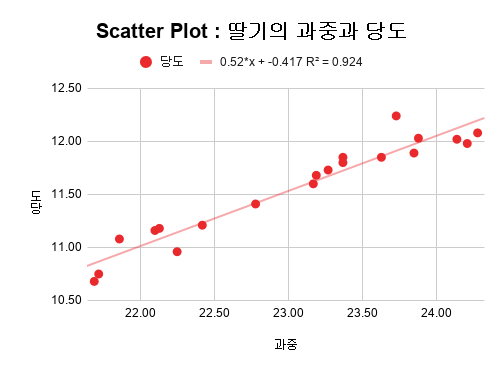
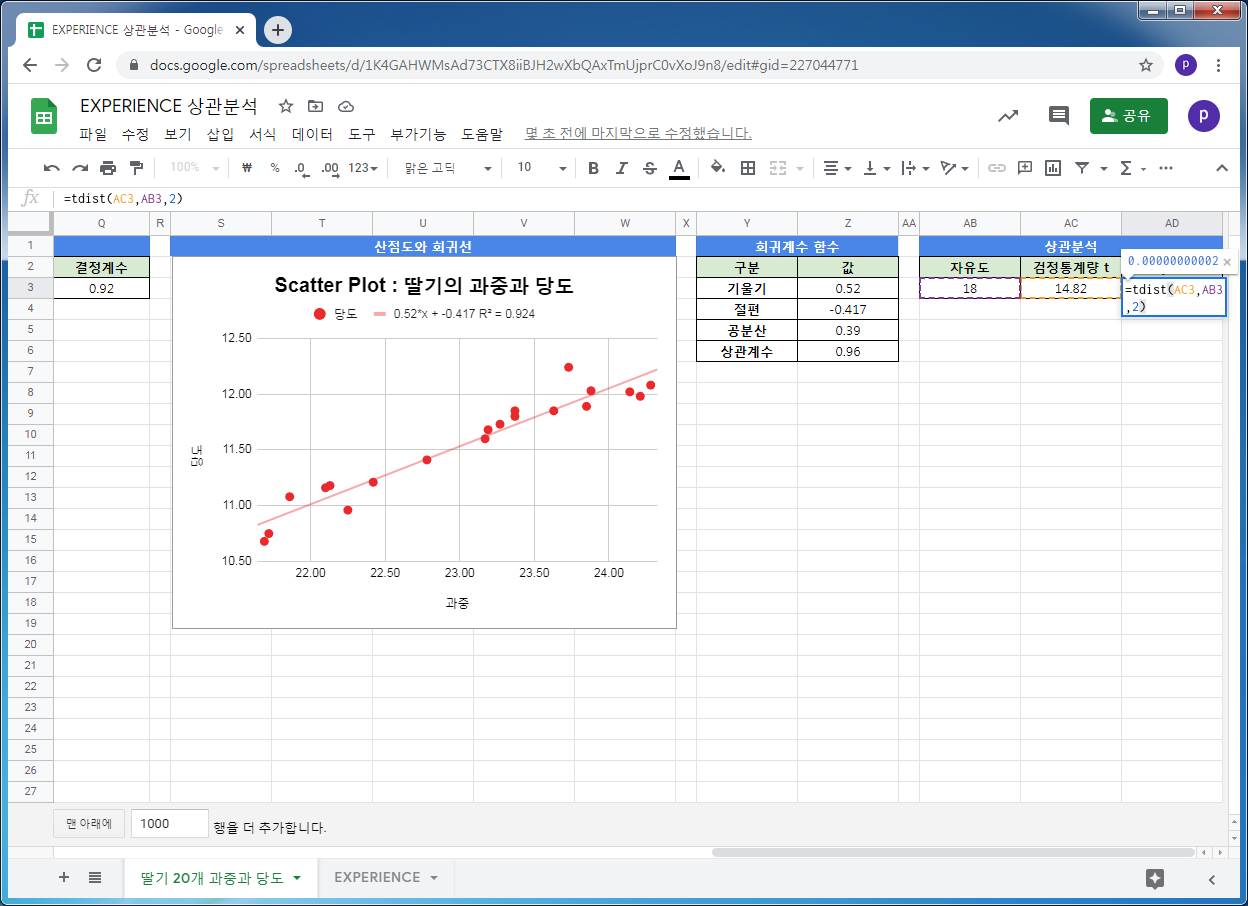
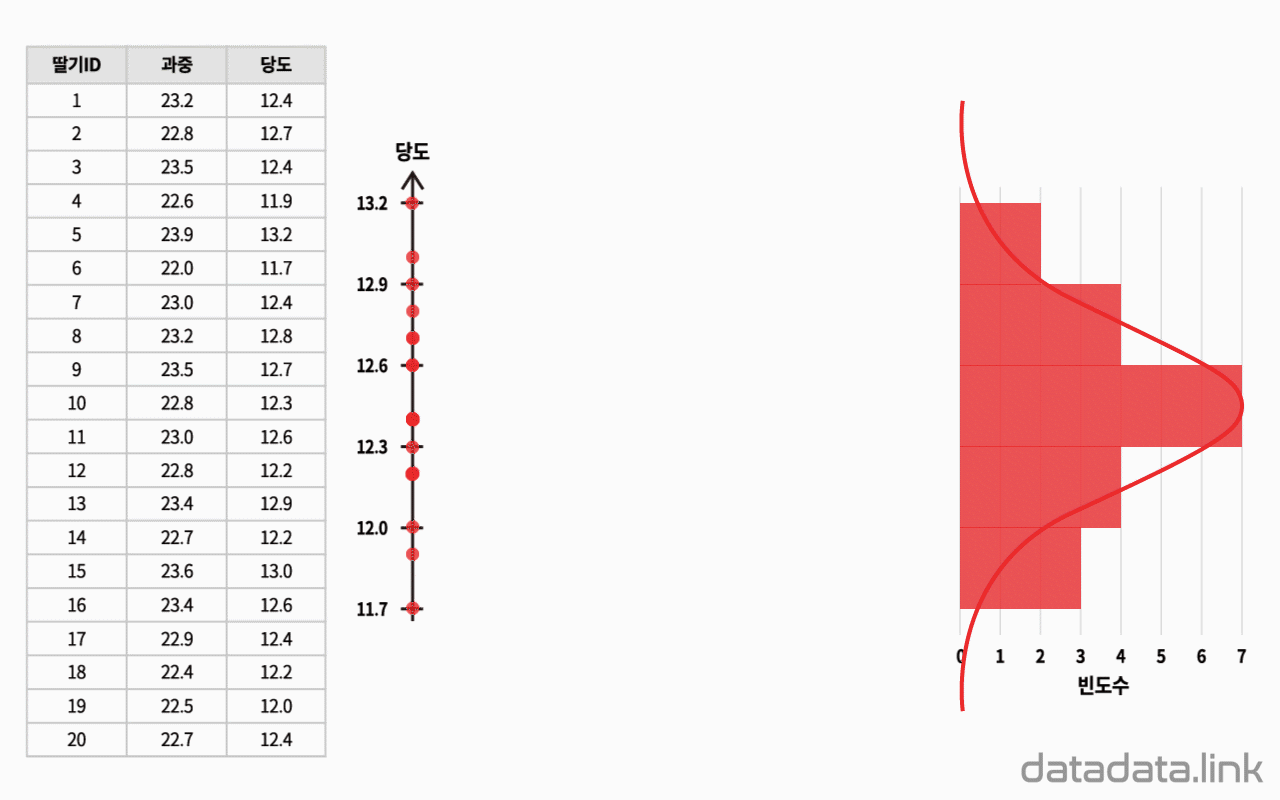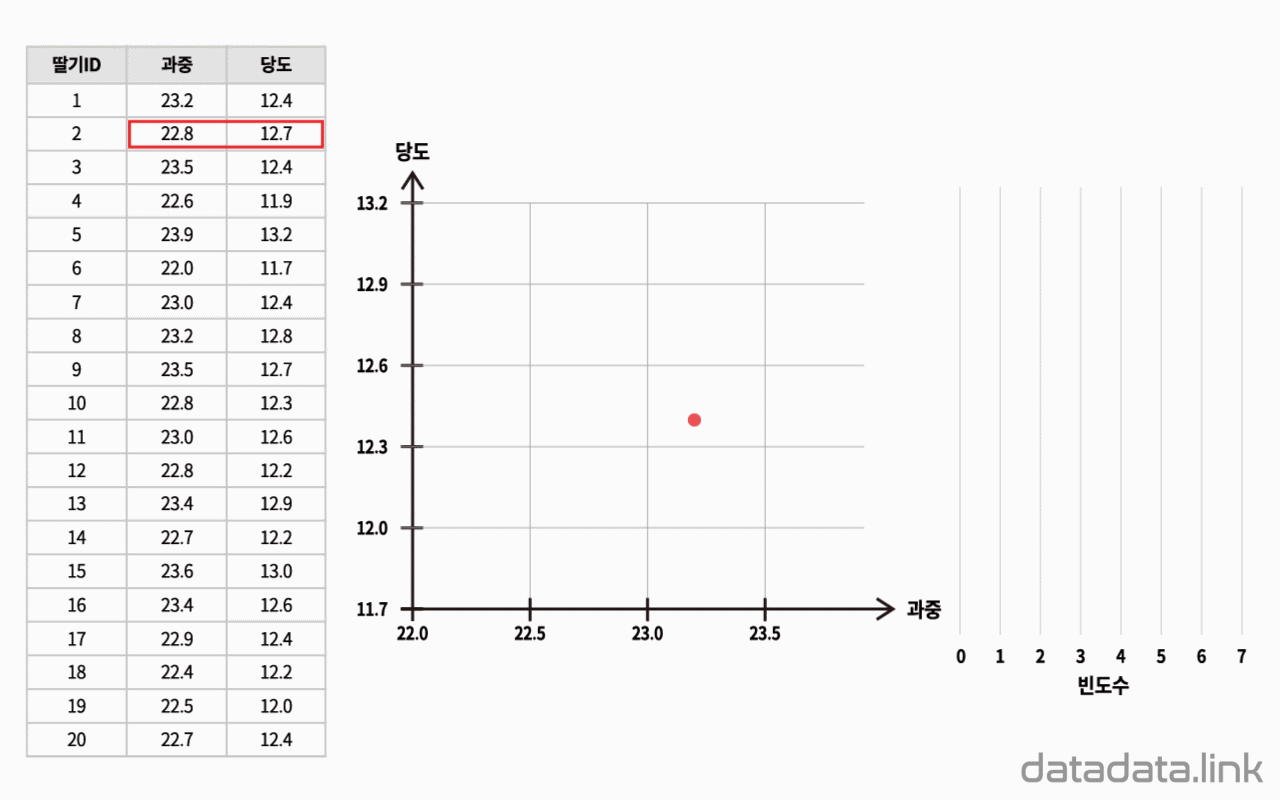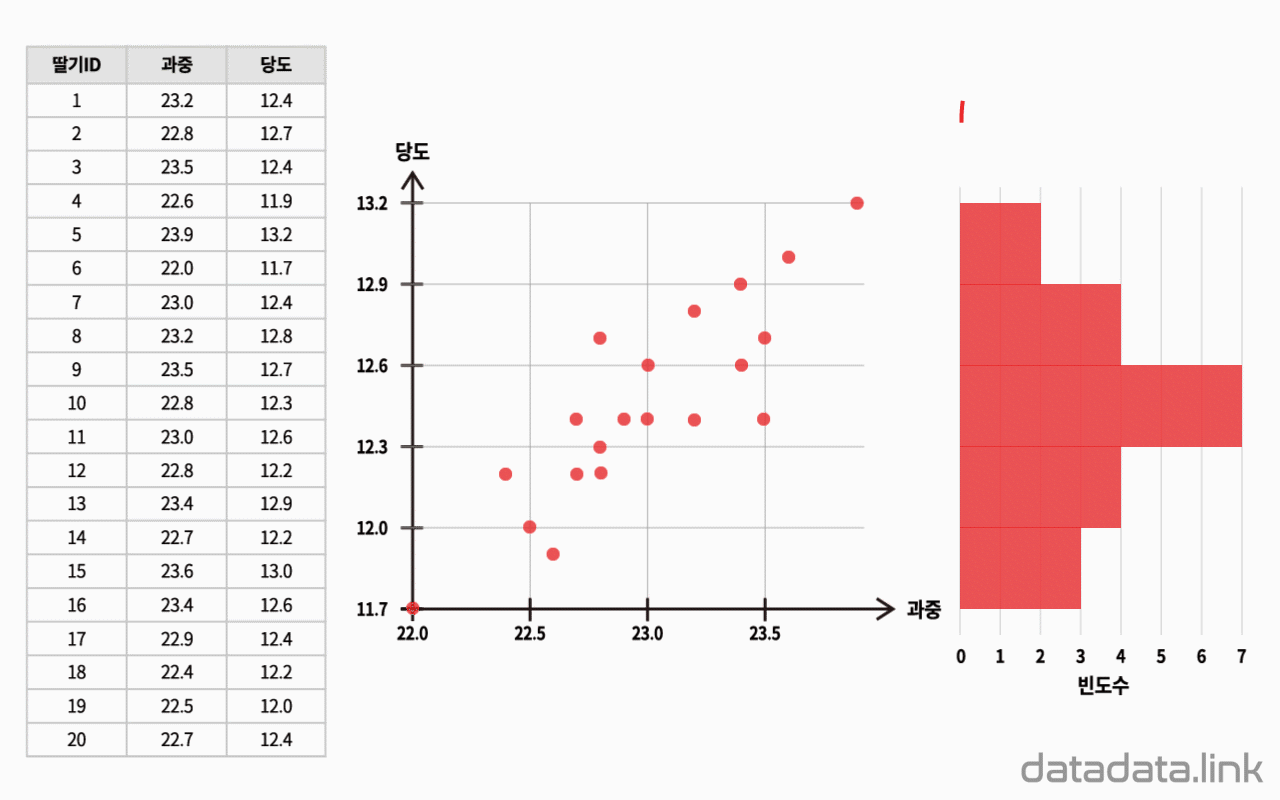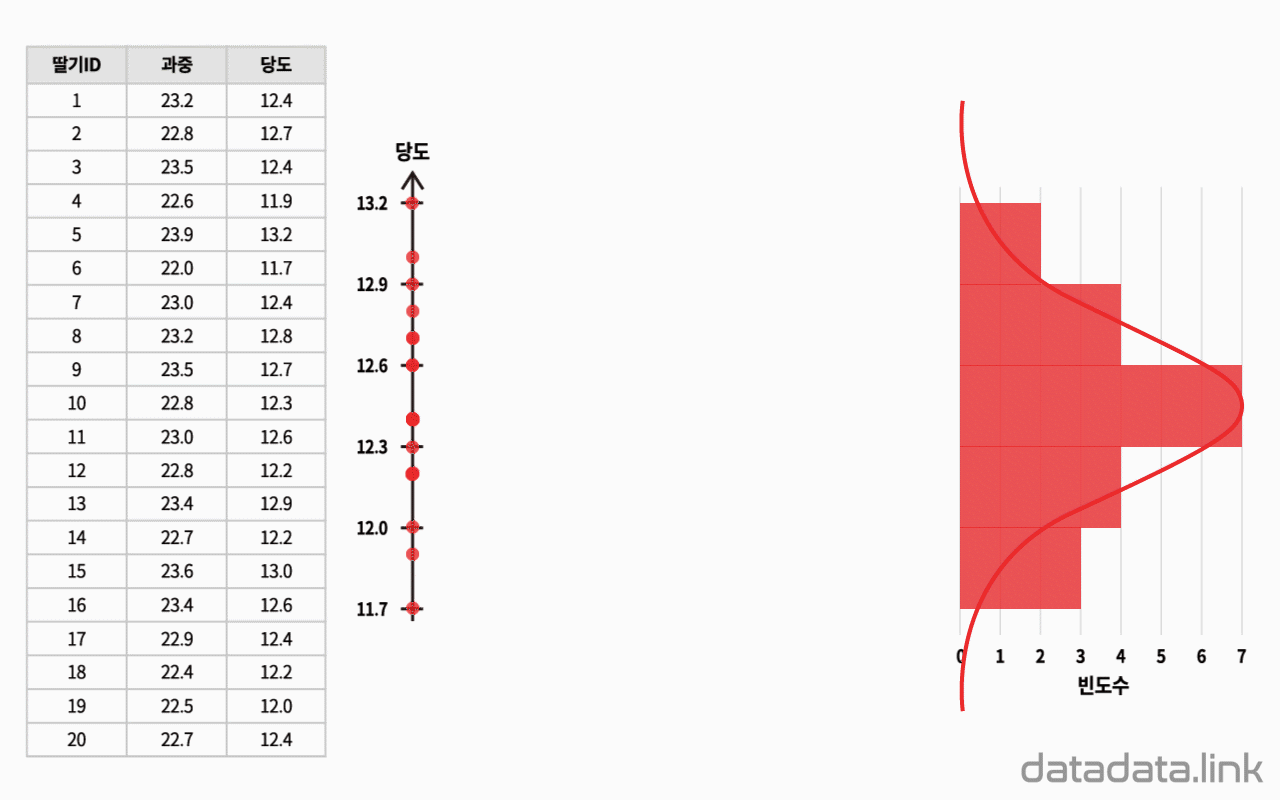
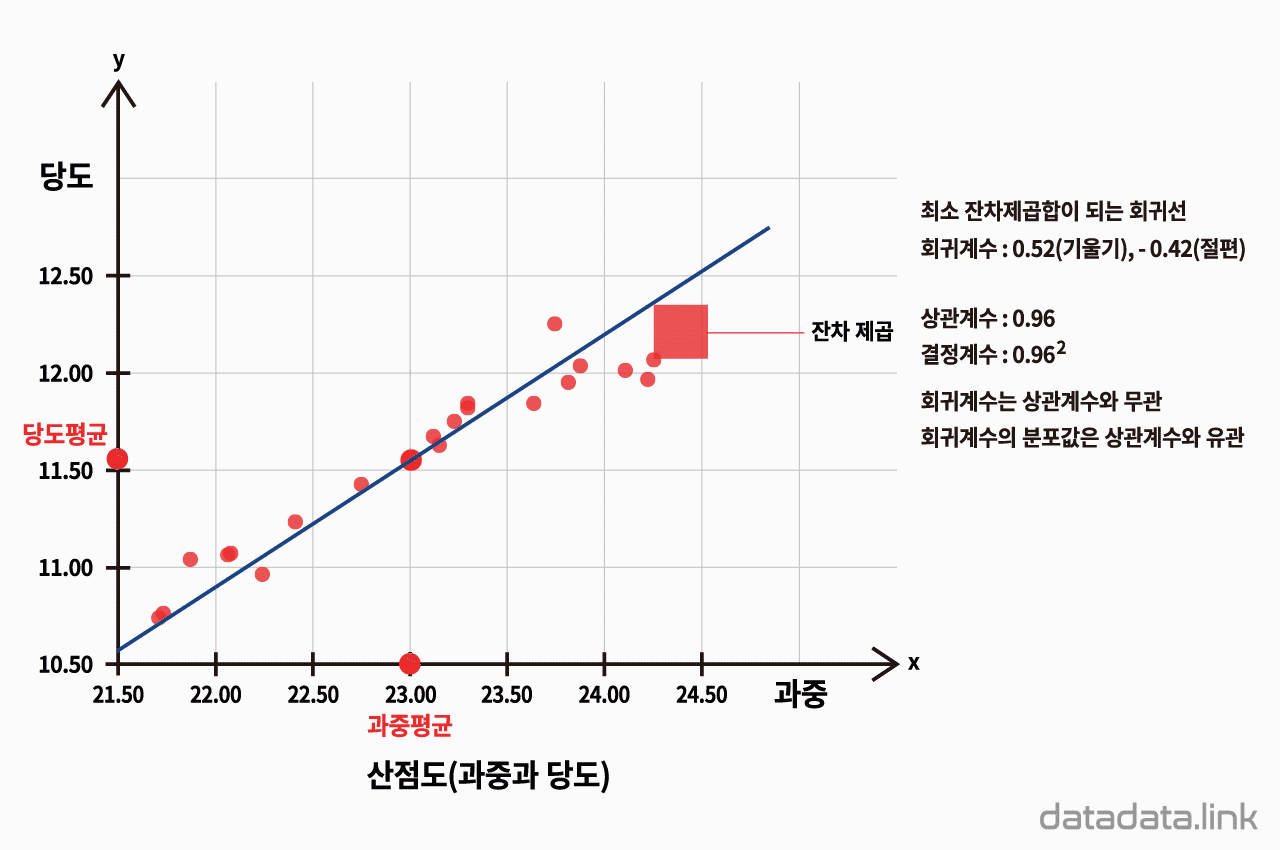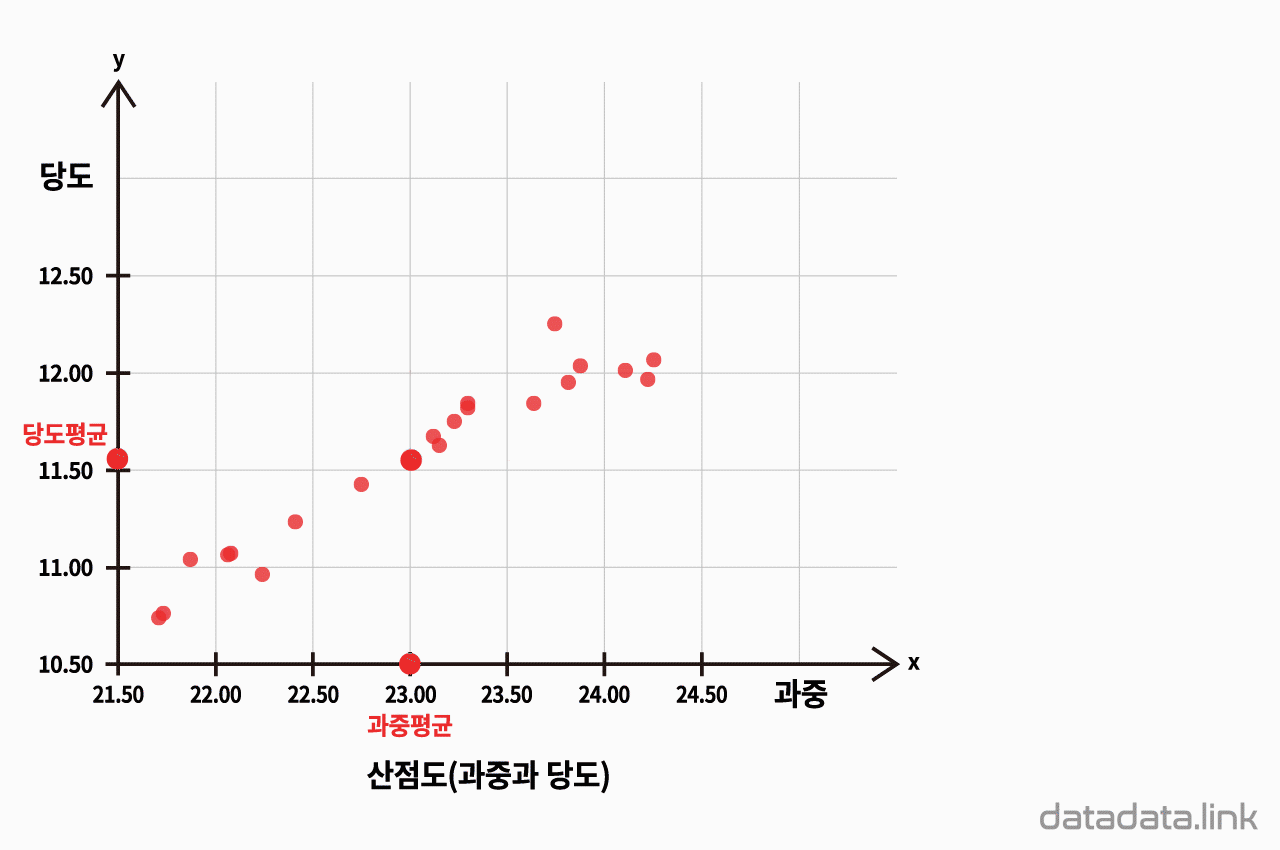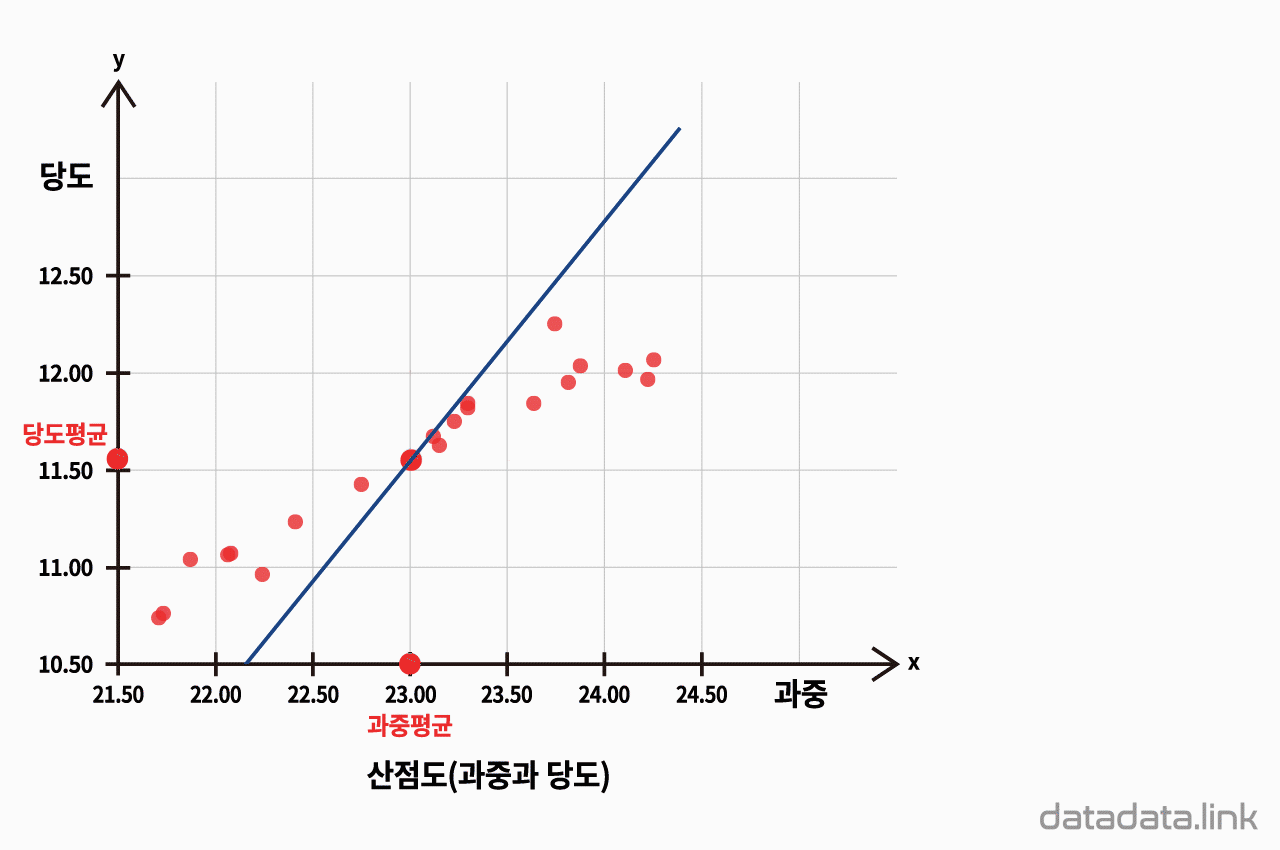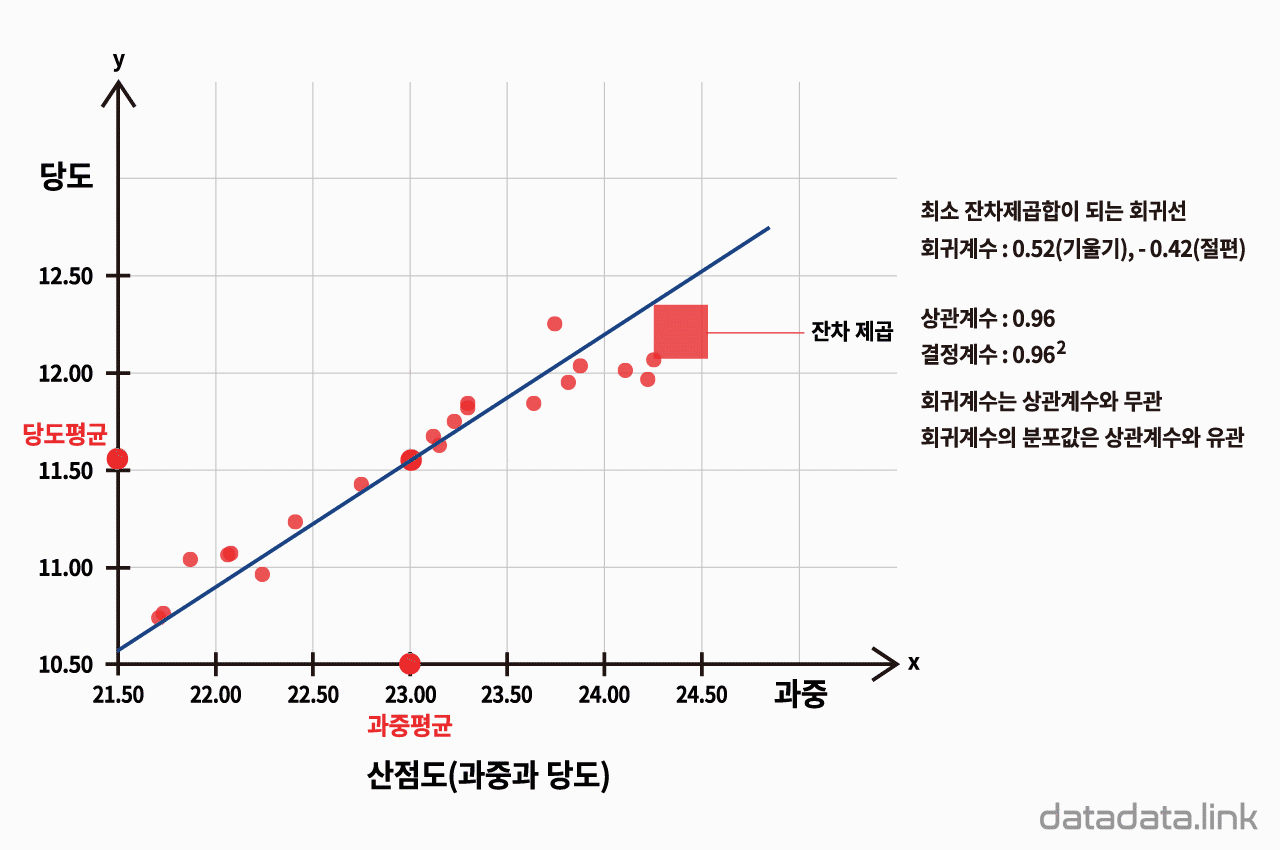
데이터의 분포값은 데이터의 분포정도(measure of dispersion)를 나타냅니다.

산포도(degree of scattering) 또는 변산성(variability)이라고 부릅니다.

데이터의 분포값에는 우선 데이터의 범위(range)가 있습니다.

범위는 최대값과 최소값의 구간으로 표시합니다.

중앙값을 기준으로 흩어진 정도를 수치로 나타내는 것에는 사분위수범위 등이 있습니다.

평균을 기준으로하는 분포정도(measure of dispersion)에는 분산(variance)과 표준편차(standard deviation)가 있습니다.

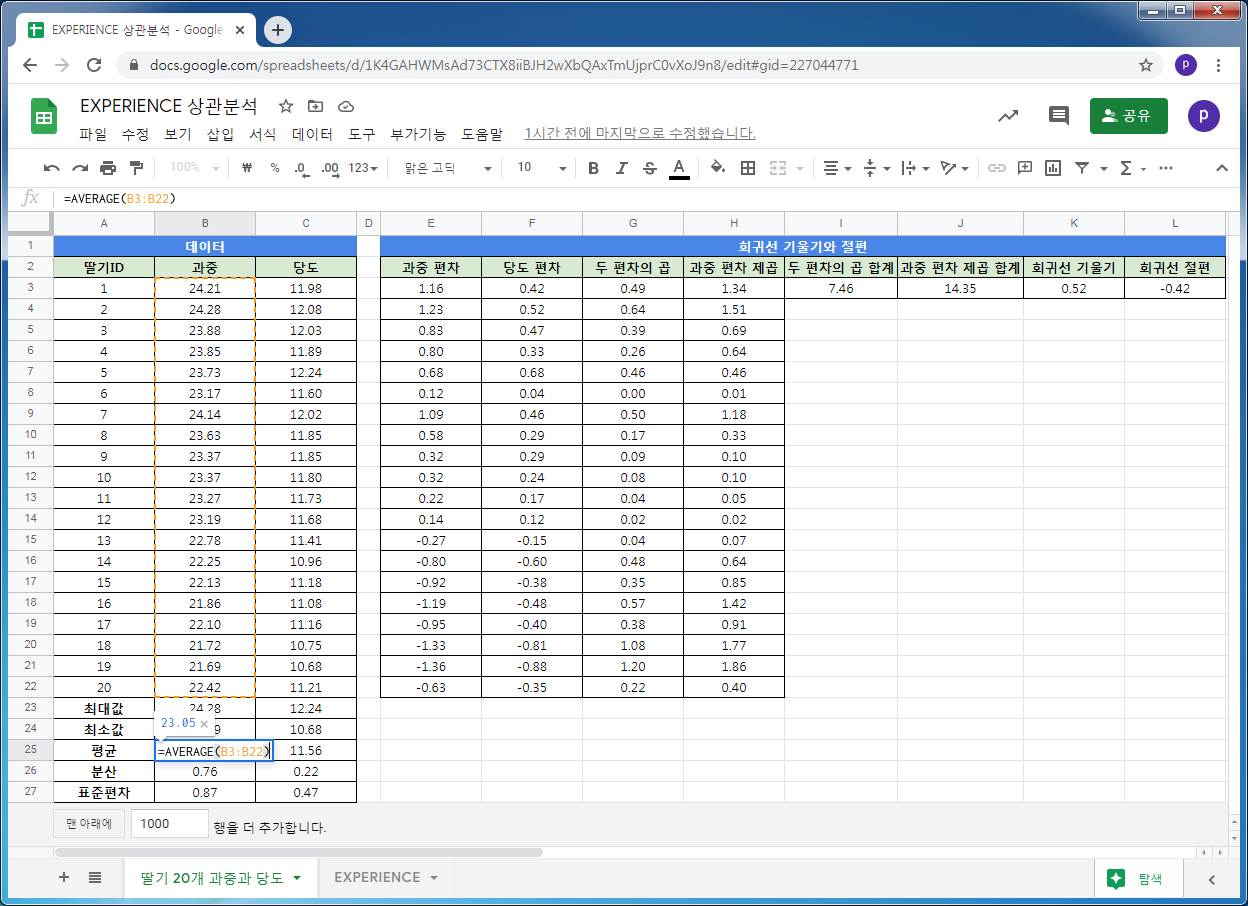
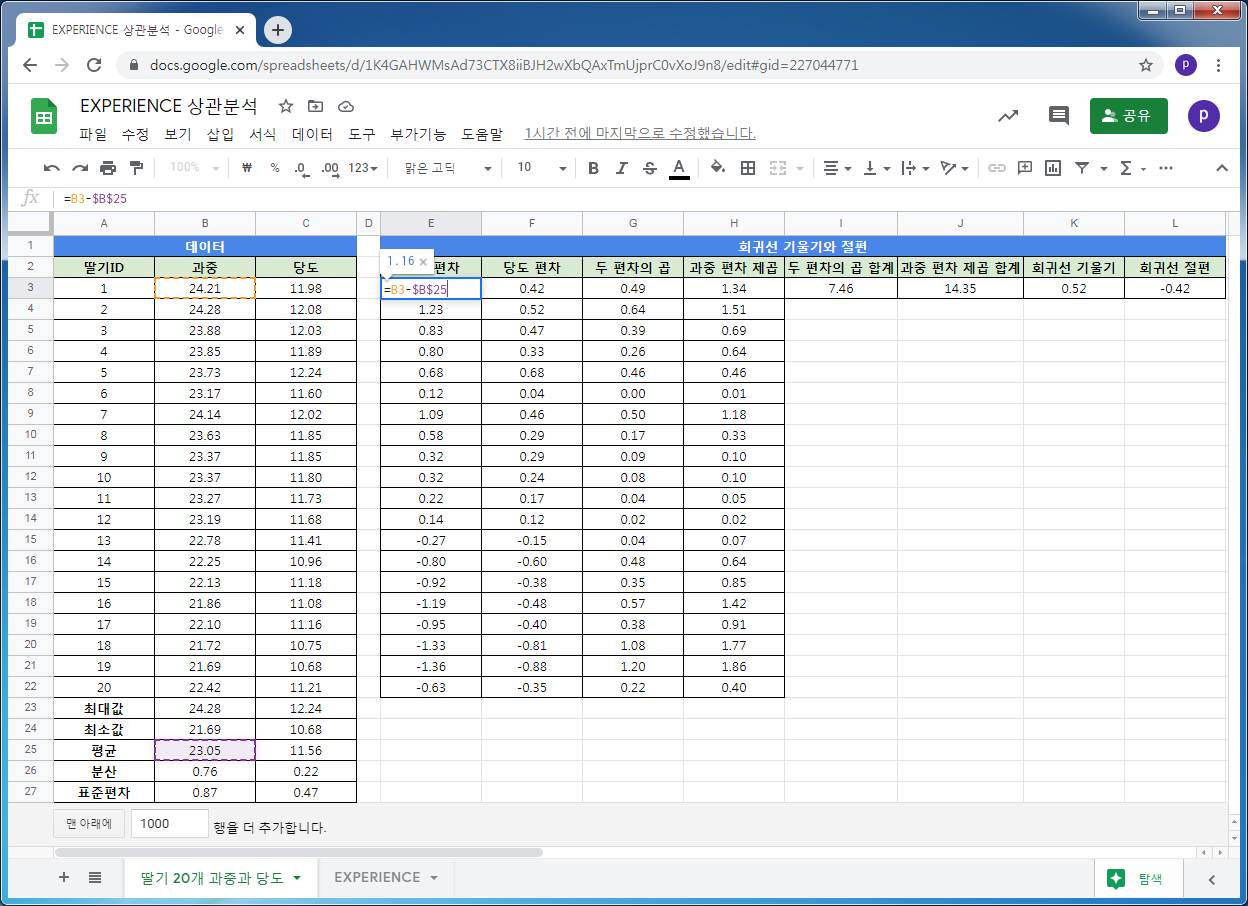
분산(variance)은 각 변수값과 평균과의 차이를 제곱한 값들의 대표값을 구한 것입니다.

즉, 변수값에서 평균을 뺀 값(편차)의 제곱의 평균입니다.

또한, 평균과 변수와의 거리제곱의 평균이라고 표현할 수도 있습니다.

그래서 분산은 0이나 양의 수가 됩니다.

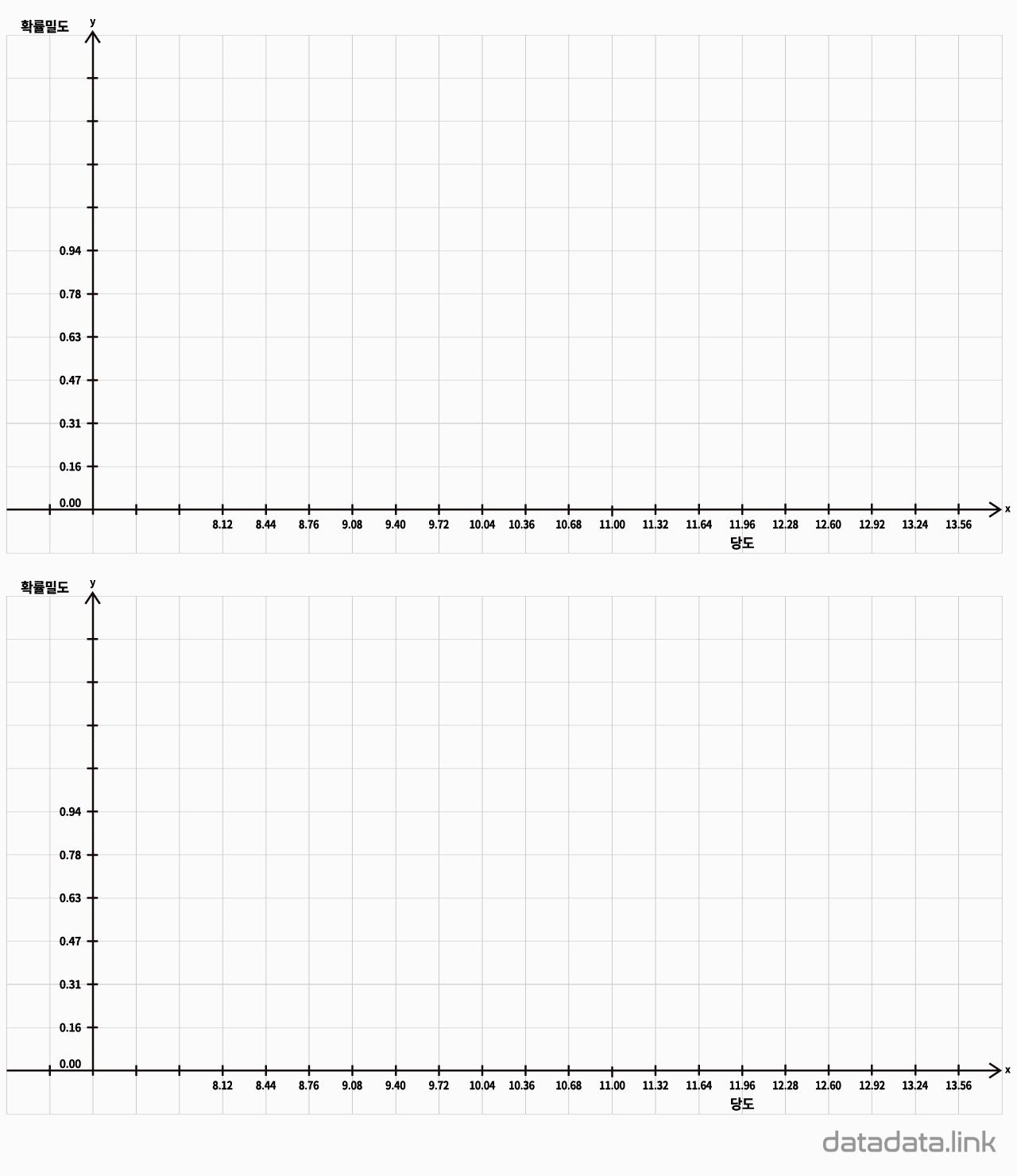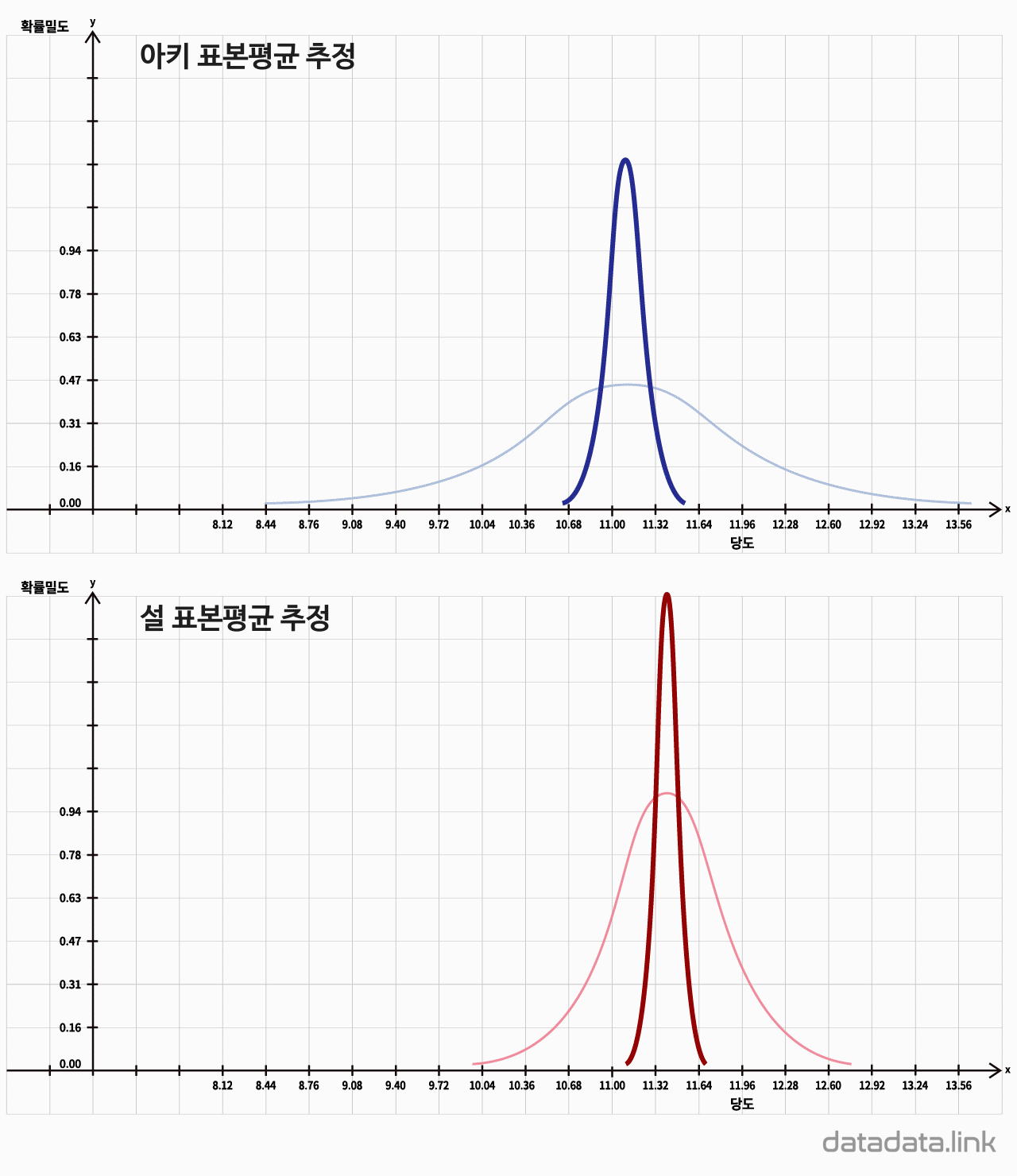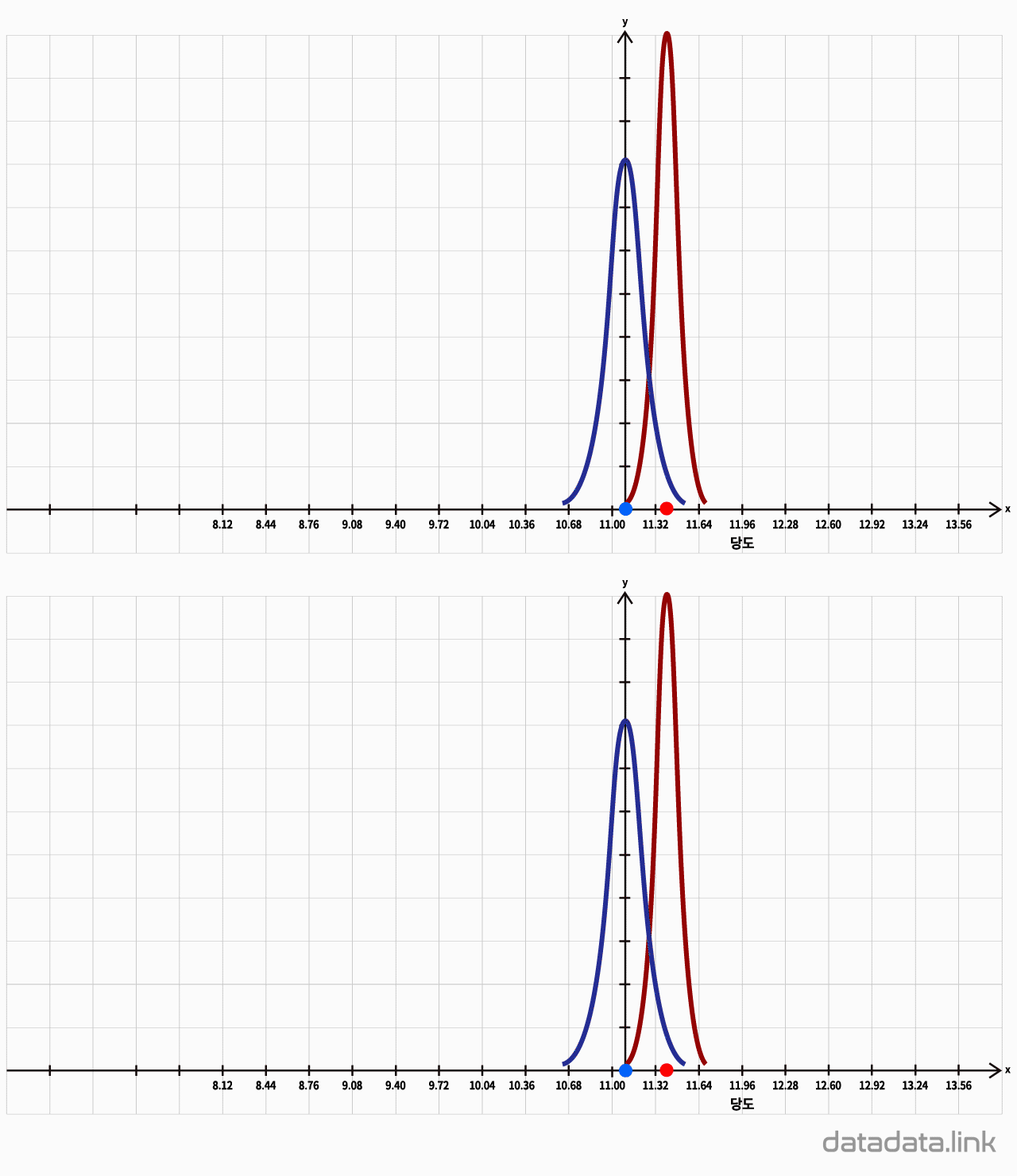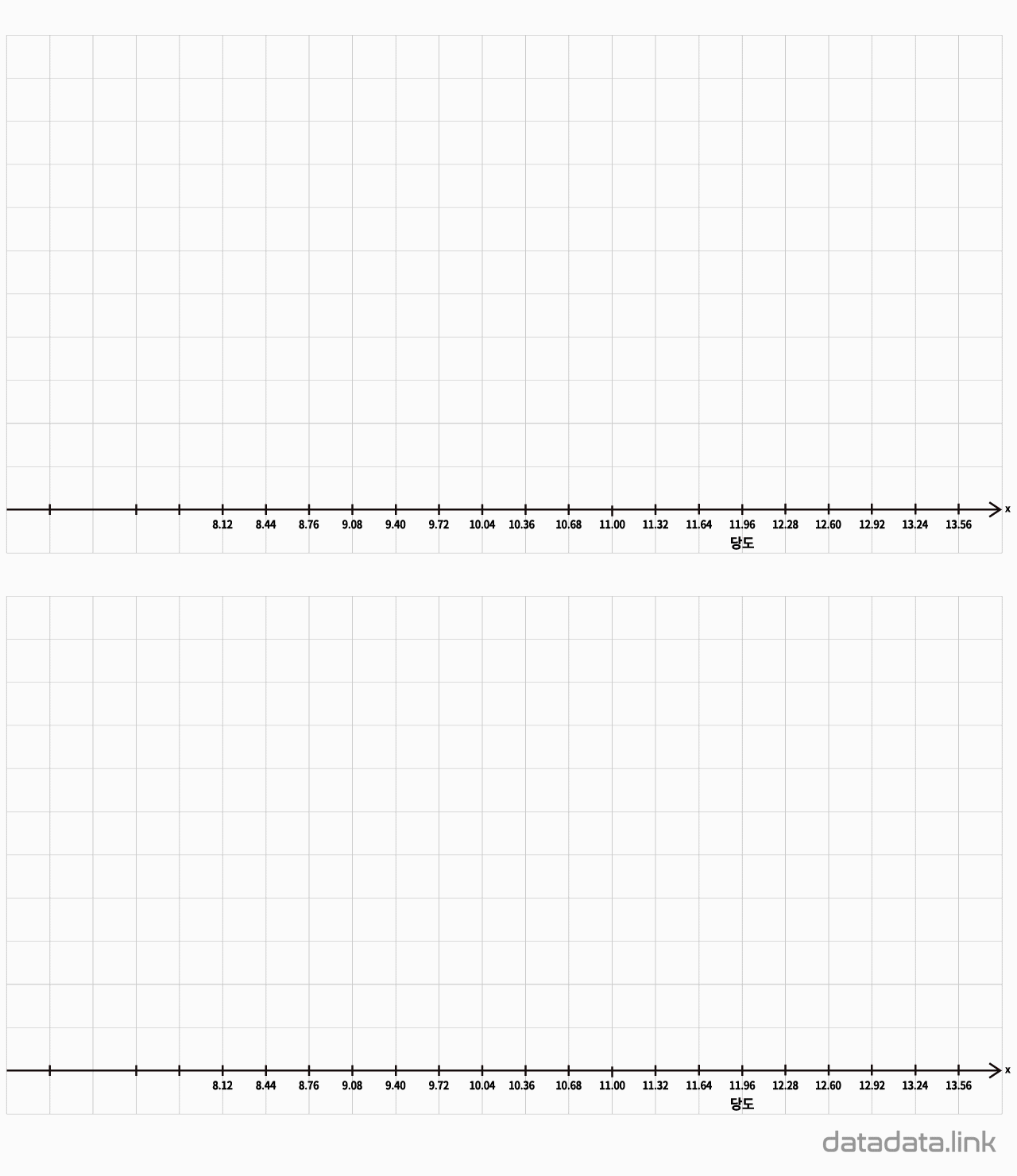
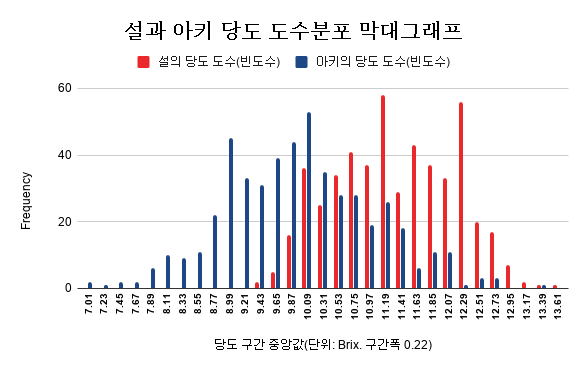
직관적으로 본다면 변수값들이 평균을 중심으로 멀리 흩어져 있으면 분산의 값이 커집니다.

그리고, 변수값(데이터값)이 평균 주위에 몰려 있으면 분산의 값이 작아 진다고 볼 수 있습니다.

모집단의 분산을 모분산(population variance)이라 부르며, 표본의 분산을 표본분산(sample variance)이라 부릅니다.

모분산과 표본분산의 수식은 차이가 있습니다.

표본분산을 계산할 때(데이터값과 평균과의 거리제곱의 평균을 구할때)는 표본의 크기인  n대신 1을 뺀  n-1을 사용합니다.

그 이유는 표본분산은 모집단에서 주어진 기준이 아닌 표본 내에서 만들어진 표본평균을 기준으로 하기 때문에, 이를 보정하기 위해 n 대신 n-1을 사용합니다.

표본의 크기(데이터의 갯수)가 작으면 표본분산을 구할 때 n(표본의 크기)과 n-1의 차이는 크게 나타납니다.

다른 표현으로는 표본에서 각 데이터의 거리가 나타나는 경우의 수는 데이터의 갯수 n에서 1을 뺀 수가 된다고 볼 수 있습니다.

분산은 평균값에서 각 변수값까지의 거리를 제곱한 후 그 평균을 구한 것이라는 것을 볼 때 n-1과 n의 차이는 더 큽니다.

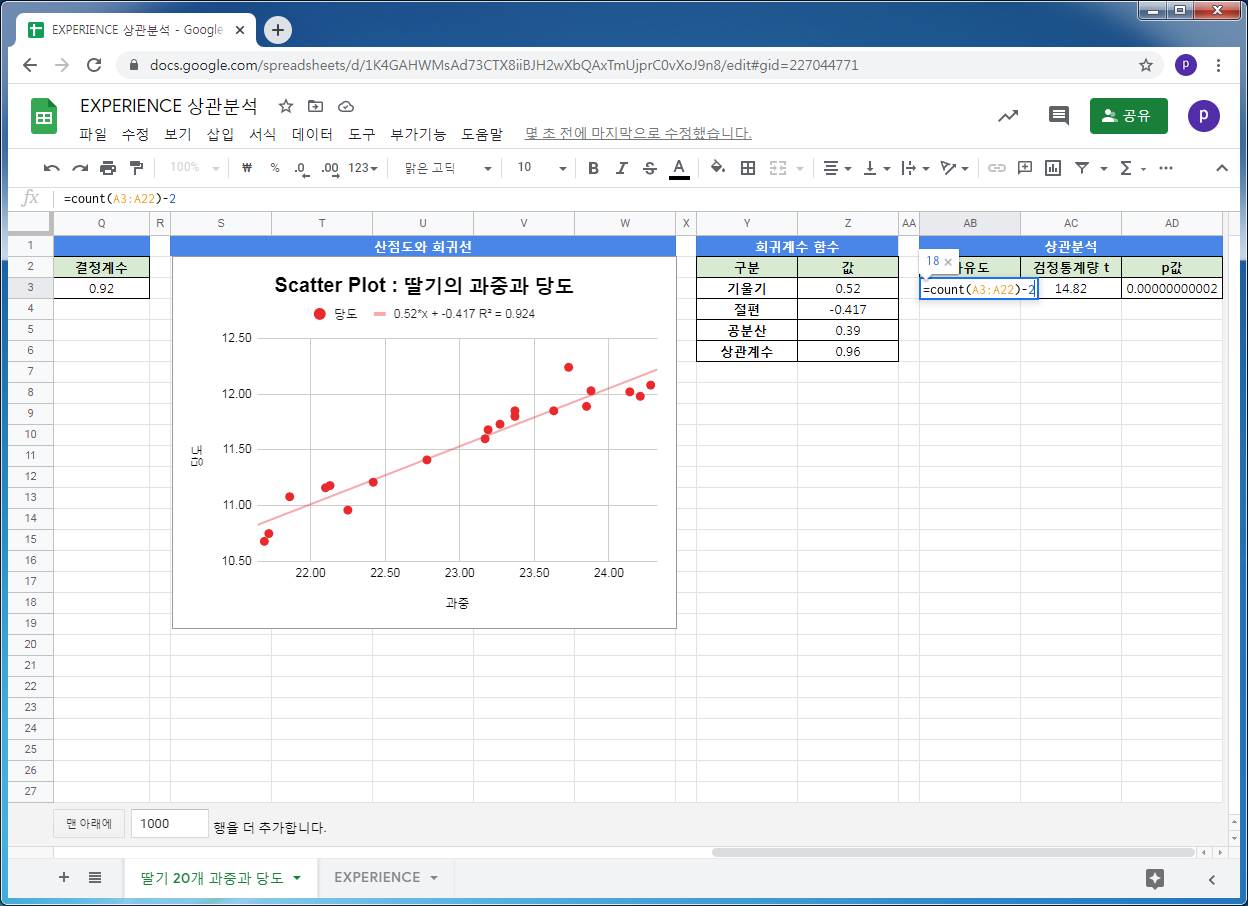
표준편차(standard deviation)는 분산의 제곱근으로 정의합니다.

따라서 분산이 구해지면 표준편차는 자동적으로 구해집니다.

표준편차는 데이터와 단위가 같게 되어 값이 실제값을 나타냅니다.

모집단의 표준편차를 모표준편차라고 부르며 $\sigma$로 표시합니다.

표본의 표준편차를 표본표준편차라고 부르며 $S$로 표시합니다.

분산은 제곱거리의 평균이어서 현실감을 느끼기가 힘드나 표준편차는 평균이나 변수값과 같은 단위가 되기 때문에 실감할 수 있습니다.

만약 두 개 이상의 표본의 표준편차를 비교할 때에는 표준편차를 평균으로 나눈 변동계수(coefficient of variation, 변이계수)를 사용합니다.

평균으로 표준화된 표준편차인 변동계수를 사용하면 분자 분모의 단위가 없어지고 표준화되어 두 표본의 변동 비교가 쉬워집니다.