개체분포
Individual distribution
1. 애니메이션
2. 설명
2.1. 개체와 도수
개체(object)
개체는 속성을 가집니다. 개체(예를 들면 인간)의 속성은 실현되기 전에는 알 수 없는 속성(예를 들면 성별)과 관측하기 전에는 알 수 없는 속성(예를 들면 사는 곳, 몸무게)이 있습니다. 실현되기 전과 관측하기 전의 개체의 속성을 변수로 모델링하는 데 특별히 확률값을 가지는 확률변수로 모델링할 수 있습니다. 그리고 개체가 가지는 속성을 모델링한 확률변수의 확률분포는 속성을 관측함으로써 특정 범주 또는 집단에서의 통계적 확률분포를 구할 수 있습니다.
예를 들어 한우를 개체로 볼 때 개체의 속성으로 품질등급이 있습니다. 각 품질등급에 속하는 한우의 수로 한우품질의 분포를 볼 수 있습니다. 그리고 한우가 속하는 범주별(예를 들면 생산지별)로 한우품질의 분포도 볼 수 있습니다. 이 때 관측한 한우의 개체수가 커질수록 관측하여 구한 한우품질의 분포는 한우품질의 속성을 표현한다고 볼 수 있습니다. 여기서 중요한 가정은 실현되기전 또는 관측하기전 각 개체의 속성의 확률분포는 같다는 것입니다.
6면 주사위를 개체로 보고 속성의 실현을 주사위를 던진 후 나타난 윗면이라고 모델링합니다. 이 때 속성을 나타내는 변수값은 여섯개의 각면이 됩니다.각 면에 1, 2, 3, 4, 5, 6의 여섯개 숫자를 쓰고 변수명을 “주사위를 던져서 나온 수”라고 더 자세히 모델링할 수 있습니다. 만일 주사위를 완벽한 정육면체로 가정한다면 각 확률변수값이 가지는 확률값은 모두 1/6이며 확률분포는 이산형 균등분포라고 할 수 있습니다. 여기서 중요한 점은 개체의 속성은 관측할 때 실현되는 확률변수로 모델링한다는 점입니다. 만일 한우품질이 여섯개의 등급으로 나타난다면 한우는 특정 모양의 6면 주사위를 가지는 속성을 가지고 생각할 수 있습니다. 이 때 속성의 실현과 관측은 주사위를 던지고 윗면을 기록하는 것과 같다고 할 수 있습니다.
확률변수는 범주형(질적)과 수치형(양적)으로 나누어 집니다. 개체의 속성을 관측한 값을 데이터 레코드(record)라 합니다. 개체의 ID와 데이터 레코드는 개체가 이루는 범주의 요소(element)라고도 합니다.
도수
도수(度数, frequency, 빈도수, 頻度数)는 빈도수의 약어입니다. 도수는 정해진 기간(period)에 정해진 공간(space)에서 개체(object)가 출현한 회수입니다. 개체의 속성을 표현하는 변수를 축(axis)으로 하는 좌표계로 공간을 표현합니다. 개체가 서로 독립적인 다수의 속성을 가진다면 개체를 다차원 공간에 출현한 점(point)으로 표현할 수 있습니다. 예를 들어, 개체가 서로 독립적인 3개의 속성을 가진다면 개체는 3차원 공간의 점(point)으로 볼 수 있습니다. 공간은 부분공간의 합으로 생각할 수 있고 부분공간의 위치는 부분공간을 대표하는 점(point)의 위치로 모델링할 수 있습니다. 정리하면, 전체공간을 이루는 각 부분공간에 개체가 정해진 시간동안 출현하는 회수가 그 부분공간의 도수가 됩니다.
개체분포의 도수분포화
개체의 분포를 도수의 분포로 만드는 방법은 개체가 속하는 범주(정해진 공간)로 개체를 구분하는 것으로부터 시작됩니다. 각 범주는 도수를 가지며 이 도수는 범주를 표현하는 “양(量)”이라고 할 수 있습니다. 따라서 도수분포는 “양(量)”으로 나타낸 범주의 분포라고 할 수 있습니다. 개체의 속성이 명목형이라고 하더라도 개체가 출현한 회수(도수)는 “양(量)”이므로 도수는 개체의 명목형 속성을 분석하고 예측하는 중요한 기반이 됩니다.
2.3. 개체분포(population distribution)의 시각화
개체는 개체가 가지는 속성이 만드는 공간에서 분포합니다. 따라서 개체분포를 시각화하기 위해서는 개체가 가지는 속성을 변수로 모델링한 좌표계를 우선 정합니다.
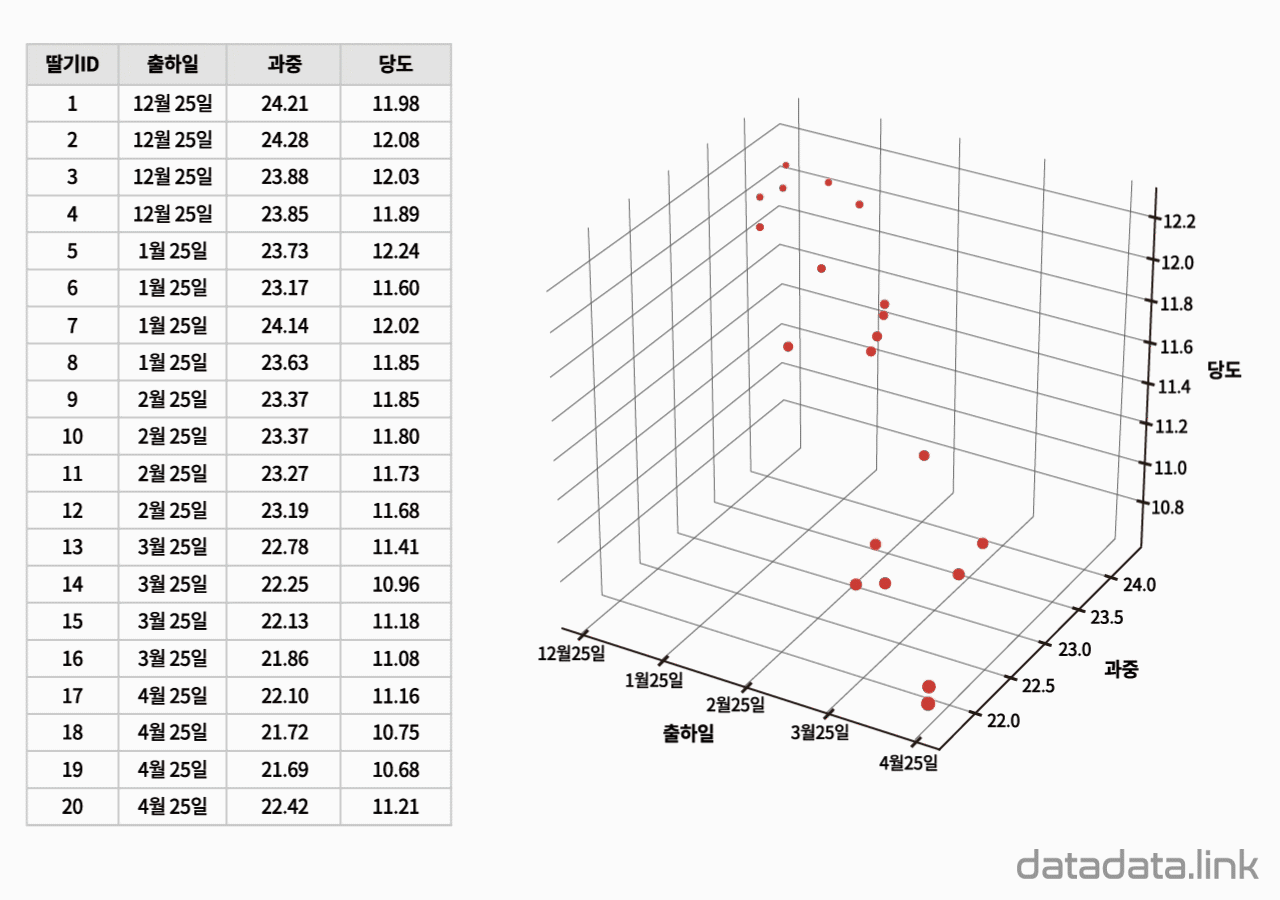
산점도(산포도, scatter plot)
산점도는 두 개 이상의 속성이 만드는 2차원 좌표계 또는 그 이상의 좌표계에서 개체의 분포를 시각화한 것입니다. 산점도는 개체의 속성이 만드는 공간에서 개체가 흩어진 모양을 관찰할 수 있으며 개체의 속성 간의 관계를 보여줍니다.
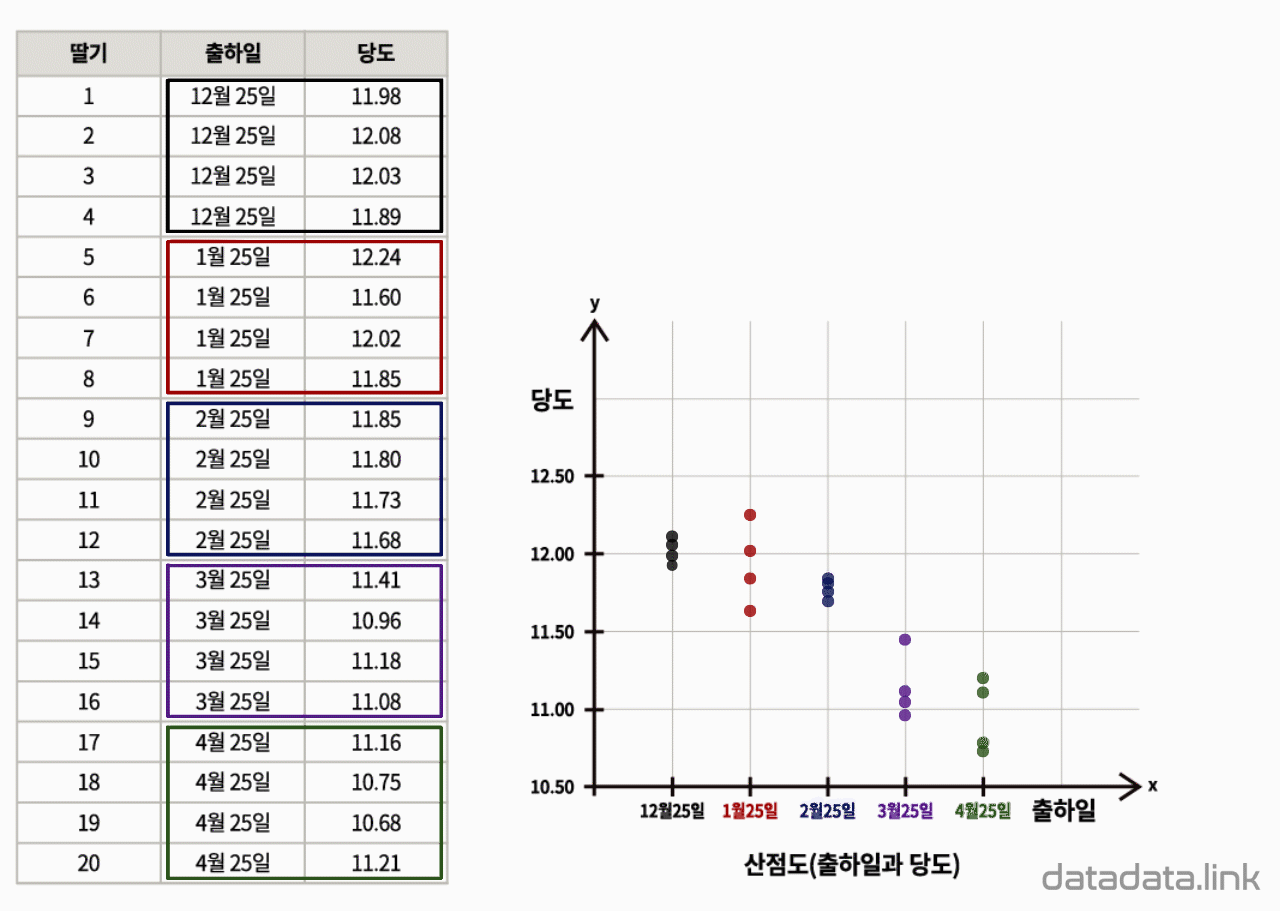
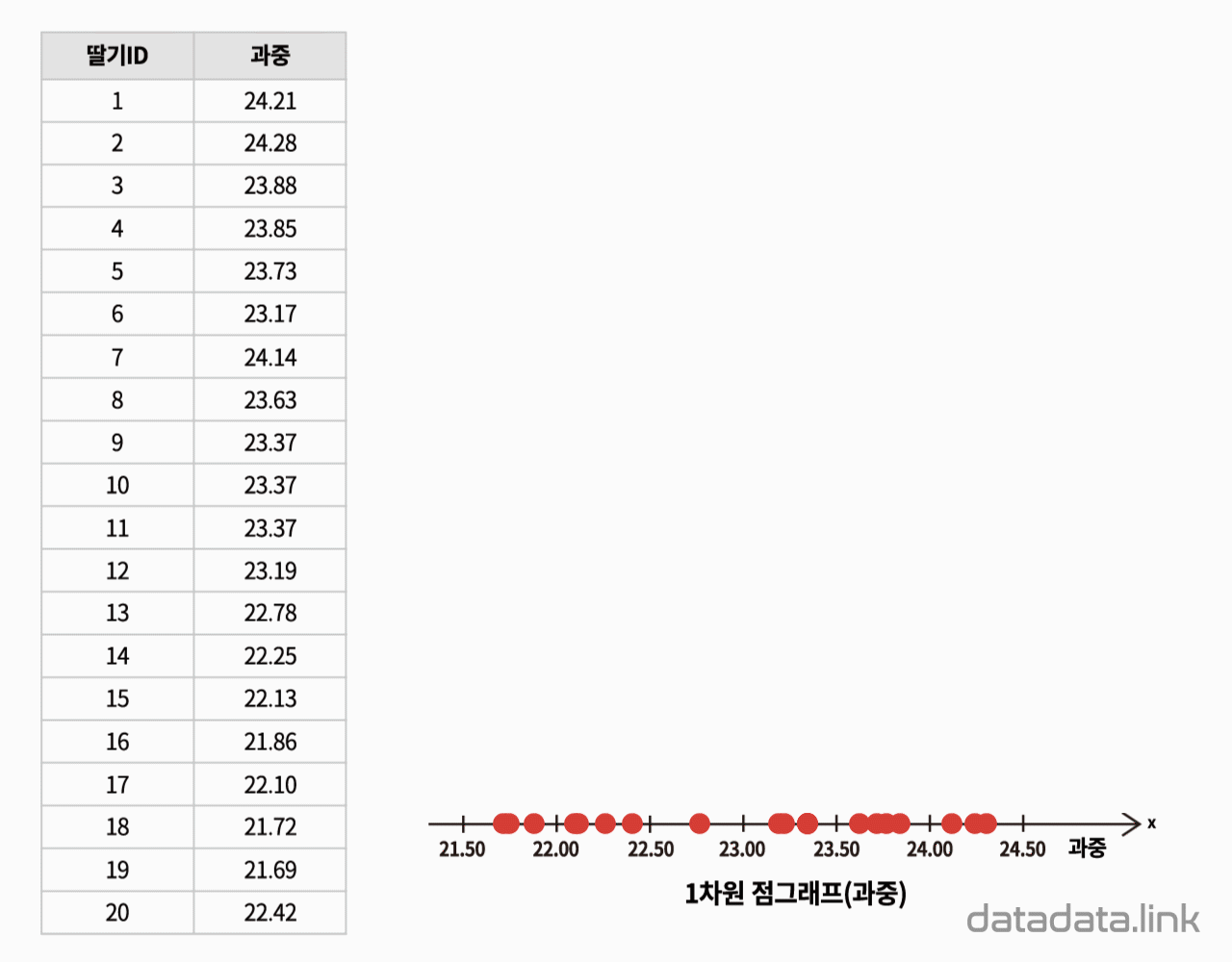
점그래프(dot plot)
점그래프는 개체의 속성이 하나인 경우 관측값을 1차원 좌표계에서 좌표축의 수직방향으로 겹치지 않게 점으로 쌓는 평면상의 그래프입니다. 점그래프는 관측값이 같은 경우라도 겹치지 않게 한 방향으로 쌓아 올리기 때문에 중심경향, 퍼짐정도, 특이값 등을 살펴볼 수 있습니다.
2.5. 개체분포의 모델
출현할 개체의 분포를 함수식으로 표현할 수 있으면 그 함수식을 개체분포의 모델이라고 합니다. 함수식으로 표현된 수학모델로 출현할 개체의 분포를 시각화할 수 있습니다. 개체분포의 모델은 개체의 확률분포와 같습니다.
이산형 확률분포 : 확률변수가 이산형
함수로 표현하는 대표적인 이산형 확률분포로는 베르누이분포, 이항분포, 포와송분포, 기하분포가 있습니다. 이 분포들의 정의역은 자연수(양의 정수)입니다. 그리고 함수값은 확률질량, 즉, 확률입니다. 그래서 이산형 확률분포를 나타내는 함수를 확률질량함수(probability mass function, PMF)라고 합니다.
연속형 확률분포 : 확률변수가 연속형
함수로 표현하는 대표적인 연속형 확률분포로는 정의역이 실수인 지수분포, 정규분포가 있고 정의역이 0에서 1인 베타분포가 있습니다. 감마분포는 정의역이 양의 실수입니다. 그리고 함수값은 확률밀도입니다. 그래서 연속형 확률분포를 나타내는 함수를 확률밀도함수(probability density function, PDF)라고 합니다. 함수값인 확률밀도를 적분하면 확률질량, 즉, 확률이 됩니다.
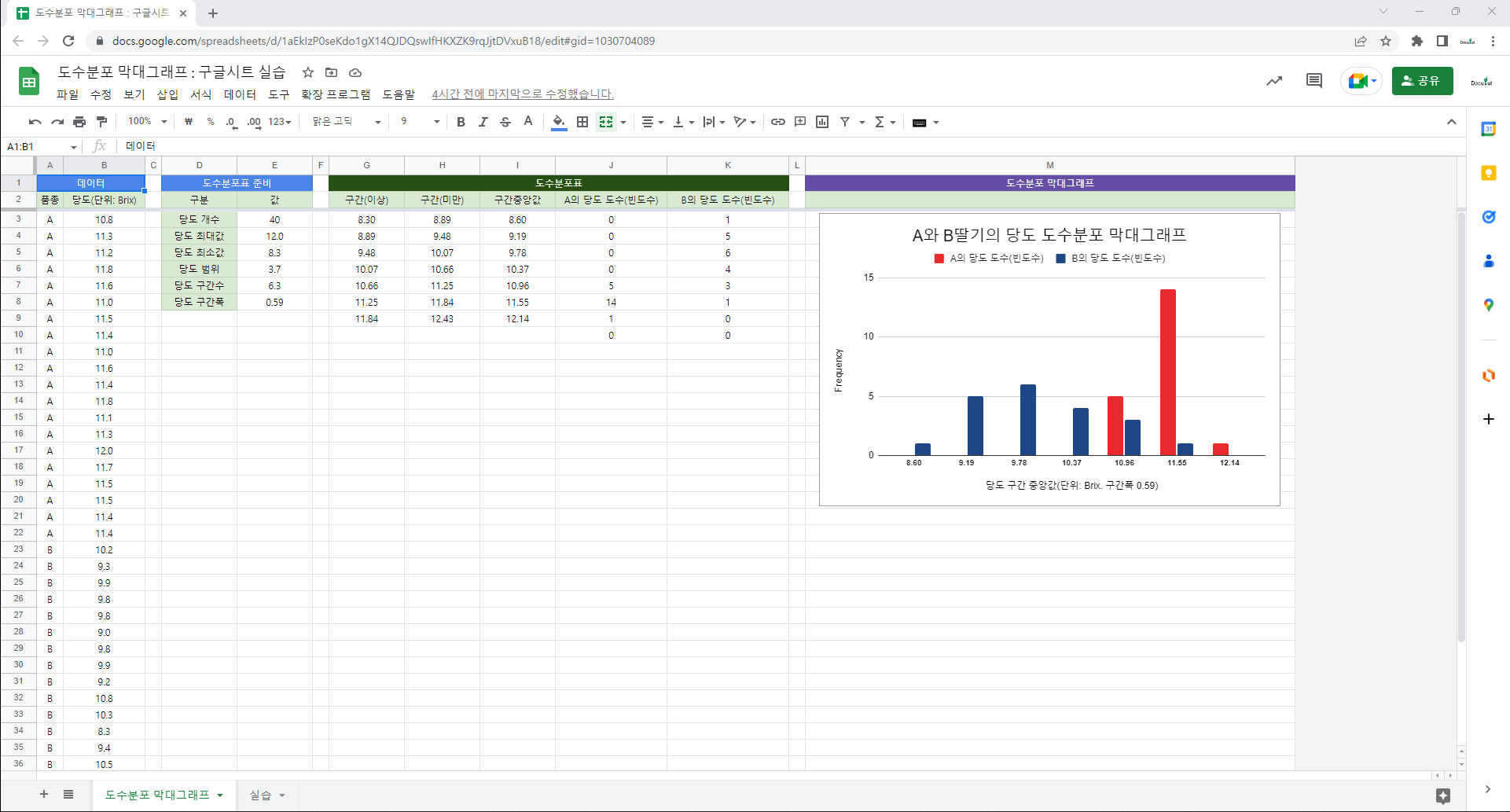
3. 실습
3.2. 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
3.3. 실습강의
– 데이터
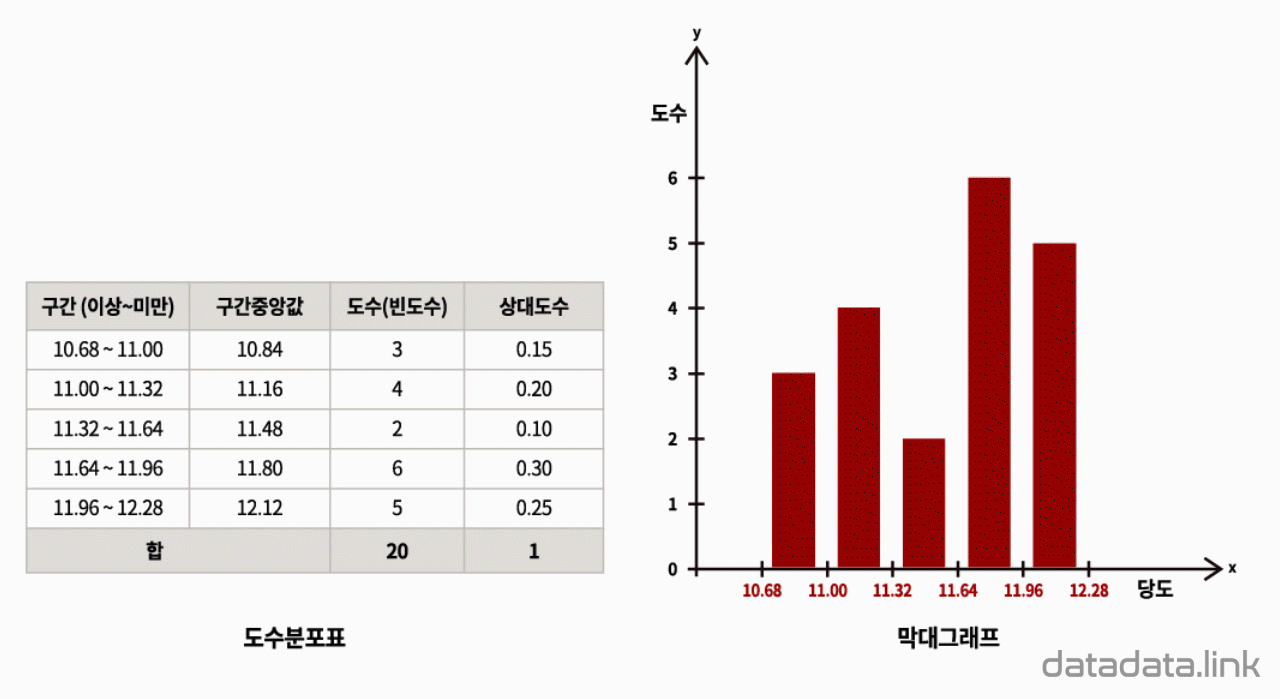
– 도수분포표
– 도수분포 막대그래프
4. 참조
4.1 용어
막대그래프
막대그래프는 데이터값에 비례하는 길이를 가지는 직사각형 막대로 데이터값을 표현합니다. 막대그래프는 세로 또는 가로로 그릴 수 있습니다. 세로 막대그래프는 때로는 선 그래프와 같이 표현됩니다. 막대그래프는 각 범주간 데이터값을 잘 비교합니다. 그래프의 한 축은 비교할 특정 범주를 표시하고 다른 축은 측정된 데이터값을 길이로 나타냅니다. 막대 그래프를 응용하면 두 개 이상의 그룹으로 묶어서 막대를 나타낼 수 있으며 둘 이상의 측정 변수의 값을 비교하여 보여 줄 수 있습니다.
Reference
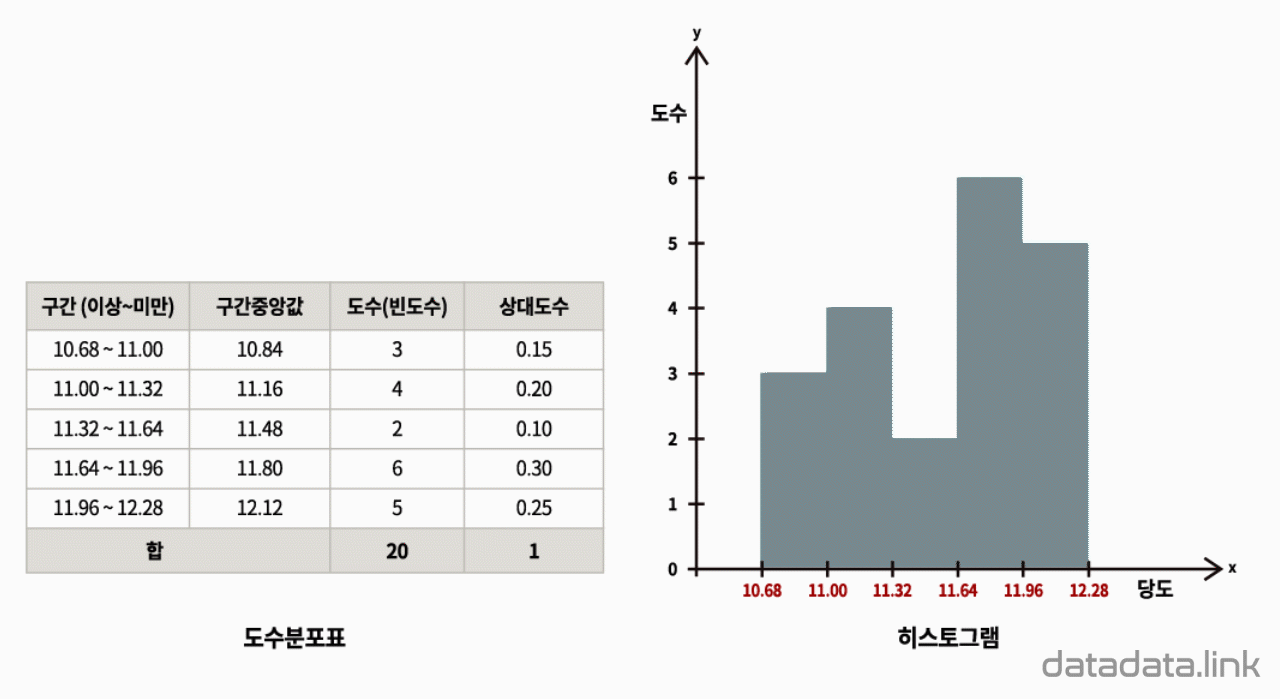
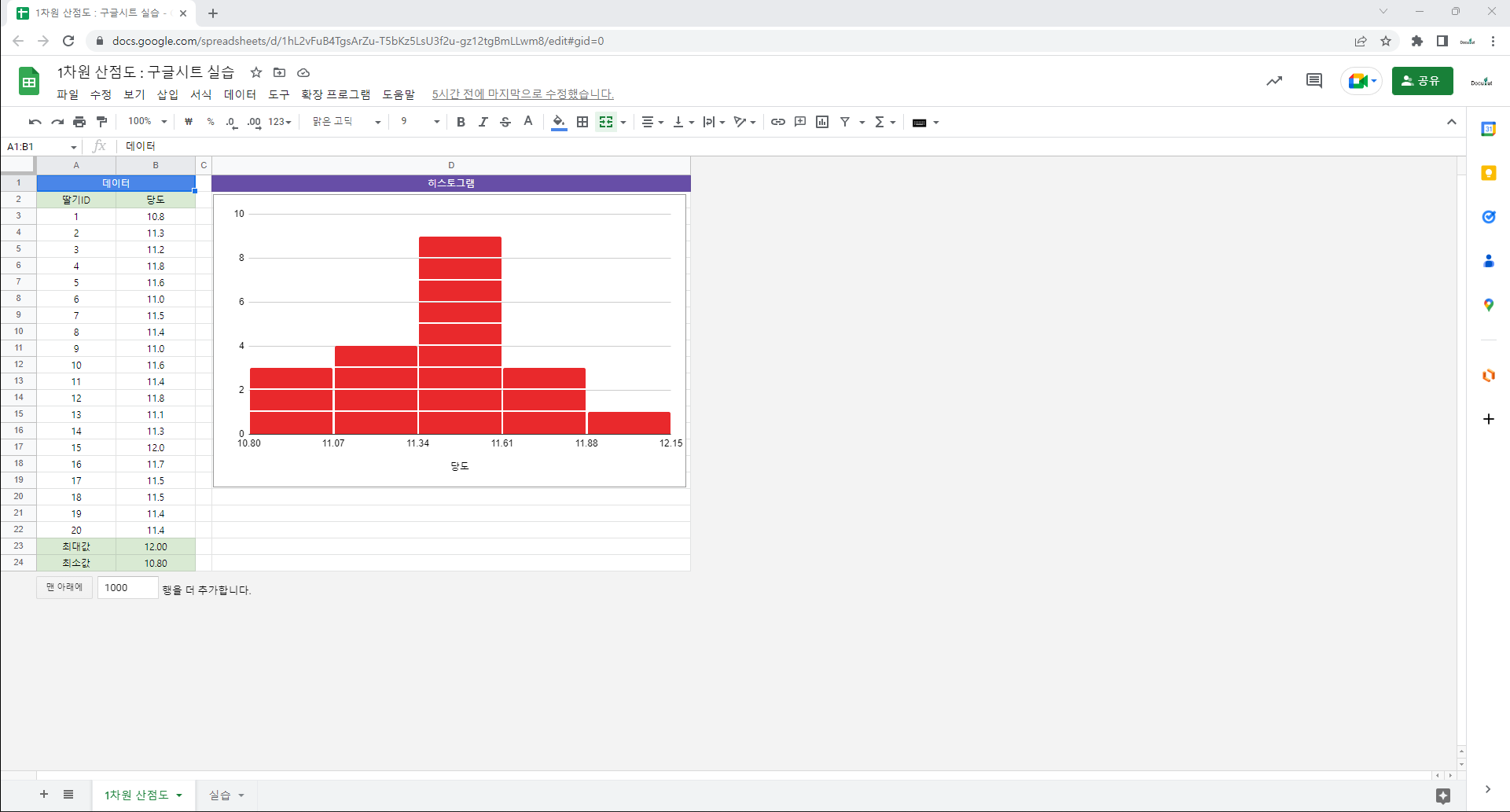
히스토그램
데이터값의 분포를 표현하는 방식중의 하나입니다. 연속확률변수의 확률값을 막대그래프 모양으로 표현한 것입니다. Karl Pearson에 의해 처음 소개되었습니다.
히스토그램을 작성하려면 먼저 변수 범위를 구간(“bin”또는 “bucket”)으로 나눕니다. 그리고 각 구간에 몇 개의 데이터 값이 속하는 지를 정리합니다. 구간은 연속적이고 겹치지 않고 인접해야 하며 같은 간격이면 분석에 용이합니다.(구간 간격이 꼭 같아야 하는 것은 아닙니다.)
직사각형(막대)의 높이에 비례하는 빈도수는 상대빈도수로 정규화될 수 있습니다. 구간들이 동일한 간격이고 간격이 1인 경우, 빈도수를 정규화하게 되면 각 직사각형의 높이는 상대빈도수를 표현하는 확률이 되어 각 직사각형의 높이의 합은 1이 됩니다. 그러나 구간은 동일한 폭(구간크기)일 필요는 없습니다. 이 경우 직사각형(막대)은 구간의 빈도수에 비례하는 면적을 갖도록 정의됩니다 . 수직축은 빈도수가 아니라 빈도수밀도(수평축상의 변수의 단위당 경우의 수)입니다. 모양은 막대 그래프의 막대가 서로 인접한 모양으로 변수가 연속적으로 표현되었다는 것이 중요합니다.
히스토그램은 데이터의 기본 확률분포밀도를 대략적으로 나타내며, 확률밀도 추정시 자주 사용됩니다 . 즉, 기본 확률변수의 확률밀도함수를 나타냅니다 . 확률 밀도에 사용되는 히스토그램의 총 면적은 항상 1로 정규화됩니다. $X$ 축의 간격이 모두 1이면 히스토그램은 상대빈도 막대그래프와 동일합니다 . 히스토그램은 통계적 속성을 모델링해야 할 때 통계 패키지 프로그램에서 자주 쓰입니다. 예를 들면, 커널 밀도 추정치의 상관 관계 변이는 수학적으로 설명하기가 매우 어렵지만 각 구간이 독립적으로 변하는 히스토그램에서는 이해하기가 쉽습니다. 커널 밀도 추정의 대안은 평균 이동된 히스토그램입니다 계산 속도는 빠르며 커널을 사용하지 않고 밀도를 부드럽게 계산할 수 있습니다.
히스토그램은 때때로 막대그래프와 혼동됩니다.히스토그램은 연속 데이터에 사용되기 때문에 막대는 붙어 있게 됩니다. 그래서 구별을 분명히 하기 위해 막대그래프는 막대 사이에 간격을 줍니다.
Reference
4.2. 참고문헌