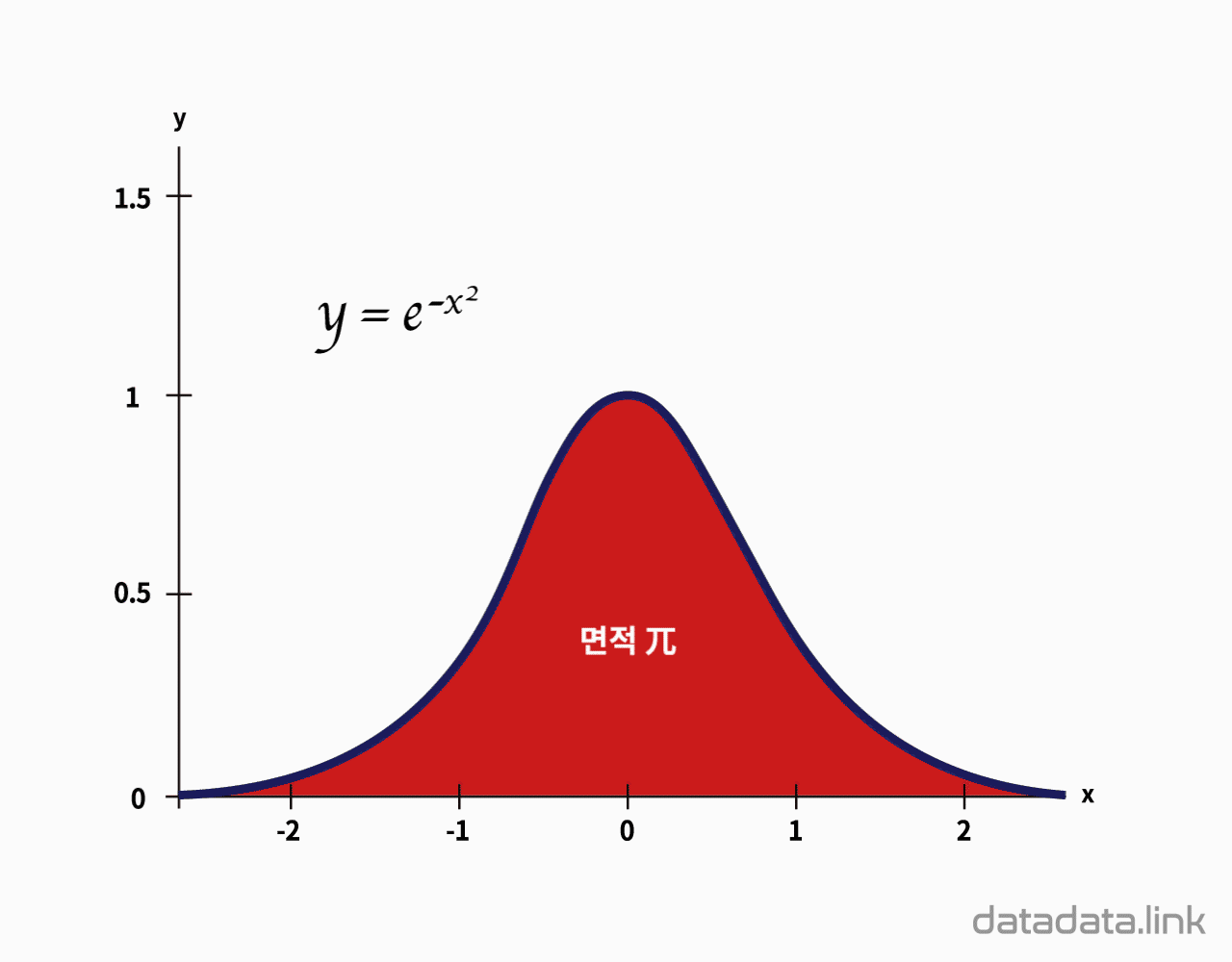
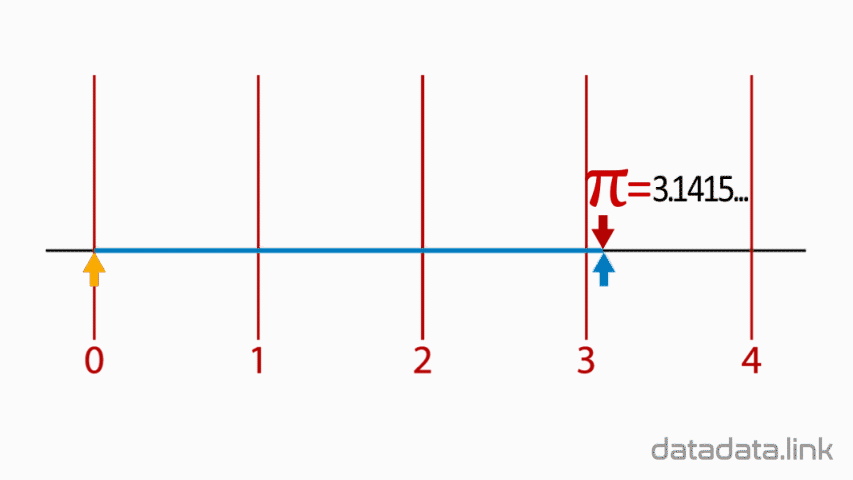
척도와 단위
Scale & unit
1.1. 수체계
1. 애니메이션
2. 설명
2.1. 물리에서 사용하는 척도와 단위
물리적인 양을 측정할 때, 관측도구를 사용합니다. 관측도구에는 척도(scale)와 단위(unit)가 적용됩니다. 척도는 특정한 속성을 측정하기 위해 사용합니다. 척도에 따르는 단위는 측정의 기본적인 ‘양(quantity)’을 나타냅니다. 단위는 보통 국제적으로 표준화되어 있습니다. 예를 들어, 온도를 측정할 때 ‘도(°)’는 단위이며, 섭씨나 화씨는 이 온도를 표현하는 척도입니다.
기본 물리량의 척도와 단위
|
물리량 physical quantities |
척도(단위) scale(unit) |
국제 단위계 SI |
척도유형 scale type |
| 길이 | 미터(m), 센티미터(cm), 킬로미터(km), 마일(miles), 인치(inches) | m | 비율척도 |
| 질량 | 킬로그램(kg), 그램(g), 파운드(lbs), 온스(oz) | kg | 비율척도 |
| 시간 | 초(s), 분(min), 시(hour), 일(day), 년(year) | s | 비율척도 |
| 전류 | 볼트(V), 암페어(A), 와트(W), 옴(Ω) | A | 비율척도 |
| 온도 | 켈빈(K), 섭씨(°C), 화씨(°F) | K | 비율척도 |
| 물질의 양 | 몰(mol) | mol | 비율척도 |
| 광도 |
칸델라(cd) |
cd | 비율척도 |
주요 물리량의 보편적인 척도와 단위
|
물리량 physical quantities |
척도(단위) scale |
척도유형 scale type |
| 지진의 강도 | 리히터규모(단위없음) | 순서척도 |
| 산성도 | pH(단위없음) | 로그척도(logarithm scale) |
| 소리의 크기 | 데시벨(dB) | 로그척도(logarithm scale) |
2.2. 경제에서 사용하는 척도와 단위
경제에서 나타나는 개념을 양으로 표현할 때 그 양을 표현하기 위해 척도와 그에 따른 단위를 사용합니다.
경제에서의 주요 척도와 단위
|
경제량 economic quantities |
척도(단위) scale(unit) |
척도유형 scale type |
| 통화 | 한국 원(KRW), 미국 달러(USD), 유로(EUR), 일본 엔(JPY) 등 | 비율척도 |
| 성장률 | 경제 성장률(%), 인구 성장률(%) | 비율척도 |
| 지수 | 주가지수(단위없음), 물가지수(단위없음) | 간격척도 |
3. 실습
3.2. 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
3.3. 실습강의
– 실습강의 목차

4. 참조
4.1 용어
리커트 척도
리커트 척도는 그 발명자인 미국의 사회심리학자 Rensis Likert의 이름을 딴 심리측정 척도입니다. 이 척도는 연구 설문지에서 흔히 사용됩니다. 설문 연구에서 응답을 척도화하는 방식으로 가장 널리 사용되며, 때문에 ‘리커트 유형 척도(Likert-type scale)’라는 용어는 평가 척도(rating scale)와 종종 동의어로 사용되기도 하지만, 평가 척도에는 다른 유형들도 있습니다.
리커트는 척도 자체와 응답이 점수화되는 형식 사이를 구분하였습니다. 엄밀히 말하면, 리커트 척도는 전자만을 가리킵니다. 이 두 개념 사이의 차이는 리커트가 조사하려는 기본 현상과 그 현상을 나타내는 변동을 포착하는 방법 사이의 구분에서 나옵니다.
리커트 항목에 응답할 때, 응답자들은 일련의 진술에 대한 동의 또는 불일치의 수준을 대칭적인 동의-불일치 척도에서 지정합니다. 따라서, 척도는 주어진 항목에 대한 그들의 감정의 강도를 포착합니다.
척도는 개별 항목(질문) 세트에 대한 설문지 응답의 단순한 합계나 평균으로 생성될 수 있습니다. 이렇게 하면, 리커트 척도는 각 선택 사이의 거리가 동일하다고 가정합니다. 많은 연구자들은 높은 내적 일관성을 보이는 항목 세트를 사용하며, 동시에 연구 대상 전체 영역을 포착할 것이라고 가정합니다. 다른 연구자들은 “모든 항목이 서로의 복제본이라고 가정하거나 다시 말해 항목들이 병렬 도구로 간주된다”는 기준을 고수합니다. 반면, 현대의 시험 이론은 각 항목의 난이도를 항목 척도화에 포함시킬 정보로 간주합니다.
리커트 척도의 등간성에 대한 논의는 연구자들 사이에서 여전히 진행 중인 토론의 주제입니다. 일부 연구자들은 리커트 척도를 등간척도로 간주하여 적절한 통계 분석을 수행하며, 다른 연구자들은 그렇지 않다고 주장합니다.
특히 리커트 척도의 등간성을 수학적으로 증명한 구체적인 참고문헌을 제공하기는 어렵습니다. 이는 대부분의 연구가 통계적 또는 실증적인 근거를 기반으로 하는데, 수학적 증명 방식과는 다르기 때문입니다. 리커트 척도의 성질과 사용에 대한 더 깊은 연구나 이해를 원한다면, 측정 이론 (measurement theory) 또는 척도 이론 (scale theory) 관련 문헌을 참조하는 것이 좋습니다.