확률변수의 독립
1.1. 사건$H$와 사건$E$가 독립일 때 곱사건의 확률
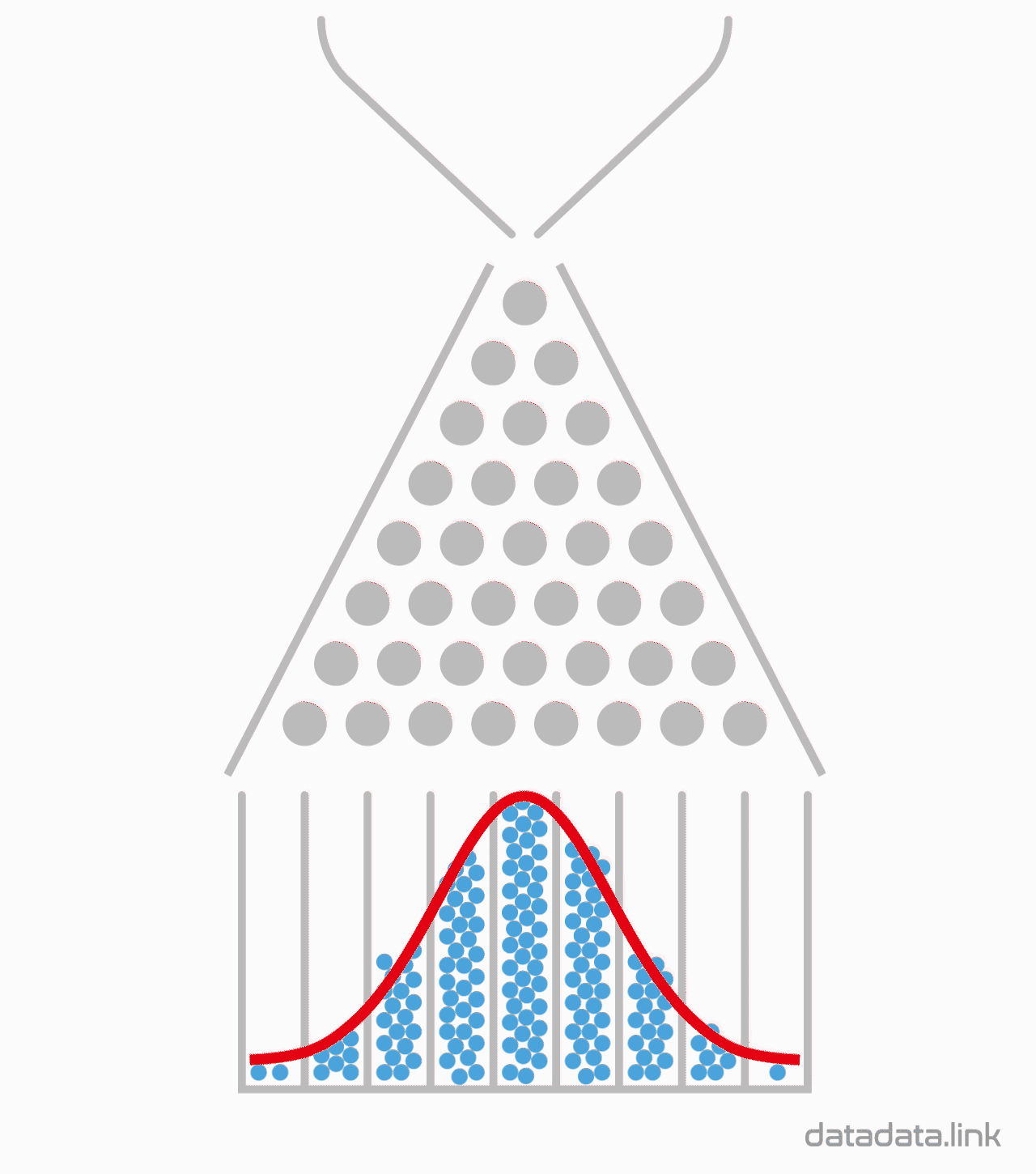
1. 애니메이션
2. 설명
2.1. 확률변수의 독립
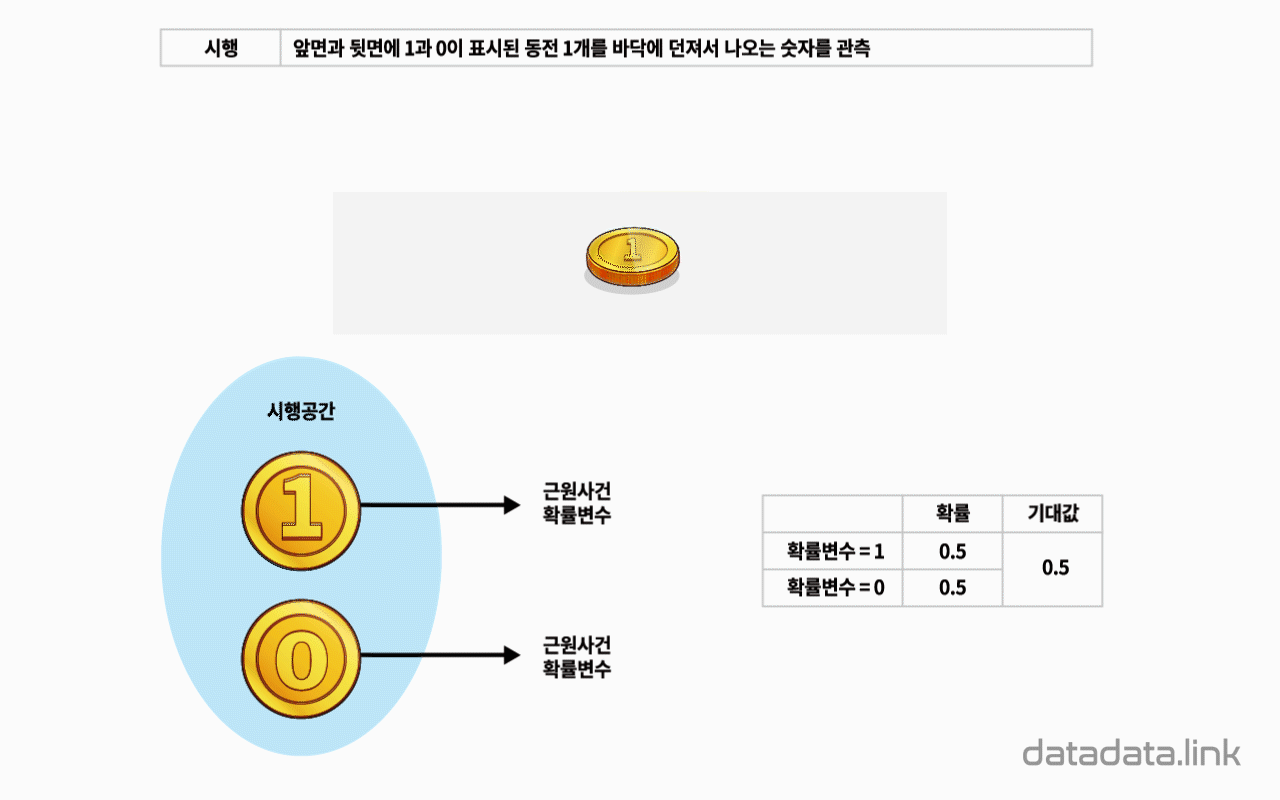
두 확률변수 $X$와 $Y$의 독립
사건 A와 사건 B가 독립이면 곱사건의 확률 $P(A \cap B)$은 조건부확률계산을 할 필요가 없이 두 사건의 확률을 곱하여 구할 수 있습니다.
$P(A \cap B)=P(A)P(B)$
두 확률변수 $X$와 $Y$가 독립이면 곱사건의 확률은 다음식과 같습니다.
$$f(x,y)=g(x)h(y)$$
여러 확률변수간 서로 독립
여러 확률변수가 상호 독립임을 안다면 곱사건의 확률은 각 사건의 확률의 곱으로 나타납니다. 확률변수 $X1,X2,\cdots,Xn$가 서로 독립이면 다음식이 성립합니다.
$$f(x_1,x_2,\cdots,x_n)=f(x_1)f(x_2)\cdots f(x_n)$$
모두 이산형 확률변수인 경우는 다음과 같이 확률식을 표현할 수 있습니다.
$$P(X_1,X_2,\cdots,X_n)=P(X_1)P(X_2)\cdots P(X_n)$$
2.2. 두 확률변수간 독립 판별
모두 이산형 확률변수인 경우는 결합확률질량함수를 각각의 주변확률질량함수의 곱과 비교하여 같으면 독립입니다.
모두 연속형 확률변수인 경우는 결합확률밀도함수를 각각의 주변확률밀도함수의 곱과 비교하여 같으면 독립입니다.
두 확률변수 $X$와 $Y$의 독립의 성질을 이용하여 독립 판별
성질 1
$${\rm E}[XY]=\mu_X\mu_Y$$
증명
$$\begin{align}
{\rm E}[XY] & = \int\int xyg(x)h(y)dxdy \\
& = \int xg(x)dx \int yh(y)dy \\
& = {\rm E}[X]{\rm E}[Y] \\
& = \mu_X\mu_Y \\
\end{align}$$
성질 2
확률변수 $X$와 $Y$가 독립이면 공분산은 0이 됩니다.
$${\rm Cov}(X,Y)=0$$
${\rm Cov}(X,Y)=0$이라고 해도 확률변수 $X$와 $Y$가 독립이라고 할 수 없습니다. $Cov(X,Y)=0$일 때 확률변수 $X$와 $Y$의 독립 판별은 모든 $x$, $y$에 대해 $f(x,y)=g(x)h(y)$ 인지 확인해야 합니다.
성질 3
확률변수 $X$와 $Y$가 독립이면 두 확률변수 합의 분산은 다음과 같습니다.
$${\rm Var}[X \pm Y]={\rm Var}[X]+{\rm Var}[Y]$$
여기서, 확률변수 $X$와 $Y$가 독립이면 ${\rm Cov}(X, Y)=0$
2.3. 두 확률변수의 선형결합
독립인 두 확률변수, $X$와 $Y$의 선형결합은 다음식으로 표현할 수 있습니다.
$$U=aX+bY$$
기대값의 식은
$${\rm E}[𝑈]=𝑎{\rm E}[𝑋]+𝑏{\rm E}[𝑌]$$
분산의 식은
$${\rm Var}[𝑈]=𝑎^2 {\rm Var}[𝑋]+𝑏^2{\rm Var}[𝑌]+2𝑎𝑏{\rm Cov}(𝑋,𝑌)$$
여기서, 확률변수 $X$와 $Y$가 독립이면 ${\rm Cov}(X,Y)=0$
$𝑋=𝑋_1+𝑋_2+\cdots+𝑋_𝑛$이며, $𝑋_1,𝑋_2,\cdots,𝑋_𝑛$가 서로 독립이라면 기대값의 식은
$${\rm E}[X]={\rm E}[X_1]+{\rm E}[X_2]+\cdots+{\rm E}[X_n]$$
$𝑋=𝑋_1+𝑋_2+\cdots+𝑋_𝑛$이며, $𝑋_1,𝑋_2,\cdots,𝑋_𝑛$가 서로 독립이라면 분산의 식은
$${\rm Var}[X]={\rm Var}[X_1]+{\rm Var}[X_2]+\cdots+{\rm Var}[X_n]$$
$𝑋=𝑋_1+𝑋_2+\cdots+𝑋_𝑛$이며, $𝑋_1,𝑋_2,\cdots,𝑋_𝑛$가 서로 독립이라면 공분산의 식은
$${\rm Cov}(X_i, X_j)=0$$
2.4. 두 확률변수의 상관계수
상관계수(correlation coefficient)는 두 연속형 변수의 선형관계를 나타내는 것 이외에 확률변수 $X$의 증감에 따른 확률변수 $Y$의 증감 정도를 나타내는 측도로도 사용할 수 있습니다. 그리고 상관계수는 두 확률변수의 선형결합에서의 계수비이므로 두 확률변수의 단위가 소거됩니다. 따라서 상관계수는 단위에 민감한 공분산의 문제점을 해결할 수 있습니다. 피어슨 상관계수는 다음과 같습니다.
$$\rho_{X,Y}=\dfrac{{\rm Cov}(X,Y)}{\sqrt{{\rm Var} [X]}\sqrt{{\rm Var}[Y]}}$$
여기서, $-1 \leq \rho_{X,Y} \leq 1$
$\rho_{X,Y}$는 단위가 없는 값
상관계수는 ${\rm Cov}(X,Y)$를 각각의 표준편차인$\sqrt{{\rm Var}[X]}$와 $\sqrt{{\rm Var}[X]}$로 나눈 값입니다. 따라서 -1과 1 사이의 값을 가지고 단위에 민감한 공분산과 달리 단위가 없습니다. $\rho_{(X,Y)}$가 각각 1과 -1인 경우는 $ X$와 $Y$가 완벽한 상관을 이루는 경우입니다. 나머지 영역은 상관은 다음과 같이 분류할 수 있습니다.
정비례상관
$$0 \lt \rho_{(X,Y)} \lt 1$$
무상관
무상관은 서로 정보에 대해서 아무런 공유가 없다는 의미입니다.
$$\rho_{(X,Y)}=0$$
반비례상관
$$−1 \lt \rho_{(X,Y)} \lt 0$$
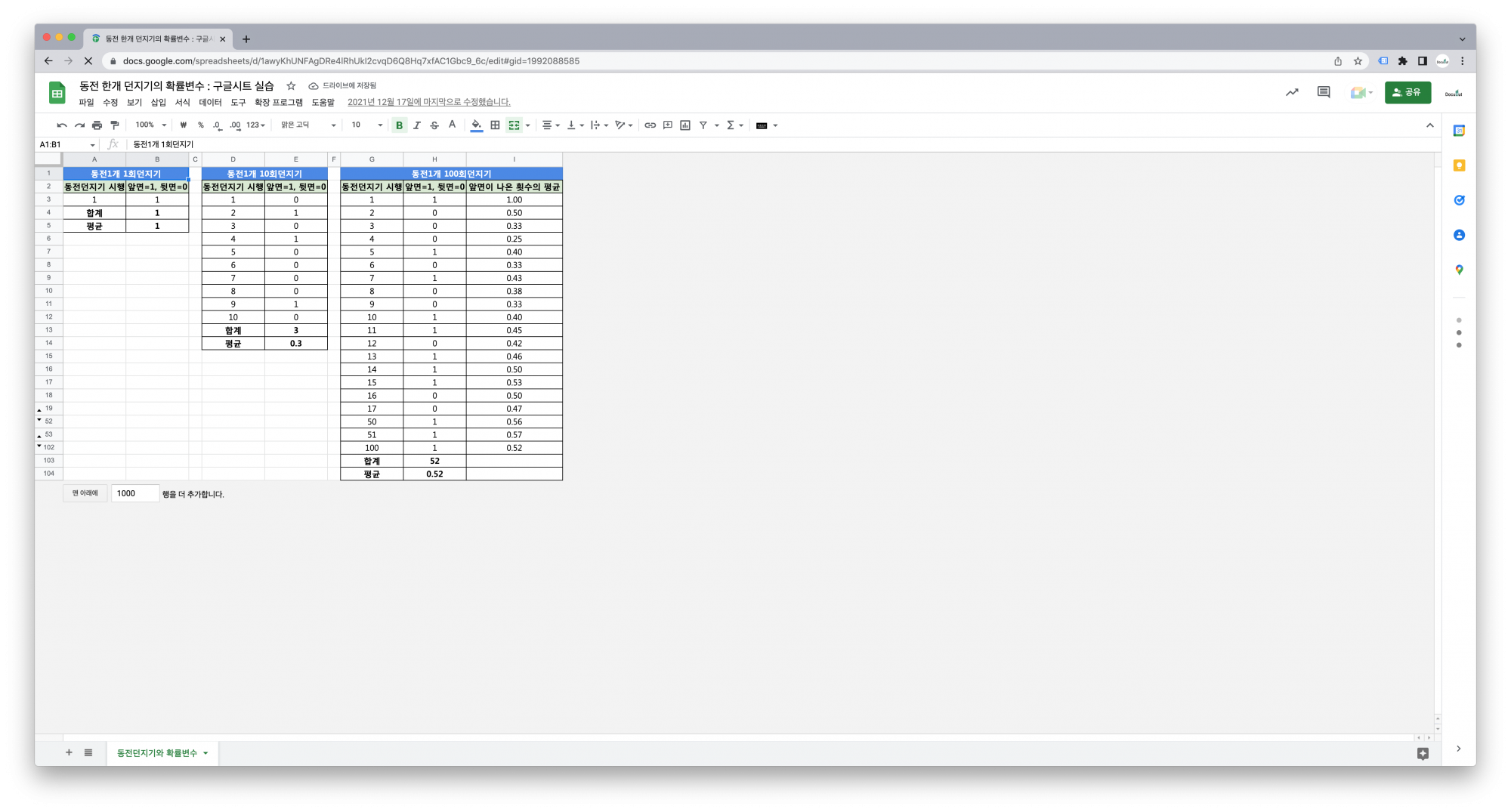
3. 실습
3.2. 함수
=ROWS(F2:F2) : 지정된 배열 또는 범위에 있는 행의 개수.
3.3. 실습강의
– 실습강의 목차

4. 참조
4.1 용어
확률변수
확률이론 및 통계에서 임의의 양, 임의의 변수, 즉 확률변수는 비공식적으로 값이 임의의 현상의 결과에 의존하는 변수로 설명됩니다. 확률변수에 대한 공식적인 수학적 설명은 확률이론의 주제입니다. 그 맥락에서, 확률변수는 결과가 일반적으로 실수인 확률공간에서 정의된 측정 가능한 함수로 이해할 수 있습니다.
확률변수의 가능한 값은 아직 수행되지 않은 실험의 가능한 결과 또는 이미 존재하는 값 불확실한 과거 실험의 가능한 결과인 경우를 나타내는 이미 존재하는 값으로 나타낼 수 있습니다 (예 : 부정확한 측정 또는 양자 불확실성으로 인해). 그들은 또한 개념적으로 “객관적”무작위 과정의 결과 또는 양에 대한 불완전한 지식으로 인한 “주관적인”무작위성”을 나타낼 수 있습니다. 확률변수의 잠재 가치에 할당된 확률의 의미는 확률 이론 자체의 일부가 아니며 확률의 해석에 대한 철학적 주장과 관련이 있습니다. 수학은 사용되는 특정 해석과 상관없이 동일하게 작동합니다.
함수로서 확률변수는 측정 가능해야 하며 확률은 잠재가치 집합으로 표현할 수 있습니다. 결과는 예측할 수 없는 몇 가지 물리적 변수에 달려 있을 수 있습니다. 예를 들어, 공정한 동전 던지기의 경우, 앞면 또는 뒷면의 최종 결과는 불확실한 동전의 물리적 조건에 달려 있습니다. 관찰되는 결과는 확실하지 않습니다. 동전의 표면에 균열이 생길 수 있지만 이러한 가능성은 고려 대상에서 제외됩니다.
확률변수의 존재 지역은 표본공간이며 임의의 현상의 가능한 결과의 집합으로 해석됩니다. 예를 들어, 동전 던지기의 경우 두 가지 가능한 결과, 즉 앞면 또는 뒷면이 그러합니다.
확률변수는 확률분포를 가지며, 확률분포는 확률변수의 확률값을 지정합니다. 무작위 변수는 이산형일 수 있습니다. 즉, 임의의 변수의 확률분포의 확률 질량함수 특성이 부여된 유한한 값 또는 계산 가능한 값에서 하나를 취합니다. 또는 임의의 변수의 확률분포의 특징 인 확률밀도함수를 통해 간격 또는 연속된간격에서 임의의 수치 값을 취하는 연속 또는 두 유형의 혼합물 일 수 있습니다.
동일한 확률분포를 갖는 두 개의 확률 변수는 다른 확률 변수와의 관련성 또는 독립성 측면에서 다를 수 있습니다. 무작위 변수의 실현, 즉 변수의 확률분포 함수에 따라 무작위로 값을 선택한 결과를 무작위 변수라고 합니다.
Reference
연속, 불연속 변수
수학에서 변수는 연속이거나 이산일 수 있습니다. 두 개의 특정 실제 값 (예 : 임의의 가까운 값) 사이의 모든 실제 값을 취할 수 있는 경우 변수는 해당 간격에서 연속입니다. 변수가 가질 수 있는 값을 포함하지 않는 극한의 간격이 양측에 존재하는 값을 취할 수 있다면, 그 변수값을 중심으로 변수는 분리되고 그 변수는 이산형 변수입니다. 일부 상황에서는 변수가 선상의 일부 범위에서 이산이고 다른 변수에서는 연속일 수 있습니다.
Reference
Continuous or discrete variable – Wikipedia
상관(dependence)
통계에서 상관(dependence or association)은 두 확률변수(random variables or bivariate data)의 인과에는 무관한 단지 통계적 관계일 뿐입니다. 가장 넓은 의미에서 상관관계(correlation)는 통계적 연관성이지만 일반적으로는 한 쌍의 두 확률변수가 선형적으로 관련되는 정도를 나타냅니다. 상관에 부가되는 인과의 예는 부모와 자녀의 육체적인 체격 사이의 상관관계와 한정적으로 공급되는 제품에 대한 수요와 그 가격 간의 상관관계가 있습니다. 상관관계는 실제로 활용될 수 있는 예측가능한 관계(causal relationship)를 나타내기 때문에 유용합니다. 예를 들어, 발전소는 전기수요와 날씨 간의 상관관계를 기반으로 온화한 날에 적은 전력을 생산할 수 있습니다. 왜냐하면 극단적인 날씨에 사람들이 난방이나 냉방에 더 많은 전기를 사용하기 때문입니다.
일반적으로, 상관관계의 존재는 인과 관계의 존재를 추론하기에 충분하지 않습니다 (즉, 상관관계는 인과 관계를 의미하지 않습니다).
공식적으로, 확률변수가 확률적 독립(probabilistic independence)의 수학적 성질을 만족시키지 않는다면 종속변수입니다.
비공식적인 의미에서 상관관계는 종속성과 동의어입니다. 그러나 기술적인 의미에서 사용될 때, 상관은 평균값들 사이의 관계 중 어떤 몇 가지 특정 유형을 의미합니다. 상관의 정도를 나타내는 $\rho$ 또는 $r$로 표시되는 몇몇 상관계수가 있습니다. 이들 중 가장 널리 사용되는 것은 피어슨 상관계수(Pearson correlation coefficient)로 두 변수 사이의 선형관계를 잘 나타내 줍니다. 물론 한 변수가 다른 변수와 비선형관계일 때도 사용할 수 있습니다. 다른 상관계수는 Pearson 상관관계보다 강하게(robust) 개발되었기 떄문에 비선형 상관관계에서 더 민감합니다. 상호정보(Mutual information)는 두 변수 사이의 상관을 측정하는 데에도 적용될 수 있습니다.
Reference
Correlation and dependence – Wikipedia