이항분포 ?
Binomial distribution ?
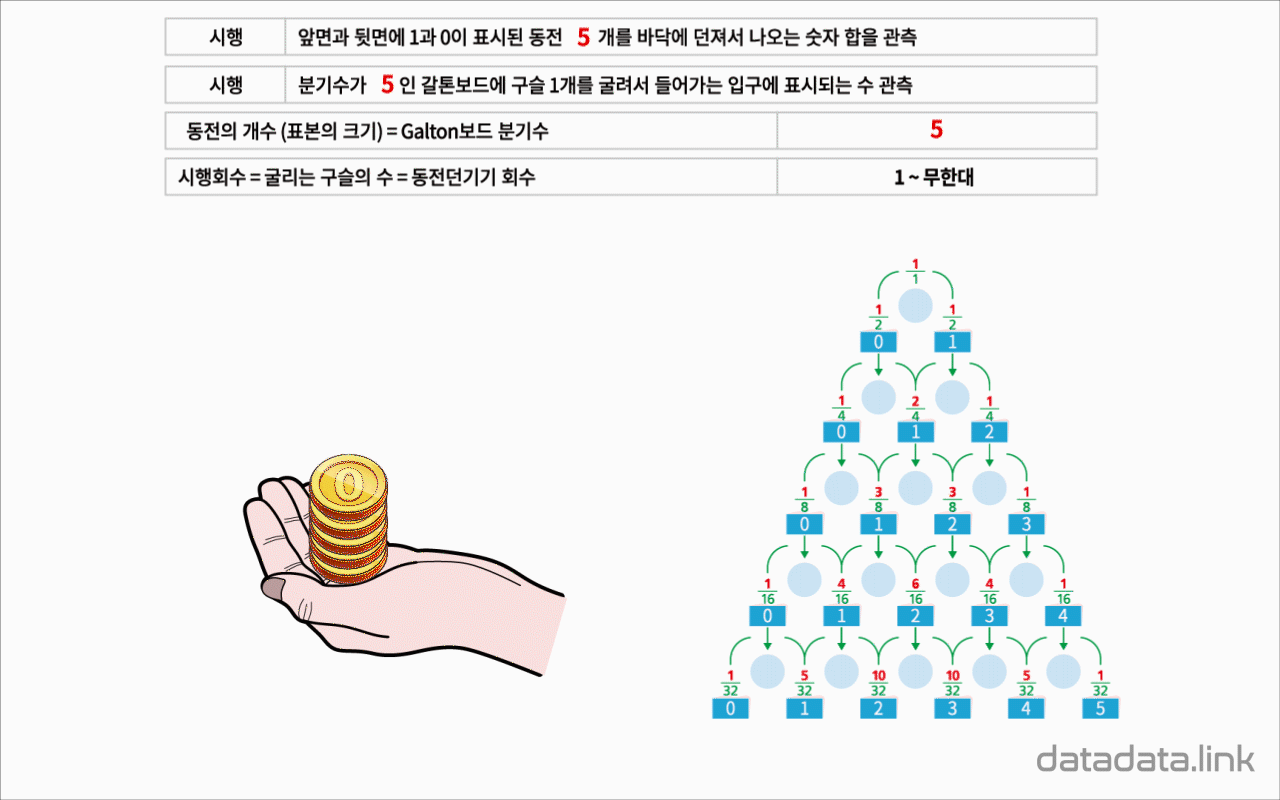
1.1. 동전의 개수(표본의 크기)와 Galton보드 분기수
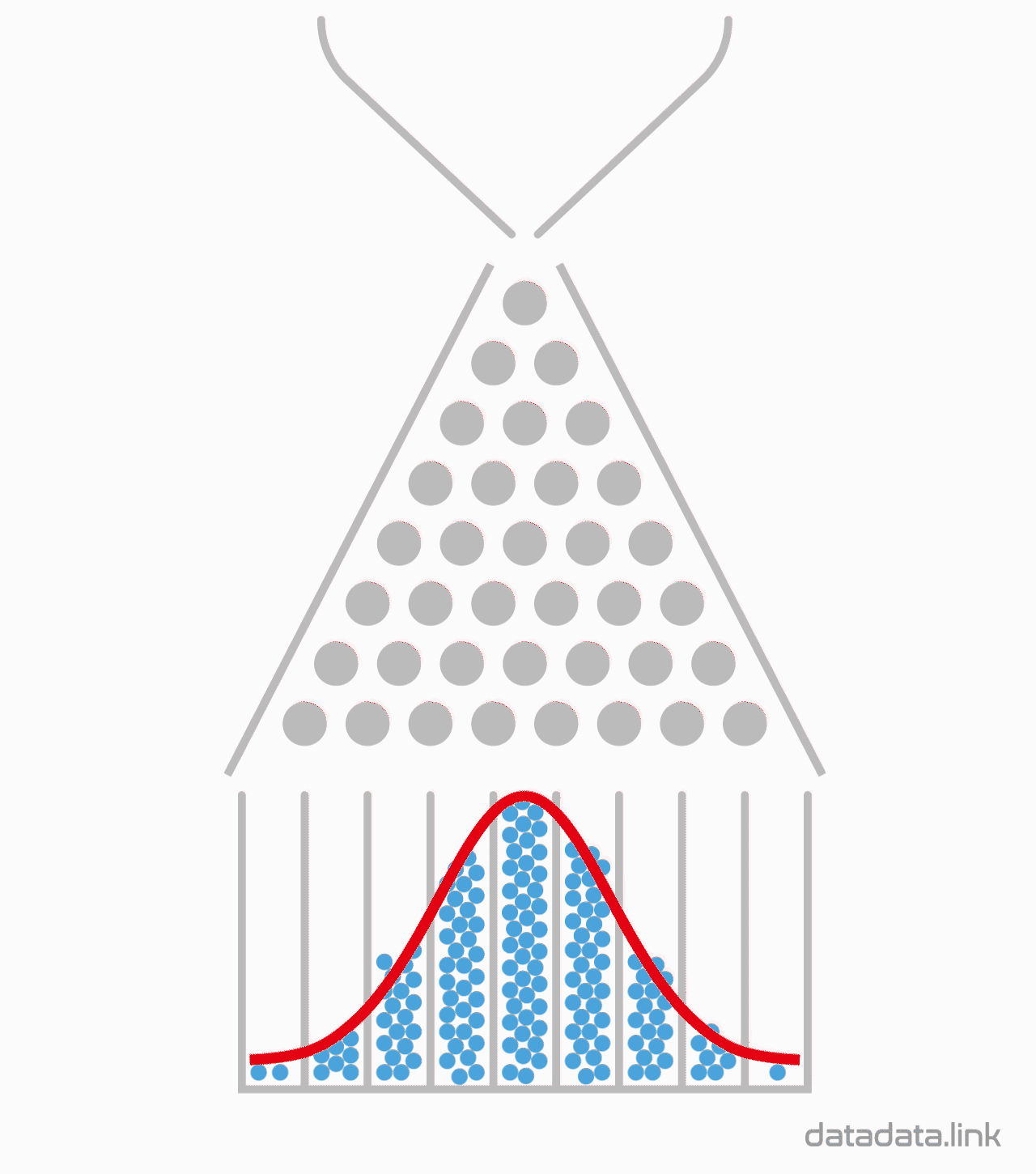
1.2. 8개의 분기수를 가지는 Galton보드에서 많은 수의 구슬을 굴렸을 때 보이는 이항분포 시뮬레이션
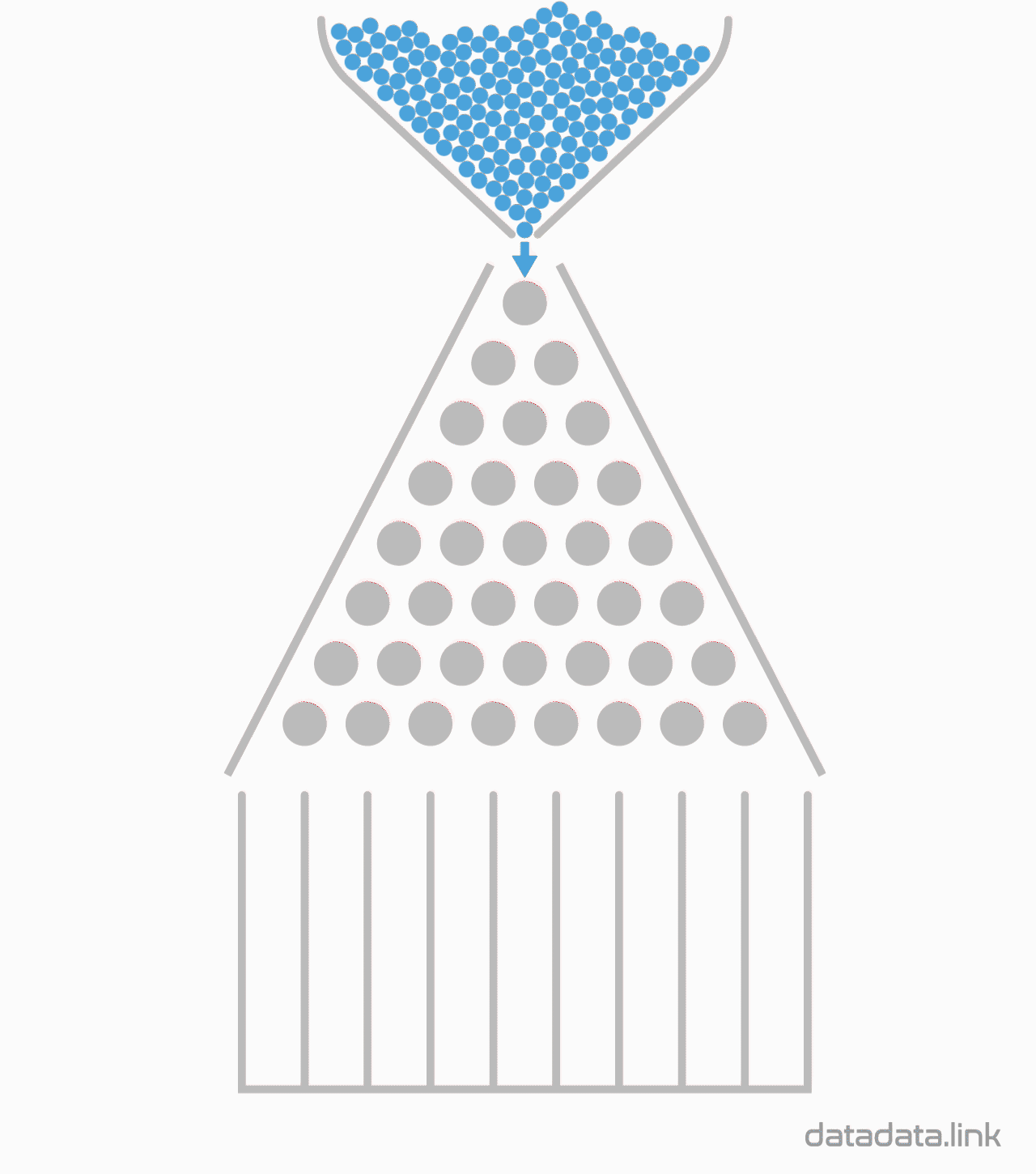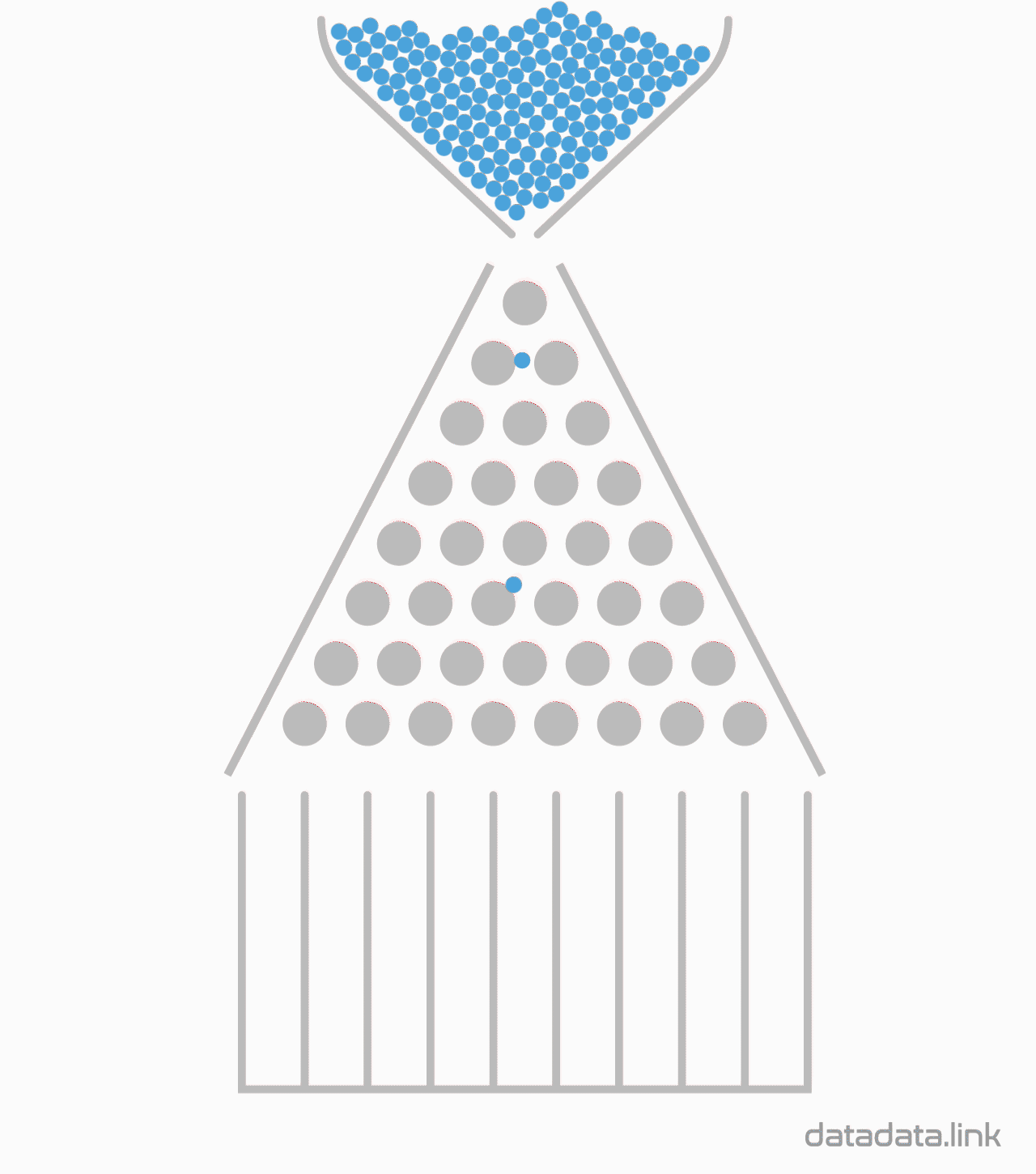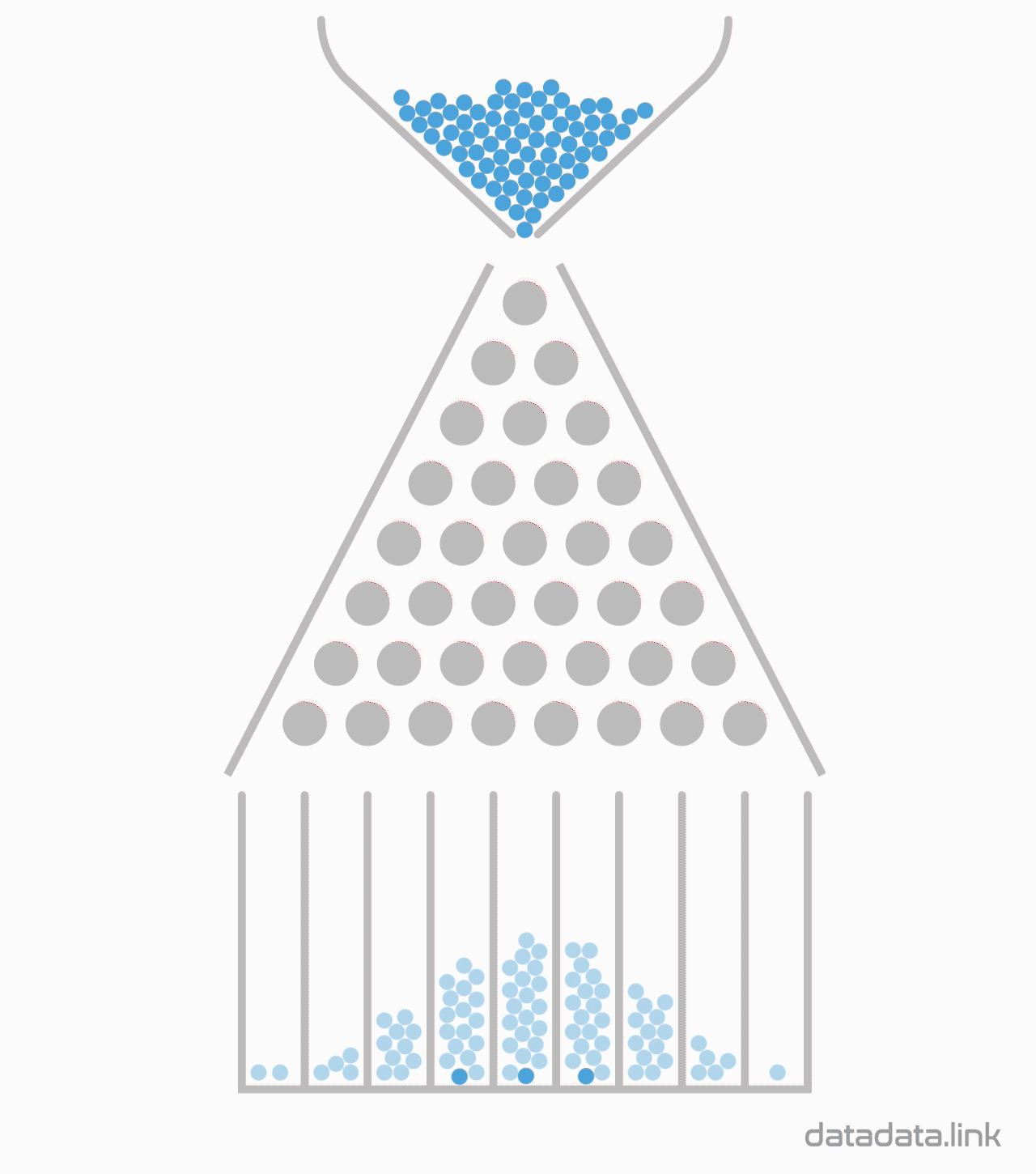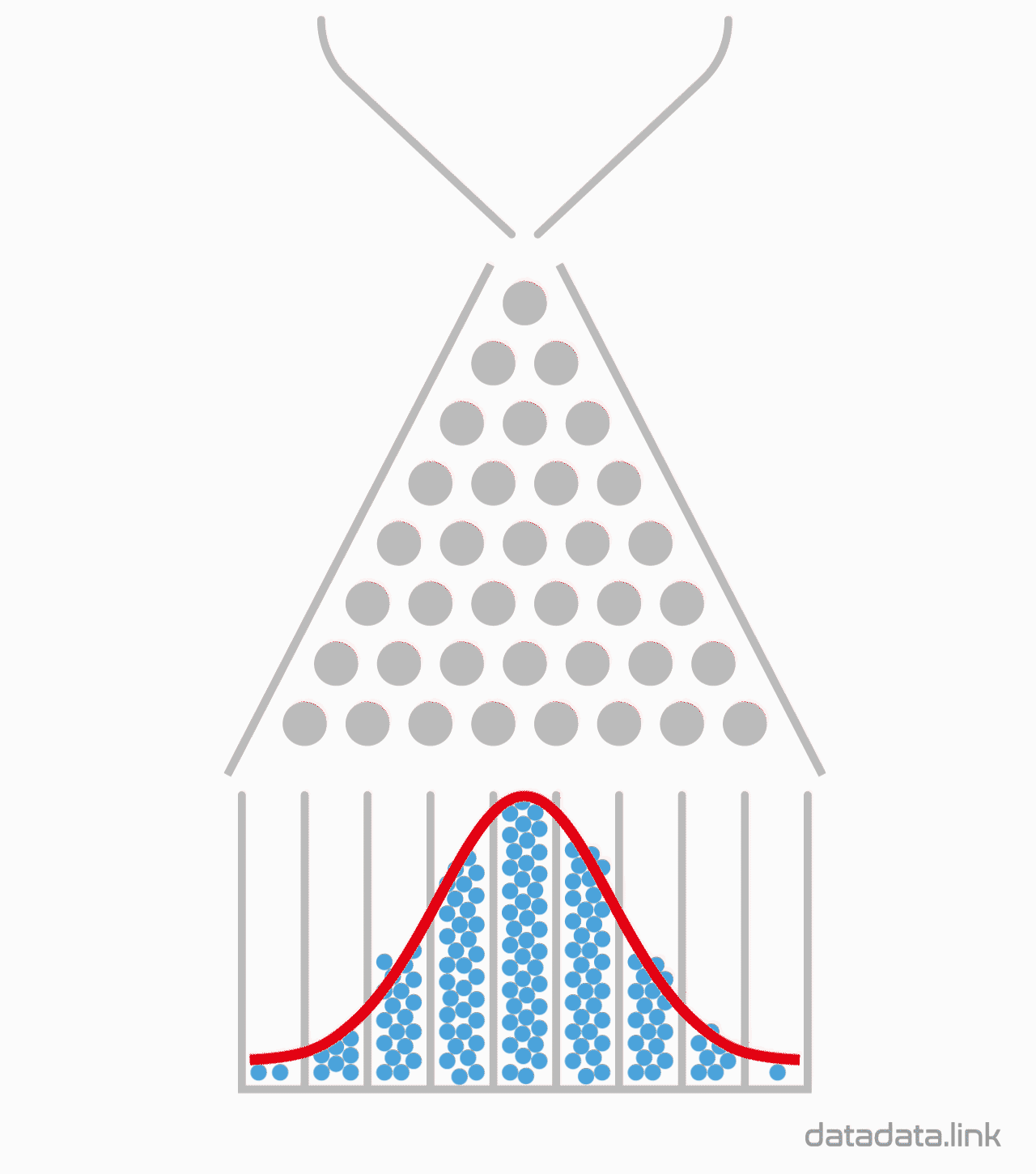
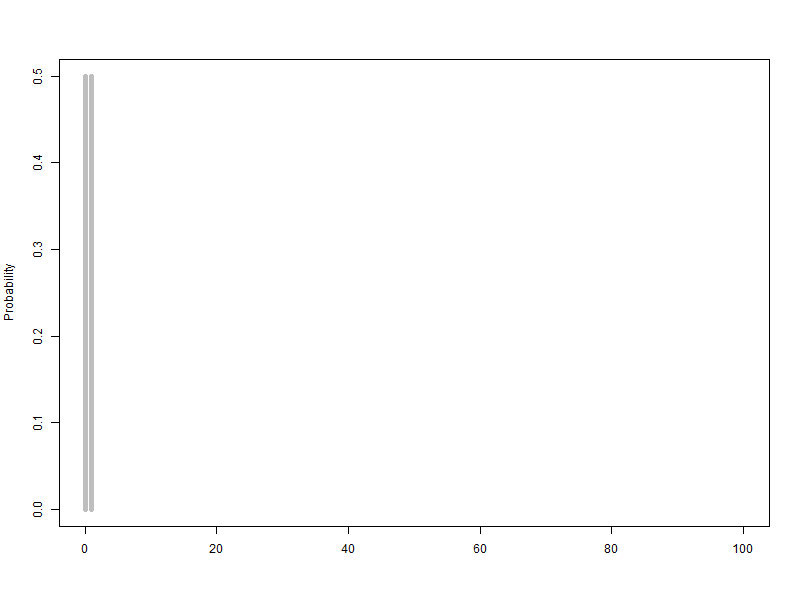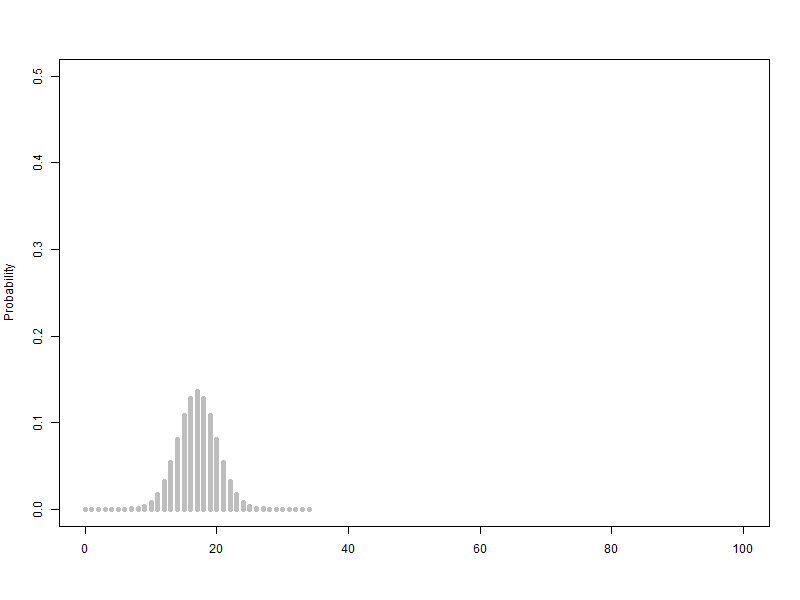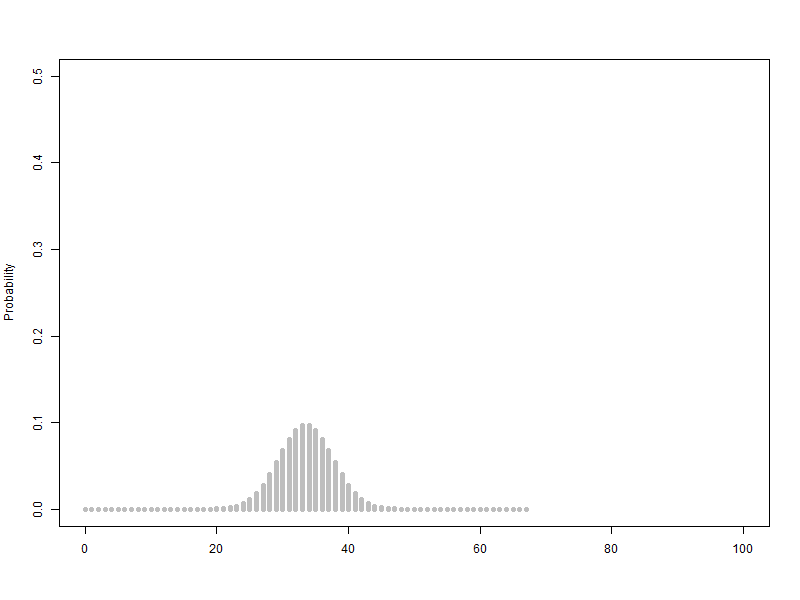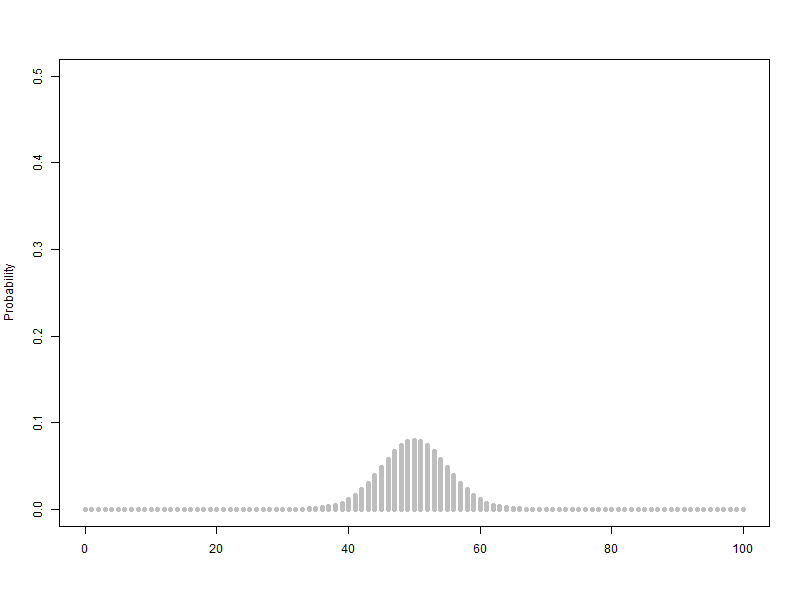
1.3. 10개의 분기수를 가지는 Galton보드에서 많은 수의 구슬을 굴렸을 때 보이는 이항분포 시뮬레이션
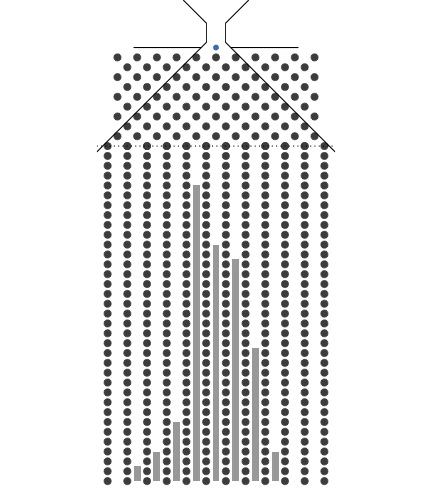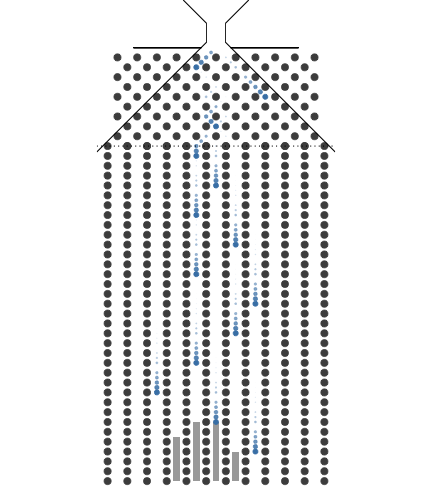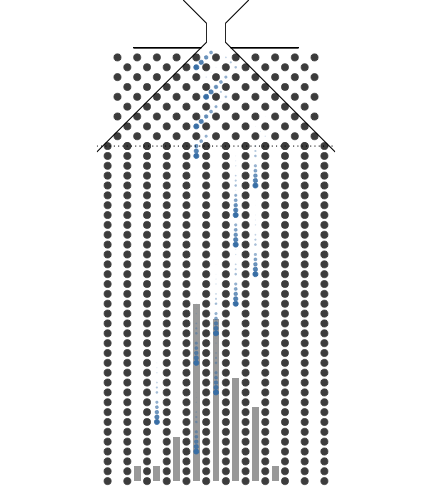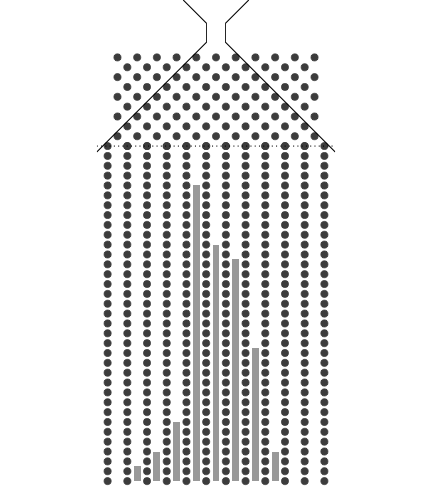
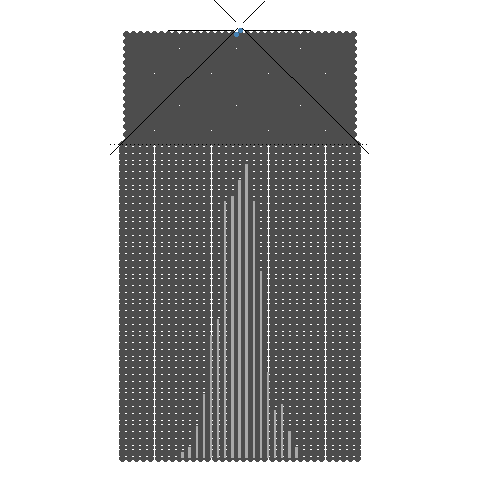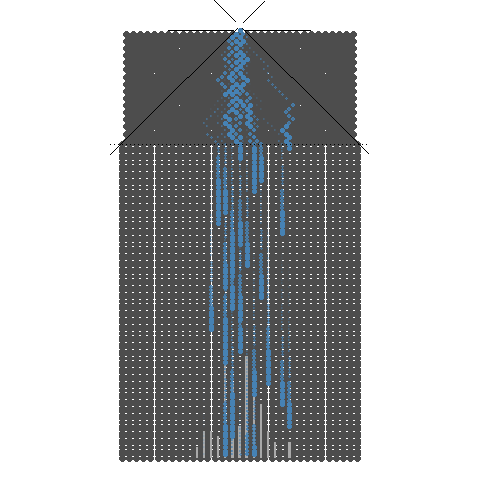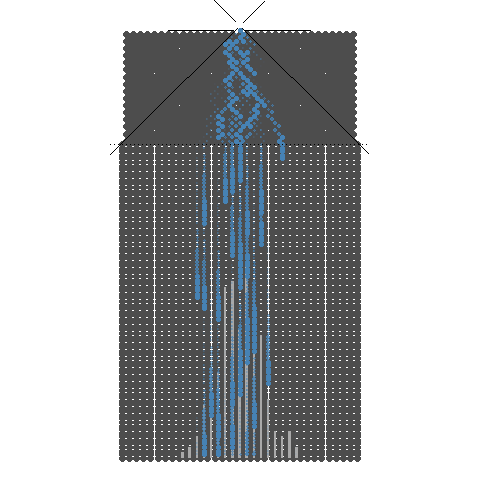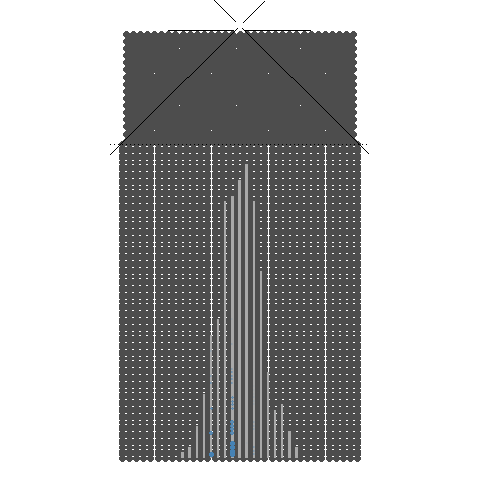
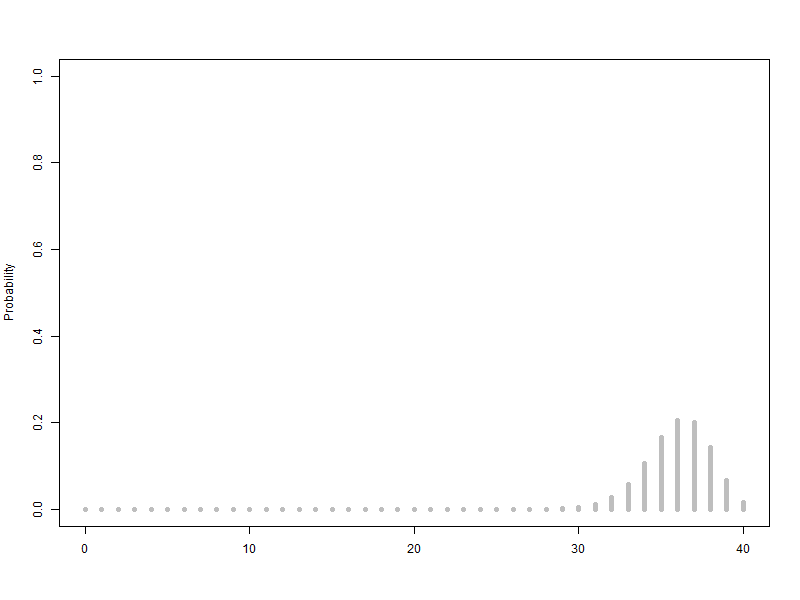
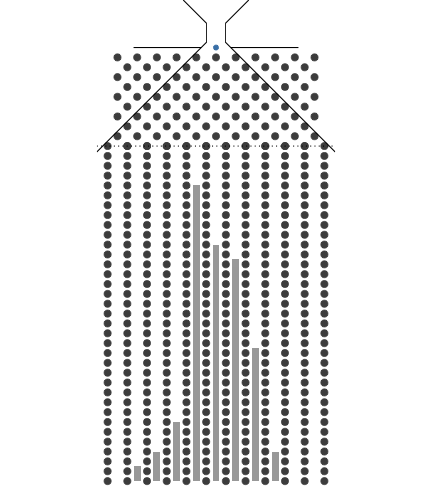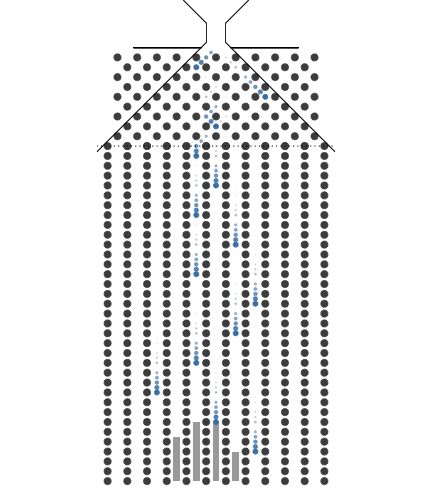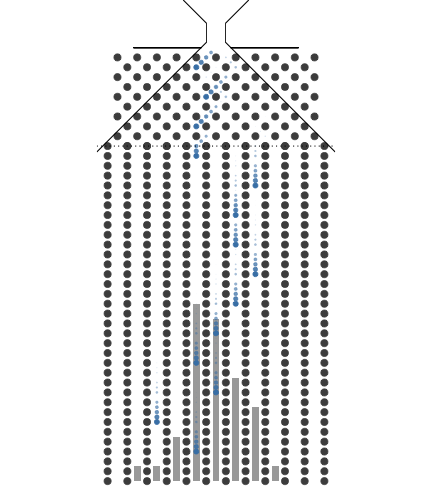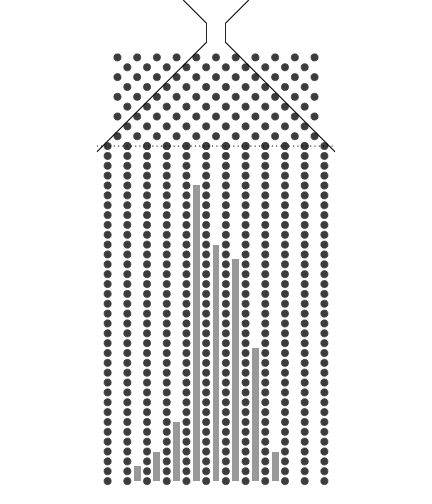
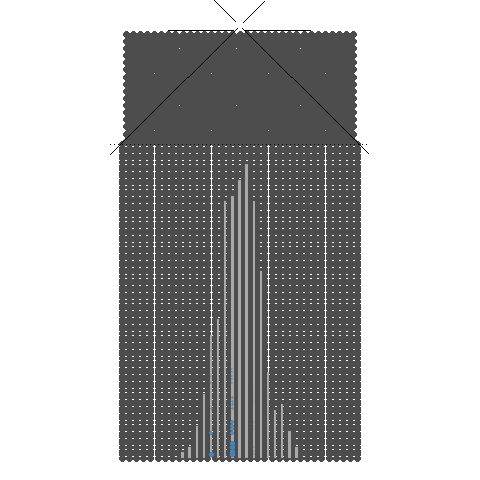
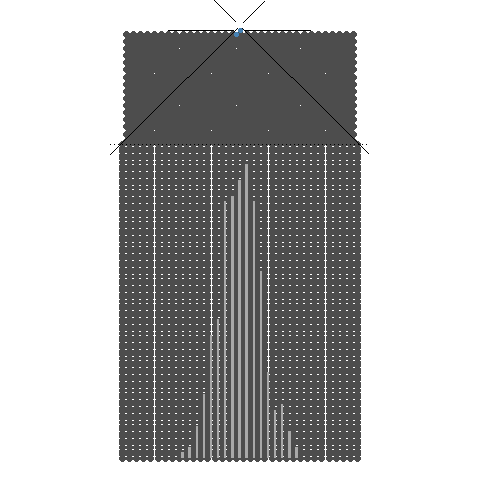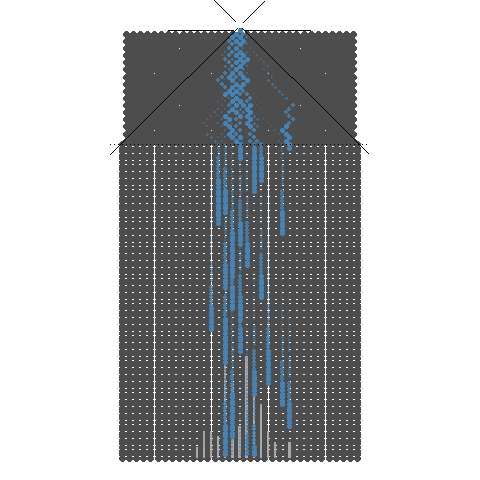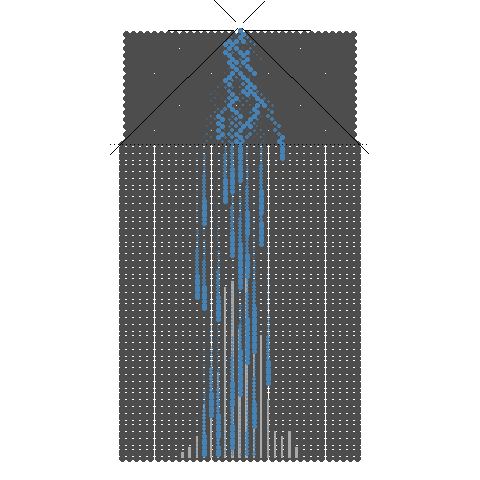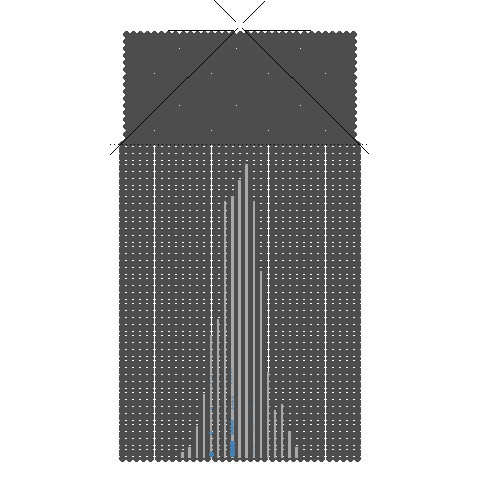
1.4. 32개의 분기수를 가지는 Galton보드에서 많은 수의 구슬을 굴렸을 때 보이는 이항분포 시뮬레이션
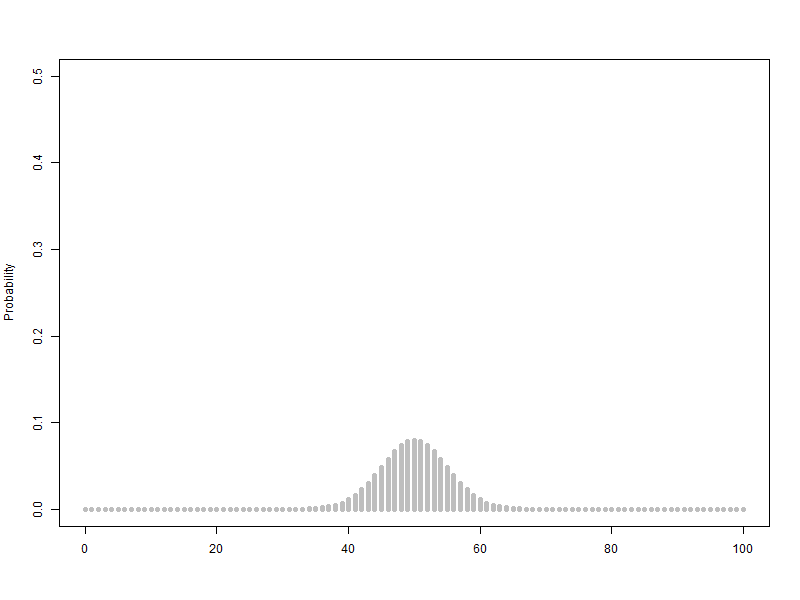
1.5. 베르누이 확률변수를 2개에서 100개까지 늘리는 이항분포(p=0.5) 애니메이션
1.6. 이항분포(p=0.5) : 정해진 구간의 갈톤보드에서 분기수를 1에서 100으로 늘려가는 시뮬레이션
1.7. 이항분포(분기수 n=40)에서 p를 p=0.1에서 0.1씩 늘려가면서 p=0.9까지 시뮬레이션
4.1. 참조
1. 애니메이션
2. 설명
2.1 이항분포
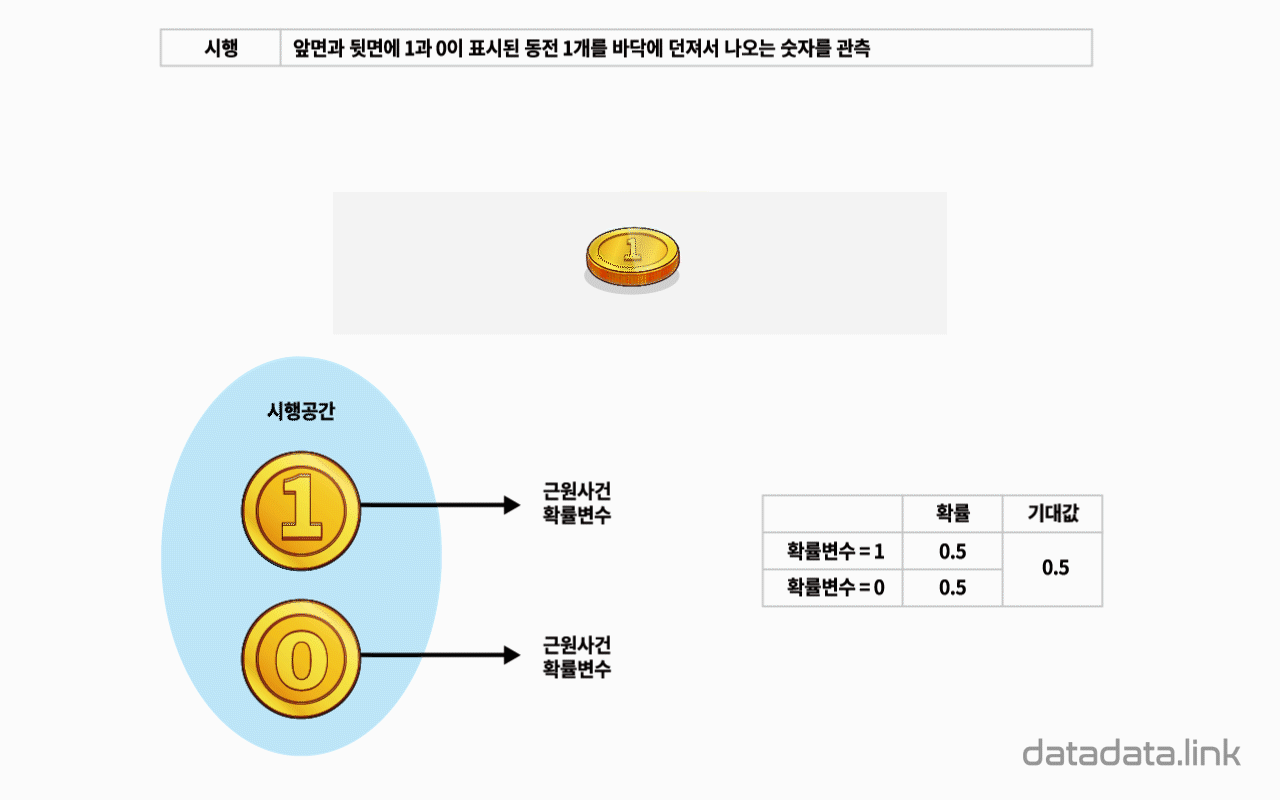
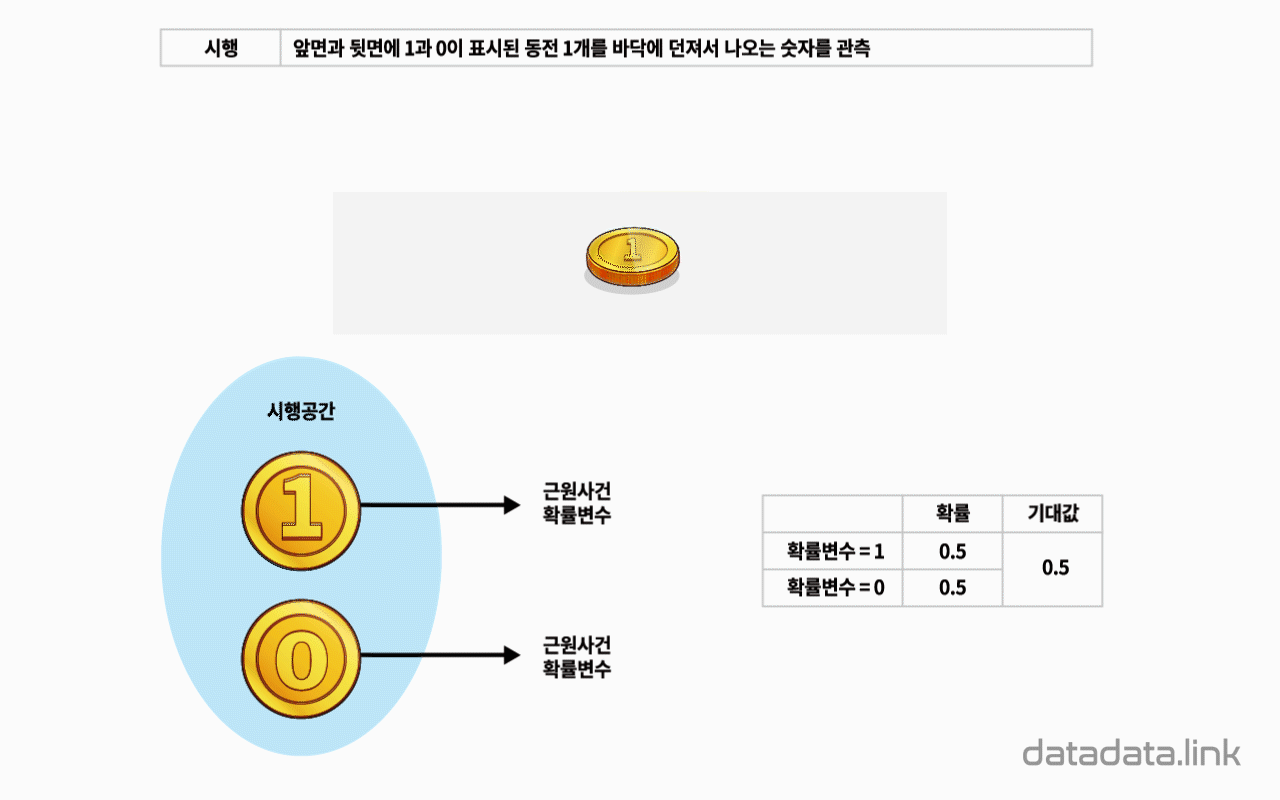
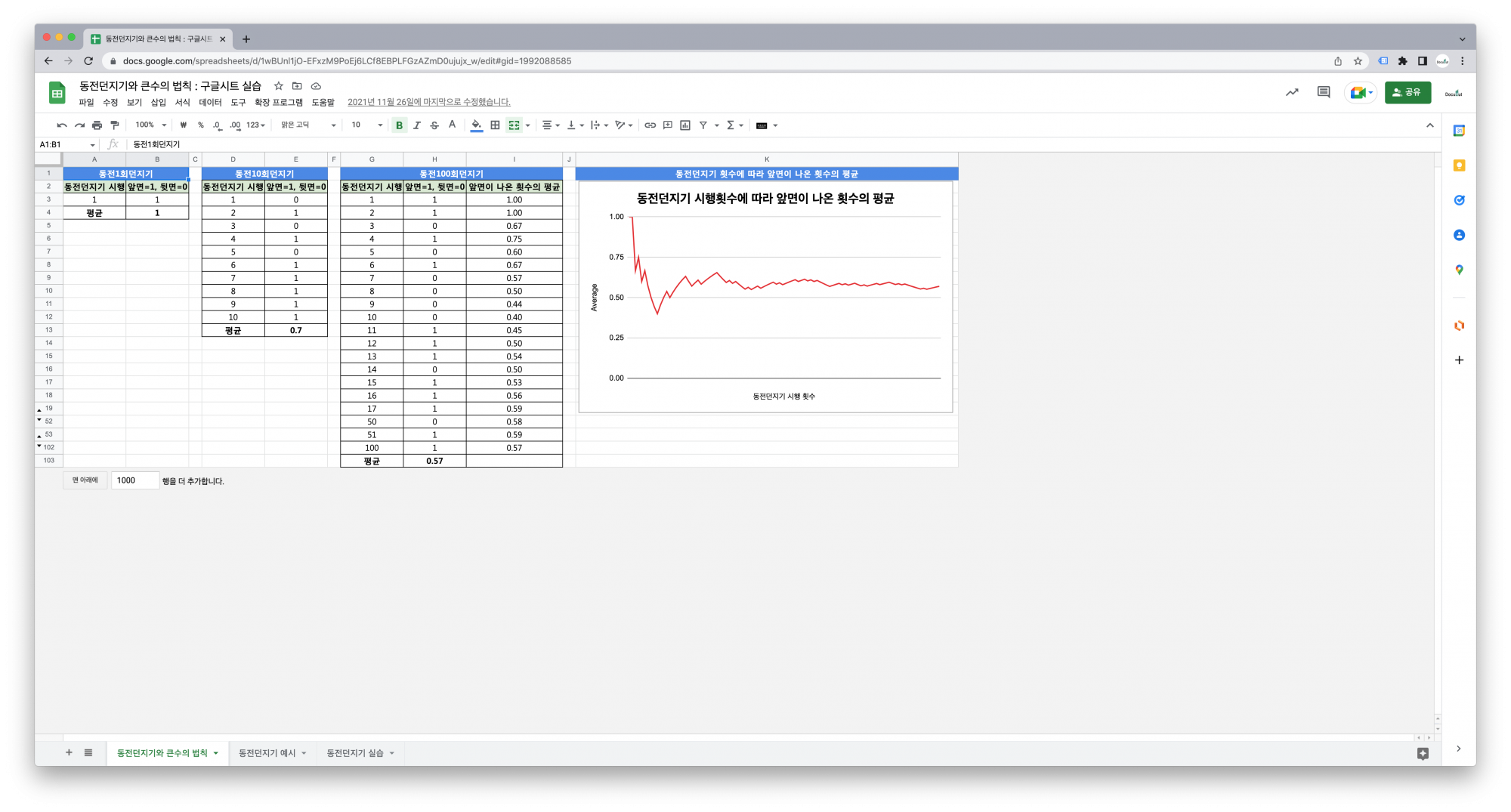
동전 1개를 던져 앞면이 나오는 수를 확률변수라 하면 확률변수는 0과 1이고 2개입니다.
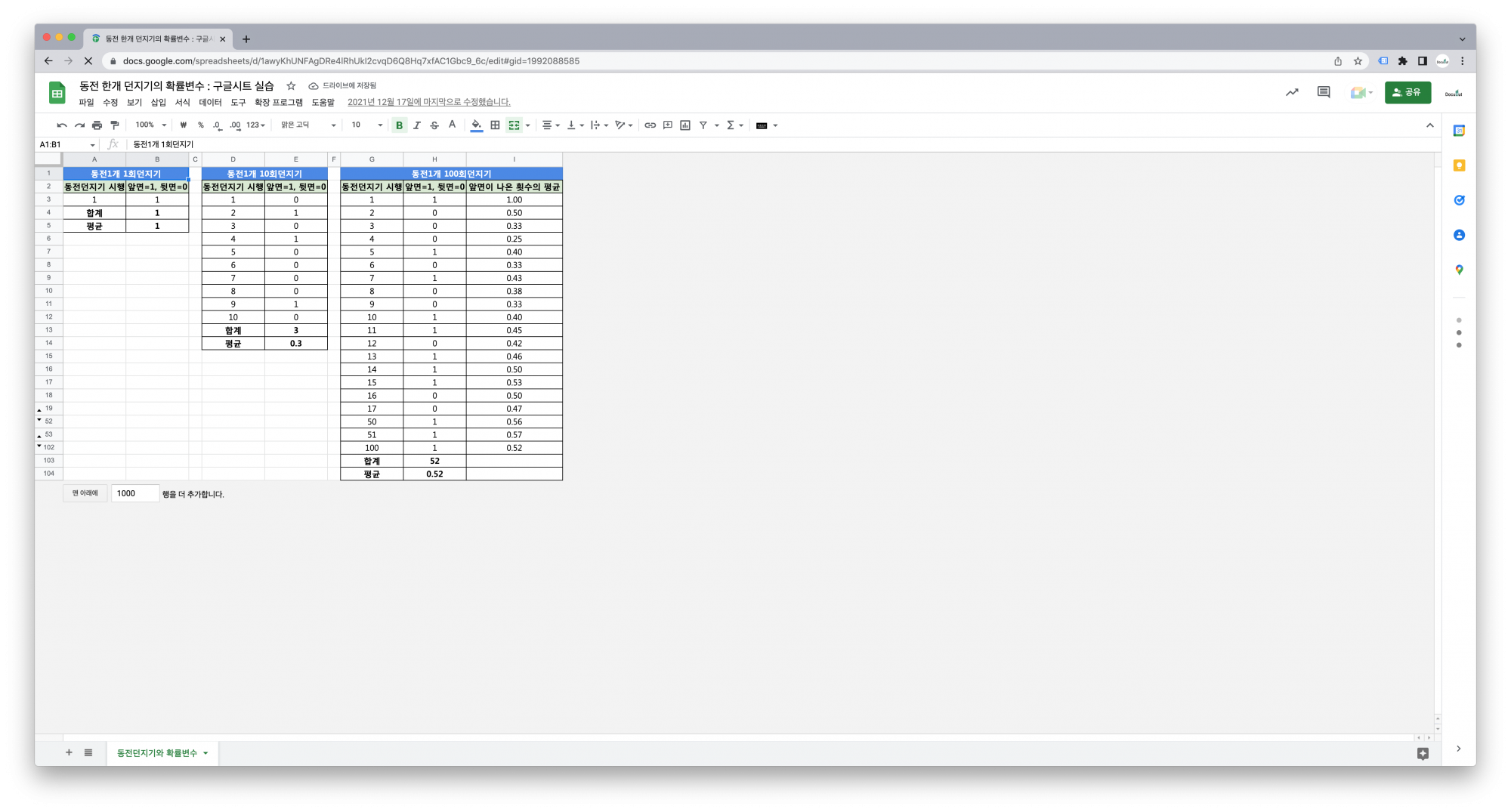
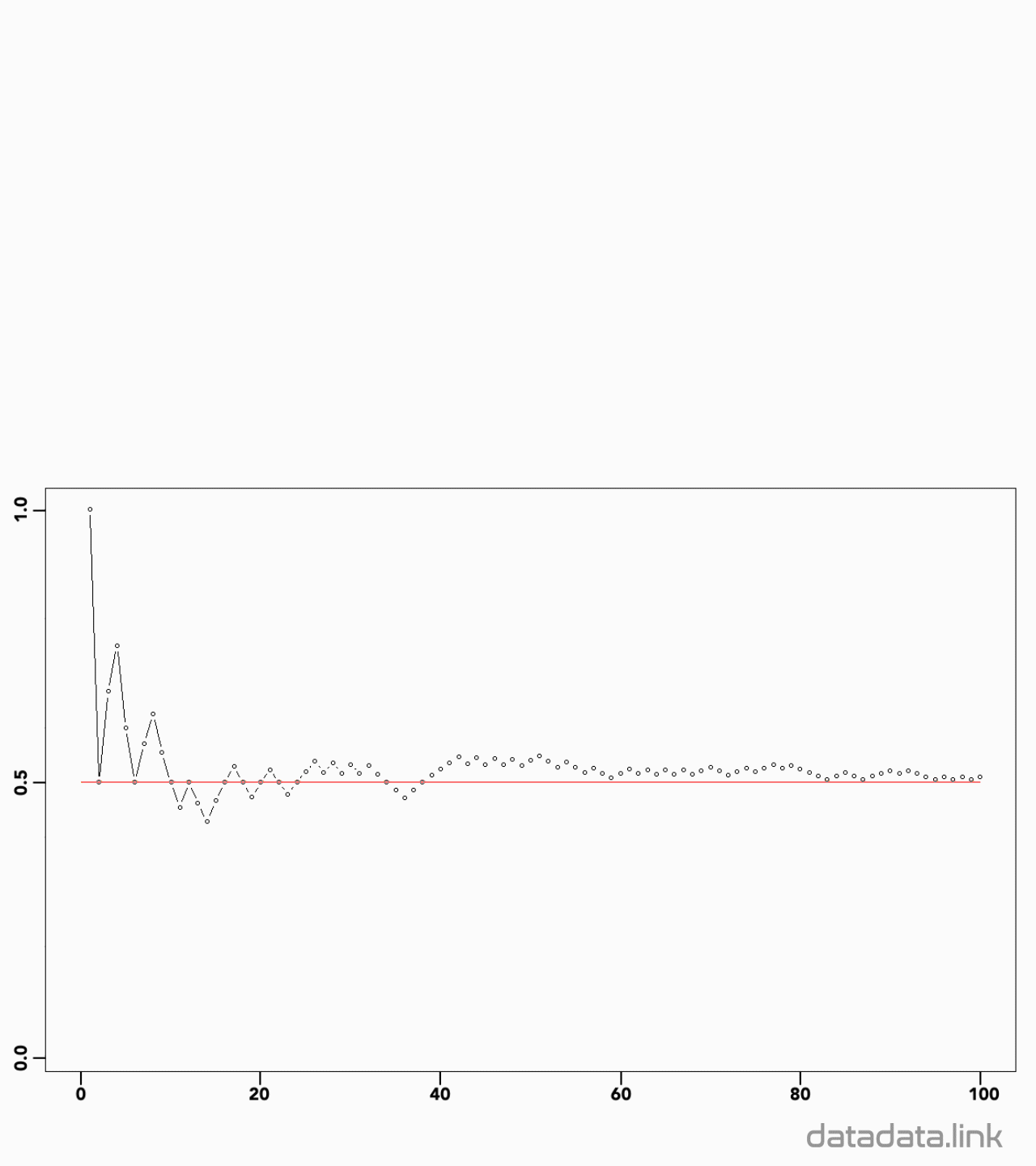
동전을 무한번 던져서 통계학적 확률을 구할 수 있습니다. 이를 큰 수의 법칙이라고 합니다.
완벽한 대칭모양의 동전이라면 동전 1개를 던지는 시행에서 확률변수 0과 1의 확률은 각각 0.5일 것입니다.
동전 2개를 던지면 확률변수는 0, 1, 2로 3개이고 각각의 확률은 0.25, 0.5, 0.25 입니다.
이런 식으로 던지는 동전의 갯수를 하나씩 늘려 확률변수가 2개일 때부터 101개일 때까지 100단계를 하나씩 올려봅니다.
그리고 확률의 분포, 즉, 이항확률분포를 살펴봅니다.
애니메이션에서 보는 것처럼 확률변수의 갯수가 10개 정도까지는 급격하게 확률분포 모양이 변합니다.
하지만 대략 30개가 넘어가면 비슷한 크기의 종모양이 유지되는 모습을 관찰할 수 있습니다.
이 모습은 표본의 크기가 작을 때 t분포를 사용하는 것과 관계가 있습니다.
2.2 이항확률분포(Binomial distribution)
$B\left({n,p}\right)$
$f\left({k;n,p}\right)=\,_{n}\mathrm{C}_{k}\,p^{k}(1-p)^{(n-k)} ={{n!}\over{(n-k)!\,k!}}\,p^{k}(1-p)^{(n-k)}$
$\mathrm{E}\left[{X}\right]=np$
$\mathrm{Var}\left[{X}\right]=np\left({1-p}\right)$
$\mu = p$
$\sigma^{2}={\left({1-p}\right)}^{2}p+{\left({0-p}\right)}^{2}\left({1-p}\right)=p\left({1-p}\right)$
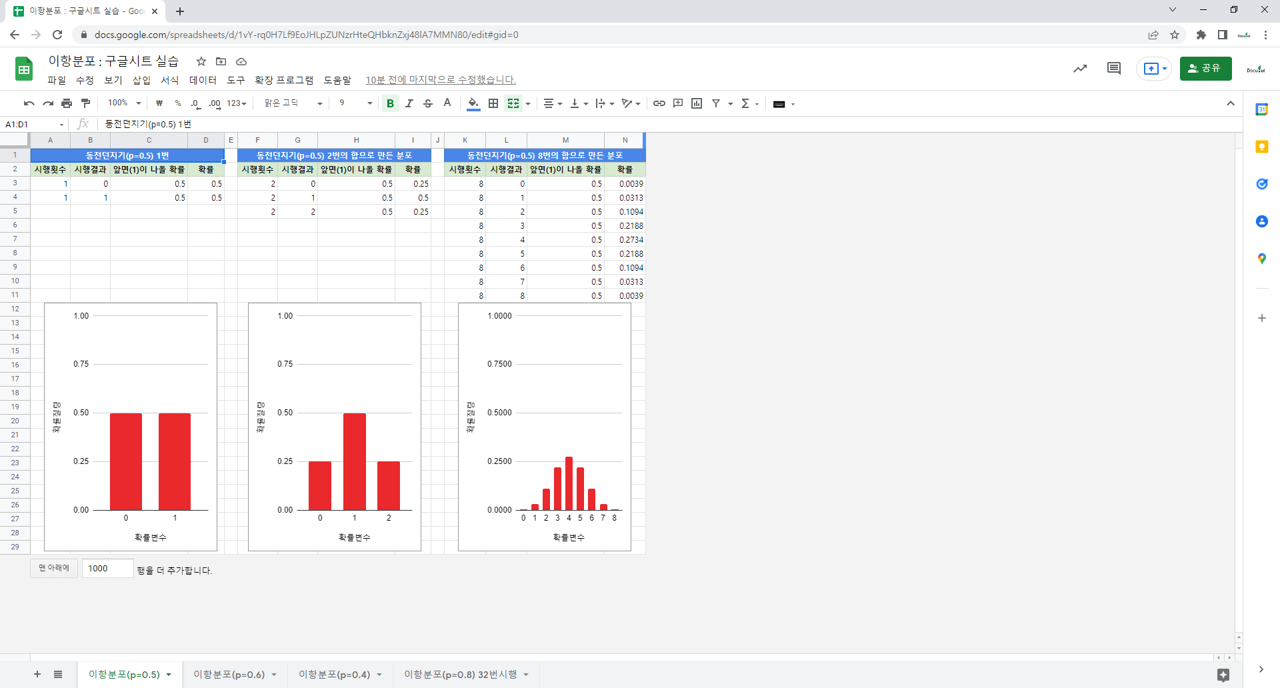
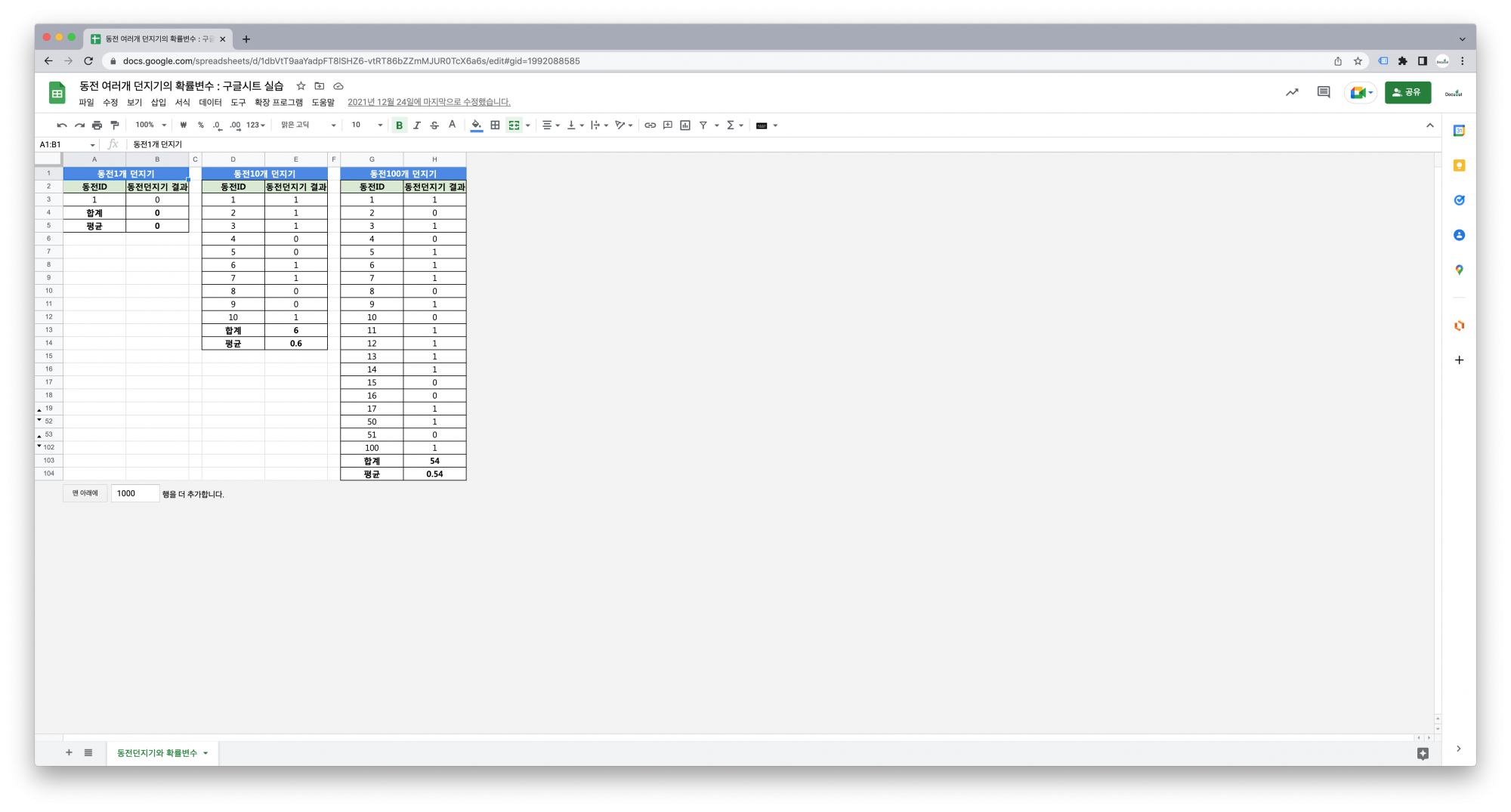
3. 실습
3.2. 함수
=FACT(A3) : 숫자의 계승. A3에 있는 숫자의 계승을 계산함. 예를 들어, A3에 있는 숫자가 2이면, 2×1(2곱하기 1)의 값을 계산해서 표시함. A3에 있는 숫자가 3이면, 3×2×1(3곱하기2곱하기 1)의 값을 계산해서 표시함.
=POWER(C3,B3) : 거듭제곱. C3의 값을 B3의 값만큼 거듭제곱한 값을 계산해서 표시함.
3.3. 실습강의
– 동전던지기
– 동전던지기 결과의 합
– 이항분포